基于遗传算法的战时任务抢修过程优化研究

武子荣，陈曼青，崔伟宁

装甲兵工程学院信息工程系，北京 100072

基于遗传算法的战时任务抢修过程优化研究

武子荣，陈曼青，崔伟宁

装甲兵工程学院信息工程系，北京 100072

目前，我军的很多保障单位在进行战时任务抢修过程的规划时很多都是人工自主决策的，根据之前的情况或经验来进行资源配置和路径选择，最终形成抢修方案，这就存在很大的主观因素，使得决策不科学，方案不合理等。根据上述状况，利用遗传算法来进行任务抢修过程模型的求解，得到抢修过程中的总消耗成本和优化路径，最后代入实例数据取得实验结果。仿真结果表明，基于遗传算法的战时抢修过程优化确实能够得到优化的成本消耗并选出优化路径，得到最优方案。

遗传算法；战时抢修；过程优化

随着仿真技术的不断发展，传统的装备保障模式也受到了这种技术快速发展的影响。仿真技术不但能直观的将整个保障调配过程显示出来，同时能够节省成本，提高效率，易于推广。如果仿真技术与抢修资源优化调度的相关算法有机地结合到一起，并付诸应用，这将大大地提高保障的水平，同时也会大大地提高保障工作的效率，使得战损装备在最短的时间内恢复战斗力，这对装备战斗力的再形成具有较深的影响[1]。

装备抢修工作高效完成是保证装备战斗力的重要因素之一。仿真技术在现代仿真领域的的快速发展并且广发应用于军事中，给战时抢修带来了很好的发展机遇。装备的保障工作为充分发挥、维持、恢复和完善装备作战技术性能的强有力手段，已经成为决定战争胜负的重要因素之一[2]。战时任务抢修过程中指挥决策、资源的配置、调度以及路径的选择等，目前抢修过程基本都是基于人为定制的，因此存在资源配置调度不合理，保障决策不清晰，总体消耗较大等方面的不足[1]。

目前解决这方面的优化问题一般采用智能优化算法进行仿真计算。本文以实际情况为背景，以总体消耗最小为目标，以时间、路程和人员配置以及保障需求量等为基本约束条件，来建立战时任务抢修过程的数学模型。应用改进的自适应遗传算法进行模型的求解[2]。最终得到在总消耗最小的目标下的任务抢修方案。

1 战时抢修过程优化数学模型

在战场环境下，装备抢修过程是一项非常复杂的科目，目前还没有将全部抢修过程按着数学的方法进行模型建立，因为太复杂，根本无法计算，也无法很好的描述建立的模型。因此，为了便于建立模型，也为了便于模型的计算，文章对战时任务抢修过程进行归纳概括，取其核心，概括为资源的调配和路径的选择[3]。

1.1 战时抢修过程优化问题描述

装备抢修过程中包含几个要素，主要有保障单位、物资、抢修分队、待抢修点、行走路径、约束条件和目标条件等。战时抢修过程优化的最终目标。在建立模型前，需要对问题进行一些假设。1）把需要的物资都看成是一种物资；2）保障单位和待抢修点的坐标已知；3）每个待抢修点的物资需求量已知；4）线路的起始和结束位置都在保障单位，每个抢修分队只保障一条线路；5）行驶道路都是通畅的，不考虑交通堵塞等情况。

为了更加接近实际，还应该满足时间的要求，为每个待抢修点增加时间约束，增加最早到达时间和最晚到达时间。假如保障单位派出的抢修分队没能在规定的时间里到达待抢修点，则会给予相应的惩罚[2]。

1.2 模型建立

1.2.1 模型描述

设现有N个需要进行战损任务抢修的单位，保障单位有k个抢修分队，编号分别为（1，2，...K），每个分队能够最多携带的抢修资源量为Q，每个待抢修单位上报的资源需求量为ir（i表示第i个待抢修点，且 Qri≤max）。假设待抢修点i和待抢修点j直接的路径长度为dij，路径长度是通过两点之间的坐标来计算的，如待抢修点i的位置坐标为，待抢修点j的位置坐标为yj )，则求解路径长度的公式为：完成待抢修点i的抢修任务需要的时间为 Ti，且待抢修点i的抢修工作最好在时间窗口[ei，li]内开始，若抢修分队到达待抢修点i的时间早于ei，则分队需在i处等待，如果到达时间晚于 li，则会处以一定的惩罚，产生代价。

一些基本的假设：1）目前暂时设置一个抢修保障单位，所有的抢修分队都是从这里派出，并最后再返回单位；2）每个待抢修点恰好被一个抢修分队进行抢修保障工作，不会交叉抢修；3）每个抢修分队的携带资源量相同；4）每个待抢修点所需的抢修资源量是已知的[4]。

1.2.2 代价函数

违反时间窗所带来的代价应该以合适的方式体现出来，避免在进行抢修方案优化时只考虑资源和路径的优化，而忽略其他的代价。所以用函数的形式来仿真规定的时间窗，这个函数来表示抢修分队违反规定时间段时的代价。原则就是每一个抢修分队偏离规定的时间窗越多，其产生的代价也就越大。根据实际情况，代价的多少可能随着函数曲线增长，本文为了方便计算设置代价随线性曲线增加。

定义的代价函数表达式如下：

上述公式还可以写成统一的表达式：

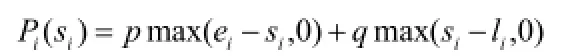
若车辆k在时间窗ei

之前到达待抢修点i，由于统一安排，则分队会等待，产生的代价为；若抢修分队在时间窗li之后到达待抢修点i，则抢修任务被延误，产生延误的代价为；如果抢修分队在时间窗内到达，则代价为0[3]。

1.2.3 目标函数

通过上述的分析说明，以任务抢修时产生的总消耗最小化为目标建立静态模型的目标函数，函数如下：

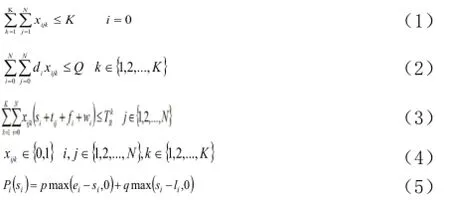
目标函数表示最小化的总消耗成本。包括两项：分队行走路程的消耗成本和所有违反规定时间要求的额外代价消耗。

式（1）表示从保障单位派出抢修分队数不超过K；

式（2）表示所有待抢修点的需求总量不超过抢修分队的总物资量；

式（3）表示分队从待抢修点i到达待抢修点j的时间约束；

式（4）表示整数化的约束，限制只能取0或1；

式（5）表示违反规定时间的额外消耗函数表达式。

1.2.4 参数说明

N：待抢修站点的总数目；

i,j：待抢修点；i，j=（0，l，..，N），i，j=0代表保障单位；

k ：各抢修分队的编号，k=（1，…，K）；

dij：从抢修点i到抢修点j的行走代价，主要是路程，其中i≠j；

α：分队行走单位路程的代价；

Q：抢修分队的最大物资量；

ri：待抢修点i的需求量，且maxdi≤Q；

ei：待抢修点i允许的最早抢修时间；

li：待抢修点i允许的最晚抢修时间；

si：抢修分队k到达待保障点i时的时刻，其中s0=0；

tij：抢修分队从待抢修点i到待抢修点j的时间，其中i≠j；

fi：抢修分队完成待抢修点i的抢修工作所需的时间；

wi：若提前到达待抢修点i则需等待的时间，其中w0=0；

p：分队提前到达待抢修点等待单位时间的代价；

q：分队晚于时间窗到达待保障点的单位时候的代价值。

2 算法设计

2.1 编码解码

编码就是遗传算法用来选择适当问题模型的解的表达方式，由于遗传算法的广泛应用，目前根据不同的问题模型提出了不同的编码格式，使用比较多的有二进制编码、实数或整数编码、字母序列编码等这几种。编码方式的选定取决于实际问题的特点，战时任务抢修过程优化仿真是一种基于次序优化的问题，为了减少无效解的出现，本文采用序号编码。比如派出k个抢修分队，待抢修点为n个，则直接将所有到达的待抢修点以此编码到一条染色体中，这种使用待抢修点序号排列染色体的编码方式比较直观，且保证了每个待抢修点在一次抢修中到达且只到达一次，而且这样的编码格式有利于后期的交叉和变异的操作[4]。

解码是编码的逆过程，即得到编码中的值为满足约束条件的可行解的过程，本文采用的解码类似路径构建的过程，将染色体中的基因值按顺序插入初始化的路径中，如果某一基因在插入时导致路径的一些条件不满足模型中的约束条件，则开始构造新的路径，重复上述操作，直到所有的待抢修点都被插入到路径[4]。

2.2 种群的初始化

种群的规模是会影响优化结果的，当规模较小时，算法的优化性能不太好，而当种群规模较大时，则有较大的时间和空间复杂度。一般对于染色体不大的解设定的种群规模在20-200之间。本文使用随机生成方法初始化种群，由于编码时使用整数编码形式，所以本文采用随机生成种群规模大小的数目来初始化种群。

2.3 适应度函数

适应度函数一般都是非负的，其值越大越好，个体适应度值越大，表示该个体性能越优良，一般是由目标函数变换得到的。由于本文建立的模型是求最小值，所以把目标函数值的倒数作为个体的适应度值，这样函数值越小的个体，适应度值也就越大[5]。

2.4 选择算子

选择算子是从父代中选择优良的个体组成新的种群，进行繁殖得到下一代的操作。选择算子的好坏直接影响了下代种群的优劣，是影响算法优化结果的重要的部分。个体被选中的概率跟其适应度值的大小有关，个体适应度值越大，被选中概率越大。遗传算法选择策略有轮盘赌法、锦标赛法等多种，本文采用的是轮盘赌法，即基于适应度比例的选择策略，个体被选中的概率为，其中Fi为个体i的适应度值；N为种群个体数目。对于父代适应度值本来就很大的个体，可以不经过概率选择，直接用来繁殖下一代，这样能够更进一步的保留种群的优良特性，这就是精英选择策略。将轮盘赌法融入精英选择策略，能够保证最优父代个体顺利进行繁殖，提高算法效率[5]。

2.5 交叉算子

交叉算子是将选择到的两个个体进行部分染色体交换重组，来产生新的个体。由于模型编码采用的是分队序号排列编码，为了适合其编码的格式，交叉方法采用父串部分区域交叉的方法。交叉过程如图1所示。

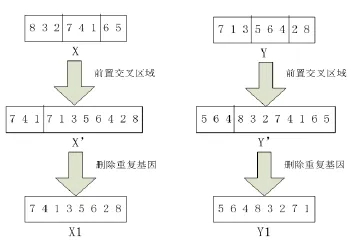
图1 部分区域交叉过程图

2.6 变异算子

本文根据前面部分的设计，采用部分区域倒置法进行变异操作。具体的设计过程是随机选择染色体上的两个变异点，然后将变异点间的基因进行位置倒置，进而得到新的个体[6]。

3 模型求解

以某部实战演练时各部参加战斗时的地理位置和战损抢修时的需求量等为本次仿真优化的原始数据。如表1所示。

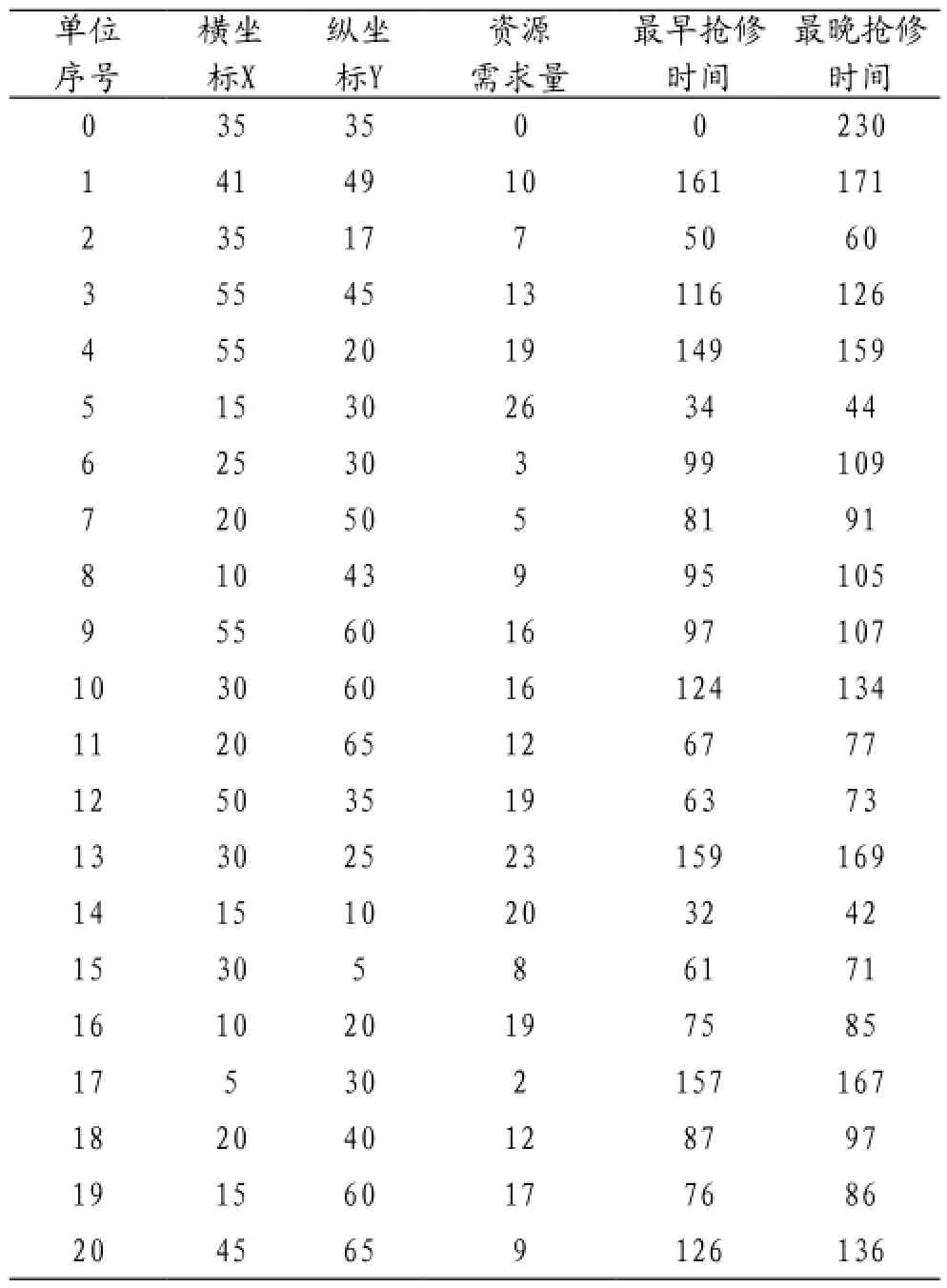
表1 各单位的详细数据

抢修分队行走单位路程的代价为8，抢修分队早到等待的代价0.5，晚到的代价1.5。遗传算法中的各个参数为：种群规模50，交叉概率0.5，变异概率1.5，进化代数为500。

按着上述的实验数据进行模型求解，使用MATLAB进行10次实验，得到最优解为4625.85，分队数为6个，最优解时的进化代数为112代。

实验结果的路线规划图如图2所示。

图2 路线规划图

由图2，可以得出优化的路线，如表2所示。

表2 抢修优化路线

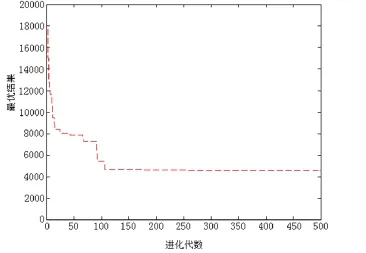
图3 算法收敛情况

图3是算法运行时的迭代优化情况，可见算法收敛的速度比较快，实验数据为112代时收敛到最优解，算法性能较好。

4 结论

本文通过对战时任务抢修的描述，分析了战时抢修的特点，建立了比较符合实际情况的数学模型，设置了必要的约束条件，使得模型更加符合实际，设计了性能较好的遗传算法求解模型得到了较为理想的实验结果，在一定程度上都能辅助决策者制定抢修优化方案。

[1]马懿，卢昱，陈立云，等.战时装备维修保障力量优化调度问题研究[J].计算机工程与应用，2012，8：8-11.

[2]孙宝琛，贾希胜，程中华.战时装备维修保障资源优化模型[J].火力与指挥控制，2013，6：159-162.

[3]王锐，李羚伟，郭波，等.一种基于多目标多约束的战时抢修力量调度[J].兵工自动化，2010，1：34-37.

[4]袁春，郭立滨，雍岐东，等.基于遗传算法的油料装备维修保障资源调度研究[J].物流技术，2011，1：148-150.

[5]王焕坤，刘艺，杨宏伟.改进型遗传算法在战时维修器材配置中的应用[J].四川兵工学报，2011，11：63-66.

[6]袁爽.改进遗传算法的铁路物资应急调度研究与应用[D].兰州交通大学，2014.

Study on the Optimization of Wartime Repair Process Based on Genetic Algorithm

Wu Zirong，Chen Manqing，Cui Weining
Department of Information Engineering, Academy of Armored Forces Engineering ,Beijing,100072

At present, many of our security units are artificial autonomous decision-making in the process of wartime repair, according to the situation or experience to make resource allocation and path selection, and ultimately form a repair program, which has a large subjective factors, and the decision is not scientific, unreasonable and so on. According to the above conditions, using genetic algorithm to carry out tasks repair process model to solve and get the repair process of total cost and optimizing path and the substitution instance data obtained experimental results. The simulation results show that the optimization of the process of the repair process based on genetic algorithm can be optimized and the optimized path can be obtained.

Genetic algorithm; wartime repair; process optimization

TP3

A

1674-6708（2015）145-0124-04

武子荣，硕士研究生，装甲兵工程学院信息工程系，计算机仿真技术

陈曼青，副教授，装甲兵工程学院信息工程系，计算机仿真技术

崔伟宁，讲师，装甲兵工程学院，计算机应用技术