基于边界元法声场辐射预测研究

吕国策

长春职业技术学院，吉林长春 130000

基于边界元法声场辐射预测研究

吕国策

长春职业技术学院，吉林长春 130000

采用边界元法预测结构振动的声场声压，已经得到广泛研究，然而边界积分方程建立的过程中遇到奇异积分，虽然此时也采用高斯积分，但计算收敛性降低。本文针对奇异积分问题采取广义极坐标变换，对比了两种结构网格对边界元法计算结果的影响，结果表明，采用广义极坐标变换后，边界元法可以预测振动辐射声场声压，当频率升高时，某些频率结果误差增加，为此，在提高网格质量后，在低频情况两种结果与解析解极为接近，高频段较好的网格质量度数值计算结果的精度有所提高，但计算时间乘倍增加，不利于工程实际，对于大型问题要综合考虑，在不影响计算精度的同时，可以适当降低网格数量，以降低计算时间。

边界元；奇异积分；广义极坐标变换

由于机械振动产生强烈的噪声，工程中振动产生的噪声越来越受到人们的关注，而噪声对现场工作人员产生极大心理和胜利危害，为解决此问题，各国都相应出台了相应的措施限制现场噪声，机械制造商相应的也对其产生的噪声采取了相应的控制措施。对生产制造商而言，在进行制造前提前预知机械产生的噪声强度对后续工作有指导意义，所以需要一种有效地计算辐射声场声压方法[1-3]。

1 边界元方程的建立

声在介质中传播，假设介质为理想流体，流体不存在粘滞性，没有扰动，宏观上静止，且介质绝热，并且声波是小振幅声波，声压远小于介质静态声压，由以上假设可以将非线性问题转化为线性声辐射问题，而我们关注的多数问题都是脉动振源产生的稳定的简谐声波，所以有声压辐射公式[4-5]

根据理想流体小振幅声波辐射的波动方程，可以得到helmholtz等式。

其中k为波数， /k cω= ，其伴随方程为

伴随方程的基本解为

我们仅考虑辐射声压，所以有B=0，有伴随方程的基本解

利用第二格林公式建立边界积分方程

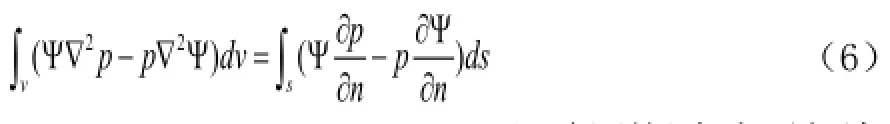
假设基本解和声压满足此方程，得到场点声压与边界信息之间的关系

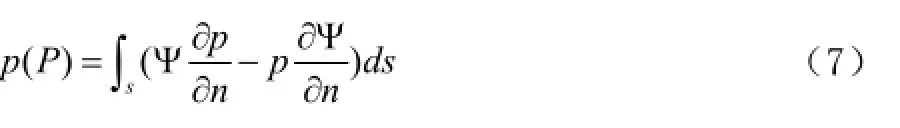
2 边界奇异积分的处理

对于给定的结构，可能仅了解边界表面振动部分信息，然而通过以上边界积分方程可知，要得到场点声压，必须要有所有边界信息，包括表面振动速度和声压，当给定边界条件时，可以将场点p配置到边界表面上，然而基本解这时存在奇异性，对于奇异积分的处理，本文采用极坐标变换法引进雅克比消除奇异积分的方法。

如图1所示，将三角主单元转化为正方形单位单元，由此的到转化关系[6]

由上式带入图坐标点可得

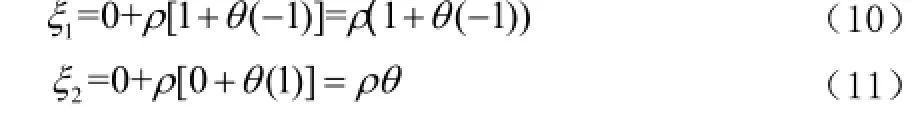
变换后的得到的雅克比

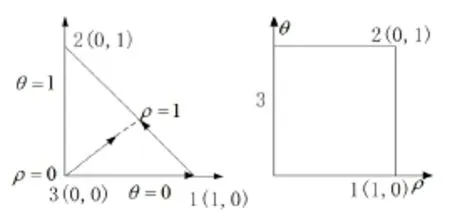
图1 广义极坐标变换

3 脉动求辐射声场验证

脉动球源是指随时间在进行均匀振动的球体，表面做简谐振动，脉动求向它存在的声场辐射声压，满足本文假设条件，辐射声场声压可以通过解析公式计算解析解，作为验证边界元法的一种有效手段，与边界元法计算得到的数值解进行对比，验证边界元法的有效性。

对脉动球半径r0=0.5(m)，介质密度ρ0=1.21kg/m3，脉动求表面振动速度ua=1m/s建两种单元模型，脉动球声场辐射声压解析解计算公式有

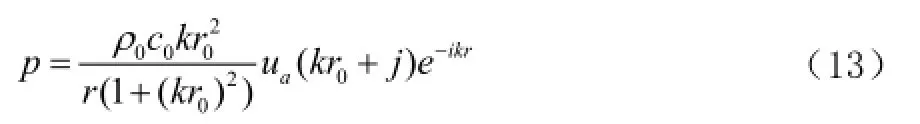
对脉动球边界离散采用四边形网格，选用两种网格尺寸，得到场点网格，第一种为四边形网格单元，单元尺寸为50mm，节点数为1269，单元数为1267，第二种为单元尺寸30mm，节点数和网格数分别为3164、3162，对比网格质量提高后对计算声场声压精度的影响。

由于Fortran语言计算速度较快，适合大型程序开发与维护，针对大型计算问题，可以将模型分配几种情况单独计算，这样可以缩减计算时间，本文边界元积分方程程序采Fortran语言编写。

对于脉动球场声压本文分别计算不同场点和不同频率下声压进行对比，表1为场点网格1对应的不同频率下场点声压解析解和数值解对比结果，从表可以的得出，在低频段，解析解与数值解吻合较好，当频率升高后，数值解相应误差增加。

表2为场点网格2对应解析解与数值解对别结果，与表3变化趋势类似，随频率增加后声压幅值误差有所增加，对比表1，在频率700Hz以上，计算效果明显改善，分析原因由于脉动球建模划分网格质量原因造成表4结果更近解析解。

以上结果分别对比了不同网格不同频率对比结果，表3为网格1计算的到不同场点声压对比结果，频率为50Hz，不同场点得到的声压在低频情况边界元法计算得到的数值结果与解析结果误差较小，并且场点与脉动球源距离变化后误差并没有明显变

表4为在1500Hz频率下计算场点声压结果对比，当频率升高后，场点声压解析解与数值解仍相差较小，误差在1%以下，满足工程应用需要。

对于两种网格，计算时间也有所区别，网格1节点较少，单元较少，而网格2节点数和单元数为网格1的2.5倍，两种网格计算时间分别为277.479 （s）、1568.574（s），网格2的计算时间是1的5.65倍，严重增加了计算时间。

4 结论

场点声压随频率变化数值解与解析解吻合较好，当频率增加声压略微产生波动。场点与脉动球距离变化不大时，声压误差没有明显变化。

网格质量提高后对声场声压预测低频精度没有明显提高，高频误差减小，但计算时间数倍增长。

存在误差可能原因是在离散边界是认为边界单元为平面单元，造成误差。在计算过程中考虑到实际问题不可能将边界离散很多单元，所以本文离散边界单元较大，也造成误差。但这不影响对实际问题的分析。

表1 网格1不同频率对比结果

表2 网格2不同频率对比结果

表3 网格1场点声压结果

表4 网格2场点声压结果

[1]高贵兵，张道兵，岳文辉，等.一种具有唯一解的边界元法计算三维声散射问题[J].机械科学与技术，2013，32（8）：1172-1175.

[2]郭伟，蔡明，马俊.声辐射边界元数值计算[J].船海工程2011，40（1）：101-103.

[3]黎胜，赵德有.用边界元法计算结构振动辐射声场[J]，大连理工大学学报，2000，40（4）：391-394.

[4]杜功焕，朱哲民，龚秀芬.声学基础[M].南京：南京大学出版社.

[5]Ursell F. On the exterior problems of acoustics[C]//Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge University Press， 1973， 74(01): 117-125.

[6] Boundary element acoustics: Fundamentals and computer codes[M]. Wit Pr/Computational Mechanics，2000.

O29

A

1674-6708（2015）145-0113-02