馒头中金黄色葡萄球菌生长预测模型的建立

王亭亭， 曹 慧， 徐 斐*， 袁 敏， 于劲松， 李 洁， 彭少杰， 王李伟

(1.上海理工大学 医疗器械与食品学院，上海 200093；2.上海市食品药品监督所，上海 200233)



馒头中金黄色葡萄球菌生长预测模型的建立

王亭亭1， 曹 慧1， 徐 斐1*， 袁 敏1， 于劲松1， 李 洁2， 彭少杰2， 王李伟2

(1.上海理工大学 医疗器械与食品学院，上海 200093；2.上海市食品药品监督所，上海 200233)

以传统面制品馒头作为研究对象，采用修正的Gompertz(SGompertz)和修正的Logistic(SLogistic)作为一级生长模型，应用Origin 9.0软件分别拟合馒头中金黄色葡萄球菌在10、15、25、30和37 ℃的生长情况，获得其最大比生长速率(μmax)和迟滞期(λ)。采用平方根模型和二次多项式模型建立馒头中金黄色葡萄球菌的二级生长模型，并对该模型进行验证。结果表明，SGompertz模型能较好地拟合馒头中金黄色葡萄球菌的生长。以μmax建立的平方根和二次多项式模型，R2分别为0.931 5和0.932 0，偏差因子(Bf)分别为1.123 2和1.050 1，准确因子(Af)分别为1.221 0和1.190 2，表明采用μmax进行拟合时，二次多项式模型的拟合效果较好；以迟滞期λ建立的平方根和二次多项式模型，R2分别为0.948 4和0.969 6，Bf分别为0.890 1和0.912 2，Af分别为1.541 1和1.180 3，表明采用迟滞期λ进行拟合时，二次多项式模型的拟合效果较好。本研究可为馒头等传统面制品的定量风险评估提供参考。

一级生长模型；二级生长模型；金黄色葡萄球菌；馒头

金黄色葡萄球菌 (Staphylococcusaureus) 隶属于葡萄球菌属(Staphylococcus)，不仅能够引起皮肤感染[1-2]，还容易导致细菌性食物中毒[3-8]。金黄色葡萄球菌的部分菌株可产生致病性肠毒素，该毒素是一种碱性蛋白，在高温下很难消除，可耐受100 ℃煮沸30 min而不被破坏[9-13]，其引起的中毒症状严重。馒头是一类传统面制品，营养丰富，水分活度高，且加工销售条件粗放，极适于金黄色葡萄球菌的生长，馒头中金黄色葡萄球菌不合格的现象时有发生。我国目前已建立的微生物生长预测模型大部分在培养基上完成，无法克服食品基质本身对微生物生长的影响，并且绝大部分只针对肉制品[14-17]、乳制品和蛋类等食品，对馒头这类传统特色面制品的研究较少。因而本研究选用SGompertz和SLogistic作为馒头中金黄色葡萄球菌的一级生长模型，应用Origin 9.0软件分别拟合金黄色葡萄球菌在10、15、25、30和37 ℃的生长数据，并以此获得最大比生长速率(μmax)和迟滞期(λ)。在此基础上，采用平方根模型和二次多项式模型建立馒头中金黄色葡萄球菌的二级生长模型，研究结果可为馒头等传统面制品的定量风险评估提供参考。

1 材料与方法

1.1 材料

1.1.1 菌种来源、培养基及试剂 金黄色葡萄球菌菌株ATCC6538，购自广东省微生物研究所；馒头购自杨浦区的小型食品零售店面；Baird-Parker 琼脂平板、脑心浸出液肉汤(BHI)、亚碲酸钾卵黄增菌液、无菌均质袋,青岛高科园海博生物技术有限公司生产；氯化钠、硫酸钾、硫酸铵、氯化钡、氯化钾(分析纯试剂)，购自国药集团化学试剂有限公司。

1.1.2 仪器与设备 SW-CJ-1FD型洁净工作台，苏净集团苏州安泰空气技术有限公司；YXQ-LS-75SⅡ型立式压力蒸汽灭菌锅，上海博迅实业有限公司；DHG-9203A型电热恒温鼓风干燥箱，上海华连医疗器械有限公司；SCIENTZ-09无菌均质器，宁波新芝生物科技股份有限公司；HWS-150 型恒温恒湿培养箱，上海比朗仪器有限公司；BCD-226K50型冰箱，TCL集团股份有限公司；XW-80A型漩涡混合器，上海精科实业有限公司；FA2204B型电子天平，上海精密科学仪器有限公司。

1.2 方法

1.2.1 样品制备、接种 将金黄色葡萄球菌接种到BHI营养液中，每隔一段时间取出，在600 nm下测吸光值，同时用平板计数法计数，建立吸光值与细菌数量之间的线性关系。当菌种原液浓度至108cfu/mL(OD600=0.15)时，用无菌生理盐水将其梯度稀释至104～105cfu/mL。 每份馒头样品取10 g，将其置于无菌托盘中，在无菌操作台中正反面紫外杀菌各30 min。 取1 mL稀释过的菌液均匀涂抹于杀菌后的馒头上，使初始接种量为103～104cfu/g。将接种后的馒头样品分别置于无菌均质袋中，置于10、15、25、30和37 ℃的恒温培养箱中培养不同的时间。

1.2.2 金黄色葡萄球菌计数及理化指标的测定 到达预设的培养时间后，从培养箱中取出无菌均质袋。将 90 mL无菌生理盐水加入均质袋中，用均质机均质2 min。将均质液梯度稀释后，按照GB4789.10-2010《食品微生物学检验 金黄色葡萄球菌检验》中的平板计数法测定菌落数。

1.2.3 馒头中金黄色葡萄球菌一级生长模型的建立 根据实验得到的馒头中金黄色葡萄球菌在不同温度下的生长数据，选择修正的 Gompertz (a)和修正的 Logistic 模型[18-21](b)为一级模型，用 Origin 9.0 软件拟合馒头在不同温度下的金黄色葡萄球菌的生长数据，根据拟合得到的模型参数，SGompertz模型选用(c)计算出μmax和(d)计算出λ。SLogistic模型选用(e)计算出μmax和(f)计算出λ。

lg(Nt/N0)=a×exp{-exp[-k×(t-xc)]} (a)

lg(Nt/N0)=a/{1+exp[-k×(t-xc)]} (b)

μmax=a×k/e(c)

λ=xc-1/k(d)

μmax=a×k/4 (e)

λ=xc-2/k(f)

式中：Nt、N0分别表示在时间t时和初始时间的微生物的数量(cfu/g)；k为在时间xc的相对生长速率(斜率)；μmax为最大比生长速率(lg(cfu/g)/h)；a为稳定期微生物数量与接种时刻微生物数量的差值；λ为迟滞期(h)；xc为达到相对最大生长速率所需的时间(h)。

1.2.4 馒头中金黄色葡萄球菌二级生长模型的建立 根据一级模型参数计算得到馒头中金黄色葡萄球菌的λ和μmax，利用平方根模型(Square Root model)(g、h)和二次多项式模型[22](Quadratic Polynomial model)(i)分别拟合它们与温度之间的关系，关系式如下：

μmaxorλ=a+bT+cT2(i)

式中：T是实验中的生长温度(℃)；Tmin是理论上金黄色葡萄球菌生长的最低温度；μmax为最大比生长速率(lg(cfu/g)/h)；λ是迟滞期(h)；a、b、c为模型的参数。

1.2.5 模型的可靠性评价 根据相关系数R2，并适当结合残差平方和RSS，可判断一级模型拟合程度的好坏。选择相关系数R2、准确因子Af(k)、偏差因子Bf(j)对二级模型预测效果进行验证和评价[23-24]。一般情况，偏差因子在0.75～1.25之间时，模型可接受；准确因子在1.1～1.9之间时，模型可接受。

式中：observed表示实验实际测得的值；predicted表示根据所得模型预测得到的值；n代表观测值个数(实验次数)。

2 结果与分析

2.1 馒头中金黄色葡萄球菌的一级生长预测模型

采用SGompertz和SLogistic模型，应用Origin 9.0软件分别对金黄色葡萄球菌在5个温度下的生长情况进行拟合(见图1～5)，并由此得到相应的模型拟合参数(见表1)。结果表明，SGompertz模型和SLogistic模型都能较好地拟合馒头中金黄色葡萄球菌在不同温度下的生长状况，SGompertz模型得到的10、15、25、30和37 ℃下的的R2值分别为0.996 8、0.997 8、0.999 1、0.999 1、0.997 0，RSS值分别为0.247 9、0.113 4、0.045 4、0.127 4、0.113 1。SGompertz模型的拟合度较高，且优于SLogistic模型，因此选择其作为金黄色葡萄球菌的最适一级生长模型，并由此计算出最大比生长速率和迟滞期。由表3可见，随着温度的增加，金黄色葡萄球菌在馒头中的最大比生长速率呈上升趋势，而迟滞期呈下降趋势。

图1 SGompertz模型和SLogistic模型拟合的馒头中金黄色葡萄球菌在10 ℃的生长曲线Fig.1 Growth curves of Staphylococcus aureus in steamed bun at 10 ℃ from SGompertz and SLogistic model

图3 SGompertz模型和SLogistic模型拟合的馒头中金黄色葡萄球菌在25 ℃的生长曲线Fig.3 Growth curves of Staphylococcus aureus in steamed bun at 25 ℃ from SGompertz and SLogistic model

图4 SGompertz模型和SLogistic模型拟合的馒头中金黄色葡萄球菌在30 ℃的生长曲线Fig.4 Growth curves of Staphylococcus aureus in steamed bun at 30 ℃ from SGompertz and SLogistic model

图5 SGompertz模型和SLogistic模型拟合的馒头中金黄色葡萄球菌在37 ℃的生长曲线Fig.5 Growth curves of Staphylococcus aureus in steamed bun at 37 ℃ from SGompertz and SLogistic model

表1 馒头中金黄色葡萄球菌的一级生长模型拟合参数

Table 1 The fitting parameters of Primary growth model ofStaphylococcusaureusin the steamed bun

温度/℃模型分类系数axckRSSR210SGompertz4.3958105.54710.01880.13910.9968SLogistic4.2564126.55700.02980.24790.994315SGompertz5.069146.06390.04920.16470.9978SLogistic4.961155.06110.07650.11340.998525SGompertz4.81089.12520.22360.03910.9991SLogistic4.748110.72850.39710.04540.998930SGompertz4.97286.50020.32340.04070.9991SLogistic4.93327.88410.50930.12740.997337SGompertz4.96915.77890.34130.12800.9970SLogistic4.91417.06440.52940.11310.9973

表2 馒头中金黄色葡萄球菌的最适一级生长模型

Table 2 The optimal primary growth model ofStaphylococcusaureusin the steamed bun

温度/℃SGompertz模型方程10lgNt=3.39+4.3958exp{-exp[-0.0188(t-105.5471)]}15lgNt=3.12+5.0691exp{-exp[-0.0492(t-46.0639)]}25lgNt=3.30+4.8108exp{-exp[-0.2236(t-9.1252)]}30lgNt=3.08+4.9728exp{-exp[-0.3234(t-6.5002)]}37lgNt=3.31+4.9691exp{-exp[-0.3413(t-5.7789)]}

表3 SGompertz模型得到的不同温度下的生长参数

Table 3 Kinetic growth parameters estimated by the SGompertz model at different temperatures

温度/℃μmax/lg(cfu/g)/hλ/h100.030452.2989150.091725.7222250.39584.6538300.59163.4079370.62392.8488

2.2 馒头中金黄色葡萄球菌的二级生长预测模型

分别采用平方根和二次多项式模型作为二级模型，应用Origin 9.0软件分别对最大比生长速率、迟滞期与温度的关系进行拟合，结果如图6、7所示。

由图6、7可见，平方根模型和二次多项式模型都能较好地拟合温度与μmax及λ之间的关系。二次多项式模型的拟合结果较优，采用其拟合温度与μmax之间的关系时，R2为0.932 0；采用其拟合温度与λ之间的关系时，R2为0.969 6，因此选择二次多项式模型为金黄色葡萄球菌的最适二级模型。

2.3 模型评价

利用偏差因子Bf和准确因子Af验证模型的可靠度。Bf值在0.75～1.25范围之内，Af在1.1～1.9之间，通常认为该模型可以被接受。Af和Bf值越接近1，模型越可靠。R2则用来评价模型的拟合度，R2越接近1说明预测模型拟合度越好。因此，本研究采用R2、Bf和Af对所建的平方根模型和二次多项式模型进行评价，结果如表4所示。由表4可知，在对馒头中金黄色葡萄球菌生长温度与最大比生长速率μmax之间的关系进行拟合时，平方根模型的Bf为1.123 2，Af为1.221 0，R2为0.931 5，二次多项式模型的Bf为1.050 1，Af为1.190 2，R2为0.932 0，由此可见，二次多项式模型的Bf和Af更接近于1，且R2更接近于1，因此采用μmax进行拟合时二次多项式模型的预测效果较好。

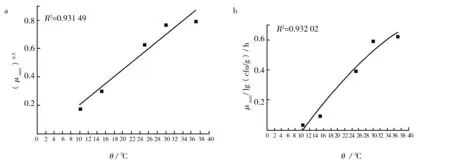
图6 平方根模型(a)和二次多项式模型(b)拟合的馒头中μmax与生长温度的关系曲线Fig.6 Square Root model(a) and Quadratic Polynomial model (b)of the maximum growth rate of Staphylococcus aureus at different temperatures in the steamed bun

图7 平方根模型(a)和二次多项式模型(b)拟合的馒头中λ与生长温度的关系曲线Fig.7 Square Root model(a) and Quadratic Polynomial model (b)of the lag time of Staphylococcus aureus at different temperatures in the steamed bun

生长参数模型类型方程BfAfR2μmax平方根模型μmax=0.0248(T-1.9283)1.12321.22100.9315μmax二次多项式模型μmax=-2.9674×10-4T2+0.0384T-0.36051.05011.19020.9320λ平方根模型1/λ=0.0184(T-2.4365)0.89011.54110.9484λ二次多项式模型λ=0.1112T2-6.9219T+108.17690.91221.18020.9696

在对馒头中金黄色葡萄球菌生长温度与迟滞期λ之间的关系进行拟合时，平方根模型的Bf为0.890 1，Af为1.541 1，R2为0.948 4，二次多项式模型的Bf为0.912 2，Af为1.180 2，R2为0.969 6，由此可见二次多项式模型的Bf和Af更接近于1，且R2更接近于1，因此采用λ进行拟合时二次多项式模型的预测效果较好。

3 讨 论

SGompertz模型能较好地拟合馒头中金黄色葡萄球菌在不同温度(10、15、25、30和37 ℃)下的生长，其R2值都在0.99以上，RSS值均小于0.37，因此选择SGompertz模型为金黄色葡萄球菌的一级生长预测模型。在对金黄色葡萄球菌生长温度与其最大比生长速率之间的关系进行拟合时，二次多项式模型的Bf为1.050 1，Af为1.190 2，R2为0.932 0，均接近于1，因此选择二次多项式模型预测馒头中金黄色葡萄球菌在不同温度下的最大比生长速率，对应的二次多项式模型为μmax=-2.967 4×10-4T2+0.038 4T-0.360 5。在对金黄色葡萄球菌生长温度与其迟滞期之间的关系进行拟合时，二次多项式模型的Bf为0.912 2，Af为1.180 2，R2为0.969 6，因此选择二次多项式模型预测馒头中金黄色葡萄球菌在不同温度下的生长迟滞期，相应的二次多项式模型为λ=0.111 2T2-6.921 9T+108.176 9。本研究可为馒头等传统面制品的定量风险评估提供参考。

[1] Isabel CM Fensterseife，Osmar N Silva，Uru Malik，et al．Effects of cyclotides against cutaneous infections caused byStaphylococcusaureus[J]．Peptides，2015，63：38-42．

[2] Effat Abbasi Montazeri，Azar Dokht Khosravi，Abbas Jolodar，et al．Identification of methicillin-resistantStaphylococcusaureus(MRSA) strains isolated from burn patients by multiplex PCR[J]．Burns，2015，41(3)：590-594．

[3] 许振伟，韩奕奕，孟瑾，等．熟食肉制品中金黄色葡萄球菌风险评估基础研究[J]．包装与食品器械，2012，30(5)：40-41．

[4] Tara C Smith，Shylo E Wardyn．Human Infections withStaphylococcusaureusCC398[J]．Current Environmental Health Reports，2015，2(1)：41-51．

[5] Guanghui Li，Congming Wu，Xin Wang，et al．Prevalence and characterization of methicillin susceptibleStaphylococcusaureusST398 isolates from retail foods[J]．International Journal of Food Microbiology，2015，196：94-97．

[6] P DiCiccio，A Vergara，A R Festino，et al．Biofilm formation byStaphylococcusaureuson food contact surfaces: Relationship with temperature and cell surface hydrophobicity[J]．Food Control，2015，50：930-936．

[7] Nielsen LH，Jensen-Fangel S，Benfield T，et al．Risk and prognosis ofStaphylococcusaureusbacteremia among individuals with and without end-stage renal disease: a Danish, population-based cohort study[J]．BMC Infect Dis，2015，15(1)：6．

[8] Brittany L Fries，Carmelo Licitra，Antonio Crespo，et al．Infectious Diseases Consultation and the Management ofStaphylococcusaureusBacteremia[J]．Clinical Infectious Diseases，2014，58(4)：598-599．

[9] Balaban N， Rasooly A． Staphylococcal enterotoxins review[J]．International Journal of Food Microbiology， 2000，61(1)：1-10．

[10]V Carfora，A Caprioli，N Marri，et al．Enterotoxin genes, enterotoxin production, and methicillin resistance inStaphylococcusaureusisolated from milk and dairy products in Central Italy[J]．International Dairy Journal，2015，42：12-15．

[11]Sakai F，Ihara H，Aoyama K，et al．Characteristics of enterotoxin H-producingStaphylococcusaureusisolated from clinical cases and properties of the enterotoxin productivity[J]．Journal of food protection，2008，71(9)：1855-1860．

[12]Jing Hui，Yan Cao，Fang Xiao，et al．Staphylococcusaureusenterotoxin C2 mutants: biological activity assay in vitro[J]．Journal of Industrial Microbiology and Biotechnology，2008，35(9)：975-980．

[14]龙文玲，姚开，贾冬英，等．肉制品预测微生物模型的研究进展[J]．食品科技，2007，2007(6)：27-30．

[15]刘超群，王宏勋，侯温甫．低温肉制品微生物控制与预测模型应用研究进展[J]．食品科学，2009，30(21)：481-484．

[16]李苗云，田璐，赵改名，等．肉品微生物生长预测模型研究进展[J]．肉类研究，2012，26(12)：20-24．

[17]李飞燕，梁荣蓉，罗欣，等．冷却肉中微生物生长模型和货架期预测模型的研究进展[J]．食品科学，2009，30(z1)：172-177．

[18]Alejandra Tomac，Rodolfo Horacio Mascheroni，María Isabel Yeannes．Modelling the effect of gamma irradiation on the inactivation and growth kinetics of psychrotrophic bacteria in squid rings during refrigerated storage. Shelf-life predictions[J]．Journal of Food Engineering，2013，117(2)：211-216．

[19]Sagdic，Osman．Kinetic Modeling ofEscherichiacoliO157:H7 Growth in Rainbow Trout Fillets as Affected by Oregano and Thyme Essential Oils and Different Packing Treatments[J]．International Journal of Food Properties，2014，17(2)：371-385．

[20]Liang Shen，Zhongtao An，Qingbiao Li，et al．Three-stage fermentation and kinetic modeling of bioflocculant byCorynebacteriumglutamicum[J]．Chinese Journal of Chemical Engineering，2015，23(1)：219-226．

[21]Ting Fang，Lihan Huang．Growth and survival kinetics ofListeriamonocytogenesin cooked egg whites[J]．Food Control，2014，36(1)：191-198．

[22]Z Hamidi-Esfahani，S A Shojaosadati，A Rinzema．Modelling of simultaneous effect of moisture and temperature onA.nigergrowth in solid-state fermentation[J]．Biochemical Engineering Journal，2004，21(3)：265-272．

[23]Ross T．Indices for performance evaluation of predictive model in food microbiology[J]． Journal of Applied Microbiology，1996，81(5)：501-508．

[24]Te-Giffel M C， Zwietering M H．Validation of predictive models describing the growth ofListeriamonocytogenes[J]． International Journal of Food Microbiology，1999， 46(2)： 135-149．

Establishment of Growth Model ofStaphylococcusaureusin Steamed Buns

WANG Ting-ting1, CAO Hui1, XU Fei1, YUAN Min1, YU Jin-song1,LI Jie2, PENG Shao-jie2, WANG Li-wei2

(1.Schl.ofMed.Instrum't&FoodEngin.,ShanghaiUni.ofSci. &Engin.,Shanghai200093;2.Inst.ofFood&DrugInspect.,Shanghai200233)

Traditional flour product of steamed bun was chosen as the object of study. Using the revised Gompertz (SGompertz) and revised Logistic (Slogistic) as a primary growth model to describe growth ofStaphylococcusaureusin steamed buns at different temperatures. In order to obtain the maximum specific growth rate (μmax) and lag phase (λ), Origin 9.0 software was used to fit the growth curve ofS.aureuswith variable storage temperatures (10 ℃, 15 ℃, 25 ℃, 30 ℃, and 37 ℃) and the square root model combine with quadratic polynomial model was used as a secondary growth model ofS.aureusand then the model was verified. The results showed that, SGompertz model can well fit the growth ofS.aureusin steamed buns. Theμmaxand λ values obtained from the SGompertz model were used to establish the secondary growth models. When μmaxwas used as an argument to establish the square root models and quadratic polynomial models respectively,R2values were 0.931 5 and 0.932 0 respectively;Bf1.123 2 and 1.050 1 respectively;Af1.221 0 and 1.190 2 respectively; suggested the quadratic polynomial model could better be employed to predictμmax. When λ was used as an argument to establish the square root models and quadratic polynomial models respectively,R2values were 0.948 4 and 0.969 6 respectively;Bf0.890 1 and 0.912 2 respectively;Af1.541 1 and 1.180 2 respectively; suggested the quadratic polynomial model could better be employed to predict λ. This study can provide theoretical basis for quantitative risk assessment in steamed buns and other traditional flour products.

primary growth model; secondary growth model;Staphylococcusaureus; steamed buns

上海市科委重点攻关项目(13391901400-3)

王亭亭 女，硕士研究生。研究方向为食品安全风险评估。E-mail：wang151ting@163.com

* 通讯作者。女，博士，教授，博士生导师。研究方向为食品安全风险评估。E-mail：xufei.first@263.net

2015-07-08；

2015-08-22

Q939.97;TS201.3

A

1005-7021(2015)06-0049-07

10.3969/j.issn.1005-7021.2015.06.009