一种改进的分数时延估计方法及应用*

2015-12-26柏业超张兴敢

数据采集与处理 2015年6期

关键词：混响环境噪声麦克风

刘超柏业超张兴敢

(1.南京大学电子科学与工程学院，南京，210023；2.东南大学毫米波国家重点实验室，南京，210096)

一种改进的分数时延估计方法及应用*

刘超1,2柏业超1,2张兴敢1,2

(1.南京大学电子科学与工程学院，南京，210023；2.东南大学毫米波国家重点实验室，南京，210096)

传统的分数时延估计算法对环境噪声和混响噪声比较敏感，在复杂的实际环境中，算法性能会严重下降。为进一步提高时延估计算法性能，提出一种基于广义互相关(Generalized cross correlation,GCC)改进算法的广义互相关-最大似然相位补偿(GCC-Maximum likelihood phase compensation,GCC-MLP)分数延时估计算法。该算法改进了GCC频域加权函数，并将线性相位补偿应用于频域互相关谱，获得连续的分数时延估计值，进一步提高了分数时延估计的精确性。仿真结果表明，GCC-MLP相位补偿分数时延估计算法增强了对环境噪声和混响噪声的鲁棒性，减小了时延估计误差，算法性能优于曲线拟合、Sinc插值等传统分数时延估计算法。

广义互相关;分数时延估计；麦克风阵列；声源方向角估计；相位补偿

引言

基于麦克风阵列的声源定位技术在视频会议、语音识别以及可视/车载电话等领域具有广阔的应用前景[1-3]。时延估计是麦克风阵列声源角度估计和声源定位算法中最常用、也是最重要的一种方法[4-5]。分数时延估计通常分为两个阶段。第1阶段利用广义互相关(Generalized cross correlation,GCC)算法进行整数延时单元估计。文献[6]中，根据不同频域加权函数，提出了广义互相关-相位变换(Phase transform，PATH)、广义互相关-最大似然(Maximum likelihood，ML)等一系列算法。第2阶段进行分数延时单元估计。文献[7]提出了曲线拟合分数延时估计算法，这种算法实现简单，但分数时延估计误差比较大。文献[8]采用sinc插值的分数时延估计算法，延时估计精度高，但是该算法受混响噪声的影响较大。本文提出一种基于GCC改进算法的GCC-MLP相位补偿分数延时估计算法。该算法改进GCC算法频域加权函数，增强算法对于环境噪声和混响噪声的鲁棒性；同时，将线性相位补偿和抛物线拟合应用于频域互相关谱，获得连续的分数时延估计值，进一步提高了分数时延估计的精确性，减小了声源角度估计误差。

1 麦克风阵列信号模型

麦克风阵列信号模型的平面示意图如图1所示。假设两麦克风Mic1,Mic2间距为d(约为5 cm)，麦克风阵列中心为O，声源偏离麦克风阵轴线夹角为θ(0°～180°)。在实际环境中，两麦克风接受到的信号x1(t)和x2(t)表示为

(1)

(2)

式中：s(t)为声源信号，h1(t)和h2(t)是房间混响的冲激响应，“*”表示信号卷积，n1(t)和n2(t)为环境噪声，τ1和τ2是声波从声源到麦克风的传播时间。

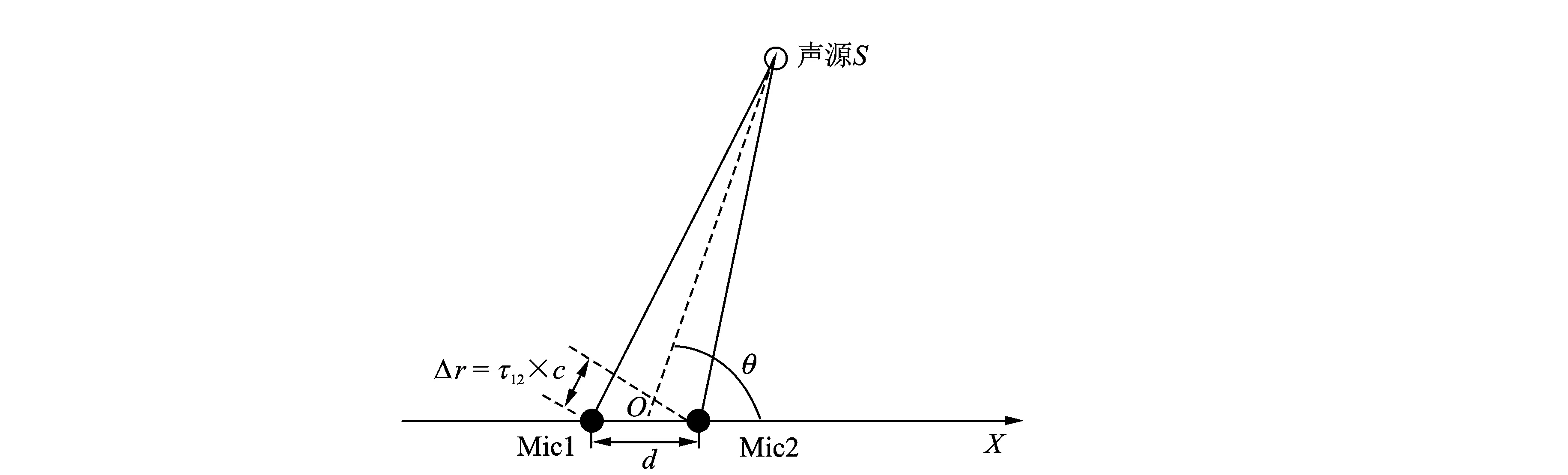
图1 麦克风阵列平面示意图Fig．1 Schematic plan of dual microphone array

由于两麦克风间距为d很小，声源位于麦克风阵列的远场，由几何关系可得声源位置的方向角

(3)

式中：τ12=τ1-τ2,即两麦克风接收信号间的时延，c为声速。由式(3)可知，估计得到τ12便可确定声源位置的方向角θ。

2 GCC-MLP相位补偿分数时延估计算法

2.1 GCC时延估计算法

传统GCC时延估计算法流程图如图2所示。时延估计τ12可以表示为

(4)

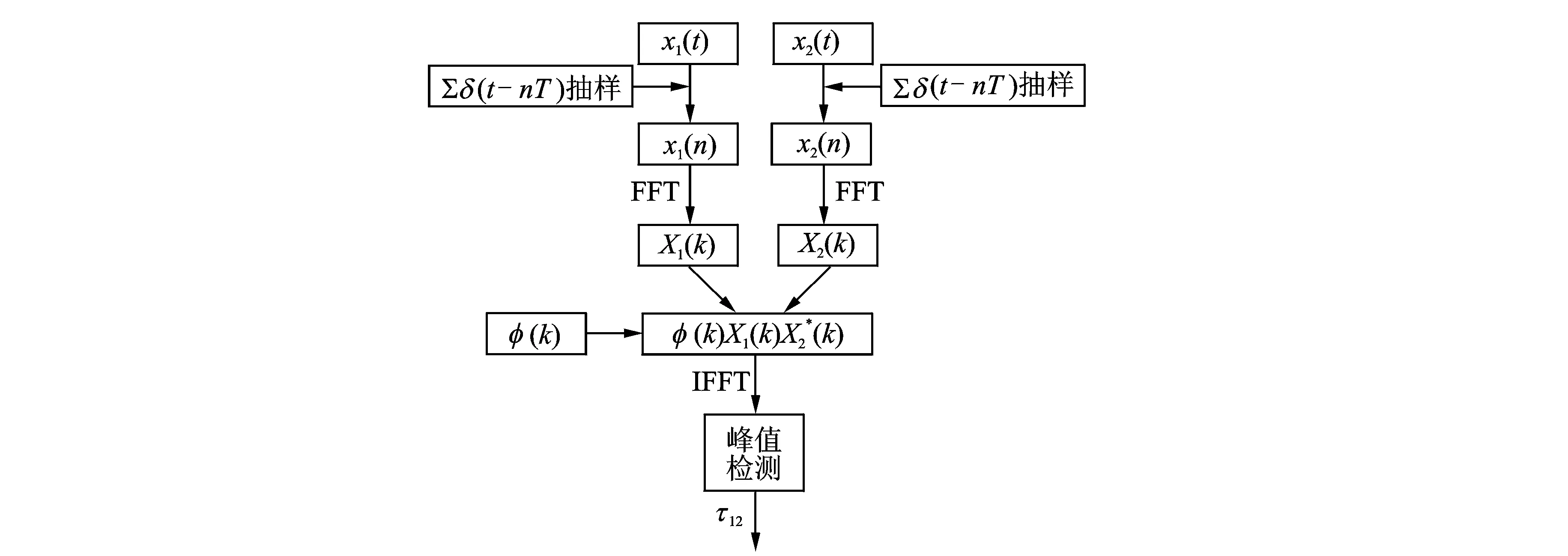
图2 GCC算法流程图Fig．2 Flowchart of GCC algorithm

由式(1,2)可以看出，在时延估计系统中存在两种噪声：环境噪声ni(t)和混响噪声hi(t)*s(t)。选择合适的加权函数对于提高时延估计的算法性能有重要意义。文献[6]研究表明，GCC-ML加权函数对于环境噪声鲁棒性较强，而GCC-PATH加权函数对于混响噪声有较强抑制作用，两种算法的加权函数φ(k)如式(5,6)所示。

(5)

(6)

式中：N1(k)和N2(k)分别表示环境噪声n1(t)和n2(t)的傅里叶变换。

在实际环境中，环境噪声和混响噪声并存且较严重时，采用单一的ML或PATH加权函数，时延估计的准确性会大大降低，在此基础上进行曲线拟合和Sinc插值等分数时延估计时，算法性能会严重下降。因此，为加强算法性能对于噪声的鲁棒性，提高时延估计精度，提出了广义互相关-最大似然相位补偿(GCC-Maximum likelihood phase compensation,GCC-MLP)相位补偿分数时延估计算法。

2.2 GCC-MLP相位补偿分数时延估计算法

对式(1,2)两边进行傅里叶变换,可得

(7)

由式(7)可得到信号频域能量等式

(8)

(9)

式中p表示混响能量比例系数。由式(8，9)化简可得，总的噪声能量

(10)

令q=p/(1+p)，则

(11)

将式(10)代入式(5)中，可得改进的频域加权函数

(12)

事实上，φMLP(k)可以简单地写成ML加权函数和PATH加权函数的线性表达，即

(13)

GCC-MLP算法中，φMLP(k)加权函数兼具了GCC-PATH和GCC-ML算法的优点，将φMLP(k)加权函数代入式(4)，可以估计得到整数采样时延单元值N1。根据实际环境中混响能量，合理地确定q值，能够有效地抑制混响噪声和环境噪声，大大提高整数采样时延单元估计准确率。进一步地，在整数采样时延单元估计的基础上，可以进行分数采样时延单元估计。传统的分数时延算法，如曲线拟合、sinc插值等，这些方法往往是在时域对广义互相关函数R12(n)进行曲线拟合，这类方法同样对环境噪声和混响噪声比较敏感，限制了分数延时估计精度的进一步提高。

由傅里叶变换性质可知，信号在时域的时延，在频域表现为相位变化，并且这一相位变化随频率呈线性关系。因此，通过在互相关频域补偿的线性相位可以估计信号时延，由于相位变化的连续性，估计得到的时延单元精度可以小于一个时间采样单元。GCC-MLP相位补偿算法利用经过φMLP(k)加权的互相关谱估计时延，能有效抑制环境噪声和混响噪声。假设实际的时延值为Ns，在整数采样延时单元N1估计准确的情况下，Ns∈(N1-0.5,N1+0.5]。根据离散傅里叶变换公式，在(N1-0.5,N1+0.5]区间的互相关频谱R(m)为

(14)

式中：C表示插值率(大于1的正整数)。假设此时互相关频谱R12(m)的绝对值峰值位于N2处，那么在R(N2)附近采用抛物线近似，根据式(15)可求得精确时延单元估计值

(15)

3 仿真数据结果

3.1 仿真参数

为验证算法的有效性，模拟声学环境，平面示意图如图3所示，假设声源和麦克风阵列都在同一水平高度。

(1) 房间模型几何参数房间大小为6 m×4 m×3 m；声源S坐标(XS,YS)为(3.6,3.8)；麦克风阵列中心坐标为O(3,1)；麦克风间距为d=5 cm。

(2) 噪声模型参数：环境噪声为高斯白噪声(信噪比SNR=0～20 dB)；混响噪声为IMAGE模型[9](混响时间T60=100～400 ms)。

(3) 语音信号参数：采样频率为Fs=32 kHz；每帧采样点数为N=4 096；语音信号长度为L=4 096×100帧。根据仿真参数计算可得，声源S信号分别到达Mic1和Mic2的时延τ12所对应的理论时延单元N1=1.487，声源偏向角θ=71.56°。

图3 模拟声学环境平面示意图Fig．3 Schematic plan of simulated acoustic environment

3.2 整数时延单元估计正确率分析

图4 整数时延估计准确率曲线1(T60=100 ms) 图5 整数时延估计准确率曲线2(T60=400 ms) Fig．4 The first accuracy rate curve of integer delay estimation(T60=100 ms) Fig.5 The second accuracy rate curve of integer delay estimation(T60=400 ms)

利用GGC-MLP算法进行整数部分时延估计，考察整数时延估计的准确率，并与GCC-ML算法和GCC-PATH算法进行性能比较。假设估计得到整数时延值为N1，若满足Ns∈(N1-0.5,N1+0.5]，则表示整数部分时延估计准确。图4,5分别为3种算法在混响时间T60= 100 ms(q=0.1)和T60=400 ms(q=0.3)条件下，整数时延估计准确率随信噪比SNR变化曲线图。对比分析图4,5，可以发现：

(1)GCC-ML算法对于环境噪声的鲁棒性较强，在低信噪比(SNR=0～5 dB)条件下，整数时延估计准确率远高于GCC-PATH；但是GCC-ML算法对于房间混响比较敏感，当房间混响较大时，算法性能会大大降低。

(2)GCC-PATH算法能有效抑制混响噪声，在高混响(T60=400 ms)、高信噪比(SNR=10～20 dB)情况下，算法性能优于GCC-ML，但是GCC-PATH对于环境噪声鲁棒性较差，当信噪比较低时，算法性能会严重下降。

(3)GCC-MLP算法结合了GCC-PATH算法和CGG-ML算法的优点，对混响噪声和环境噪声都有较强的抑制作用。在高混响、低信噪比条件下，整数时延估计准确率仍能达到95%以上。

3.3 分数时延单元估计误差分析

图6 分数时延均方根误差曲线(T60=100 ms) Fig．6 RMSE curve of subsample delay estimation (T60=100 ms)

在利用GCC-MLP算法整数时延单元估计的基础上，分别采用MLP-相位补偿、MLP-曲线拟合和MLP-Sinc[10]插值3种算法进行分数采样时延单元估计，其中插值率C=32。在不同混响条件下，时延估计均方根误差随信噪比变化曲线如图6,7所示。图6中，混响时间T60=100 ms，相同信噪比条件下，MLP-相位补偿算法估计所得时延均方根误差远远小于其他两种算法，尤其在低信噪比(SNR=0～5 dB)情况下，算法优越性充分得以体现。图7对比图6，混响时间T60由100 ms(q=0.1)变为400 ms(q=0.3)，相同信噪比条件下，相同算法的时延估计均方根误差均有所增加，但是比较误差增加量可以发现，MLP-相位补偿算法受混响噪声影响较小。由分析可知，MLP-相位补偿分数时延估计算法对于环境噪声和混响噪声都有较强抑制，算法鲁棒性优于MLP-曲线拟合和MLP-Sinc插值算法。

3.4 声源偏向角角度估计误差分析

根据估计得到的时延值，由式(3)可以求得声源偏向角。图8所示为同一混响条件下声源偏向角度均方根误差随信噪比变化曲线。由图可知，即使在高混响条件(T60=400 ms)下，GCC-MLP相位补偿算法估计声源偏向角的角度误差Δθ<2°，角度估计误差小于其他两种算法。

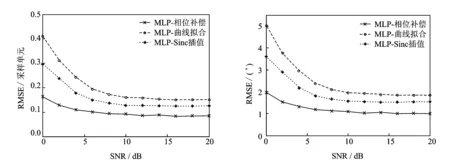
图7 分数时延均方根误差曲线(T60=400 ms) 图8 声源偏向角度均方根误差曲线(T60=400 ms)Fig. 7 RMSE curve of subsample delay estimation (T60=400 ms) Fig．8 RMSE curve of deflection angle of sound source (T60=400 ms)

4 结束语

在实际环境中，采用传统的分数时延估计算法，时延估计值受到环境噪声和混响噪声影响，声源角度估计误差较大。本文提出了一种GCC-MLP相位补偿分数时延估计算法，该算法改进了GCC频域加权函数，综合了GCC-ML和GCC-PATH加权函数的优点；与此同时，利用线性相位补偿和抛物线拟合，实现了连续的分数时延估计。GCC-MLP相位补偿分数时延估计算法相比于曲线拟合sinc插值算法，增强了算法对于噪声和声源位置的鲁棒性，进一步提高了时延估计精度。通过两阶段的时延估计，GCC-MLP算法能够实现精确的声源角度估计，角度估计误差小于2°。GCC-MLP相位补偿分数时延估计算法可以广泛用于声源角度估计和声源定位。

[1] 王瑞, 陈砚圃, 张恒. 声源定位中波达角一致性检测方法[J]. 数据采集与处理, 2010, 25(6): 756-760.

Wang Rui, Chen Yanpu, Zhang Heng. Method for detecting DOA homogeneity in sound source localization[J].Journal of Data Acquisition and Processing, 2010, 25 (6): 756-760.

[2] 周康辉, 董万胜, 刘恒毅, 等. 利用二次相关改进的广义互相关时延估计算法[J]. 数据采集与处理, 2013, 28(6): 801-806.

Zhou Kanghui, Dong Wansheng, Liu Hengyi, et al. Improved generalized cross correlation method for time delay estimation by using second correlation[J]. Journal of Data Acquisition and Processing, 2013, 28(6): 801-806.

[3] Wu W C, Chen O T C. Multiple-sound-source localization scheme based on feedback-architecture source separation[C]// 52nd IEEE International Midwest Symposium on Circuits and Systems. [S.l.]:IEEE, 2009: 669-672.

[4] Bai Y C, Zhang X G, Tang L. Subsample time delay estimation based on phase spectrum of band limited stochastic signals[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2010, 27(2): 170-175.

[5] Chen J C, Hudson R E, Yao K. Maximum-likelihood source localization and unknown sensor location estimation for wideband signals in the near-field[J]. Signal Processing, IEEE Transactions on, 2002, 50(8): 1843-1854.

[6] Perez-Lorenzo J M, Viciana-Abad R, Reche-Lopez P, et al. Evaluation of generalized cross-correlation methods for direction of arrival estimation using two microphones in real environments[J]. Applied Acoustics, 2012, 73(8): 698-712.

[7] Mosorov V. Phase spectrum method for time delay estimation using twin-plane electrical capacitance tomography[J]. Electronics Letters, 2006, 42(11): 630-632.

[8] Qin B, Zhang H, Fu Q, et al. Subsample time delay estimation via improved GCC PHAT algorithm[C]//2008 9th International Conference on Signal Processing. [S.l.]:IEEE,2008: 2579-2582.

[9] Allen J B, Berkley D A. Image method for efficiently simulating small-room acoustics[J]. The Journal of the Acoustical Society of America, 1979, 65(4): 943-950.

[10]Nakamura K, Nakadai K, Okuno H G. A real-time super-resolution robot audition system that improves the robustness of simultaneous speech recognition[J]. Advanced Robotics, 2013, 27(12): 933-945.

Improved Fractional Time Delay Estimation Method and Its Application

Liu Chao1,2, Bai Yechao1,2, Zhang Xinggan1,2

(1.School of Electronic Science and Engineering, Nanjing University, Nanjing, 210023, China；2.State Key Laboratory of Millimeter Waves, Southeast University， Nanjing, 210096, China)

Traditional fractional time delay estimation (TDE) algorithm is sensitive to ambient noise and reverberation noise, and the algorithm performance is severely degraded in the complex environment. To improve the accuracy of time delay estimation, a GCC-maximum likelihood phase compensation (GCC-MLP) phase compensation fractional time delay estimation approach is proposed based on generalized cross correlation(GCC). The frequency domain weighting function is also improved for GCC algorithm. At the same time, linear phase compensation is applied to the cross correlation spectrum in frequency domain and a continuous time delay estimator is obtained. Simulation comparition between the proposed algorithm and the other fractional TDE algorithms demonstrates that the proposed algorithm outperforms the curve fitting algorithm and the sinc interpolation algorithm. Meanwhile the robustness to the noisy and the reverberant conditions is reinforced, the time delay estimation error also decreases. Therefore, GCC-MLP phase compensation fractional time delay estimation algorithm can be widely used in sound source direction of arrival estimation and sound source localization.

generalized cross-correlation(GCC)； fractional time delay estimation； microphone array； sound source direction of arrival estimation； phase compensation

江苏省产学研前瞻性联合研究(BY2012187)资助项目；毫米波国家重点实验室开放课题(K201514)资助项目。

2014-05-12；

2014-10-06

TN911.72