一种新的社区/动态社区优化方法*

2015-12-26李亚芳贾彩燕刘光明

数据采集与处理 2015年6期

关键词：指派动态节点

李亚芳贾彩燕于剑刘光明

(1.北京交通大学计算机与信息技术学院，北京，100044； 2.交通数据分析与挖掘北京市重点实验室，北京，100044)

一种新的社区/动态社区优化方法*

李亚芳1,2贾彩燕1,2于剑1,2刘光明1,2

(1.北京交通大学计算机与信息技术学院，北京，100044； 2.交通数据分析与挖掘北京市重点实验室，北京，100044)

社区结构作为复杂网络的重要拓扑特性之一，成为当前的研究热点。本文提出了一种基于边排序和模块度优化的社区发现方法。该方法首先对初始的静态网络进行稀疏化，然后在稀疏化后的网络上依据边的重要程度对边进行排序，给出了一种模块度最大化、快速边合并的社区发现方法(Fast rank-based community detection, FRCD)。在初始网络社区划分结果的基础上，将该方法推广到动态、实时社区划分上，给出了一种快速、鲁棒的动态社区划分方法(Incremental dynamic community detection, IDCD)。理论分析表明FRCD相对于边具有线性时间复杂度。在实际和人工网络上的实验结果均表明，本文提出的方法无论在静态网络社区划分还是在动态网络社区追踪上都优于已有方法。

社区发现；模块度；边排序；动态性

引言

现实世界中，很多系统都以网络形式存在，如社会系统中的人际关系网、科学家合作网和流行病传播网，生态系统中的神经元网、基因调控网和蛋白质相互作用网，科技系统中的电话网、因特网和万维网等。近年来，复杂网络研究已成为最重要的多学科交叉研究领域，吸引了越来越多研究者的目光。研究者发现很多实际的网络具有“模块性”[1]，即网络组织结构表现出明显的社区结构，表现为社区内部连接稠密，社区间连接稀疏的中观尺度结构。找到网络中连接紧密的簇结构有助于更深入地了解网络的本质，认识网络结构与其功能之间的关系，发现复杂网络中的规则并对其行为进行预测。社区结构可以揭示出社会系统的组织结构及随时间演化的关系，蛋白质功能和蛋白质物理相互作用间的内在联系以及网页主题和超连接间的内在关系等。

随着对复杂网络中社区结构分析的需求不断增强，目前关于社区发现研究的方法和成果很多。如经典的基于节点分裂的GN算法[1]、基于模块度优化的BGLL[2]和CNM算法[3]、基于标签传播 (Label propagation algorithm, LPA)算法[4]以及基于随机游走和压缩编码的Infomap算法[5]等。目前，网络类型多样化，针对网络的不同类型提出的针对多模式和多内容网络的社区检测方法[6-7]。在以上社区发现算法中，由于模块度能够作为一种衡量网络中社区结构的内部指标，最大化模块度以探测网络社区结构的算法(如BGLL和CNM)在很多领域得到了较成功的应用[2-3]。然而，BGLL和CNM等方法只能对一段时间累积下的静态网络进行划分，无法实时追踪网络社区结构的变化，需要对相邻时间快照得到的网络重新进行社区划分，并保存每一时间快照下的社区结构。由于实际的动态社会网络具有时间局部性，相邻时间间隔的网络结构变化相对缓慢[8-9]。因此，对于非常相似的网络反复进行社区划分，会产生了很多重复的操作，从而降低算法的效率。

Shang等[10]对BGLL算法进行了扩展，该方法首先利用BGLL算法在初始子网络上得到一个初始的社区划分结果，然后通过随机加边的方式模拟网络的增长，将新增节点不断实时分配到已有社区之中。但是该方法存在以下两个问题：(1)该方法属于两阶段方法，依赖于BGLL算法得到的初始社区划分，当初始子网络过小或选择时机不当而不能保证较好的初始划分时，难以得到理想的动态社区划分结果。对不断增长的动态网络，如何选择一个合适的初始子网络是该方法存在的一个问题；(2)由于Shang等的算法对下一个时刻增加的边采用随机处理的方法，导致不同的边处理顺序会得到不同的社区划分结果。因此，算法的性能不够稳定。针对以上问题，本文提出一种基于边排序的、模块度优化社区划分算法(Fast rank-based community detection, FRCD)。该算法是一种从头算法方法，对于静态网络能够得到较准确的社区划分结果。并且，其动态网络上的扩展算法(Incremental dynamic community detection, IDCD)对初始子网络依赖性小，在FRCD算法在初始子网络已有社区划分的基础上，能实时地处理以不同时间粒度为间隔的动态增加的网络结构，并且具有性能稳定的优点。

1 研究基础

模块度Q函数用网络中连接社区内部顶点的边所占的比例与随机网络中连接社区结构内部顶点的边所占比例的期望的差值来衡量网络中社区划分的质量[1,11]，其定义如下

(1)

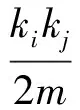
显然，模块度越大、网络的社区结构越明显。因此，对于一个给定的网络，可以通过最大化Q函数得到了一个较好的社区划分结果(如BGLL算法[2]，CNM算法[3])。

通过对模块度Q函数进行变形，可将其转换为以下形式[10]

(2)

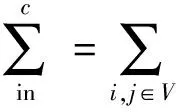
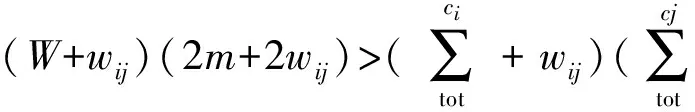
2 FRCD算法

基于网络局部稀疏和排序的静态社区模块度优化算法FRCD可分为3个步骤：计算边的相似度、对网络进行局部稀疏化及边排序、节点社区指派及社区合并。本算法假设相似度越高的节点对，其关系越容易建立，在社区中所处的位置越靠近中心。

2.1 边相似度计算

计算边的强度的方法有很多，如边介数[1]、桥系数[12]以及边的聚集系数[12]等，这些方法都可以用于衡量两节点关系的紧密程度。但是这些方法有的基于网络全局结构，有的计算复杂度较高，对于大规模网络的处理代价较大。因此，本文采用一种基于局部的、计算简单的Jaccard相似度方法来计算网络中边(i,j)的强度。其中，i和j为与边(i,j)关联的两个节点。具体定义如下

(3)

式中：N(i)表示节点i的邻居节点的集合，N(i)∩N(j)为节点i和节点j共有邻居个数，N(i)∪N(j)为节点i和节点j总的邻居个数。

通过Jaccard相似度的定义可知：如果两个节点的共有的邻居越多，节点间的相似程度越高，边上的强度越大。根据本文的假设，如果两个节点的相似性越高，这两个节点间的关系更容易建立而且更加稳固，并且这两个节点在社区中所处的位置越靠近社区的中心。因此，首先按照边的排序对最容易建立关系的节点进行社区指派。然后，通过最大化模块度Q依次对其他节点进行社区指派。

2.2 网络局部稀疏化

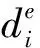
由于不同的网络稀疏指数，得到的结果不同。如果稀疏值设的太小，会造成网络过于稀疏，难以找到原始网络中蕴含的社区结构；设得太大，不能有效加快算法运行速度。因此，通过实验选择e=0.5来对网络进行稀疏化，此时在各种网络规模中均能得到较稳定的社区划分结果。显然，通过网络局部稀疏化，能够有效减小运算复杂度，从而提高算法的运行效率。

2.3 社区指派和合并

依据假设，对稀疏化的网络按照边的相似度进行降序排序后，首先将排序在第一位的边上两个节点指派到同一个社区内，作为初始的社区。然后，按照排序顺序依次对后续的边中的节点进行社区指派，即把相对位于社区边缘的节点进行社区指派。其指派策略采用Shang等[10]动态社区指派策略。即根据边的4种类型，依次对节点进行社区指派。通过排序，能够保证得到比较稳定的社区结构。社区指派后，需要通过社区的合并对指派的结果进行进一步优化，从而得到更符合实际的划分结果。需要进行社区合并的小社区需要满足以下两个条件。

(1)不满足弱社区的定义[14]。

如果社区A不满足

(4)

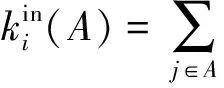
(2)社区合并需要保证网络的模块度Q值不会减少。

本文提出了一种基于边排序的模块化最大化社区发现算法FRCD，其整体流程如下。

输入：网络G=(V，E)，稀疏化指数e。

输出：社区结构，节点列表。

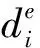
2.4 算法的时间复杂度分析

3 IDCD算法

任给一个网络，应用FRCD算法可以对该网络进行社区划分。相应于Shang等的方法，FRCD算法可以自然地扩展到对动态网络社区划分上，以实时的追踪网络结构的变化。由于现实中的社会网络结构变化都是很缓慢的，合适的相邻采样时刻之间网络变化很小。因此，通过调整时间间隔，能够对不同时间粒度内增加的节点进行社区指派。

如果选取的时间粒度以一条边的增加为粒度，称其为基本元粒度。此时，只需要判断该边所属的类型，根据边的类型采取相应的操作，实现边关联的节点的社区指派。在一定的时间间隔内，当增加的边由多个基本元粒度边构成时，称之为一定时间粒度。此时IDCD算法对新增的边根据关联节点是否出现在节点社区指派列表中分为3类：全新列表(都没有进行社区指派)，半新列表(至少一个节点已经进行了社区指派)，已有列表(都进行社区指派)。类似地，根据Jaccard相似度和节点的度可以对已有列表和半新的列表中的边进行降序排列，进而由边的重要程度逐个对边关联的节点进行社区指派，并更新节点社区归属列表，算法流程如下。

输入：t-1时刻网络的社区结构，原网络以及新增的网络，节点列表。

输出：t时刻的社区结构，更新的节点列表。

(1)对新增的节点和边，根据节点列表分成3类；(2)根据原网络对新增边计算相似度，按照相似度和度进行降序排序；(3)在t-1时刻得到的社区结构基础上，对新组合的新增列表中的节点依次进行社区指派；(4)更新节点社区归属列表。

4 实验结果与分析

为了定量地测试本文提出算法的有效性，分别在真实网络数据和人工生成数据上测试了新给出的FRCD算法与基于模块度优化的BGLL算法以及CNM算法的社区划分效率。同时，给出了FRCD算法在不进行网络稀疏化时的划分结果(记为FRCD*)。在人工网络上模拟了当网络动态变化时，新给出的动态社区划分方法IDCD和Shang等给出方法的社区划分的差异。

由于这两类数据集都已知社区结构，因此选取了标准化互信息(Normalized mutual information, NMI)[14]以及准确率[15]作为社区划分结果优劣的评价指标。其中，NMI的定义为

(5)

4.1 静态社区结构的实验比较

4.1.1 真实实验数据

在本节实验中用到的真实数据包括经典的美国大学足球赛网络Football[16]，Zachary空手道俱乐部网络Karate[17]]以及海豚关系网络Dolphins[18]。除了这3个经典实际网络，为了测试该算法在不同规模真实网络中的社区划分效果，本文还选取其他3个实际网络，包括美国政治书籍网络Political Books[19]，博客网络Blogs[20]以及蛋白质交互网络PPI[21]，各网络相关属性如表1所示。

表1 真实网络数据集

由于本文提出算法是基于模块度优化的社区发现方法，首先将FRCD与BGLL和CNM算法进行实验比较。Shang等人提出的方法缺乏稳定性，导致程序每次运行的结果不同，因此选择10次运行结果中得到Q值最大的结果进行对比，得到表2～4所示的实验结果。

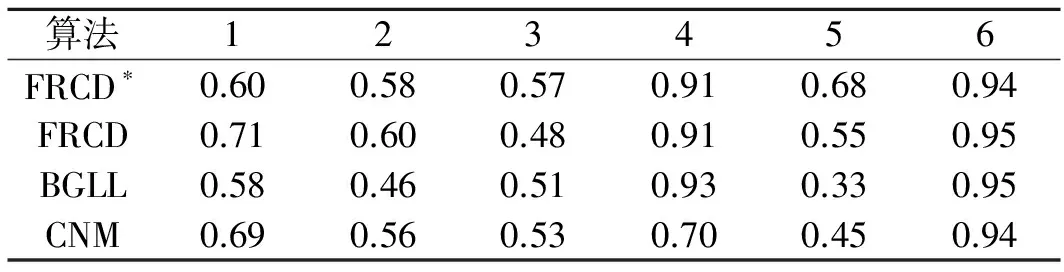
表2 真实网络中的NMI对比结果

表3 真实网络中的Accuracy对比结果

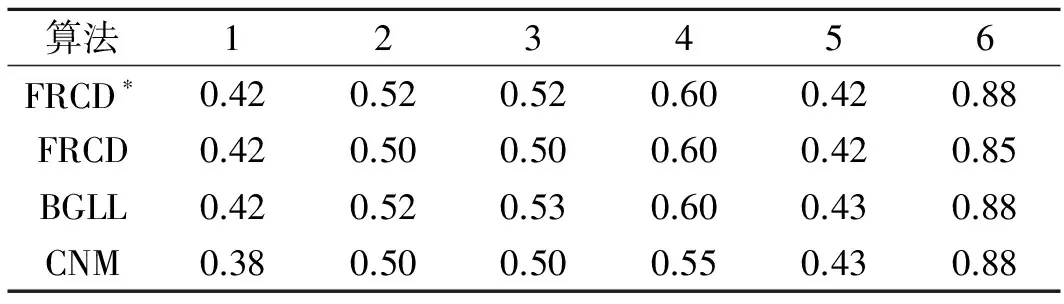
表4 真实网络中的Q对比结果

通过实验结果比较可以发现：(1)FRCD算法在各网络中得到的最优模块度值与BGLL大致相同，都具有较高的模块度；(2)在Karate，Dolphins，Political Books以及blogs网络上得到的NMI以及准确率要优于BGLL；(3)网络的稀疏化能够减少社团间的部分连边，同时会对社团内部节点间的连边进行稀疏，此时得到的结果与未稀疏化网络相比，会优于或者略差于未稀疏化的网络。在Karate和Dolphins网络上得到的NMI以及在Football网络上得到的准确率明显优于未稀疏化后的网络，但是在Political Books网络上效果略差，因此稀疏化的程度会对算法的准确性产生一定的影响。FRCD算法能够较准确地发现网络中蕴含的社区结构。

4.1.2 人工网络数据

为进一步实验验证本文算法的效果，本文选用Lancichinetti等提出的LFR人工网络[22]进行比对，表5给出了生成的4个LFR人工网络的参数设置。

表5中，N表示生成的网络中节点的个数；MU是网络的混合参数，表示与社区内节点关联的边中处于社区之间边的比例，该值越小表明生成的网络的社区结构越清晰，取值为0.1到0.9；k表示网络的平均度；kmax表示网络中节点的最大度；minc表示网络中最小社区中节点个数；maxc表示网络中最大社区中节点的个数；t1为度分布的负指数值；t2为网络中社区规模分布的负指数值。通过与BGLL和CNM进行比较，得到图1～4的实验结果。

表5 LFR人工网络中的参数

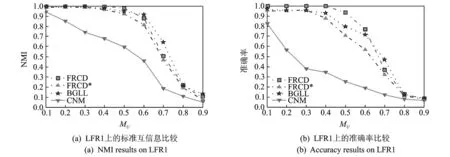
图1 LFR1上的实验比较Fig.1 Experimental results on LFR1

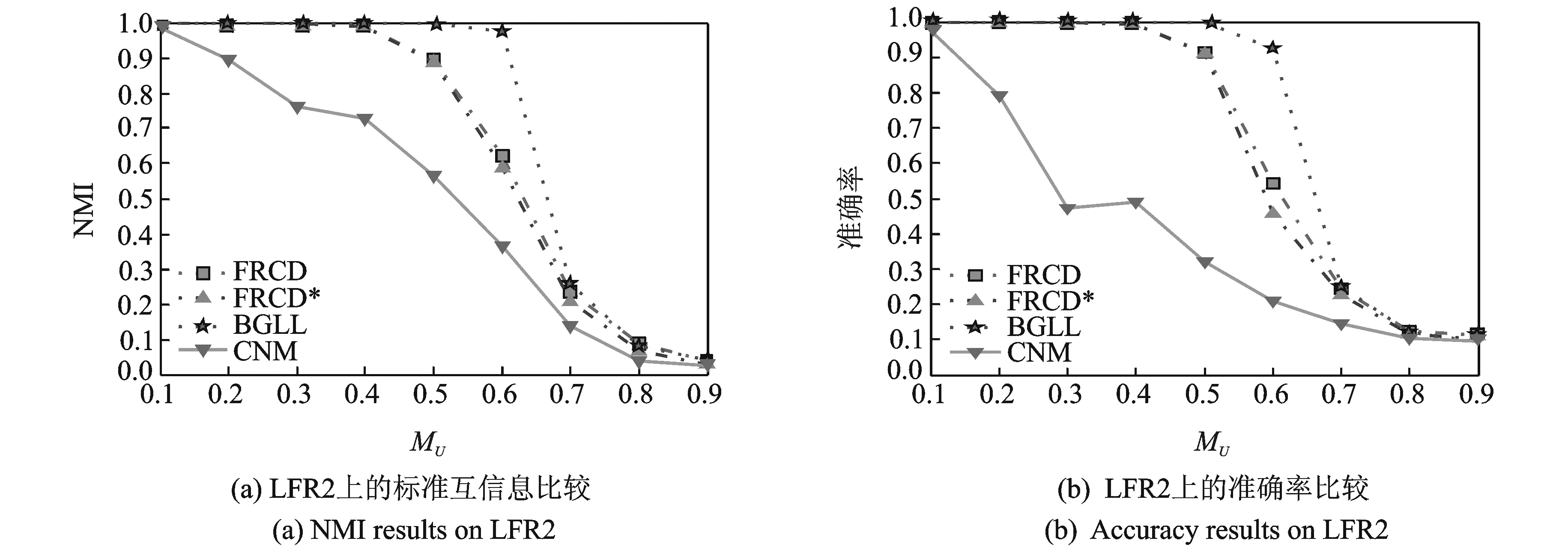
图2 LFR2上的实验比较Fig.2 Experimental results on LFR2

图3 LFR3上的实验比较Fig.3 Experimental results on LFR3

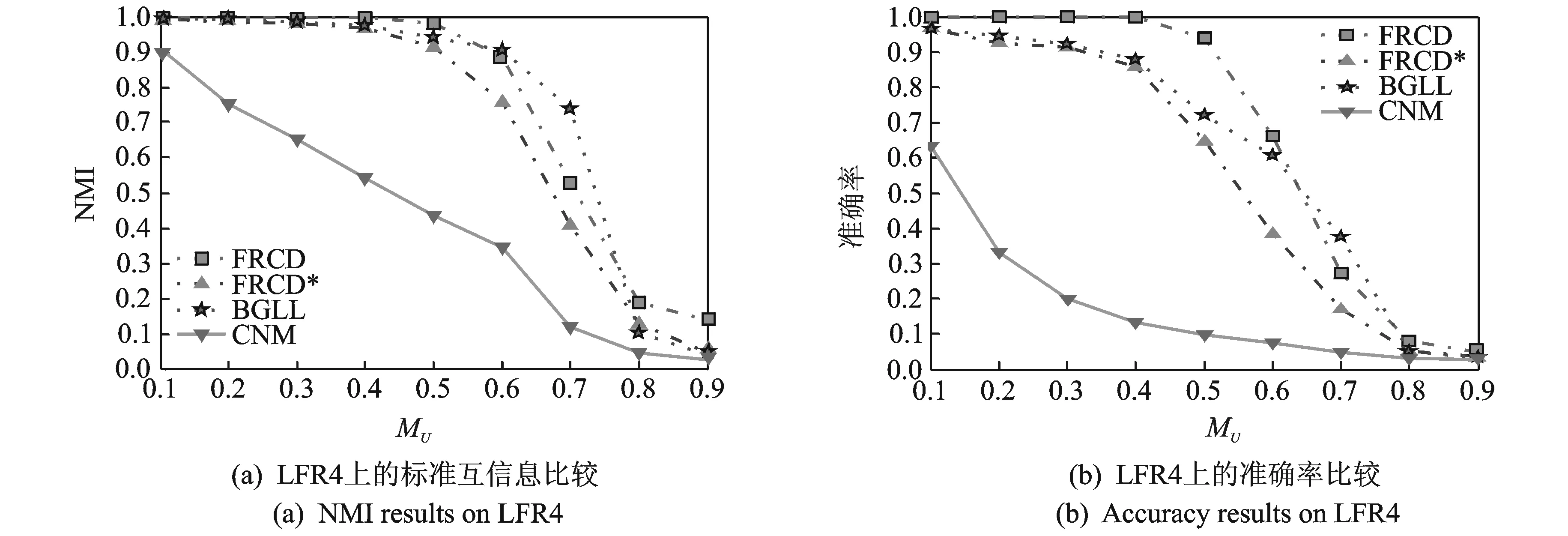
图4 LFR4上的实验比较Fig.4 Experimental results on LFR4

通过在人工生成网络上的实验比较可知，当网络混合参数取不同值时，FRCD算法大部分情况优于BGLL和CNM，尤其是MU=0.1～0.4时能得到完全准确划分。但是当MU=0.7时，此时网络社区结构不够清晰，效果不如BGLL。整体的实验结果可知FRCD在静态社区结构发现中，能得到较准确的社区结构。

4.2 动态网络的实验比较

由于现实中的社会网络结构变化都很缓慢，相邻采样时刻之间网络变化很小，因此通过对人工网络随机抽取的方法，模拟增加的网络。具体生成方法如下。

输入：含有n个节点的网络G0，增量网络个数N。

输出：初始静态网络，以及后续的增量网络G1,…,GN，其中Gr为第r个增量网络，初始r=1。

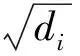
在实验中，设β1=0.01，β2=0.005，N=10。分别在LFR1和LFR3中，当mu=0.3时，和Shang等人提出的方法进行实验比较，由于Shang方法具有随机性，因此采用10次实验结果的平均值和提出的IDCD算法进行比较，横坐标为增加各子集个数，实验结果如图5，6所示。

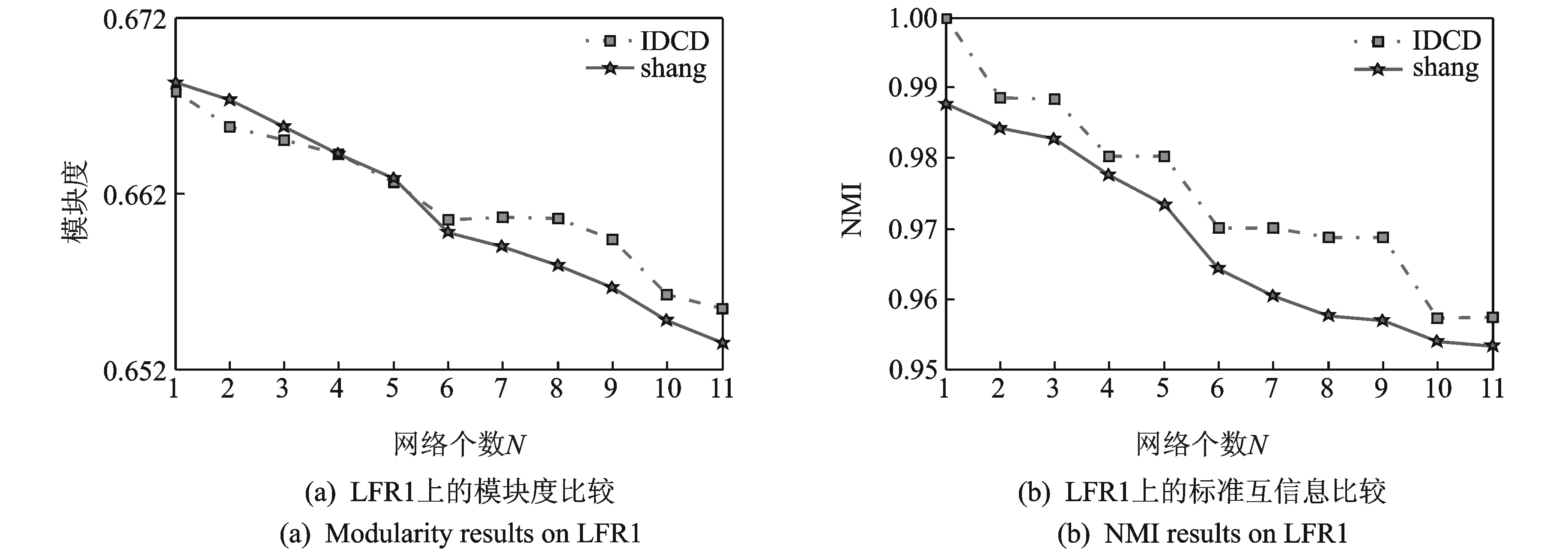
图5 LFR1上动态社区结果Fig.5 Dynamic community detection results on LFR1

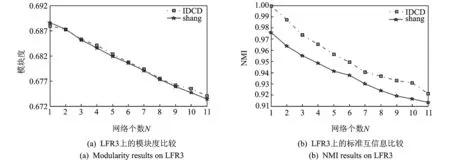
图6 LFR3上动态社区结果Fig.6 Dynamic community detection results on LFR3

通过与Shang等提出的方法进行比较，可以看到：随着时间的推移，增量式的动态社区发现方法由于存在错误率累积的问题，得到的结果整体呈现变差趋势；本文提出的IDCD方法在起初阶段效果略差于BGLL，但是随着网络规模的增大，得到的效果逐渐优于Shang等人的方法，从而说明本文算法在处理动态网络时的有效性。

5 结束语

本文提出了一种新的基于模块度优化的社区发现方法，该方法不仅能够发现静态网络中的社区结构，而且可以对动态增加的网络进行实时的社区结构追踪。通过在实际网络和人工生成网络中与基于模块度最大化的BGLL和CNM算法进行比较，表明本文提出的静态社区发现方法FRCD具有较高的划分准确率。进一步通过在动态网络中与Shang等人的方法进行实验对比，说明IDCD算法能够有效追踪网络社区结构的变化，对Shang方法存在的问题进行了有效改进。另外，本文所给出的算法是一种基于模块度优化的社区发现方法，可以用于优化其他的目标函数，如模块度密度[23]、Surprise[24]等。但本文中的算法在进行动态网络追踪时，只考虑了网络规模不断增大的情形。虽然，这在一定程度上符合实际网络规模的变化，但是在现实世界中也存在部分节点和边在下一个时刻消失的情况。目前，这在动态网络研究中仍是一个研究难点，也是未来要探索解决的问题之一。

[1] Girvan M, Newman M E J. Community structure in social and biological networks[J]. PNAS, 2002,9(12):7821-7826.

[2] Blondel V D, Guillaume J L, Lambiotte R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008(10):P10008.

[3] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004,69(2):026113.

[4] Raghavan U N, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks[J]. Physical Review E, 2007,76(3):036106.

[5] Rosvall M, Bergstrom C T. Maps of random walks on complex networks reveal community structure[J]. Proceedings of the National Academy of Sciences, 2008,105(4):1118-1123.

[6] Tang L, Liu H, Zhang J, et al. Community evolution in dynamic multi-mode networks[C]∥Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2008:677-685.

[7] Tang L, Liu H, Zhang J. Identifying evolving groups in dynamic multimode networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2012,24(1):72-85.

[8] 单波,姜守旭,张硕,等.IC:动态社会关系网络社区结构的增量识别算法[J].软件学报,2009,20:184-192.

Shan Bo, Jiang Shouxu, Zhang Shuo, et al. IC: Incremental algorithm for community identification in dynamic social networks[J]. Journal of Software, 2009,20:184-192.

[9] 周耀明,李弼程.一种自适应网络舆情演化建模方法[J].数据采集与处理,2013，28(1):69-76.

Zhou Yaoming, Li Bicheng. Adaptive evolution modeling method of internet public opinions[J]. Journal of Data Acquisition and Processing, 2013，28(1):69-76.

[10]Shang J, Liu L, Xie F, et al. A real-time detecting algorithm for tracking community structure of dynamic networks[C]∥The 6th SNA-KDD Workshop. New York, USA: ACM, 2012.

[11]Park J, Newman M E J. The origin of degree correlations in the Internet and other network[J]. Phys Rev E, 2003,68(2):026112.

[12]Cheng X Q, Ren F X, Shen H W, et al. Bridgeness: A local index on edge significance in maintaining global connectivity[J]. Journal of Statistical Mechanics: Theory and Experiment,2010(10):P10011.

[13]Satuluri V, Parthasarathy S, Ruan Y. Local graph sparsification for scalable clustering[C]∥Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data. NewYork, NY, USA: ACM, 2011:721-732.

[14]Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004,101(9):2658-2663.

[15]Danon L, Diaz-Guilera A, Duch J, et al. Comparing community structure identification[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005(9):P09008.

[16]Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002,99(12):7821-7826.

[17]Zachary W. An information flow model for conflict and fission in small groups1[J]. Journal of Anthropological Research, 1977,33(4):452-473.

[18]Lusseau D, Schneider K, Boisseau O J, et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology, 2003,54(4):396-405.

[19]Newman M E J. Modularity and community structure in networks[J]. Proceedings of the National Academy of Sciences, 2006,103(23):8577-8582.

[20]Adamic L A, Glance N. The political blogosphere and the 2004 US election: Divided they blog[C]∥Proceedings of the 3rd International Workshop on Link Discovery. NewYork, NY, USA: ACM, 2005:36-43.

[21]Vlasblom J, Wodak S J. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs[J]. BMC Bioinformatics, 2009,10(1):99.

[22]Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms[J]. Physical Review E, 2008,78(4):046110.

[23]Li Z, Zhang S, Wang R S, et al. Quantitative function for community detection[J]. Physical Review E, 2008,77(3):036109.

[24]Aldecoa R, Marín I. Deciphering network community structure by surprise[J]. PLoS One, 2011,6(9):e24195.

Novel Community/Dynamic Community Optimization Algorithm

Li Yafang1,2， Jia Caiyan1,2， Yu Jian1,2, Liu Guangming1,2

(1.School of Computer and Information Technology, Beijing Jiaotong University, Beijing, 100044, China; 2.Beijing Key Lab of Traffic Data Analysis and Mining, Beijing, 100044, China)

Community structure is one of the most important topological characteristics in the complex network, being a hot research area in different fields. A novel community detection algorithm is proposed based on edges rank and modularity optimization. Local graph is sparsificated and edges are ranked according to the similarity. Therefore, a method called the fast rank-based community detection (FRCD) by maximizing modularity and fast mergement of edges is achieved. Meanwhile the method is also extended to dynamic and real-time community detection on the basis of initial community structure, and a fast and robust dynamic community detection algorithm called the incremental dynamic community detection (IDCD) is presented. Theoretical analysis exhibit that FRCD has linear complexity for network edges. Experimental results in real-world and artificial networks demonstrate the high accuracy and good performance of the algorithm on static community detection and tracking dynamic structure of networks.

community detection; modularity; rank; dynamic characteristic

国家自然科学基金(61473030,61370129)资助项目;北京市自然科学基金(4112046)资助项目;北京市科委(Z131110002813118)资助项目;中央高校基本科研业务费专项基金(K15JB00070,2014JBM031)资助项目;北大方正集团有限公司数字出版技术国家重点实验室开放课题资助项目。

2014-03-25；

2014-10-23

TP181