本质有穷的亚纯函数的Borel例外值

蔡惠京

(中山市广播电视大学，广东中山，528402）

本质有穷的亚纯函数的Borel例外值

蔡惠京

(中山市广播电视大学，广东中山，528402）

对于复平面上的亚纯函数，推广通常的增长级为p阶增长级，引进本质有穷的概念，进而研究本质有穷的亚纯函数的Borel例外值的存在性。将通常意义下有限级全纯函数的Hadamard因子分解定理和关于整函数组的Borel定理推广到本质有穷的亚纯函数上来，在此基础上，将熟知的有限级亚纯函数的Borel例外值定理推广到本质有穷亚纯函数的情形。

亚纯函数；增长级；例外值

1 引言与主要结果

定理A 如果f(z)是超越的，则对于任意有限或无限的复数a，方程

f(z) = a

有无穷多个解，至多有两个a值例外。

人们称上述定理中的例外值为亚纯函数f(z)的Picard值。

为了推广Borel定理，Nevanlinna引进了亚纯函数f(z)的特征函数T(r,f)的定义，在此基础上给出了亚纯函数的增长级的概念，进而给出如下：

则对于任意有限复数a，都有

人们称定理B中的例外值为亚纯函数f(z)的Borel值。

为f(z)的p阶增长级，这里

相应地，我们还要推广定义1为如下的：

据此，本文将定理B推广为如下：

我们称上述定理中的例外值为亚纯函数f(z)的p阶Borel值。

Valiron曾经将Borel值进行了细分，并对于全纯函数将Borel定理推广为[7]：

(3) 如果a是f(z)的一个Borel值，则对于任意复数的单零点序列的收敛指数都等于f(z)的增长级。

Singh和Gopalakrishna将Valiron的结果推广到了有限级亚纯函数的情形[8,9]。本文我们可以进一步将他们的结果推广到本质有穷的亚纯函数的情形。我们将证明如下：

2 几个引理

为证明我们的结论，需要用到几个引理。

引理1 （Nevanlinna第一基本定理）设f(z)是亚纯函数，则对于任意有限复数a，皆有

由此可知，p阶有穷的亚纯函数全体关于加法和乘法运算形成一个域。

不难得到：

便得到(2.1)式。

便得到(2.2)式。

引理证毕。

引理证毕。

是全纯函数，且成立：

便易得证引理结论。

3 亚纯函数的Hadamard因子分解定理

本节，我们借助于引理4，将Hadamard关于整函数的因子分解定理推广为：

且成立下述结论：

证明：由引理3知，f(z)的零点序列和极点序列都是p阶有穷的。用表示f(z)的全部零点序列形成的典型乘积，表示f(z)的全部极点序列形成的典型乘积，再由引理3和引理4，就得到(4.2)式。

因而可得：

至此，定理4得证。

这是我们在文[6]中给出的本质有穷的全纯函数的Hadamard因子分解定理。

作为定理4的应用，我们可以给出下列：

这就得到

于是由

定理5得证。

上述定理表明：本质有穷的全纯函数关于复合运算是封闭的。

4 全纯函数组的Borel定理

Borel曾经对于全纯函数组证明了一个在整函数值分布研究中有着极其重要作用的结论[11]：

而由条件(2)，上式右端亚纯函数的p阶增长级小于左端函数的p阶增长级，矛盾！这一矛盾说明假设是不对的，因而定理结论成立。

对(4.4)式两端求导数，得到：

解微分方程，有：

故得证定理。

作为定理6的一个应用，我们可以将全纯函数的Borel例外值定理推广为关于Borel例外函数的定理。

至多有一个小函数例外。

5 定理1的证明

再结合(5.1)式，有：

以及

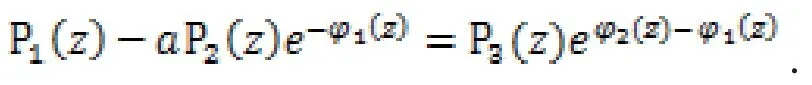
由上一段的讨论知，这也不可能。

于是定理1得证。

6 定理2的证明

本节，我们来证明定理2。为此，先借助定理4证明如下：

这就完成(1)的证明。

至多有两个值例外。

这就完成了定理2的证明。

7 定理3的证明

以及

由上式和(7.2)式，便得到：

此即：

这就完成了定理3的证明。

8 导函数的Borel值

Hayman曾经给出关于亚纯函数及其导数的Picard值的一个结果[13]：

这就完成了定理9的证明。

【参考文献】

[1]Nevanlinna R. Le théorème de Picard-Borel et la théorie des fonctions méromorphes[J]. Paris, 1929.

[2]Nevanlinna R. Analytic functions[M]. Berlin: Springer, 1970.

[3]仪洪勋，杨重骏. 亚纯函数的唯一性理论[M].北京：科学出版社，1995.

[4]Sato D. On the rate of growth of entire functions of fast growth[J]. Bull. Amer. Math. Soc., 1946, 52: 1046-1052.

[5]蔡惠京.关于高阶线性微分方程解的p阶增长性[J].广东广播电视大学学报，2014，6（23）：99—104.

[6]蔡惠京.本质有穷的全纯函数及其导数的Borel例外值[J]. 数学理论与应用,2015,2（35）:1-12.

[7]Valiron G. Lectures on the general theory of integral functions[M].New York: Chelsea Pub. Co., 1964.

[8]Singh S.K., Gopalakrishna H.S. Exceptional values of entire and meromorphic functions[J]. Math. Ann., 1971, 191: 121-142.

[9]Gopalakrishna H.S., Bhoosnuemath S.S. Borel exceptional values of differential polynomials[J]. Rev. Roum. Math. Fures et. Appl. 1978, 721-726.

[10]Pólya G. On integral function of an integral function[J]. J. London Math. Soc., 1926, 112: 12-15.

[11]Borel E. Sur les zéros des fonctions entières[J]. Acta Math.1897, 20: 357-396.

[12]杨乐. 值分布及其新研究[M].北京: 科学出版社, 1982.

[13]Hayman W. Picard values of meromorphic functions and their derivatives[J]. Ann. Of Math., 1959, 70: 9-42.

（责任编辑：楚和）

Borel Exceptional Values of Meromorphic Functions withEssentialFinite

CAI Hui-jing
(Zhongshan Radio & TV University, Zhongshan, Guangdong,China,528402)

In this paper, we fi rst introduce the concept of essential fi nite generalizing the common order of growth to the p-order of growth for meromorphic functions. Then the existence of Borel exceptional values of essential fi nite meromorphic functions and their derivatives are investigated. The Hadamard theorem has been proved for essential finite meromorphic functions. Therefore the famous Borel theorem has been generalized to essential fi nite meromorphic functions too. Finally, the existence theorem of Picard exceptional values of meromorphic functions and their derivatives are generalized to the existence theorem of Borel exceptional values of essential fi nite meromorphic functions and their derivatives.

meromorphic function; order of growth; Borel exceptional value

O174.52

A

2095－932x（2015）05－0100－09

2015－05－05

蔡惠京（1957－），男，湖南攸县人，中山市广播电视大学教授。