双曲正弦非线性跟踪微分器设计

卜祥伟,吴晓燕,张蕊,朱付景

(空军工程大学防空反导学院,710051,西安)



双曲正弦非线性跟踪微分器设计

卜祥伟,吴晓燕,张蕊,朱付景

(空军工程大学防空反导学院,710051,西安)

针对传统跟踪微分器算法复杂、参数整定困难和噪声抑制能力有限的不足,设计了一种新型双曲正弦非线性跟踪微分器(HNTD)。引入终端吸引子函数和双曲正弦函数构造了HNTD的跟踪函数,并证明了其全局一致渐近稳定性。通过仿真分析设计参数变化对HNTD频域特性的影响,为其设计参数的整定提供参考。双曲正弦函数既能保证HNTD状态收敛的快速性,又能有效避免平衡点附近的颤振现象;终端吸引子函数则保证了HNTD对噪声良好的抑制效果。仿真结果表明,HNTD的跟踪和滤波效果与传统跟踪微分器相比,不仅结构形式简单、设计参数相对较少、整定规则明确,而且在跟踪精度、响应速度和滤波能力等方面均具有一定的优势。

非线性跟踪微分器;终端吸引子函数;双曲正弦函数;抑制噪声

微分信号的精确提取对PID控制、反演控制和动态滑模控制等控制方法都有十分重要的意义,且在信号处理和参数估计中也有广泛应用。文献[1-3]提出的高阶滑模微分器的设计参数选取异常困难,且抖振问题无法解决,由于其在每一层滑模面上均含有输入信号,因此极易受到噪声污染。文献[4-5]虽然提出了一些改进措施,但并无突破性成果。我国韩京清研究员首次提出了跟踪微分器的概念,并给出了3种具体形式的跟踪微分器[6],但其跟踪和微分效果并不理想。文献[7]提出了一种新型跟踪微分器,但是跟踪精度不高,且微分输出存在抖振。文献[8]设计了一种高增益跟踪微分器,但是噪声抑制能力不强。为了改善微分器性能的不足,文献[9-12]提出了几种改进的跟踪微分器,它们基于一个共同的改进策略:在微分器设计中同时引入非线性环节和线性环节,在状态远离平衡点时,非线性环节可以保证微分器收敛的快速性;在状态接近平衡点时,线性环节可以保证微分器线性无颤振收敛。但是,这样设计的微分器结构形式过于复杂,待整定参数较多,微分器参数整定规则很难获取,工程实用性差。文献[13]设计了一种反正切形式的新型跟踪微分器,但是设计参数过多,且噪声抑制能力有限。

基于以上分析,本文设计了一种新型双曲正弦非线性跟踪微分器(HNTD)。双曲正弦函数可以保证HNTD收敛的快速性并能有效消除平衡点附近的输出颤振,终端吸引子函数使得HNTD对噪声不敏感。通过仿真分析了设计参数变化对微分器频域特性的影响,为其设计参数的整定提供了参考。最后进行了实例仿真,并与几种改进的微分器进行比较来验证HNTD在跟踪、微分和滤波性能上的优势。

1 HNTD设计

定理1 给定如下系统

(1)

如果满足a1>0,a2>0,b=q/p,q、p为终端吸引子设计参数[4-5],即p>q>0且q、p均为奇数,那么系统(1)在(0,0)全局一致渐近稳定。

双曲正弦函数sinh(·)变化过程和系统(1)的收敛过程如图1所示。

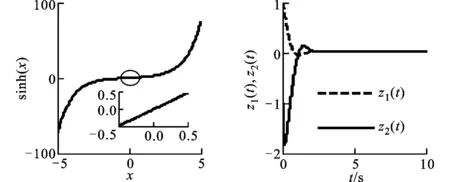
(a)变化过程 (b)收敛过程图1 sinh(·)变化过程和系统收敛过程

由图1可知:当系统状态离平衡点较远时,sinh(·)的非线性特性可以保证系统(1)以较快速度收敛;当系统状态离平衡点很近时,sinh(·)的线性特性可以保证系统(1)的平滑无抖收敛。因此,采用双曲正弦函数构造HNTD的跟踪函数,可以保证HNTD较好的跟踪、微分和滤波性能。

图1中的x、sinh(x)、z1(t)、z2(t)等状态都没有具体的物理意义,因此没有具体的物理单位。图3、图4中的输入信号、跟踪信号和微分信号也都没有具体的物理单位。

为了证明定理1,先给出如下引理。

引理1[14]考虑时不变系统

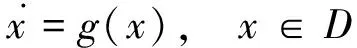
(2)

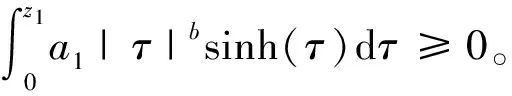
(3)

对W(z1,z2)求时间的全导数并结合式(1)得

(4)

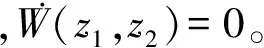
定理2 对于如下系统

(5)

如果满足R>0,a1>0,a2>0,b=q/p,p>q>0且q、p均为奇数,那么对任意常数T>0、可积函数υ(t),且υ(t)有界,则系统(5)的解x1(t)满足

(6)

即x1(t)平均收敛于υ(t),x2(t)弱收敛于υ(t)的广义导数。

为了证明定理2,先给出如下引理。

引理2[6]如果系统

(7)

的解都满足:y1(t)→0,y2(t)→0(t→∞),则对任意常数T>0和可积函数υ(t),且υ(t)有界,有系统

(8)

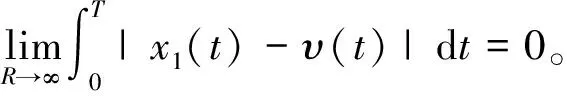
由引理2和定理1可知,定理2成立。系统(5)即为本文设计的新型HNTD,HNTD设计形式较简单,易于工程实现,且仅有R、a1、a2、b共4个设计参数,便于参数整定。利用HNTD可以同时实现对输入函数υ(t)及其一阶导数的有效估计。

2 HNTD参数整定规则

制定较为实用的设计参数整定规则,对于提升HNTD的实用价值和应用范围很有帮助。系统的开

环频域特性可以反映其响应速度和噪声抑制能力等信息,通过扫频测试[15]可以较精确地获取HNTD的频域特性。进行扫频测试仿真,分别分析设计参数R、a1、a2、b的取值变化对HNTD的频域特性带来的影响,可为这些设计参数的整定提供参考。设计参数的具体取值见表1,对应的HNTD频域特性如图2所示。通过分析图2并结合式(5)可知:增大R可以加快HNTD响应速度并提高跟踪和微分精度,但会降低噪声抑制能力,过大的R会导致跟踪和微分输出颤振;a1与R效果类似,其对跟踪效果影响较大,增大可以加快跟踪速度和提高跟踪精度,但过大会导致跟踪输出颤振;a2对微分效果影响较大,增大可以提高噪声抑制能力,但会降低响应速度;增大b可以更好地抑制噪声,但过大会增大跟踪误差。因此,对HNTD进行参数整定时,首先取b为较小值,其次选择合适的R,然后微调a1、a2来调整跟踪和微分效果,最后通过调整b获取理想的跟踪、微分和噪声抑制效果。

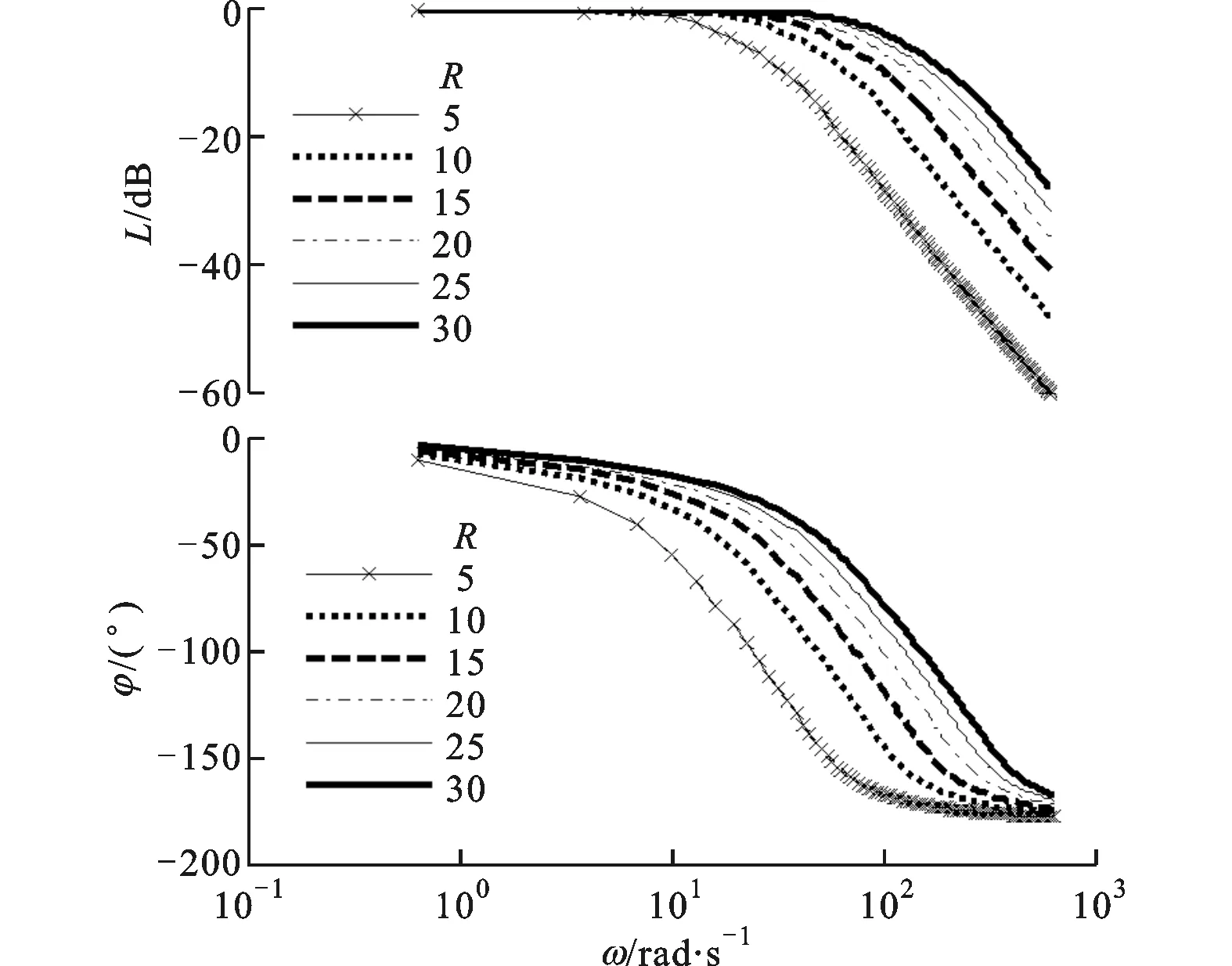
(a)R变化对HNTD频域特性的影响

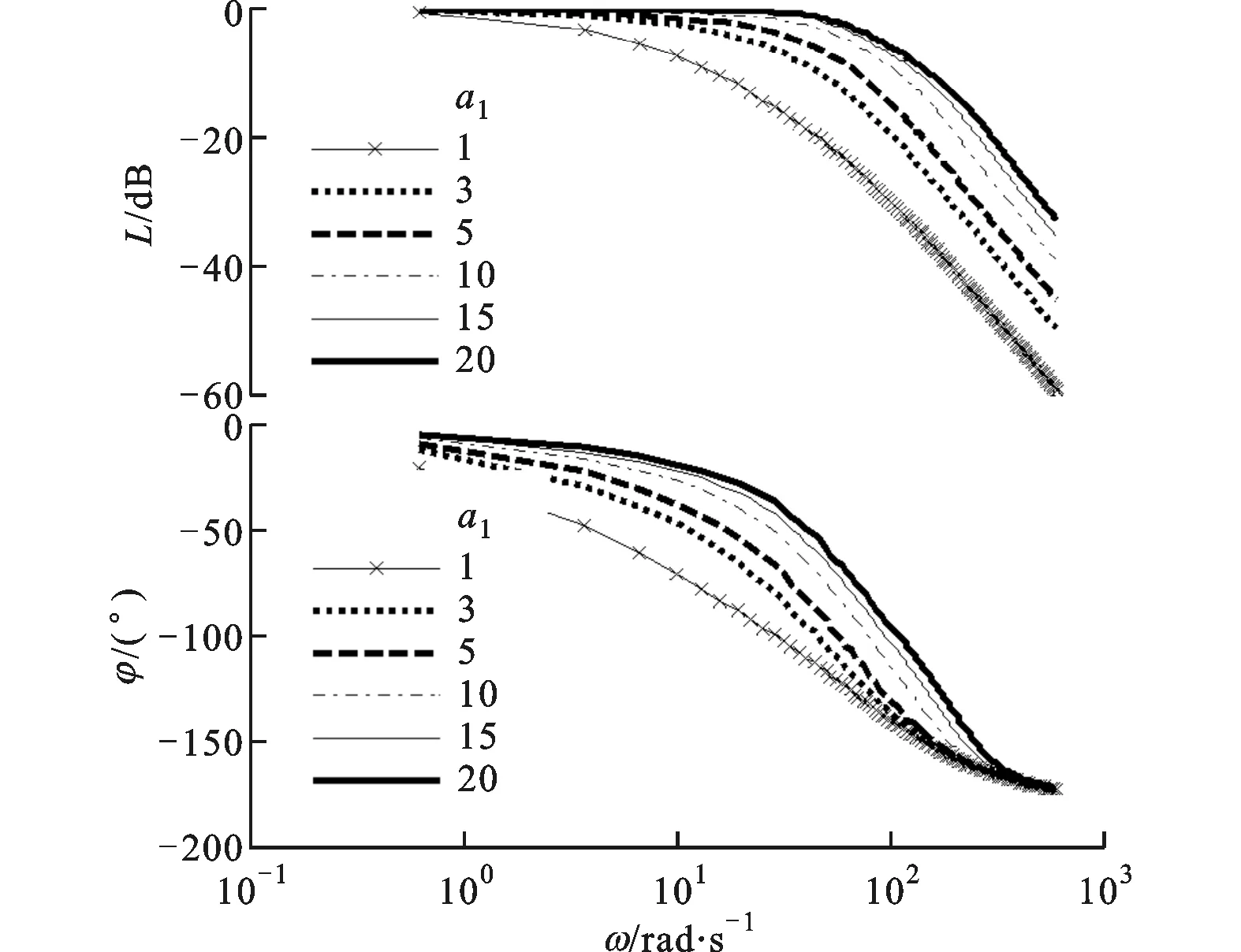
(b)a1变化对HNTD频域特性的影响

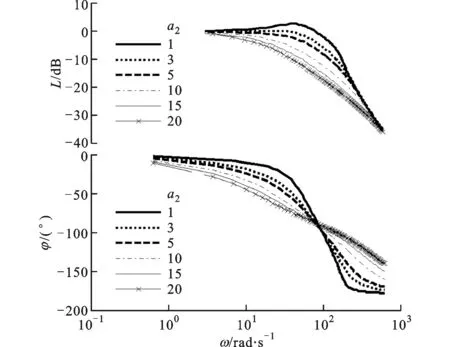
(c)a2变化对HNTD频域特性的影响

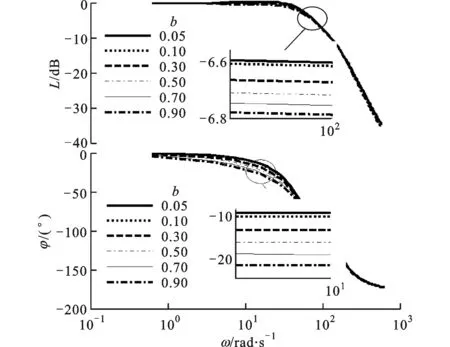
(d)b变化对HNTD频域特性的影响

可变参数取值其他参数取值R=5，10，15，20，25，30a1=15a2=4b=09a1=1，3，5，10，15，20R=20a2=4b=09a2=1，3，5，10，15，20R=20a1=15b=09b=005，01，03，05，07，09R=20a1=15a2=4

3 仿真验证

(1)对HNTD的跟踪和微分性能进行仿真验证,并与文献[6]中改进的高稳快速非线性-线性跟踪微分器(MTD)、文献[12]中改进的跟踪微分器(ITD)和文献[13]中的反正切形式跟踪微分器(ATD)进行仿真对比。输入信号为受到方差为0.1的随机噪声污染的方波信号,仿真步长取0.001 s。4种跟踪微分器设计参数取值见表2。由表2可知,本文提出的HNTD在4种跟踪微分器中设计参数相对较少,仿真结果如图3所示。由图3b可知,4种跟踪微分器的跟踪输出x1都较平滑,跟踪误差都能最终趋于0,但是HNTD跟踪速度最快,且无超调,MTD跟踪速度次之,ITD跟踪速度最慢,ATD虽有较快的跟踪速度,但存在较大的超调量。由图3c可知,HNTD微分输出x2不仅响应速度最快,而且平滑无超调,表现出对噪声良好的抑制能力;MTD也有较快的响应速度,但噪声抑制能力差,微分输出曲线存在颤振;ATD、ITD不仅微分响应速度慢,且都存在显著的输出颤振。仿真结果充分表明,在4种改进的跟踪微分器中,HNTD在响应速度、跟踪精度和噪声抑制能力方面较其他3种微分器具有一定的优势。

表2 4种跟踪微分器设计参数取值

(2)跟踪受到方差为0.1的随机噪声污染的正弦信号sin(2πt)。对比HNTD、MTD和ATD的跟踪效果,仿真步长取0.001 s。3种跟踪微分器设计参数的取值见表3。仿真结果如图4所示,可知HNTD不仅跟踪输出x1精度高、速度快,而且微分输出x2较平滑、超调量小。综合对比响应速度、滤波能力和跟踪精度等性能,HNTD较MTD、ATD有一定的优势。

(a)受到随机噪声污染的方波输入信号

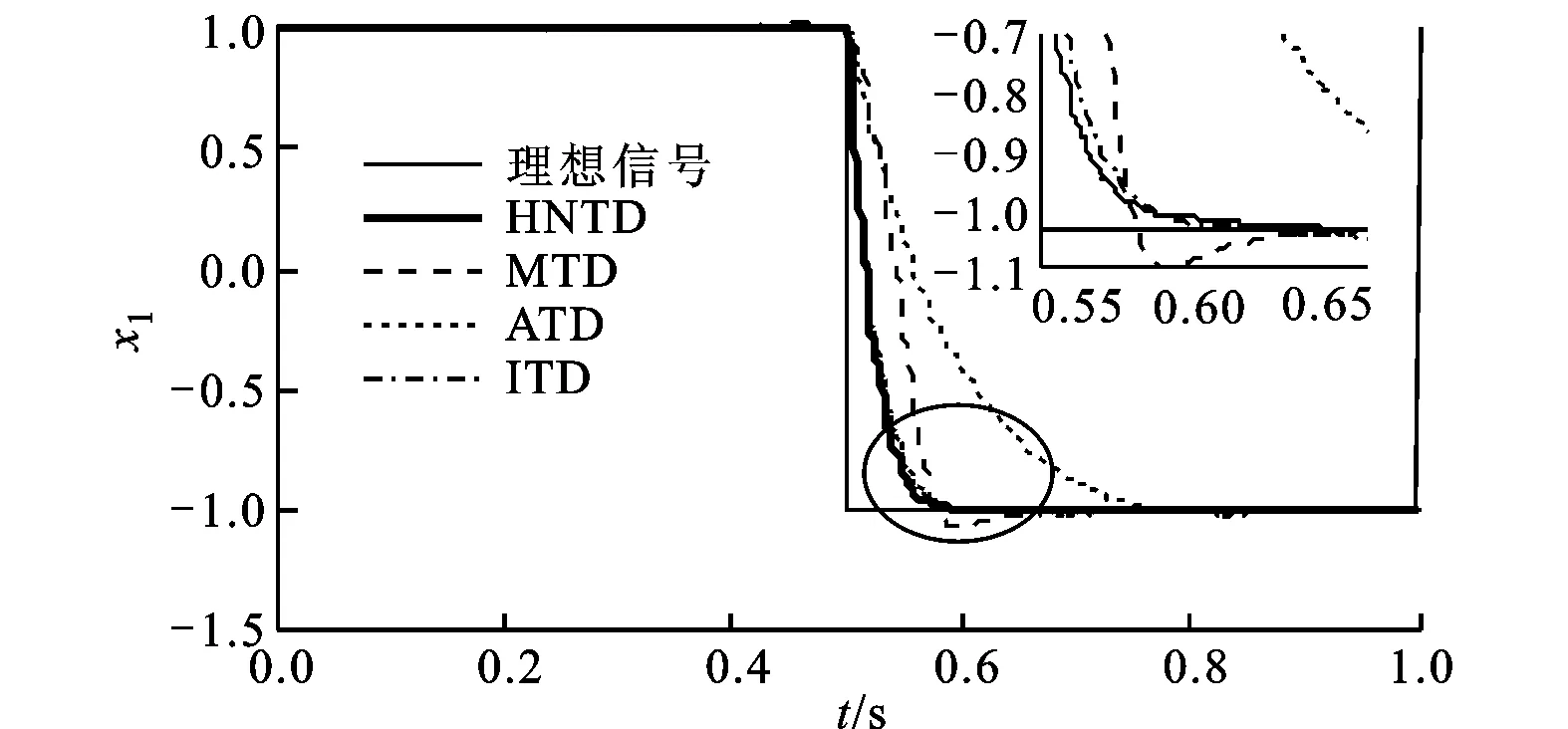
(b)跟踪效果比较

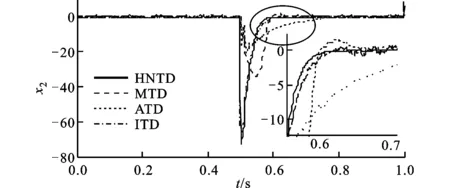
(c)微分效果比较图3 4种跟踪微分器对方波信号的跟踪效果

跟踪微分器设计参数取值HNTDR=20，a1=10，a2=1，b=09MTDR=20，a=5，b=5，m=3ATDR=20，a1=5，a2=4，f1=f2=2

4 结 论

基于双曲正弦函数和终端吸引子函数设计了一种新型HNTD。当状态远离平衡点时双曲正弦函数表现为非线性特性,当状态接近平衡点时表现为线性特性。利用这一特性保证了HNTD收敛的快速性和平滑输出,并展现了良好的滤波能力。终端吸引子函数进一步增强了HNTD对噪声的抑制能力。对参数整定规则的明确,增强了HNTD的工程实用性。仿真结果表明,HNTD不仅结构形式简单、设计参数相对较少、整定规则明确,而且在跟踪精度、响应速度和滤波能力等方面较几种改进的跟踪微分器均有一定的优势。

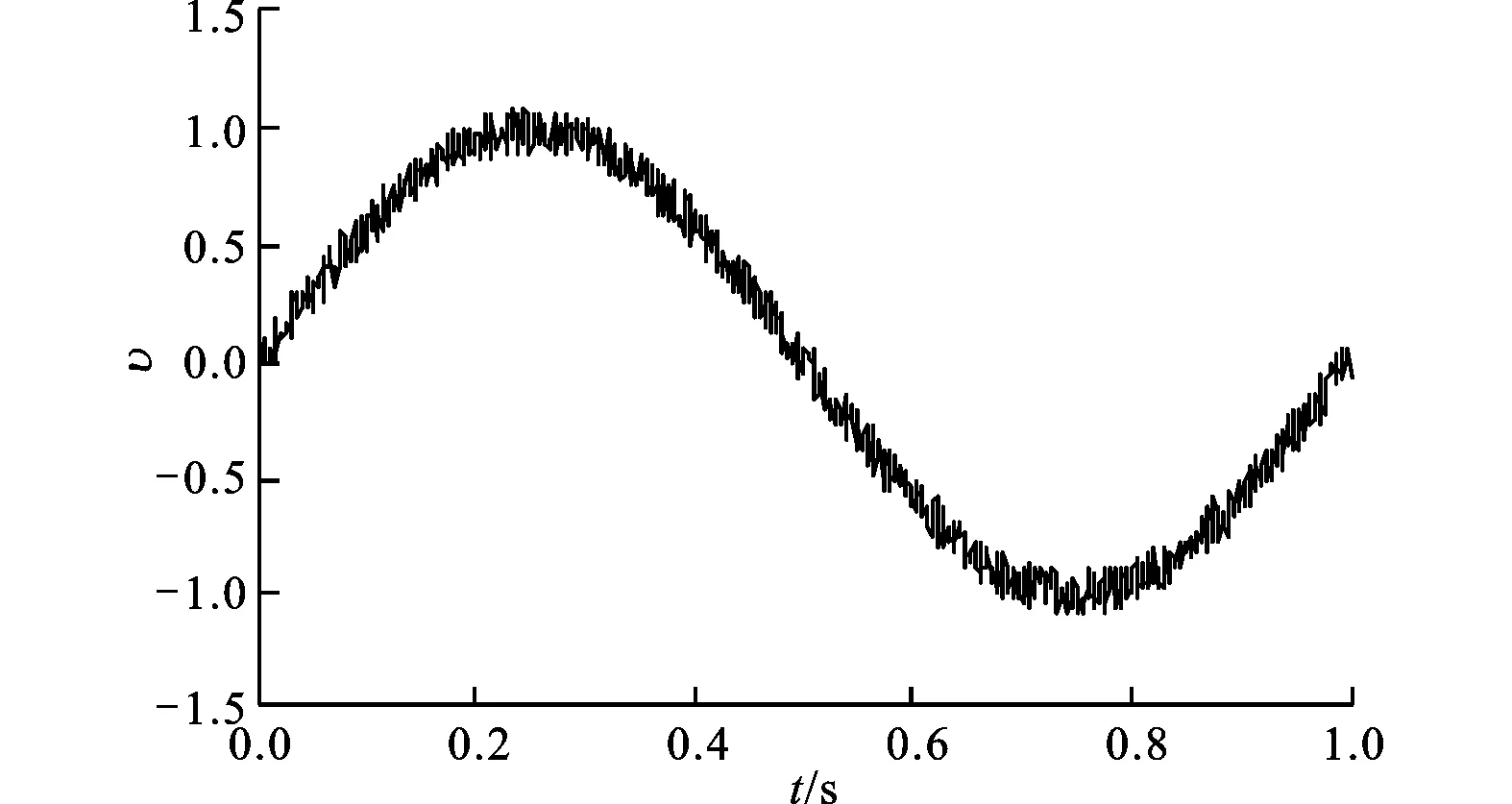
(a)受到随机噪声污染的正弦输入信号

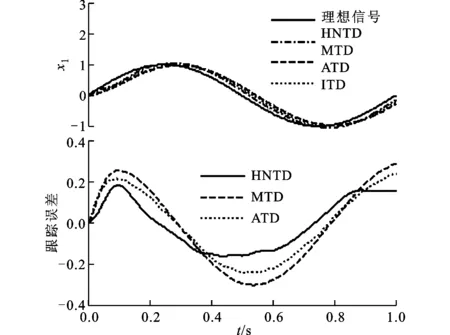
(b)跟踪效果比较

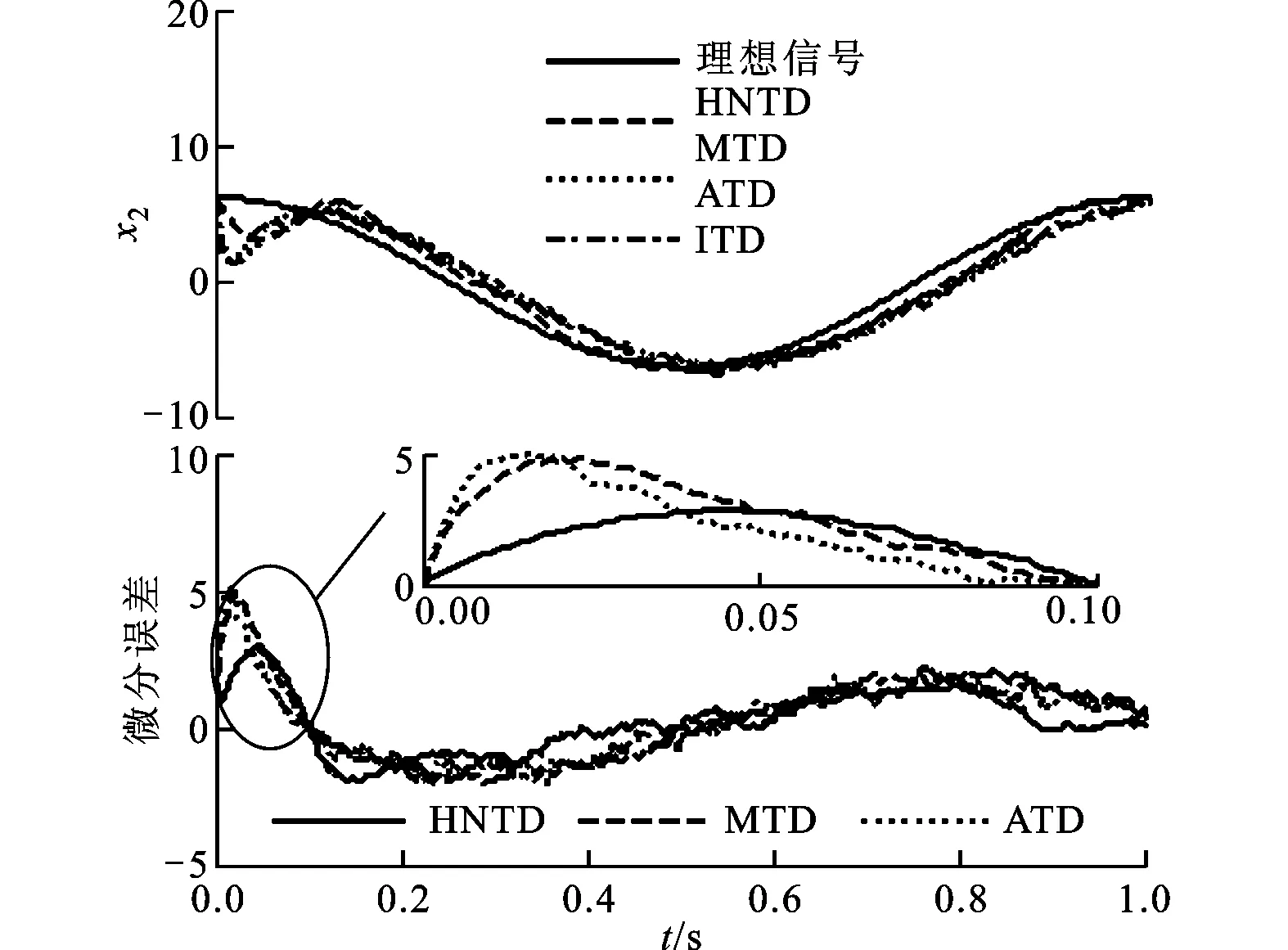
(c)微分效果比较图4 3种跟踪微分器对正弦信号的跟踪效果

[1] LEVANT A. High-order sliding modes, differentiation and output-feedback control [J]. International Journal of Control, 2003, 76(9/10): 924-941.

[2] LEVANT A. Principles of 2-sliding mode design [J]. Automatica, 2007, 43(4): 576-586.

[3] LEVANT A. Finite differences in homogeneous discontinuous control [J]. IEEE Transactions on Automatic Control, 2007, 52(7): 1208-1217.

[4] 蒲明, 吴庆宪, 姜长生, 等. 高阶滑模微分器的分析与改进 [J]. 控制与决策, 2011, 26(8): 1136-1140. PU Ming, WU Qingxian, JIANG Changsheng, et al. Analysis and improvement of higher-order sliding mode differentiator [J]. Control and Decision, 2011, 26(8): 1136-1140.

[5] 蒲明, 吴庆宪, 姜长生, 等. 快速高阶滑模微分器 [J]. 控制与决策, 2012, 27(9): 1415-1420. PU Ming, WU Qingxian, JIANG Changsheng, et al. Fast higher-order sliding mode differentiator [J]. Control and Decision, 2012, 27(9): 1415-1420.

[6] 韩京清, 王伟. 非线性跟踪-微分器 [J]. 系统科学与数学, 1994, 14(2): 177-183. HAN Jingqing, WANG Wei. Nonlinear tracking-differentiator [J]. Journal of Systems Science and Mathematical Sciences, 1994, 14(2): 177-183.

[7] QI Gaoyuan, CHEN Zengqiang, YUAN Zhuzhi. New tracking-differentiator design and analysis of its stability and convergence [J]. Journal of Systems Engineering and Electronics, 2004, 15(4): 780-787.

[8] FENG H, LI S J. A tracking differentiator based on Taylor expansion [J]. Applied Mathematics Letters, 2013, 26(7): 735-740.

[9] 王新华, 陈增强, 袁著祉. 全程快速非线性跟踪-微分器 [J]. 控制理论与应用, 2003, 20(6): 875-878. WANG Xinhua, CHEN Zengqiang, YUAN Zhuzhi. Nonlinear tracking-differentiator with high speed in whole course [J]. Control Theory & Applications, 2003, 20(6): 875-878.

[10]赵鹏, 姚敏立, 陆长捷, 等. 高稳快速非线性-线性跟踪微分器 [J]. 西安交通大学学报, 2011, 45(8): 43-48. ZHAO Peng, YAO Minli, LU Changjie, et al. Design of nonlinear-linear tracking differentiator with high stability and high speed [J]. Journal of Xi’an Jiaotong University, 2011, 45(8): 43-48.

[11]葛连正, 陈健, 李瑞峰. 改进的跟踪微分器设计 [J]. 吉林大学学报: 工学版, 2011, 41(5): 1439-1443. GE Lianzheng, CHEN Jian, LI Ruifeng. Design of an improved tracking differentiator [J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(5): 1439-1443.

[12]史永丽, 侯朝桢. 改进的非线性跟踪微分器设计 [J]. 控制与决策, 2008, 23(6): 647-650. SHI Yongli, HOU Chaozhen. Design of improved nonlinear tracking differentiator [J]. Control and Decision, 2008, 23(6): 647-650.

[13]董小萌, 张平. 反正切形式跟踪微分器设计及相平面分析 [J]. 控制理论与应用, 2010, 27(4): 533-537.DONGXiaomeng,ZHANGPing.Designandphaseplaneanalysisofanarctangent-basedtrackingdifferentiator[J].ControlTheory&Applications, 2010, 27(4): 533-537.

[14]陆启韶. 常微分方程的定性方法和分叉 [M]. 北京: 北京航空航天大学出版社, 2002: 182-230.

[15]王新华, 刘金琨. 微分器设计与应用-信号滤波与求导 [M]. 北京: 电子工业出版社, 2010: 53-106.

(编辑 赵炜)

Design of A Hyperbolic-Sine-Based Nonlinear Tracking Differentiator

BU Xiangwei,WU Xiaoyan,ZHANG Rui,ZHU Fujing

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

A new hyperbolic-sine-based nonlinear tracking differentiator (HNTD) is presented to improve the performance of traditional tracking differentiators that are complicated, difficult to regulate parameters, and hard to restrain noises. The tracking function of HNTD is constructed by introducing a terminal attractor function and a hyperbolic sine function, and its global uniform asymptotical stability is proved. Then, the parameter regulating principle is obtained by analyzing the effects of parameters changes on frequency domain characteristics. The use of the hyperbolic sine function ensures the convergence speed of HNTD’s states and eliminates chattering near the trimmed point. An excellent noise constraint performance is achieved by using the terminal attractor function. Simulation results show that the parameters of HNTD are easy to regulate, and the performance of HNTD is better than that of the traditional tracking differentiators in tracking speed and filtering.

nonlinear tracking differentiator; terminal attractor function; hyperbolic sine function; noise restraint

2014-04-17。

卜祥伟(1987—),男,博士生;吴晓燕(通信作者),女,教授,博士生导师。

航空科学基金资助项目(20130196004);陕西省自然科学基础研究计划资助项目(2012JM8020)。

时间:2014-10-23

10.7652/xjtuxb201501018

TP273

A

0253-987X(2015)01-0107-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141023.1634.001.html