卫星通信系统双向中继转发自干扰消除算法

唐成凯,廉保旺,张玲玲

(1.西北工业大学电子信息学院,710072,西安;2.西北工业大学航海学院,710072,西安)



卫星通信系统双向中继转发自干扰消除算法

唐成凯1,廉保旺1,张玲玲2

(1.西北工业大学电子信息学院,710072,西安;2.西北工业大学航海学院,710072,西安)

针对卫星通信系统频谱资源日益紧张、邻带干扰难以消除的问题,提出了一种双向中继转发自干扰消除算法。该算法对地面通信站上、下行频带采用相同的匹配频带,并通过中继卫星进行放大转发实现频率复用;利用地面通信站对自身发射信号已知的特点,通过延时寄存器对自身发射信号进行多抽头采样,然后根据各抽头采样对接收信号的干扰影响,对抽头采样进行加权处理并赋予不同权重,以减小自身发射信号的干扰;最后采用网络栅格方案对剩余信号进行解码。该算法可依据不同的信号调制方式和码延时长度动态调整网络栅格的大小,在保证误码率的情况下,能有效降低解码复杂度,从而缩短卫星通信链路的建立时间。仿真结果表明,与基于全网络栅格方案的双向中继转发通信相比,在16APSK调制下误码率为10-3时,信噪比为27 dB,但解码复杂度只相当于全网络栅格方案的10%。

卫星通信;双向中继转发;自干扰消除;频率复用;网络栅格

双向中继转发卫星通信可以复用频谱资源[1],提高频谱利用率。但是,卫星信道的非线性特性和地面通信站发射信号的异步性会使系统性能大幅度下降[2],因此寻找一种能在异步条件下,快速建立卫星通信链路并完成数据解调的双向中继转发卫星通信方法就成为研究的热点。

将发射功率进行功率回退处理,使星载功率放大器工作在线性区域,可使非线性干扰大幅下降。文献[3]在此基础上提出了一种双向频率复用通信技术,该技术主要针对BPSK调制方式和QPSK调制方式等均等幅度信号,但对于16APSK调制方式、16QAM调制方式和32APSK调制方式等多幅度多分量信号并不适用。文献[4]提出了一种多用户同频传输的算法,该算法通过对不同用户的信号进行分时传输,从而实现频率复用,但该算法在单一时间段内,每条链路上所传输的信号均为单用户信号,因而当频率的利用率达到饱和时,就不能再增加传输信号容量,所以该算法不适合作为主要的通信手段。文献[5-6]提出了2种双用户协作卫星通信算法,这些算法均假设2个地面站的传输信号在到达中继卫星时为同步信号,但在实际的卫星协作通信中,由于传输距离和空间环境的不同,信号同步是非常难以实现的。文献[7]提出了一种基于栅格查找算法的中继转发通信技术,但如果采用诸如16APSK等高阶调制信号,栅格大小会呈现指数增长并消耗过长的训练时间,大大降低了卫星通信的实际效率。

针对以上问题,在不进行卫星预失真处理和地面通信站盲均衡处理的条件下,本文提出了一种可用于卫星通信信号非同步条件下的自干扰消除双向中继转发通信算法。该算法利用自身发射信号已知的特点,通过延时寄存器将自身发射信号从所接收到的混合信号中消除,并利用网络栅格对剩余信号进行解码从而得到传输数据。在保证误码率的前提下,算法的计算复杂度和所需计算时间均能有效减小,从而提高了卫星通信的总容量。

1 系统模型

在双向中继转发卫星通信系统中,假设地面通信站B1和B2需要进行相互通信。它们发射信号的载波频率设为f1并将该载波称为上行链路。由于中继卫星没有采用码分多址(CDMA)和频分多址(FDMA)等复用技术,所以中继卫星将地面通信站B1和B2发射信号所组成的混合信号进行变频放大转发。该混合信号通过载波频率为f2的星地链路转发给地面通信站B1和B2,并将该载波称为下行链路。此时地面通信站B1和B2所接收到的信号均为包含自身发射信号的混合信号,其中自身所发射的信号相对自身的接收机来说为强干扰信号。

由于地面通信站B1和B2的结构相同,所以以地面通信站B1为例给出系统的通信模型,并利用采样率为8的离散数字模型来代替模拟信号模型。在系统中,假设地面通信站B1和B2所需要发射的信号为M1和M2,上采样后的离散信号为S1和S2,地面通信站B1和B2的功率回退量值为α1和α2,2个地面通信站之间的信号码时延为τ,地面通信站B1和B2的发射信号为U1和U2,卫星信道噪声N采用高斯白噪声,地面通信站B1和B2所接收到的混合信号为V,地面通信站B1的判决输出信号为R。在卫星信道上,由于Saleh信道为目前最接近真实卫星信道的信道模型并具有明显的非线性特性[8],所以在本系统中采用Saleh信道来模拟真实的卫星信道[9]。系统结构如图1所示。

图1 系统模型

1.1 上行链路

为了追求最大化的频谱利用率,假设地面通信站B1和B2所发射信号的周期为Ts,从而得到符号速率为Rs=1/Ts[10]。整形滤波用于消除传输信号的邻带干扰,在信号发射前,假设所有的发射机都进行发射信号功率归一化处理。其次,由于传播延时和本地时钟不一致,所以很难在中继卫星上实现同步接收[11],并且卫星也不具有星上处理功能,所以在其中一路信号上加上延时模块,用于描述2个信号之间的延时τ。τ的取值范围为0≤τ≤Ts/2[12]。当τ为0时,系统为同步系统,此时由于没有码延时,所以码间干扰会比较小;当τ为Ts/2时,系统为非同步系统,此时由于码延时的关系,码间干扰将达到最大值。

由于星载功率放大器的非线性特性,所以在系统模型中,采用功率回退因子α1和α2来描述地面通信站B1和B2接收机功率回退(input power backoff, IBO)的量值[13]。

在系统模型中,假设离散信号X1(n)和X2(n)经过信号调制和上采样后得到离散信号s1(k)和s2(k),n为下采样时刻,将该离散信号通过整形滤波器和延时模块可以得到2个地面通信站的发送信号u1(n)和u2(n),即

(1)

(2)

式中:h为整形滤波器;L为滤波器的时延;l为时延的采样时刻;k为当前采样时刻。

通过功率回退处理将卫星的发射功率控制在饱和区域或线性区域。例如,功率回退0 dB表示星载功率放大器工作在饱和区域,功率回退为-3 dB表明功率放大器的输入信号功率有3 dB的功率衰减,但是否工作在线性区域,主要取决于接收功率和叠加的信号数量[14]。为了简化模型,假设上行链路中发射功率远远大于噪声,从而忽略上行链路的噪声影响[15-16]。

1.2 下行链路

在下行链路中,为了达到频率复用的目的,中继卫星所转发的信号为包含所有上行链路信号的混合信号,对地面通信站B1来讲,需要从混合信号中解调出地面通信站B2所发射的信号M2。从图1中可以得到如下的混合信号表达式

v(k)=g(u1(k)+u2(k))+Nk

(3)

式中:k为采样时刻;g(·)为Saleh信道模型函数;Nk为采样时刻k的背景噪声。此时地面接收站B1所接收到的混合信号v(k)需要经过匹配滤波器来限制频谱并消除邻带干扰,然后进行下采样处理[15]。最终得到离散形式下的接收混合信号r(n),即

u2(8n-l))h(l)+n1(8n-l)h(l)=

(4)

式中:h为匹配滤波器,该滤波器采用和整形滤波器相同的时延和结构;w(n)为下采样后的噪声。

2 自干扰消除算法

图2 自干扰消除算法结构图

自干扰消除算法中寄存器的抽头系数是由编码延时所决定的。当地面通信站的信号为同步信号时,自干扰主要来源于当前采样时刻所对应的自身发射信号,所以抽头个数可以简化为1;当地面通信站的信号具有最大延时τ=Ts/2时,自干扰主要来源于当前采样时刻以及前后采样时刻所对应的自身信号矢量。所以,抽头数大于4时,性能变化不大,接近理想情况。为了保证数据M1分布在采样时刻n的两边,对信号进行延时处理,自干扰消除的输出信号为

(5)

ci(n+1)=ci(n)+ηe*(n)X1(n-i)

(6)

式中:η为更新步长,如果步长取值较大,抽头因子会很快收敛但误差波动较大,如果步长取值较小,抽头因子收敛较慢但误差波动较小,所以更新步长η的取值需要进行折中,本文中选取η=10-3。

当完成自干扰消除后,利用网络栅格对剩余信号y进行解码,首先将剩余信号y改为如下的网络栅格模型

y(n)=μ(X1(n-L1),…,X1(n+L2),X2(n))+Zn

(7)

式中:L1表示当前采样时刻所对应的前向延时;L2表示当前采样时刻所对应的后向延时;Zn表示当前采样时刻的噪声和未被包含在模型中的其他自身信号干扰;μ(·)为网络栅格函数。因为自干扰消除算法已经将大部分自身发射信号所产生的干扰消除,所以将式(7)模型中的自干扰部分排除以减小计算量,简化后的模型如下

y(n)=μ(X2(n))+Zn

(8)

由于在自信号消除中,为了减小计算量,采用的是线性消除函数,所以自信号的非线性干扰还残存于y中。因此,在式(8)模型中,对地面通信站B1来说,Zn包括了M1的非线性干扰和星地链路的噪声。在实际仿真中,发现式(8)的模型误差较大不能满足实际的需求,所以加入2个与当前采样时刻发射顺序关系最近的自身发射信号采样来减小自身信号的非线性干扰。此时剩余信号y(n)改为如下的模型

y(n)=μ(X1(n),X1(n+1),X2(n))+Zn

(9)

在该模型中,2个自干扰信号X1(n)和X1(n+1)被加入来减小自干扰非线性干扰对最终判决的影响。采用网络栅格中元素与剩余信号之间几何距离最小的元素所对应的数据X2作为判决输出,查找运算如下

μ(X1(n),X1(n+1),X2(n))|)

(10)

3 仿真结果与分析

在卫星通信DVB-S2标准中,16APSK调制方式的性能最好,其具有12个相位分量和2个幅度分量,可以包含现有的所有调制方式特点,所以在本文的所有仿真中均采用16APSK调制方式。

在仿真中,本文采用的上行载波频率为12 GHz,下行载波频率为14 GHz,传输带宽为200 MHz。整形滤波器和匹配滤波器均采用升余弦滚降滤波器,滤波器的延时为8个编码周期,滚降系数为0.25。在通信传输阶段,信号M1和M2的数量均为5×106个。将本文提出的自干扰消除算法与文献[7]提出的全网络栅格查找算法进行比较。文献[7]算法利用1～5个自身发射信号与一个需解调信号组成解码栅格查找表。该算法的性能主要依赖于2个因素,一个是栅格的大小;另一个是2个地面通信站所发射信号之间的码延时。设定文献[7]的算法1的栅格长度为2(1个自身发射信号和1个所需解调信号);设定文献[7]算法2的栅格长度为5(4个自身发射信号和1个所需解调信号)。

由于中继卫星只是将所接收到的混合信号进行放大转发,所以当2个地面站的发射功率不一样时,发射功率大的地面站所接收到的混合信号中,自干扰信号干扰较大,需解调信号功率较小,导致误码率较高。为了避免这种情况,在本文中,设定地面站的发射功率相同,功率回退量值α1=α2。

本文算法1采用式(8)模型,主要用于延时τ=0的条件下仿真,此时栅格元素总数目为16;本文算法2采用式(9)模型,主要用于延时τ=Ts/2的条件下仿真,此时栅格元素总数目为163。

在仿真分析中,将以信噪比、功率回退和误码率对算法性能进行分析,并假设在所有下行链路的增益均为1。

3.1 延时τ=0条件下误码率仿真

首先在延时τ=0的条件下进行仿真,这是一种理想情况,在实际的卫星通信中很难实现这种情况。此时,本文算法1和本文算法2的仿真结果十分接近,但在16APSK调制方式下,本文算法1的网络栅格总数远远小于本文算法2。在不同的功率回退和信噪比条件下,将本文算法1与文献[7]算法1进行比较,得到的误码率性能如图3所示。

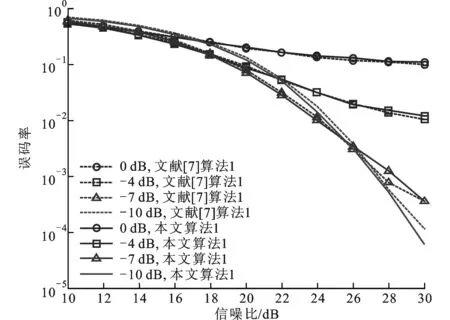
图3 τ=0时不同功率回退值下2种算法的误码率曲线

从图3中可以看出,功率回退对误码率的影响较大。功率回退较大时,星地链路处于线性传播区域,此时非线性干扰较小,本文算法1和文献[7]算法1都可以有效消除线性干扰,误码率较低。但功率回退又会导致发射功率变小,从而使信噪比变差,误码率提高。这和之前的理论分析是完全一样的,所以需要在功率回退和非线性干扰之间寻找一个平衡点。在图3中,不同的功率回退在不同信噪比下会对误码率产生不同的影响。当功率回退为-3 dB、误码率为10-2时,最优信噪比为24 dB;但当功率回退为-10 dB、误码率为10-2时,最优信噪比为25 dB。文献[7]算法1所在同步条件下与本文算法1的误码性能相当接近,但本文算法1的计算量要远远小于文献[7]算法1。

3.2 延时τ=Ts/2条件下误码率仿真

当延时τ=Ts/2时,码间干扰最大,误码率最高。在此条件下,由于采样时刻是由M2所决定,所以地面通信站T1的自身信号M1会产生非常大的码间干扰。文献[7]算法1和本文算法1的误码率曲线如图4所示。

图4 τ=Ts/2时不同功率回退下2种算法的误码率曲线

从图4中可以看出,在异步条件下文献[7]算法1无论如何增加信噪比,都不能有效降低误码率。所以,文献[7]提出的算法2需要确保栅格长度大于等于5,在16APSK调制下,总的栅格元素数量会超过165个,这就导致网络栅格建立所需的时间过长,不利于实际的卫星通信。采用本文算法1(即μ函数仅包含离散信号X2(n)时),无论如何增加信噪比,误码率都有一个误码率底线,这是由于μ函数模型不能覆盖其中一部分自身信号M1的干扰,而自干扰消除算法只能消除自身信息数据M1的线性干扰,而非线性干扰需要通过功率回退和建立网络栅格的方法进行二次消除。因此,本文在相同的非同步条件下,对本文算法2和文献[7]算法2进行仿真,仿真结果如图5所示。

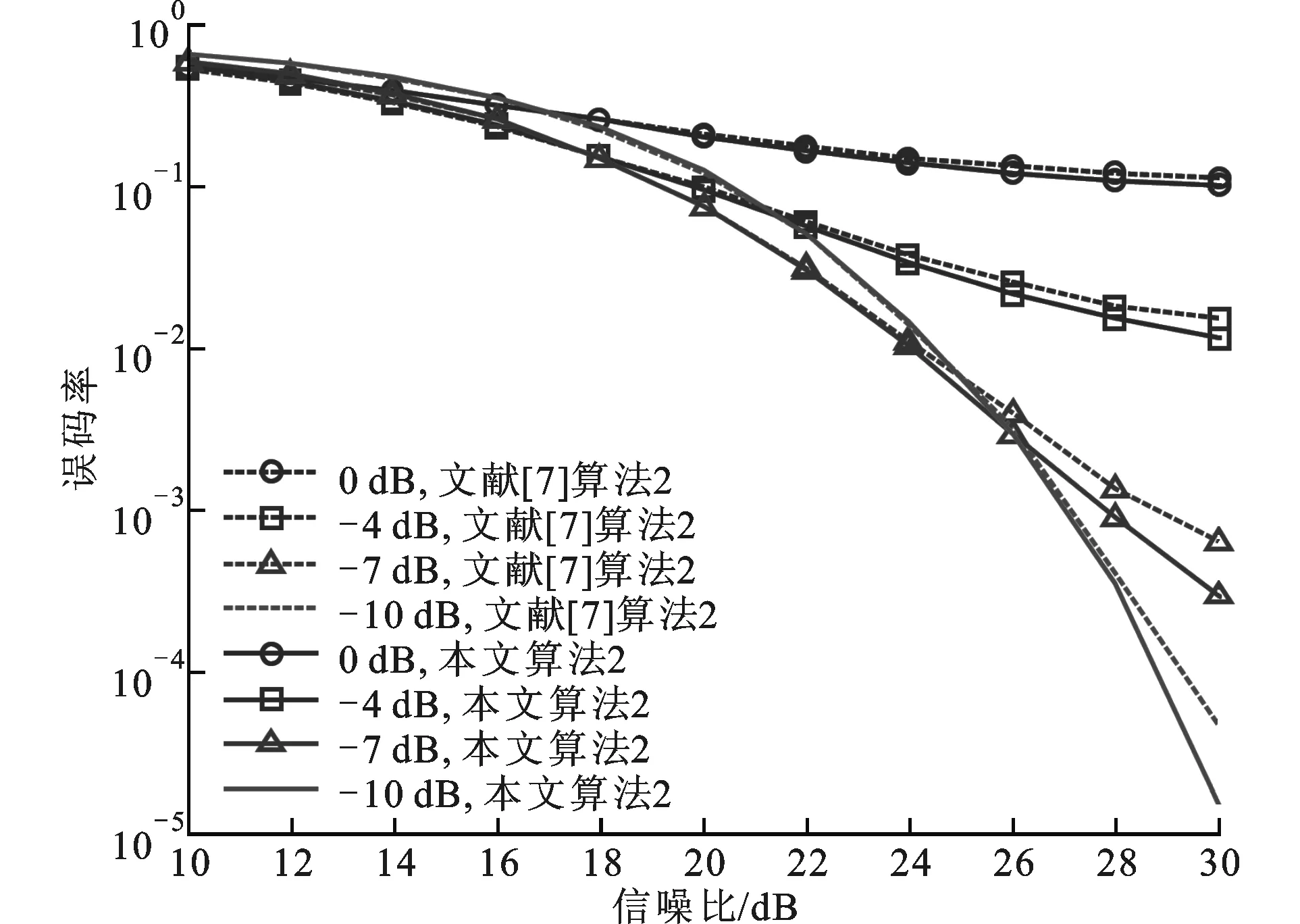
图5 式(9)模型和文献[7]算法在异步条件下的误码率曲线

从图5中可以看出,当功率回退为-7 dB、误码率为10-2时,信噪比为24.2 dB,与图4相同条件下的信噪比相比,具有3.8 dB的提升,当功率回退为-10 dB、误码率为10-3时,信噪比为27.2 dB,与同步条件下的信噪比十分接近。

3.3 计算复杂度分析

由于在双向中继转发卫星通信中,地面通信站所发射的信号在到达中继卫星时,很难保持同步,因此在计算复杂度时,不考虑τ=0这种理想情况。对本文算法与文献[7]算法进行计算复杂度比较,结果如表1所示。其中假设平均每个栅格元素所需的训练符号数为50。

表1 2种算法的计算复杂度比较

从表1中可以看出,本文算法在总的元素数和训练阶段所需符号数上都远远小于文献[7]算法,因此本文算法可以更加快速有效地完成卫星通信的建立和信息传输。

4 总 结

本文提出了一种双向卫星中继转发自干扰消除算法,解决了双向卫星通信中由于自干扰强度大所造成的误码率较高、卫星通信链路建立时间较长的问题。在不进行星载预失真处理和地面通信盲均衡处理的前提下,通过延时寄存器对自身信号进行延时抽头构建自干扰消除算法,以消减自身信号干扰,并使用网络栅格算法对剩余信号进行解码,降低了误码率。仿真结果表明,在相同误码率条件下,本文算法的复杂度优于全网络栅格算法,在16APSK调制方式下,本文算法的复杂度仅为全网络栅格算法的10%,可充分满足卫星通信链路建立时间的需求。

[1] MORIO T, TAKASHI S, HIDEKI T. Scintillation model of laser beam propagation in satellite-to-ground bidirectional atmospheric channels [J]. Acta Astronautica, 2012, 80(1): 58-64.

[2] SIDDALL G R, FOWLER G A, BEANLANDS B D, et al. “Seacycler”: a deep ocean profiler with full mooring two-way satellite communication [C]∥Proceedings of the International Offshore and Polar Engineering Conference. Piscataway, NJ, USA: IEEE, 2012: 493-501.

[3] HU Zhengqun, AI Guoxiang, ZHANG Lirong. A control system in satellite navigation and communication terminal [J]. Applied Mechanics and Materials, 2014, 513(1): 2888-2892.

[4] MORIO T, TAKASHI S, WERNER K. Overview of the laser communication system for the NICT optical ground station and laser communication experiments on ground-to-satellite links [J]. Journal of the National Institute of Information and Communications Technology, 2012, 59(1): 53-75.

[5] SKULIMOWSKI A M J. Web-based learning in remote areas: an evaluation of learning goals, scenarios and bidirectional satellite internet implementation [C]∥Proceedings of 12th International Conference on Web-based Learning. Piscataway, NJ, USA: IEEE, 2013: 50-60.

[6] YANG Zhenchao, WARNICK K F. A planar passive dual band array feed antenna for Ku band satellite communication terminals [C]∥Proceedings of IEEE Antennas and Propagation Society. Piscataway, NJ, USA: IEEE, 2012: 1-5.

[7] XU Chenguang, JOHN P, WILSON S G. Achievable information rates for nonlinear satellite channels in unidirectional and bidirectional relaying [C]∥Proceedings of IEEE Latin-America Conference on Communications. Piscataway, NJ, USA: IEEE, 2012: 1-4.

[8] PARK J, HA Y, CHUNG W. Reduced complexity MLSD equalizers based on bidirectional DFEs [J]. IEICE Transactions on Communications, 2012, 95(11): 3432-3438.

[9] ARTI M K, BHATNAGAR M R. Two-way mobile satellite relaying: a beamforming and combining based approach [J]. IEEE Communications Letters, 2014, 18(7): 1187-1190.

[10]TANG Liwen, LI Xiaojiang, LI Yiyong. Design and implementation of object monitoring and management system for satellite location [J]. Applied Mechanics and Materials, 2013, 385(1): 1531-1536.

[11]WILLIAM M, STEVEN A L, KIRK F, et al. Optical space-time division multiple access [J]. Journal of Lightwave Technology, 2012, 30(11): 1771-1785.

[12]FUJIEDA M, PIESTER D, GOTOH T, et al. Carrier-phase two-way satellite frequency transfer over a very long baseline [J]. Metrologia, 2014, 51(3): 253-262.

[13]THOTAHEWA K M S, KHAN J Y, YUCE M R. Power efficient ultra wide band based wireless body area networks with narrowband feedback path [J]. IEEE Transactions on Mobile Computing, 2014, 13(8): 1829-1842.

[14]LEONENKO G, LOS S O, NORTH P R J. Statistical distances and their applications to biophysical parameter estimation: information measures, m-estimates, and minimum contrast methods [J]. Remote Sensing, 2013, 5(3): 1355-1388.

[15]赵建伟, 贾维敏, 姚敏立. 移动卫星通信系统组合姿态估计算法 [J]. 西安交通大学学报, 2014, 48(8): 1-6. ZHAO Jianwei, JIA Weimin, YAO Minli. An estimation algorithm with integrated attitudes for mobile satellite communication system [J]. Journal of Xi’an Jiaotong University, 2014, 48(8): 1-6.

[16]齐巍, 陆明泉, 李强. 高动态测量系统中的自适应信号成形滤波器设计 [J]. 西安交通大学学报, 2013, 47(6): 124-129. QI Wei, LU Mingquan, LI Qiang. Design of an adaptive signal shaping filter in high dynamic measurement systems [J]. Journal of Xi’an Jiaotong University, 2013, 47(6): 124-129.

(编辑 刘杨)

An Algorithm to Eliminate Self-Interference of Bidirectional Relaying for Satellite Communication Systems

TANG Chengkai1,LIAN Baowang1,ZHANG Lingling2

(1. School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710072, China; 2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

An algorithm to eliminate self-interference of bidirectional relaying for satellite communication system is proposed to deal with the problem that the spectrum resource strain is increasing and adjacent band interference is hard to remove in satellite communication systems. Both the uplink and downlink transmission in grand stations occupy the common matching band and the relaying satellite plays the role of amplification and forwarding to achieve frequency reuse. Since the self-transmitted signal is known to certain ground terminal, the interference of its emission signal can be reduced by using the relay register to multitap sampling of itself transmitted signal, and calculating a weighted sum of the samples with the weights determined from interference of the multitap samples to received signal. The symbol is recovered from the residual signal by network grille. The algorithm dynamically adjusts the size of grille according the signal modulation and code delay length. The proposed algorithm can effectively reduce the decoding complexity, and shorten the satellite communication link establishment time, while the bit error rate is ensured. Simulation results and comparisons with the full network grille algorithm show that when the modulation is 16APSK the SNR are 27 dB and the bit error ratio is 10-3for both methods but the decoding complexity of the proposed method is only 10% of that of the full network grille algorithm.

satellite communication; bidirectional relaying; self-interference cancellation; frequency reuse; network grille

2014-06-04。

唐成凯(1985—),男,博士生;廉保旺(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61301094);西北工业大学研究生创业种子基金资助项目(Z2012097)。

时间:2014-10-31

10.7652/xjtuxb201502013

TN91

A

0253-987X(2015)02-0074-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1642.009.html