基于双加速度计的静态角度检测与误差分析

秦晓丽，谢新武，杨 健，孙秋明，倪爱娟，田 丰

·研究与设计·

基于双加速度计的静态角度检测与误差分析

秦晓丽，谢新武，杨 健，孙秋明，倪爱娟，田 丰

目的：对骨折固定复位训练模拟人的骨折断面位移及角度检测进行研究，解决这一实现模拟人虚实交互的关键和难点。方法：采用微电子机械系统（micro-electro-mechanical-systems，MEMS）的加速度计对骨折断面角度位移量进行静态检测，通过对骨折断面的三维欧拉坐标系建模，推导出静态角度检测的双加速度计二维联合检测方法，并进行了多倾角姿态下的不同角度测量实验。由于该方法存在测量盲区，对可能存在较大误差的测量姿态进行了误差的特性实验，最后对测量结果进行了误差分析。结果：该方法能够有效测量静态角度，除去在盲区的近水平状态，总体测量均方误差为（2.240 3±1.027 2）°，平均误差为（1.809 4±0.895 0）°。根据三维坐标数据的单位正交关系设计的优化算法对多组数据进行计算，得到平均误差可以达到（0.838 78±0.740 0）°，且不受个别盲区数据影响。在待测角度为30°的情况下，误差随着测量平面与水平面夹角的增大而减小，当夹角大于5°时，误差明显下降。结论：零点标定对结果改善有明显效果，灵敏度标定对角度测量结果改善效果有限，传感器精度、信号采集精度都是误差产生的重要原因。该方法是有效的，同时，采用测量多组数据进行优化算法解算能够达到较高的精度，并能有效规避测量盲区。

加速度计；角度检测；单位正交优化；误差分析

0 引言

骨折固定与复位训练模拟人系统的关键是对看不到的“骨折病情”的检测和显示，从而能够为固定与复位操作提供正确的指引，提高模拟训练效果。骨折的断面两端相对移位可分为分离移位、缩短移位、侧方移位、旋转移位、成角移位等[1]。对旋转、成角移位等角度量的检测，受限于模拟人肢体体积、骨骼和肌肉等软组织材料性能的差异等，难以采用常见的角度测量手段，是“骨折”各种移位检测的难点。前期研究发现采用微电子机械系统（micro-electro-mechanical-systems，MEMS）技术的3轴加速度计可满足小空间内部安装等要求，能够用于模拟骨折的检测，初步的研究可实现简单的测量，但是精度、稳定性、适用性等方面还有很多不足。

相关的研究集中在人体运动检测方面，由于各种运动捕捉系统价格昂贵且受空间地点限制，不适合对人体运动的日常监测，研究低成本、小体积、高精度、可长时间不受地点限制地测量人体运动的装置是一个热点。A T M Willemsen等[2]使用了含有8个加速度传感器的2个金属条来测量一个关节的角度。A Heyn等[3]实验证明可以使用由8个加速度传感器和2个陀螺仪组成的系统来测量膝关节的角度。H Dejnabadi[4]提出了一种新颖的由多个加速度传感器和陀螺仪组合的量测关节弯曲角度的方法，采用虚拟传感器的解决方案。LIU T等[5-6]使用3D加速度传感器来获取人体关节角度，提出了在人行走过程中着地的中间状态下使用加速度计数据对陀螺仪角度积分进行校正，从而提高陀螺仪测量动态角度精度的方法。H J Luinge等[7]采用3D加速度计测量人体躯干的倾斜角，并指出采用加速度计能在静态和准静态条件下进行倾斜角测量。J Favre等[8-9]参照生物力学学会的人体各节段坐标体系给出了膝关节3D角度外展、内收、屈曲的定义，并采用加速度计对膝关节的外展、内收、屈曲等角度进行了测量和标定。在角度的计算方法方面，D Churchill等采用旋转矩阵（roll、pitch和yaw旋转）进行计算，J Favre等[10]采用四元数表示法进行角度积分及标定计算。

综上，动态角度通常采用陀螺仪与加速度计联合测量，而加速度计也是测量倾斜角的工具之一，但是采用2个加速度计测量2个刚体间的角度量鲜见报道。前期研究已经证明了该方法的可行性[11]。本文就针对这种现状，对采用2个3D加速度计测量角度量的方法和实验结果进行研究。

1 模型建立

1.1 骨折成角与旋转移位的坐标系旋转模型

对骨折状态下的角度量成角移位、旋转移位进行测量就必须先对其建模，建立这2个参量与坐标系旋转之间的关系。将断裂的骨骼放置于世界坐标系W（X，Y，Z）中，对断裂的两端分别建立自己的坐标系，定义为W1（X1，Y1，Z1）和W2（X2，Y2，Z2），将骨骼的长轴定义为X方向，横断面则由YZ平面来定义。通过对成角、旋转的分析与简化，可由图1、2分别表示单独成角或旋转移位的旋转模型，其中图1是成角移位模型，2个坐标系Z轴方向一致，成角移位可以由坐标系W2绕Z轴方向对W1的旋转角度表示；图2是旋转移位模型，2个坐标系X轴方向一致，旋转移位可以由坐标系W2绕X轴方向对W1的旋转角度表示。骨折的角度移位均可以由这2种移位方式组合或耦合而成，骨折端面所成的角度也可以用这2个量（α、β）来度量。

图1 骨折成角移位的坐标系旋转模型

图2 骨折旋转移位的坐标系旋转模型

推广到更一般的情况：（1）成角移位可以是x2与y1z1平面所成的角，在三维坐标系中可表示为绕y1z1平面上任意过原点直线旋转某一角度α′。（2）当成角移位与旋转移位同时存在，可以看作是先绕X轴旋转β，再绕y1z1平面上任意过原点直线旋转某一角度α′。

1.2 重力加速度与坐标系旋转的关系

由于重力加速度的存在，加速度计在任意时刻的3个方向上均存在重力分量（如图3所示），其自身坐标系与重力方向的关系可表示为重力加速度向量在坐标系的位置（ax，ay，az）：

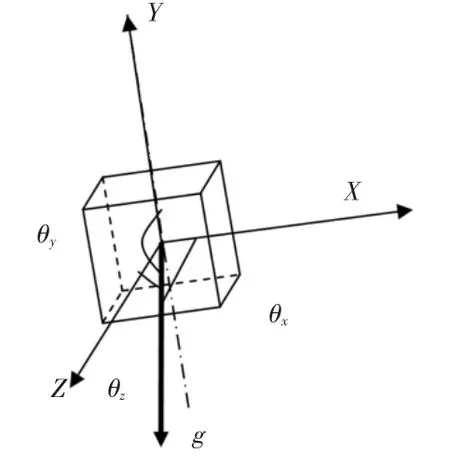
图3 3轴加速度计各方向与重力加速度方向角度的关系

静态条件下，2个加速度计的各自坐标系可以通过旋转矩阵实现旋转，而旋转前后的加速度始终为g。因而可将恒定不变的重力加速度在不同加速度计上的测量结果看作是同一矢量在不同坐标系中的坐标值，通过坐标系旋转，能将一个坐标系旋转到另一坐标系，或者是世界坐标系。通过前面对旋转移位和成角移位的建模分析，我们了解到，测量一个角度量可以通过计算旋转角来得到，而旋转角的计算，可以通过重力向量的不同坐标系表示来进行计算，重力加速度的各轴坐标值可直接测量得到。

在三维坐标系中，坐标系绕Z轴旋转θ的坐标系旋转公式为

绕X、Y轴旋转表达式与此类似。通过测量可以得到2个坐标值，从而使得式（2）只有一个未知量θ，可轻易解算出来。当我们将加速度计进行适当的安装，使得某一轴向始终一致，而2个加速度计各自代表所在刚体的方位时（如图1、2所示），采用适当的方法计算出旋转角θ，即是二者所成的角度。但是，该方法也存在一个特殊情况，即2个加速度计的测量平面都是水平的，2个加速度计的X、Y轴加速度值均为0，旋转角θ可以为任意值，上述方法无效，该状态称为测量盲点（盲区），必须进行适当处理。

2 检测实验材料与方法

3轴加速度计模块采用MMA7361作为加速度测量主芯片。MMA7361是飞思卡尔公司的一款低成本的MEMS加速度芯片，它体积小（6 mm×6 mm× 1.45 mm）、功耗低（500 μA）、灵敏度高（量程1.5g时灵敏度达0.8 V/g）、运行电压低（2.2～3.6 V）。模块集成了稳压电源（3.3 V）、简单的信号调理滤波电路，性能稳定。加速度计信号采用示波器测量，选择200 mV挡，自动测量，测量读数精度为±0.01 V。测量系统如图4所示。

图4 角度测量实验系统

2.1 传感器标定

2.1.1 零点标定

由于零点位置为Vcc/2±10%，零点偏移对结果影响较大，需首先进行零点标定。方法是变换加速度计姿态，测出X、Y、Z轴各方向静态的最大值Umax、最小值Umin，对应的加速度值分别是1g、-1g，则0g加速度为（Umax+Umin）/2。

2.1.2 灵敏度标定

芯片的标称灵敏度为（0.8±0.06）V/g，实际灵敏度的偏移也可能对结果产生影响。本文对灵敏度进行简单标定，方法是通过1g、-1g的测量，取（U1g-U-1g）/（2g）作为实际灵敏度。

2.2 角度测量实验

对0、5、15、30、45、60、75、90、175、180°等典型角度分别进行共8种典型姿态的测量（如图5所示）。

图5 测量系统8种测量姿态

2.3 近水平状态误差特征实验

从测量原理分析，如果测量的2个轴构成的平面呈水平状态时，测量到的加速度值应为0，此时是无法计算所成角度的。而在接近水平的状态下，加速度值接近0，由于各种误差的存在，使得误差在测量结果中所占比重大，计算的结果也会有较大的误差，越接近水平，误差可能越大。因而，本方法在接近水平状态下的误差特性影响到该方法的适用性。在0、1、2、3、4、5、6、7、8、9、10、12、15、18、21°等倾斜角度下测量30°成角，考察近水平状态的误差特性。

2.4 角度计算及数据处理方法

角度的计算采用单数据直接解算和多数据优化算法2种方式进行，对计算得到的角度数据、误差、均方误差等进行分析。

误差分析：误差的来源有量角器误差、传感器测量误差、示波器读数误差、计算误差等。其中，量角器精度为0.05°，对实验影响很小。传感器芯片是消费电子级的，精度有限，是误差的重要来源。而示波器读数精度是10 mV，有±0.01 V的读数误差，该项误差对结果的影响可能是除器件误差以外的重要误差来源。对测量信号的电压数据人为加入0.01 V偏差，考察计算角度结果与没有加入偏差时的差值，分别对同一敏感轴不同测量角度、同一测量角度不同敏感轴进行统计分析。

3 实验结果

3.1 传感器标定

给2个3D加速度计分别命名为加速度计1、加速度计2，各自加速度敏感轴分别为x1、y1、z1和x2、y2、z2。

传感器标定的结果见表1。

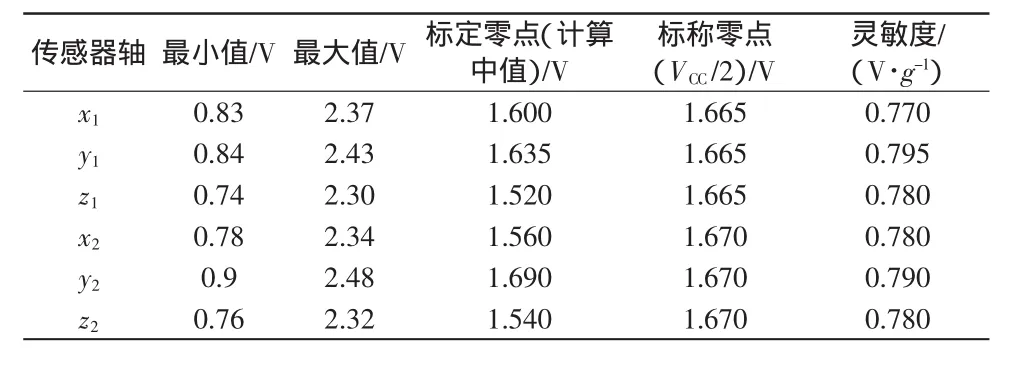
表1 加速度计标定结果

3.2 角度测量

按图5的8种姿态对列出的角度进行测量。表2列出了同一测量角度（5°）不同敏感轴的数据和计算结果，包括优化算法计算结果、误差及均方误差、除去盲区姿态1的均方误差及平均误差和其他姿态的组合计算得到的均方误差和平均误差。

表2 角度为5°测量计算结果

表3列出了所有角度的8种姿态测量误差结果，包括均方误差（RMS1）、除去姿态1的均方误差（RMS2）、各测量角度下的平均误差（平均误差1）、除去盲区姿态1的平均误差（平均误差2）以及优化算法计算的结果误差。图6对2种方法的测量误差进行了图示比较。

表3 各角度测量的误差及统计结果 （°）

3.3 近水平状态误差特性

图7给出了待测角度为30°时的近水平测量状态的误差特性，测量姿态由3.2给出。

4 讨论

4.1 测量结果讨论

从表3、图6的结果可以看出，采用直接解算方法进行单次角度测量，除了接近水平状态，其余各种姿态下的测量结果误差都不大，均方误差为1～3°，而在盲区的近水平状态（姿态1），测量均方误差为（2.240 3±1.027 2）°，平均误差为（1.809 4±0.895 0）°；而采用多组测量数据进行奇异值分解（singular value decomposition，SVD）优化计算能显著减小误差，10次计算结果平均误差为（0.838 78±0.740 0）°，小于单组数据解算的均方误差，并可有效规避测量盲区数据的影响。由此我们得出结论，采用2个加速度计，通过适当的安装和解算算法，能够较为精确地测量一个角度。采用多组数据的SVD优化算法能够使得测量精度显著提高。

从测量原理我们已知，在绝对水平状态下是无法进行测量的。接近水平的状态也会因为加速度太小而被读数误差、噪声等掩盖，产生明显的误差。由近水平状态下30°成角测量结果误差的实验（如图7所示）我们发现，测量误差的总体趋势是随着倾角增大而减小，倾角大于5°后误差就显著减小。据此我们也可以通过对近水平状态的测量误差分布曲线选择可接受的误差范围，在安装、测量过程中尽量避开测量盲区和大误差区域，减少因测量原理导致的误差乃至数据错误。

图6 各角度下2种方法的测量误差比较

4.2 误差分析

测量误差方面，误差的来源有量角器误差、传感器器件带来的误差、示波器测量误差、计算误差等。量角器精度为0.05°，理论上不会构成误差的重要来源。传感器芯片存在的误差有：零点位置±10%，已经通过零点标定进行处理；灵敏度±0.06 V/g；非线性度±1%；轴间干扰±5%。可见传感器芯片本身精度不高是误差的重要来源，本实验在进行实验前就对非常重要的零点电压进行标定，以提高精度。

为考察灵敏度标定对结果的影响，我们采用标定后的灵敏度计算静态加速度，比较与标定前的对g误差，求出误差差值Δ（a1-g）、Δ（a2-g），并使用标定后的灵敏度重新用2种方法计算角度，比较平均误差1、平均误差2以及优化算法的误差，用标定前的误差减标定后的误差，得到表4。从表4可以看出，加速度测量误差均有减小，说明标定后灵敏度准确度有所提高。同时平均误差1、平均误差2以及优化算法的误差等指标在不同测量角度下有增有减，平均误差1有减小，平均误差2以及优化算法的误差均值有所增大。说明本文的灵敏度标定对误差的改善作用有限，需要进一步深入研究。

表4 灵敏度校正对结果的影响（均值）

本实验使用的示波器读数有效数字为3位，误差为±0.01 V，对应于加速度0.012 5g，分析认为该项误差可能是结果误差的重要组成部分。对该项误差对结果的影响进行了计算分析。结果显示，不同测量角度下，人为对同一敏感轴数据加入偏差后得到的计算结果与原测量角度的差有较大差异，同一测量角度下对不同敏感轴加入误差得到的结果，误差也不相同。但是0.01 V的偏差造成的结果误差平均值也在0.3～8°（见表5），特别是在近水平姿态的测量下造成的误差很可观，而且越是接近水平，造成的误差越大（如图8所示）。原因可能是在近水平状态，真实的加速度值就非常小，0.012 5g的加速度偏差相对真实值就很大了，甚至可能完全掩盖了真实的数据，造成结果严重失真。进一步我们推断，有效提高电压测量精度，也可能大幅改善本方法的角度测量精度，尤其是接近水平状态的精度。

表5 测量误差对结果的影响（近水平10种姿态、图5中8种姿态不同敏感轴均值） （°）

5 结论

本文研究了采用2个加速度计静态角度测量的方法，进行了测量实验，并对结果进行了讨论和误差分析。由理论建模和实验结果我们可以确定，该方法是有效的，同时，采用测量多组数据进行优化算法解

（▶▶▶▶）（◀◀◀◀）算能够达到较高的精度，也能有效规避盲区影响。从误差分析我们可以得到进一步提高测量精度的方法可能有2种：（1）采用精度更高的传感器器件；（2）提高电压信号采集精度。从原理上，该方法存在固有缺陷，存在测量盲区，在水平和近水平状态下结果会严重失真。一方面我们可以通过深入研究近水平状态误差特性，并采用合适的解算方法有效规避测量盲区；另一方面，可以研究三维角度解算方法，从原理上规避该缺陷，实现高精度的测量。

Static angle detection and error analysis using a pair of 3D accelerometers

QIN Xiao-li1,XIE Xin-wu1,2,YANG Jian1,SUN Qiu-ming1,NI Ai-juan1,TIAN Feng1
(1.Institute of Medical Equipment,Academy of Military Medical Sciences,Tianjin 300161,China; 2.Pecking Union Medical College,Tsinghua University,Beijing 100084,China)

ObjectiveTo explore the detection of the fracture section displacement and angle of the simulator for fixation and restitution training.MethodsStatic detection of the angle and displacement was carried out with the accelerometers of micro-electro-mechanical-systems(MEMS).A model of fracture section was set up in 3D eulerian coordinate system to determine 2D detection method with a pair of accelerometers,and the detection was performed for different angles.The experiments were implemented for large errors in some conditions,and error analysis was executed for the detection results.ResultsFor all the conditions except the ones at the blind area,the mean square error was(2.240 3±1.027 2)°,and the mean error was(1.809 4±0.895 0)°.The optimal control algorithm was designed based on the the orthogonality relationship of the 3D accelerometers,and the mean error of all conditions in the experiment reached (0.838 78±0.740 0)°,and the measurement error was not affected by the result of blind area.When the angle was 30°,the error decrased with the angle increased between the measuring plane and the horizontal plane,and went down sharply with the angle higher than 5°.ConclusionThe detection result is significantly improved by zero-point drift compensation,and the sensitivity compensation only has little effects on improving the detection result.The accuracies of the sensor and signal acquisition may be the causes for the errors.The method for angle detection is valid,excepting for the blind area,but the optimal control algorithm based on the the orthogonality relationship of the 3D accelerometers can be designed for improving the precision and removing the data from blind area.[Chinese Medical Equipment Journal，2015，36（8）：1-5，9]

accelerometer;angle detection;optimal control algorithm;error analysis

R318；R683；TP391.4

A

1003-8868（2015）08-0001-06

10.7687/J.ISSN1003-8868.2015.08.001

天津市科技支撑计划重点项目（14ZCZDSY00009）

秦晓丽（1986—），女，研究实习员，主要从事控制理论与控制工程方面的研究工作，E-mail：qinxl_0704@126.com。

300161天津，军事医学科学院卫生装备研究所（秦晓丽，谢新武，杨 健，孙秋明，倪爱娟，田 丰）；100084北京，清华大学医学院（谢新武）

田 丰，E-mail：tianfeng62037@163.com