分形原理评估特殊曲线测量精度：以海岸线为例

引文格式： 廖永生. 分形原理评估特殊曲线测量精度[J].测绘通报，2015(4)：65-68.DOI:10.13474/j.cnki.11-2246.2015.0112

分形原理评估特殊曲线测量精度——以海岸线为例

廖永生

(广西壮族自治区地理国情监测院，广西 南宁 530023)

TheFractalTheoryinAnalyzingSpecialCurveMeasurementAccuracy

——TakingCoastlineSurveyingasanExample

LIAOYongsheng

摘要：特长曲线的高精度测量处理一直是地理信息数据处理的难题。海岸线作为空间数据中的最长动态曲线之一，其数据精度依赖于海岸线测量点的采样和分形。本文海岸线测量采用了高精度测量方法；同时基于海岸线分形原理，可以采用增加采样点的方法来提高海岸线的测量精度；最终采用Beizer曲线方法对数据进行加工，生成最佳高精度海岸线。

关键词：海岸线测量；分形；Beizer曲线；维数

中图分类号：P229

收稿日期：2014-01-07

基金项目：国家海洋公益项目(201305023)

作者简介：廖永生(1979—)，男，硕士，高级工程师，主要从事3S技术集成和地球空间信息数据应用的研究。E-mail：188249620@qq.com

一、引言

在对空间实体特别是大型空间实体测量绘制中，存在大量非直线的线状，即空间曲线。空间曲线包括规则曲线和不规则曲线。实际测量中，规则曲线(圆、椭圆)可以采用测量多个点的坐标后建立曲线数学模型的方法绘制矢量曲线；不规则曲线一般采用测量多个点的方法来绘制曲线，如等高线的测绘。

实际测绘中，对小型实体曲线的绘制可以采用测量较多点的方法，获得的结果和真实值差异不大。但是对于一些大型曲线的绘制，由于不可能实现曲线点的密集采样，测量时需根据实际情况进行采样，由于测量方法和要求不同，测量采样点的密度和精度也不同。

在对道路、海岸线、河道，以及边境进行测量时，由于曲线不规则且长度值较大，采样点的密集程度将会直接影响曲线的精度。特别是海岸线的测量，由于海岸线位置测量和长度测量对海洋研究和海岸带保护具有相当重要的意义，因此在海岸线测量时，必须尽可能获得海洋线高精度数据，包括位置数据和长度数据。

广西大陆海岸线测量是国家908专项广西海洋资源调查中海岸带调查的重要组成部分，其目标是掌握广西海岸线的准确空间位置、长度和岸线类型。在测量和数据处理中，本文采用分形法实现对海岸线的采样点加密和精度评估，最终获得了较高精度的广西大陆海岸线数据。

二、海岸线测量基本步骤

由于海岸线的动态变化，其界定比较困难，包括采用零米线界定、平均潮位线确定等方法。海岸线测量采用网络RTK测量的方法，即一般采用平均痕迹线的界定方法。由于海岸线是非规则曲线，一般需要尽可能测量曲线的拐点，但是由于测量员自身无法真正掌握其所在海岸线曲线的情况，需要按照两个原则进行采样：在一般地区平均每50m采样一次，在前后目视状况比较复杂的地方平均每30m采样一次，在前后目视极端的地方每10m采样一次；每次采样均记录岸线性质和影像等数据。

网络RTK测量即流动站连接广西CORS系统进行测量，其测量平面精度可达到5cm以内。

测量完成后，直接通过采样点连线获得广西海岸线数据，但是由于采样点间隔过长，其位置精度较差，因此需要对海岸线点进行加密，才能保证海岸线长度和空间位置的精度。在广西大陆海岸线测量中，采用了海岸线分形原理和数学模型实现了岸线采样点的加密。

三、海岸线分形原理和模型

1. 海岸线分形基本理论

海岸线是分形领域最传统的课题，美国科学家Mandelbrot于1967年在《科学》上发表的题为《英国海岸线有多长？》一文中就阐述了海岸线长度不确定性的问题，并由此提出了分形与分维的概念，成为分形理论的起源。

通俗地说，海岸线分形原理就是海岸线采样点的密度差异，密度越高，其岸线长度和空间位置越准确。理论上，海岸线精度只能逼近真实值而永远无法达到真实值。

广西大陆海岸线测量中，根据成图比例尺，采样点的间隔，以及海岸线测量精度与海岸线长度也不同，如图1所示。

图1　不同比例尺下的海岸线采样和分形

根据分形理论的基本观点，由于量测标度不同，海岸线的长度不是一个确定值。随着量测标度趋向精细，海岸线的实际长度也随之增大。

即使是精确测量获得的海岸线，其长度不确定性的问题仍然存在。因此，在部门决策或是执行的过程中就有可能产生下述问题，即在同样的区域范围内对某段海岸线进行的量测，由于使用的量测标度不同，或是虽然使用了同样的标度，但是基于不同比例尺的地图，就会产生一系列的数据误差，为决策的制定与顺利施行带来不利的影响。

因此，需要根据海岸线的复杂程度，增加其采样点，提高海岸线测量数据的精度。

2. 广西大陆海岸线复杂度计算

目前计算分形维数的主要方法包括网格法、脚规法(量规法)、盒子法、折线法、方差图法、函数叠加熵计算方法等。广西大陆海岸线测量数据处理采用了量规法计算分形维值，并通过折线法检验其计算准确性。

分形理论基本公式如下

式中，rn为特征线度；Nn为物体数目；C为比例常数；D为分形维数。由上式推导可得

式中，Nn与岸线长度Ln成正比关系，即Ln=Nnr。

海岸线中每段都有不同的分形维数，总的分形维数计算公式为

在每段海岸线维数的计算中，不可能计算每段的海岸线的分形维数，因此可以采用统计的方法绘制每段计算值的散点分布图，并采用最小二乘法的方法计算出最佳维数值。

广西大陆海岸线测量成果共有31469个测量点，总长1628.59km，平均每52m一个采样点。根据该数据，对海岸线进行分形维数计算，获得的结果见表1。

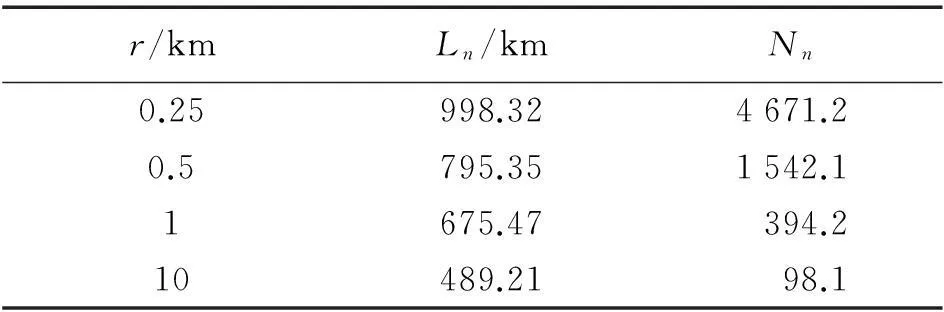
表1　广西海岸线不同段的分形部分计算统计表

根据对数分布统计，建立Ln—r的对数关系，则

lnL(r)=-1.819lnr+2.343

广西大陆海岸线维数最终计算结果为D=2.784。该数值为广西大陆海岸线测量获得的复杂程度描述。该数值远大于其他资料中海岸线分形维数的数值，原因是海岸线为实际测量，其精度远高于其他资料中通过卫星影像获得的海岸线数据计算的分形维数。

对海岸线实现采样点的自动加密，可以进一步提高海岸线的分形维数，从而提高海岸线测量数据的精度。

四、海岸线分形插值方法

分析广西海岸线复杂程度，可以针对不同地段的复杂程度进行内插值，增加采样点数量，并采用分形插值的方法实现采样点加密。

由于海岸线的绘制是采用直线连线的方法，因此在增加采样点时，可采用趋势值曲线变化内插采样点的方法实现，即按照采样点的顺序，间隔一个点或两个点预测曲线的走向趋势，从而增加相关采样点。

根据曲线原理，走向趋势可以根据其线性求导实现，在参数曲线中，可以采用如下方程表示矢量曲线

p(t)=(x,y)=(x(t),y(t))t∈[a,b]

式中，(x,y)为采样点坐标。如果采样点坐标遵循一点的线性方程函数，则坐标为(x(t),y(t))。由于海岸线的采样点无线性函数关系，因此，可以通过其直线趋势，改变曲线方程，增加采样点,曲线化后如图2所示。

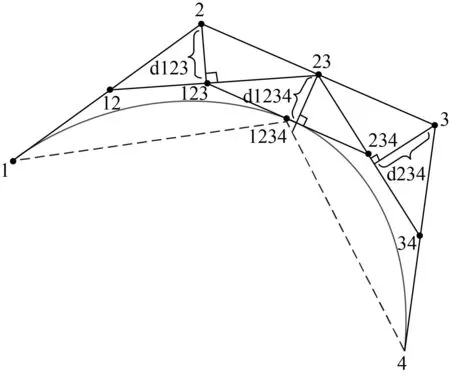
图2　多次插值后的新曲线

根据曲线的导线公式[7]，如果曲线是导曲线，即曲线P=P(t)在t=t0处n阶参数连续，如果它在t0处n阶左右导数存在，并且满足

根据Bernstein的曲线基函数公式

原有线性方程根据采样点的数量，可以转成曲线方程，如下

其导数方程为

其中

经过推导，可得

则根据n的数值，可以推导获得不同阶的曲线，即Beizer曲线。Beizer曲线根据其推演阶数，可以分为一阶、二阶、三阶，以及三阶以上的曲线。各阶Beizer趋向方程如下：

一阶Beizer曲线方程为

(1-t)P0+tP1

二阶Beizer曲线方程为

三阶Beizer曲线方程为

P(t)=B0,3(t)P0+B1,3(t)P1+B2,3(t)P2+B3,3(t)P3

式中

一般情况下，海岸线加密采样点采用二阶和三阶Beizer曲线，获得大量的曲线加密点，特别是高加密点，从而提高海岸线的分形维数。图3和图4是采用Beizer曲线加密前后的对比。

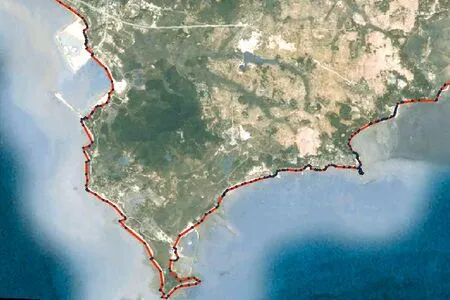
图3　实际测量点连线

图4　Beizer插值后的光滑曲线

对500km的海岸线采用Beizer曲线化，其分形维数已经超出了一般计算值(最高超过3)，显然超出了一般计算数据，但也说明了实际曲线的精度情况。由于自然岸线以曲线为主，只有在人工岸线的地带(海堤、港口)，岸线比较规整，因此，在自然岸线中，可以采用Beizer算法绘制Beizer曲线，使海岸线的绘制更加高精度化和自然化。

五、结束语

本文通过海岸线分形理论，计算出海岸线的分形维数，在总体上显示海岸线的复杂程度，但也可以显示海岸线采样点的疏密程度。通过分形维数计算后，根据其分形维数大小，采用一定的方法进行采样点插值，可以增加采样点数量，提高采样点的密集程度，提高海岸线精度。Beizer曲线是精度比较高的插值算法，在数据处理中，可以采用二阶或三阶Beizer曲线。

Beizer曲线插值使海岸线测量精度大幅度提高，也使海岸线分形维数有一定程度提高。采样点越多，则海岸线分形维数越高。对海岸线的分形维数进行计算和插值，实现大型曲线的高精度数据，还可用于公路、境界和河流等地理实体的测量数据处理，对于地理信息数据采集有着重要的借鉴意义。

参考文献：

[1]马小峰，赵冬至，邢小罡，等.海岸线卫星遥感提取方法研究[J]．海洋环境科学，2007，26(2)：185-189.

[2]朱晓华，蔡运龙.中国海岸线分维及其性质研究[J].海洋科学进展，2004，22(2)：156-162.

[3]周江，印萍，程荡敌，等.基于GIS和分形理论研究的海岸线图像和分维以及长度[J].海洋地质与第四纪地质，2008,28(4)：65-71.

[4]黄小葳.分形维数计算程序的设计及其应用[J].北京联合大学学报：自然科学版，2004,18(4)：33-36.

[5]叶小敏，纪育强，郑全安，等.胶州湾海岸线历史变迁的分形分析[J].海洋科学进展，2009,27(4)：495-501.

[6]朱晓华，王建.海岸线空间分形性质探讨——以江苏省为例[J].地理科学，2001，21(1)：70-75.

[7]徐甜，刘凌霞.Bezier曲线的算法描述及其程序实现[J].安阳师范学院学报，2006(5)：49-52.

[8]邓重阳，汪国昭.曲线插值的一种保凸细分方法[J].计算机辅助设计与图形学学报，2009(8)：1042-1046.

[9]高义，苏奋振，周成虎，等.基于分形的中国大陆海岸线尺度效应研究[J].地理学报，2011，66(3)：331-339.

[10]张国华，黄韦艮.基于分形的海岸线遥感信息空间尺度研究[J].遥感学报，2006，10(4)：463-468.

[11]陈霞，王建.用分形方法研究海岸线的长度[J].海洋科学，2002，26(12)：32-35.