多重网格技术在侧喷干扰流场模拟中的应用*
2015-12-26薄靖龙刘耀峰
薄靖龙,刘耀峰,曹 宁
(中国航天空气动力技术研究院,北京 100074)
多重网格技术在侧喷干扰流场模拟中的应用*
薄靖龙,刘耀峰,曹宁
(中国航天空气动力技术研究院,北京100074)
摘要:开展了多重网格技术在侧向喷流干扰流场数值模拟中的应用研究。采用修正的限制算子和回插算子,解决了多重网格技术在超声速/高超声速侧向喷流干扰流场模拟中的稳定性问题。使用全近似(FAS)格式和两重网格V循环,数值模拟了不同条件下的单、多喷流干扰流场,计算结果表明:应用修正算子的多重网格技术可以显著提高侧向喷流干扰流场计算的收敛速度,并且计算稳定性好。
关键词:多重网格技术;高超声速;侧向喷流;喷流干扰;数值模拟
0引言
随着航空航天飞行器向着更高空、更高速、更高效的方向发展,在越来越多的飞行器上采用侧向喷流控制技术进行姿态或轨道控制。侧向喷流进入高速主流引起的复杂干扰流动,构成了最复杂的流场之一,在这种流场中包含着激波/边界层干扰、激波/激波干扰、流动分离与再附、漩涡等一系列复杂流动现象[1-5],图1给出了典型模型对称面上的复杂侧向喷流干扰流场结构示意[5]。
由于侧喷干扰流场结构复杂,特别是位于喷口附近的流场,物理参数变化异常剧烈,为准确预测流场中存在的复杂流动现象,需要根据流动特点进行针对性的网格加密,从而导致网格量较大,在工程应用中对于部分外形复杂的飞行器(如包含多喷流、多舵面等),网格量过大这一特点尤其显著。加之工程应用中计算状态多,往往多达上万组,在现有计算方法与计算资源条件下,难以满足工程计算任务的需要。因此,采取合适的加速收敛措施,提高侧喷干扰流场的收敛速度具有重要的工程应用价值。
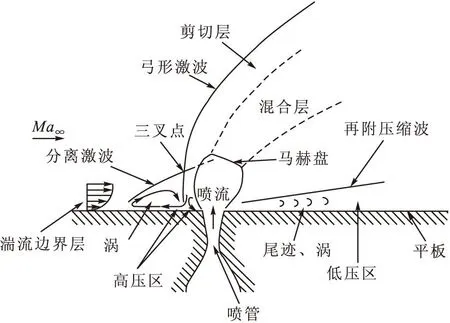
图1 侧向喷流干扰流场结构示意图
在诸多的加速收敛技术中,多重网格法是非常有效的方法之一。多重网格技术的核心思想是迭代误差可以分为高频摆动分量和低频光滑分量,先在细网格上消除高频误差,而在细网格上不易消除的低频误差,用粗网格修正消除,这样通过一系列变粗的网格就可以很快消除各种频率的误差,达到加速收敛的目的。传统多重网格技术在亚跨声速流场中得到了广泛的应用,牟斌等利用多重网格技术模拟了NLR7301 case#1两段翼低速绕流以及DLRF4跨声速流场[6],效果显著。杨爱明等利用多重网格方法显著的加快了跨声速旋翼流场的收敛[7],唐智礼等细致处理了多重网格方法的细节,计算了跨声速三角翼流场及跨声速翼身组合体外形,结果表明多重网格方法显著提高了计算效率。在超/高超声速流场数值模拟应用中,其计算稳定性比较差,其中最主要的问题是在限制和回插过程中导致在驻点及激波前后区域产生负压力及负密度。为提高其在超/高超声速流场模拟中的鲁棒性与稳定性,Radespiel等人[9]通过修正限制算子来限制强激波区域扰动向上游传播,Zhu等人[10]通过修正回插算子来限制负压力等非物理现象的产生,均取得了一定的效果。
文中尝试将多重网格技术应用于超声速高超声速来流与超声速喷流相互干扰流场的数值模拟,以提高计算效率,减少计算成本。文中多重网格技术应用全近似(FAS)格式,采用两重网格V循环,使用修正后的限制算子和回插算子,计算了不同条件下的侧向喷流干扰流场,通过与单重网格计算结果和收敛历程的对比,表明多重网格技术不会影响最终的收敛结果,并且加速收敛效果明显。
1数值模拟方法
1.1 控制方程和离散方法
采用三维可压缩Navier-Stokes方程为控制方程,通过有限体积方法进行离散,对流项离散采用Roe格式[11],通过MUSCL插值达到二阶精度,粘性项离散采用中心差分格式,时间项离散使用隐式LU-SGS方法[12]。湍流模型采用S-A一方程模型[13]。
1.2 多重网格技术
文中多重网格技术采用FAS格式,两层网格V循环。具体计算步骤如下:在细网格上迭代数步之后,将结果与残值通过体积加权平均限制算子传递到粗网格上,在粗网格经过一定步数迭代之后将结果通过回插算子传回到细网格,如此循环,直到结果收敛。
对于高超声速流动而言,限制算子和回插算子对于计算结果的收敛性和稳定性起到了主要的作用。以下详细介绍这两个算子:
限制过程由式(1)给出:
(1)
回插过程由式(2)给出:
(2)
为保证强激波区域计算的收敛性,对于限制算子采用以下函数进行修正:
(3)
式中ε是与流动相适应的调节系数,可以根据流场中的压力梯度进行自适应调节。
(4)
式中的衰减系数k根据计算情况不同,一般取值0.5~1.0之间。νi、νj、νk为取决于流场压力梯度的参数,取值如下:
(5)
为避免回插过程中出现负压力和负密度,对于回插算子采用以下方式进行修正[14]:
(6)
式中:pA代表细网格上的原始值,pB代表将粗网格上的结果直接回插得到的细网格上的值。
2验证算例一:锥-柱-裙外形轨控喷流干扰流场
2.1 计算模型和计算条件
计算模型为图2所示的旋成体外形[15],模型由拱形头部、锥段、柱段和裙尾组成,喷口位于质心位置。计算采用分区对接结构网格,整体网格为“C-H”型,喷口附近网格为“O”型,考虑流场对称性,仅模拟全流场的一半区域,网格量约为600万,图3给出了喷口附近的网格布局。

图2 几何模型
计算条件由表1和表2给出,其中表1为来流条件,表2为喷流条件。根据文献描述,来流为层流流动。
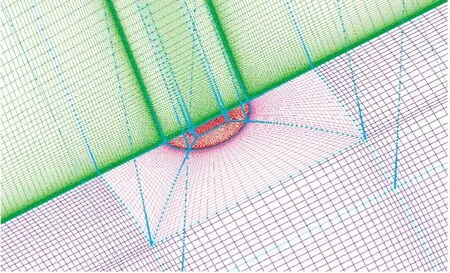
图3 喷口附近网格布局

来流马赫数Ma∞攻角α/(°)来流压力P∞/Pa来流温度T∞/K雷诺数Re8.00149.101264.1643.07×105

表2 喷流条件
2.2 结果与讨论
图4给出了表面及对称面等压力云图,从图中可以清楚的看到激波/激波干扰、激波/边界层干扰等流场特征。清晰的激波等流场结构表明修正后的多重网格技术可以模拟高超声速流场中存在的高压力梯度与速度梯度,并且从计算过程来看,计算稳定性较好。
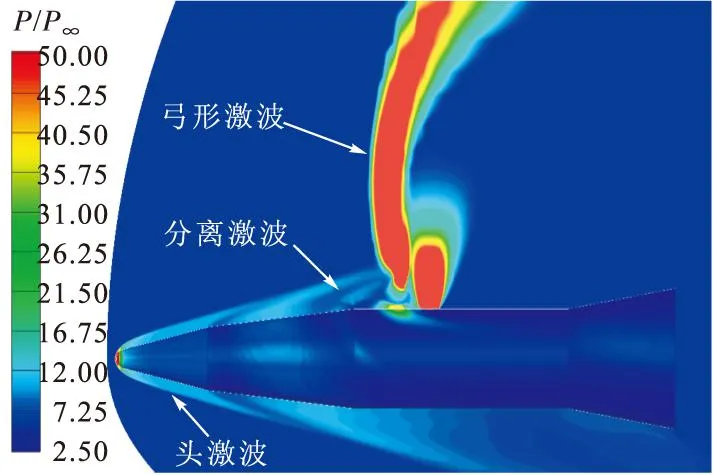
图4 表面与对称面等压力云图(Ma∞=8.0)
图5给出了喷口附近表面极限流线图,其中上半部分为采用多重网格技术所获得的计算结果,下半部分为单重网格方法计算结果,从图中可以看出两种方法计算得到的分离区大小几乎一样,分离和再附的位置比较一致。图6给出了喷口中心子午线上压力分布的比较结果,可以看出多重网格技术的计算结果和单重网格十分一致,误差在1‰以内。由此可见多重网格技术并不会改变流场的收敛结果,并且对于传统多重网格技术的修正是合理的,计算结果是正确的。
图7给出了有喷流干扰时的法向力收敛历程,图8给出了有喷流干扰时俯仰力矩的收敛历程,可以看出多重网格与单重网格得到的收敛结果一致,从而再次印证了多重网格技术不会改变喷流干扰流场的最终收敛结果。并且可以看出单重网格获得收敛结果大约需要32 000步,而多重网格只需要7 000步,考虑到多重网格单步计算时间约为单重网格单步时间的1.4倍,实际收敛加速比在3以上,说明了文中采用的多重网格技术具有良好的加速收敛效果。

图5 喷口附近表面极限流线比较图
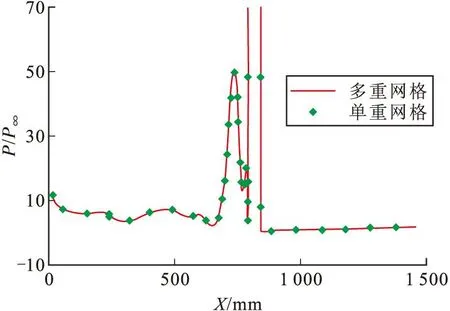
图6 喷口中心子午线压力分布
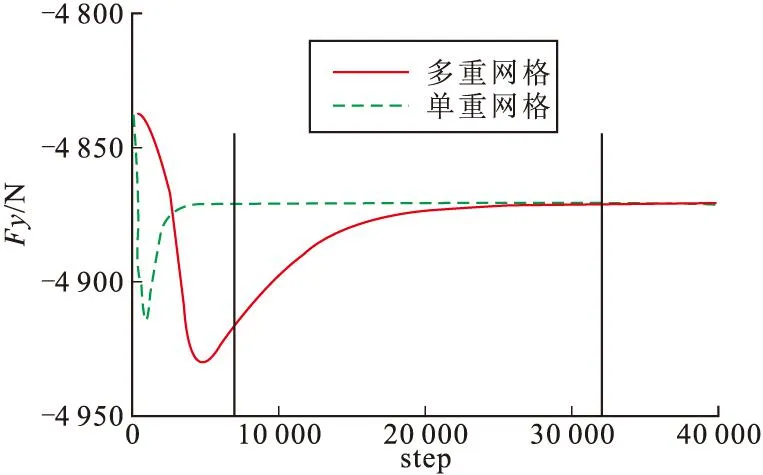
图7 法向力收敛历程(有喷流干扰)
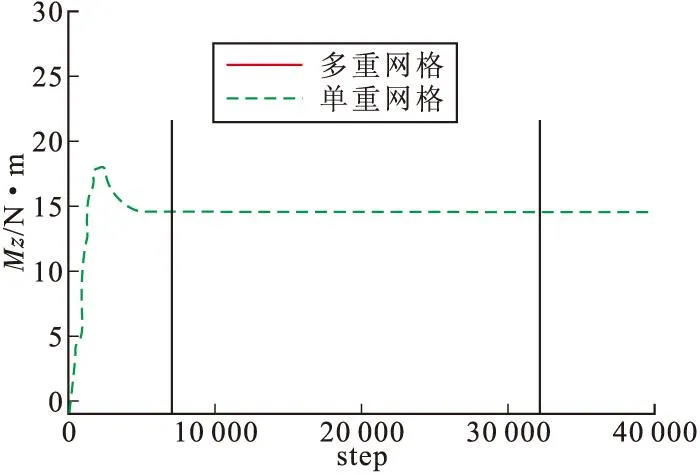
图8 俯仰力矩收敛历程(有喷流干扰)
3验证算例二:尖拱-柱外形多喷流干扰流场
3.1 计算模型和计算条件
计算模型为尖拱-柱形式的旋成体多喷流实验模型[16],如图9所示,在上表面对称线上纵向排列3个喷管。同样由于流场的对称性,仅模拟全流场的一半区域。喷管内的流场同外流场进行一体化计算。计算采用分区对接结构网格,半模网格量约为375万,图10给出了喷口附近网格布局。
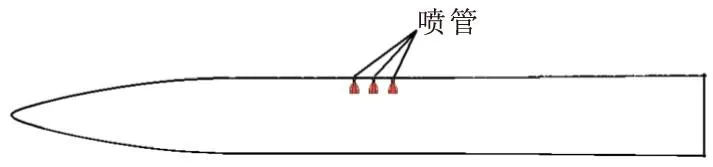
图9 几何模型及喷管位置
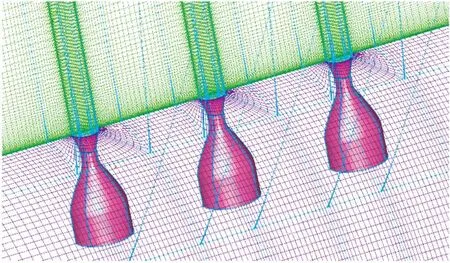
图10 喷口附近网格布局
自由来流、喷流都以空气作为介质。计算参数按照风洞实验条件给定,见表3。依据实验条件,来流为湍流状态。

表3 计算条件
3.2 结果与讨论
图11给出了利用多重网格方法计算得到的表面及对称面等压力云图,从图中可以清楚地看到激波/激波干扰、激波/边界层干扰等流场特征。图12给出了喷口附近的表面极限流线图,其中上半部分为多重网格计算结果,下半部分为单重网格计算结果,可以看出表面流谱一致,分离与再附的位置相同。
图13与图14分别给出了喷口中心子午线上压力分布与实验结果以及与单重网格结果的比较,可以看出计算与实验符合较好,同时多重网格与单重网格的计算结果吻合较好,表明了多重网格方法在复杂多喷流干扰流场模拟中的有效性与正确性。
图15给出了法向力系数的收敛历程,可以看出利用多重网格方法,大约6 000步即可得到收敛解,而单重网格方法约需要42 000步才能获得收敛结果。综合比较单重网格与多重网格的收敛计算时间,实际收敛加速比在5左右,体现了良好的加速收敛效果。

图11 表面与对称面等压力云图(Ma∞=4.9)
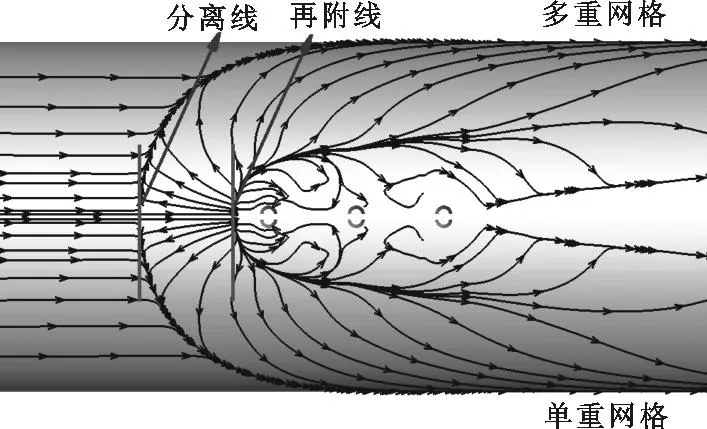
图12 喷口附近表面极限流线比较图
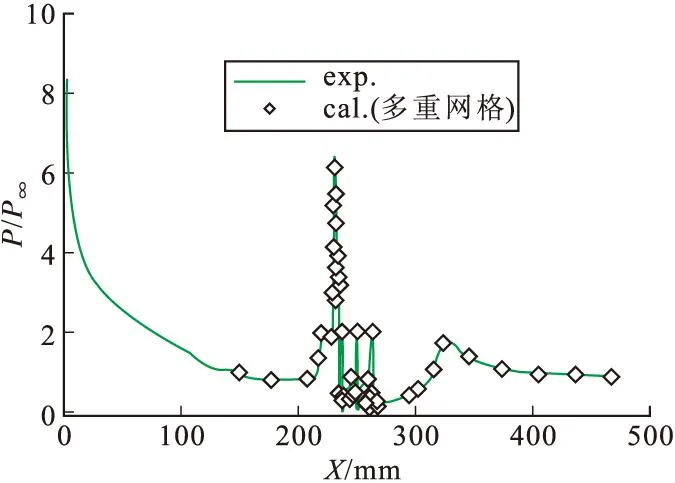
图13 喷口中心子午线压力分布实验计算对比
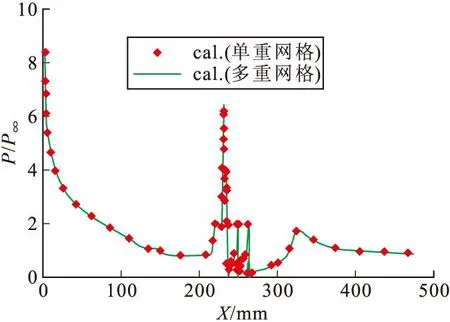
图14 喷口中心子午线压力分布两种计算方法结果对比
通过对尖拱-柱外形多喷口布局算例的结果分析,进一步说明了文中采用多重网格技术能够显著提高喷流干扰流场的收敛速度,并且结果是准确可信的。
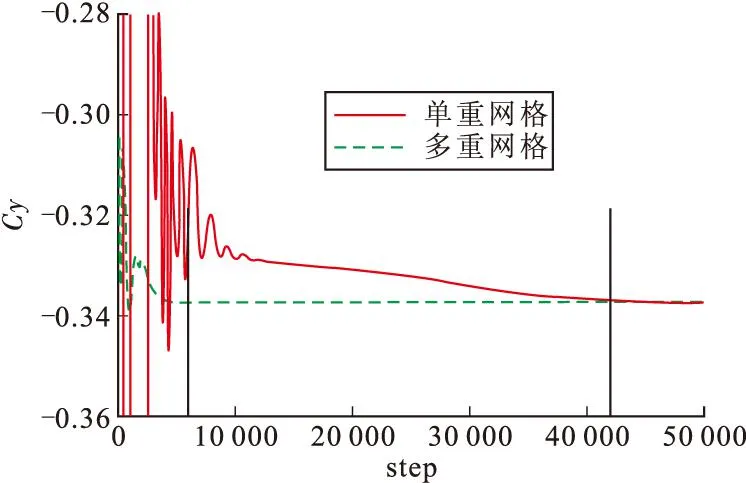
图15 法向力系数收敛历程(有喷流干扰)
4结论
文中利用多重网格技术数值模拟了两种外形条件下的侧向喷流干扰流场。通过文中的研究,可以得到以下结论:
1)采用修正的限制算子和回插算子,成功的将多重网格技术应用于非常复杂的超声速/高超声速侧向喷流干扰流场的数值模拟,计算稳定性好,并且不会影响最终的收敛结果;
2)多重网格技术在侧向喷流干扰流场模拟中具有好的加速收敛效果,可显著提高计算效率,对于复杂侧向喷流干扰流场计算具有较高的工程应用价值。
参考文献:
[1]Aso S, okuyama S. Experimental Study on Mixing Phenomena in Supersonic Flows with Slot Injection, AIAA 1991-0016 [R]. 1991.
[2]Gruber M R, Nejad A S, Dutton J C. Circular and elliptical transverse injection into a supersonic crossflow-the role of large-scale structure, AIAA 1995-2150 [R]. 1995.
[3]J G Santiago, J C Dutton. Crossflow vortices of a jet injected into a supersonic crossflow [J]. AIAA Journal, 1997, 35(5): 915-917.
[4]李素循. 近空间飞行器的气动复合控制原理及研究进展 [J]. 力学进展, 2009, 39(6): 740-755.
[5]倪招勇. 横向喷流诱导的复杂流场结构研究 [D]. 北京: 中国航天空气动力技术研究院, 2005.
[6]牟斌, 肖中云. 多重网格技术在复杂粘性流场中的应用及研究 [J]. 空气动力学学报, 2006, 24(1): 51-54.
[7]杨爱明, 翁培奋. 用多重网格技术计算旋翼跨声速无粘流场 [J]. 空气动力学学报, 2004, 22(3): 313-318
[8]唐智礼. 用隐式多重网格法计算三维粘性流动 [J]. 航空学报, 1998, 19(3): 327-331.
[9]Radespiel R, R C Swanson. Progress with multigrid schemes for hypersonic flow problems [J]. NASA CR 189579, 1991., okuyama S. Experimental Study on Mixing Phenomena in Supersonic Flows with Slot Injection, AIAA 1991-0016 [R]. 1991.
[2]Gruber M R, Nejad A S, Dutton J C. Circular and elliptical transverse injection into a supersonic crossflow-the role of large-scale structure, AIAA 1995-2150 [R]. 1995.
[3]J G Santiago, J C Dutton. Crossflow vortices of a jet injected into a supersonic crossflow [J]. AIAA Journal, 1997, 35(5): 915-917.
[4]李素循. 近空间飞行器的气动复合控制原理及研究进展 [J]. 力学进展, 2009, 39(6): 740-755.
[5]倪招勇. 横向喷流诱导的复杂流场结构研究 [D]. 北京: 中国航天空气动力技术研究院, 2005.
[6]牟斌, 肖中云. 多重网格技术在复杂粘性流场中的应用及研究 [J]. 空气动力学学报, 2006, 24(1): 51-54.
[7]杨爱明, 翁培奋. 用多重网格技术计算旋翼跨声速无粘流场 [J]. 空气动力学学报, 2004, 22(3): 313-318
[8]唐智礼. 用隐式多重网格法计算三维粘性流动 [J]. 航空学报, 1998, 19(3): 327-331.
[9]Radespiel R, R C Swanson. Progress with multigrid schemes for hypersonic flow problems [J]. NASA CR 189579, 1991.
[10]Zhu Z W, P Alavilli, C Lacor. Efficiency and robustness of multigrid methods for hypersonic flows, AIAA 1997-0342 [R]. 1997.
[11]Roe P L. Approximate riemann solvers, parameter vectors and different schemes [J]. Journal of Computational Physics, 1981, 43: 357-372.
[12]Yoon S, A Jameson. Lower-upper symmetric-gauss-sediel method for the euler and navier-stokers equations [J]. AIAA Journal, 1988, 26(9): 1025-1026.
[13]P R Spalart, S R Allmaras. A one-equation turbulence model for aerodynamic flows, AIAA 1992-0439 [R]. 1992.
[14]Kim S S, C Kim, O H Rho. Multigrid algorithm for computing hypersonic, chemically reacting flows [J]. Journal of Spacecraft and Rockets, 2001, 38(6): 865-874.
[15]S M Dash, E R Perrell. Lateral jet aerodunamic interaction simulations for dynamic pressure loads, AIAA 2000-2036 [R]. 2000.
[16]刘耀峰, 李素循, 倪招勇. 多喷口布局对气动特性影响: 大型客机计算流体力学应用与发展 [M]. 上海: 上海交通大学出版社, 2009: 295-302.
收稿日期:2014-07-06
作者简介:薄靖龙(1988-),男,河南内乡人,助理工程师,硕士,研究方向:流动数值模拟。
中图分类号:V211.3
文献标志码:A
Application of Multigrid Method in Lateral Jet Interaction
Flowfield Simulation
BO Jinglong,LIU Yaofeng,CAO Ning
(China Academy of Aerospace Aerodynamics, Beijing 100074, China)
Abstract:The investigation of multigrid method for supersonic/hypersonic lateral jet interaction flowfield simulation is conducted. To overcome the instability problem in applying the multigrid method to supersonic/hypersonic lateral jet interaction flows, some modifications are carried out to the restriction and prolongation operators. The modified multigrid method using FAS strategy (2-level, V-cycle) is applied to computation of lateral jet interaction flowfield for different conditions. The results reveal the robustness of the modified multigrid scheme and substantial speed-up in hypersonic lateral jet interaction flowfields simulation.
Keywords:multigrid method; hypersonic; lateral jet; jet interaction; numerical simulation
