空地反辐射导弹激光近炸引信目标识别方法*

诸德放,张　真,王文强

(1　空军勤务学院, 江苏徐州　221000;2　93033部队, 沈阳　110000;3　93069部队, 辽宁普兰店　116200)

空地反辐射导弹激光近炸引信目标识别方法*

诸德放1,张真2,王文强3

(1空军勤务学院, 江苏徐州221000;293033部队, 沈阳110000;393069部队, 辽宁普兰店116200)

摘要:为实现激光引信对雷达目标的探测识别,提出了基于多路窄波束激光测距的目标识别方法,建立了以测距值的突变来识别目标高度和宽度的数学模型;在光路数目一定时,通过求解探测平面内目标出现概率密度函数的Lebesgue积分,确定了使探测概率最大的最优光路间夹角,并对典型的弹目交会情形进行了仿真分析。结果表明,探测概率随导弹进入角的减小、目标天线高度的增加而增大,最优光路夹角呈中间密、两边疏的排列。

关键词:反辐射导弹;激光近炸引信;目标识别;探测概率;误差分析;光路优化

0引言

为提高弹药的毁伤效果,现代弹药中大量配用近炸引信。激光引信因探测距离远、测距精度高以及抗电磁干扰能力强而得到广泛应用[1-3]。对空地导弹而言,使用时需从复杂的地物、地貌背景中将目标探测、识别出来,才能确保适时起爆战斗部实现最佳的引战配合达到预期的毁伤效果[4]。文中以空地反辐射导弹脉冲测距体制激光近炸引信为应用背景,分析典型目标的几何外形识别方法、探测概率及光路优化。

1弹目交会特点分析

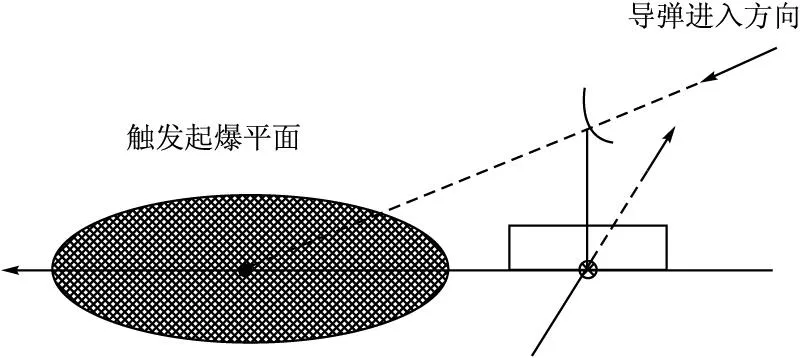
图1　触发起爆炸点散布示意图

ARM在攻击过程中以目标雷达的馈源点(即雷达天线的几何中心)为瞄准点,其末端弹道近似为一条与地面成一定角度的直线,如图1所示。因为雷达馈源点离地面有一定高度,导弹在地面的散布中心与天线馈源点在地面的垂直投影不重合,所以可以确定导弹末弹道与地面的交点大部分会落在目标后方[5-6]。当采用触发引信进行起爆时,导弹落点散布的等概率椭圆中心位于目标后方,导弹的大部分炸点落在离目标较远的后方,这使得导弹触发起爆的毁伤效果大大降低,尤其在弹道倾角较小、雷达馈源点较高时, 情况更为严重。

针对这种特殊的弹目交会情

况,国外先进的空地反辐射导弹多配有“触发+激光近炸”的复合引信[7]。此类引信只有在有效识别目标的前提下,才能适时起爆战斗部实现对目标的最佳毁伤。文中主要对反辐射导弹激光近炸引信对典型目标的外形识别、探测概率等方面进行研究。

2目标几何外形的识别

2.1　基本假设

为了便于分析,现作如下假设和简化:

①激光引信采用多路发射、多路接收,各发射、接收装置的工作相互独立;

②发射的激光为窄波束,发散角足够小,在有效作用距离内光束可以看作一条直线;

③各发射激光束在同一平面内;

④弹体在滚动方向稳定,滚转角为零;

⑤在以目标为中心的一定区域内,地面背景为平面。

2.2　数学模型的建立

如图2所示,设A为激光引信的安装点,导弹弹轴延长线与地面的交点为W,AW与地面的夹角ω即为导弹的俯仰角。探测面具有前倾角θ以确保在高速弹目交会条件下,留有足够的时间进行目标识别并在最佳位置引爆战斗部。弹体纵向对称面与探测平面的交线为AM,光束AB、AC、AD、AE与AM的夹角为α1、α2、α3、α4,并规定从弹尾向弹头看各光路与AM所形成的夹角,逆时针为正、顺时针为负。

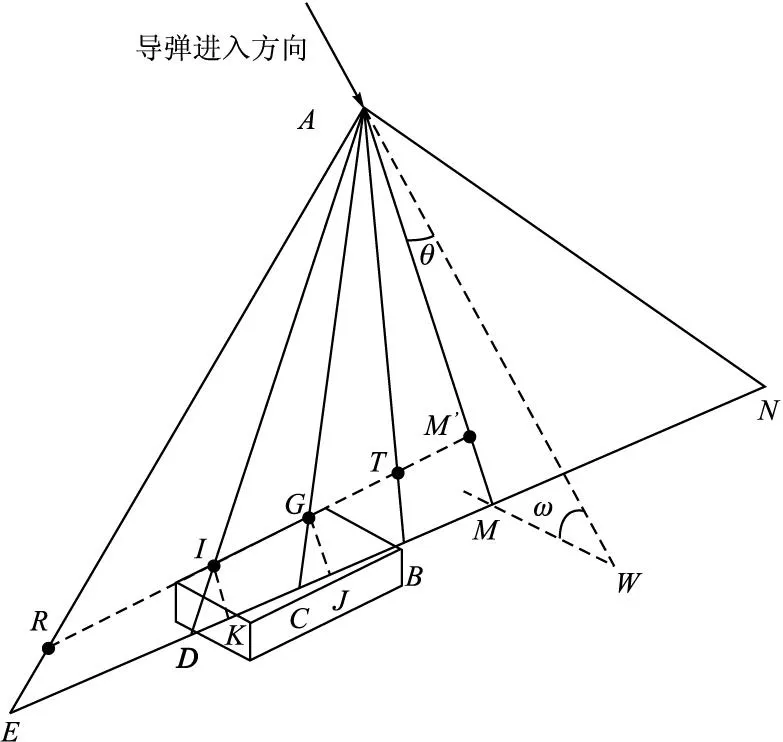
图2　激光近炸引信探测目标示意图

2.3　高度识别

由几何关系可知,探测平面AEN与地面的夹角为θ+ω。对于高度为h1的目标而言,光束AD在扫到目标前后测量距离发生的突变为DI=x1。

(1)

h1=x1sin(θ+ω)cosα3

(2)

由于激光测距、弹上姿态角传感器均存在测量误差,故计算得到的h1对应一个高度范围[h1min,h1max]。

同理,对于光束AC在扫到目标前后,测量距离发生的突变为CG=x2。该突变对应目标高度的计算值为h2=x2sin(θ+ω)cosα2,目标的实际高度范围为[h2min,h2max]。

2.4　宽度识别

由于导弹具有一定的制导精度,在激光引信的作用范围内,两路光束同时扫过目标的概率很大。因此,若在探测平面内AD、AC的测距值均发生突变,且通过突变值计算所得到的目标实际高度范围有交集,即[h1min,h1max]∩[h2min,h2max]≠∅,则可认为两路光束扫过同一物体。

当光束扫到目标时,其测距值发生突变,而没有扫到目标的光路不会发生测距突变。根据光路间的夹角的位置关系和测距值可以估计出目标在探测平面内的宽度范围。以光路AC、AD扫到目标为例,目标在探测平面内宽度的最小值Wmin应为线段GI的长度,即:

(3)

目标在探测平面内宽度的最大值Wmax应为线段RT的长度,即:

由△AIG面积相等可知:

因此有:

(4)

由式(3)、式(4)可以确定目标在探测平面内的宽度范围:W∈[Wmin,Wmax)。

3探测概率及光路优化

空地反辐射导弹激光引信对目标的探测概率及在宽度上对目标的识别精度与光路数目及光路间夹角密切相关。如果在探测视场内光路总数足够多,相邻光路间的夹角趋于零,则可实现在探测视场内对目标宽度的精确识别。但在实际应用中,由于成本、体积、安装位置的限制,仅能实现有限光路的探测。因此对于光路总数有限时,必须优化光路间的夹角才能获得最大的目标探测概率。

3.1　目标在探测平面内的位置描述

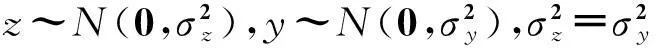
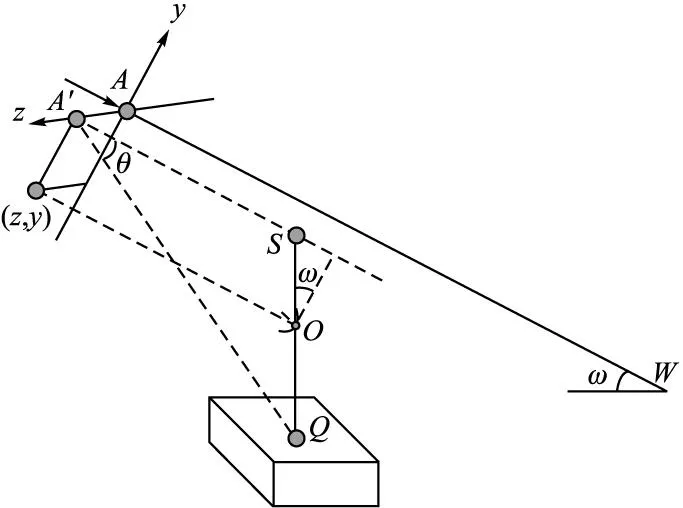
图3　弹目交会示意图

由几何关系可知:

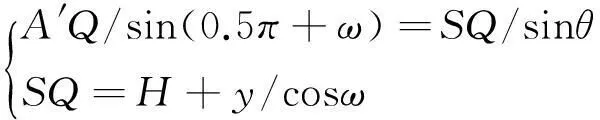
(5)

因此,A′Q=(Hcosω+y)/sinθ。在如图4所示的探测平面Az′y′内,目标宽度中心点的坐标为Q(z′,y′),其中z′=z,y′=(Hcosω+y)/sinθ。由正态分布的性质可知,Q(z′,y′)在探测平面内各点出现的概率密度为:

(6)

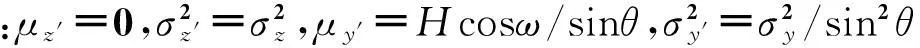
图4　目标可探测区域示意图

3.2　探测到目标的条件

设目标在引信探测面内的宽度为b,则其宽度方向的两端点坐标分别为Q1(z′+0.5b,y′),Q2(z′-0.5b,y′);A′Q1、A′Q2与A′M的夹角为β1、β2。引信的探测概率可以在探测平面A′z′y′内由Q(z′,y′)的概率密度函数在可以探测到的区域内进行积分求得。如图4所示,当Q(z′,y′)位于可探测区域时,至少有一路光束扫过线段Q1Q2,即存在i∈{1,2,…,n},使得β1≤αi≤β2成立。

3.3　最优光路夹角的确定

由于Lebesgue积分是按照集合划分积分区域的,故可以方便的求解该探测概率问题。当光路数n确定时,求解光路之间最优夹角使得探测概率P=∫Eg(z′,y′)dμ最大可以归纳为如下问题:

(7)

当光路数目n已定时,可以将光路夹角按照一定步长离散化,通过Monte-Carlo方法求解最优光路夹角的近似解。

4仿真结果及分析

4.1　最大探测概率的仿真分析

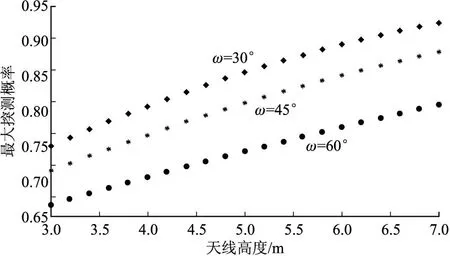
图5　探测概率与天线高度、俯仰角的关系

由图3可知,只有当A′Q=(Hcosω+y)/sinθ大于零,激光束才有可能扫到目标,否则导弹将落于目标前方或直接撞击目标。设导弹的制导误差CEP=5 m,导弹的俯仰角ω=30°,45°,60°,目标雷达天线高度h=3~7 m,对目标探测概率的最大值如图5所示。由图5可以看出,随着目标高度的增加、弹体俯仰角的减小,引信对目标探测概率的最大值不断增大。这是因为反辐射导弹以目标雷达天线为瞄准点,末端弹道近似为一条直线,导弹的进入角(近似等于弹体俯仰角,两者相差一个较小的攻角)越小、目标天线越高,导弹从目标上方掠过的概率越大,此时引信探测装置有可能探测到目标。导弹的进入角越大、目标天线越低,导弹在目标前方触地起爆或直接命中目标的概率越大。此类情况下激光引信无法探测到目标,但通常目标到炸点间距离很近在战斗部毁伤半径内,因此无需探测到目标实现近炸,仅靠触发起爆方式即可实现对目标的有效毁伤。

4.2　最优光路夹角确定的实例分析

设导弹的俯仰角ω=30°,探测平面的前倾角θ=30°,攻击的目标为“爱国者”系统相控阵雷达,其几何参数为长×宽×高=5.6 m×2.5 m×2.6 m,天线高度为5 m[9],仅考虑对雷达车体高度的探测识别。并定义漏警概率Pl:目标落在激光引信探测视场内,但没有探测到目标的概率,即Pl=1-P/P∞,其中P为探测概率,P∞为光路无限多时的探测概率。当光路夹角αi按照式(7)取最佳值时,探测器的各项性能指标如表1所示(由于光路的对称性,仅列出光路中αi≥0的部分)。

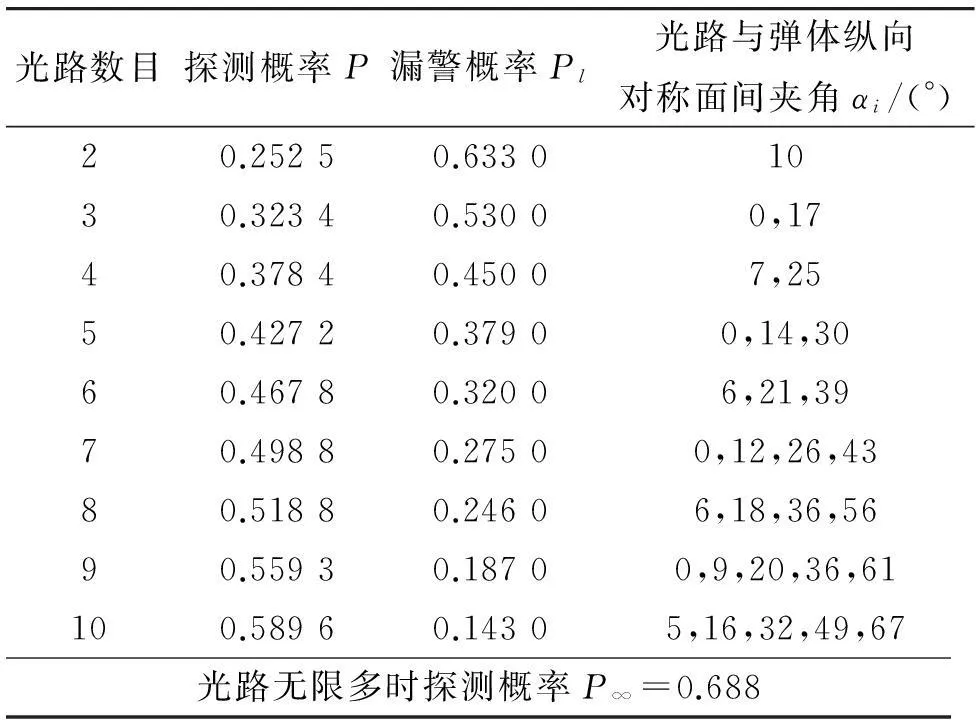
表1　光路数目一定时最优夹角安排及探测概率

从表中的计算结果可以看出,随着光路数目的增加,探测视场逐步增大,探测视场内光路间夹角逐渐减小,探测概率逐步增大,漏警概率减小。但随着光路数的增加,探测概率的增量递减,最终将逼近P∞。

5结束语

针对空地反辐射导弹激光近炸引信需从复杂地面背景中将目标探测、识别出来的实际需求,提出了一种基于多路窄波束激光测距的目标识别方法。该方法通过激光测距值出现突变计算目标高度,通过测距值及光路间夹角关系判断目标在探测平面内的宽度范围。在光路数目一定时,通过求解在探测平面内目标出现概率密度函数的Lebesgue积分,确定光路之间的最优夹角以实现探测概率最大。

通过对典型弹目交会情况仿真计算,结果表明:导弹的进入角越小,目标雷达天线越高,激光引信探测到目标概率的最大值越大;光路数目一定时,为了获得较大的探测概率,光路应以“外疏内密”的形式集中在弹体纵向对称面附近。

参考文献:

[1]张河. 探测与识别技术 [M]. 北京: 北京理工大学出版社, 2008: 111-112.

[2]陈慧敏, 栗苹, 闫晓鹏, 等. 基于不同作用体制的激光引信探测技术 [J]. 光学技术, 2006, 32(8): 348-350.

[3]蔡克荣, 邓甲昊, 王克勇. 小口径激光近炸引信的抗干扰方法 [J]. 光电工程, 2011, 38(7): 36-41.

[4]诸德放, 李友, 胡克旭. 战术空地导弹激光引信目标识别方法研究 [J]. 弹箭与制导学报, 2006, 26(4): 326-332.

[5]诸德放, 李友, 曾建新. 爆破式空地反辐射导弹引战配合 [J]. 弹道学报, 2007, 19(2): 21-24.

[6]张真, 马登武, 诸德放. 破片式空地反辐射导弹引战配合研究 [J]. 弹道学报, 2011, 23(4): 47-51.

[7]高建军. 空地导弹常规战斗部概览 [J]. 飞航导弹, 2008, 38(10): 54-57.

[8]谷良贤, 温炳恒. 导弹总体设计原理 [M]. 西安: 西北工业大学出版社, 2004: 217-224.

[9]谢邦荣, 尹健, 宋劲松. ARM导弹对雷达目标的毁伤概率仿真建模 [J]. 系统仿真学报, 2004, 16(9): 2044-2047.

收稿日期:2014-04-26

作者简介:诸德放(1962-),男,江苏高淳人，副教授,硕士,研究方向:武器系统与运用工程研究。

中图分类号:TJ439.2

文献标志码:A

Target Recognition Method of Laser Proximity Fuze for
Anti-radiation Missile

ZHU Defang1,ZHANG Zhen2,WANG Wenqiang3

(1Air Force Logistics Institute, Jiangsu Xuzhou 221000, China;2No.93033 Unit, Shenyang 110000, China;

3No.93069 Unit, Liaoning Pulandian 116200, China)

Abstract:To enable laser proximity fuze of anti-radiation missile(ARM) to detect and recognize radar targets, a detection and recognition method put forward based on multi-beam narrow laser light additionally, a mathematical model established change in distance measured by laser fuze to recognize targets’ height and width. By calculating Lebesgue integral of target occurring probability distribution function, the optimal light beam angle achieved, which maximize the detection probability with a fixed light beam number. Besides, typical munitions-target encounter simulation carried out. The result shows that the detection probability increases with decreas of ARM trajectory angle and of the height of target antenna, and the optimal light beam angles are dense in the middle of detection plane and spare in the edge.

Keywords:anti-radiation missile; laser proximity fuze; target recognition; detection probability; error analysis; light beam optimization