质量矩拦截弹变质心执行机构运动分析*

姚春明,李小兵,吴博文,白瑞阳

(空军工程大学防空反导学院, 西安　710051)

质量矩拦截弹变质心执行机构运动分析*

姚春明,李小兵,吴博文,白瑞阳

(空军工程大学防空反导学院, 西安710051)

摘要:质量矩拦截弹通过驱动变质心执行机构改变导弹质心,进而改变其姿态角,从而实现对拦截弹的机动控制。文中从质量矩拦截弹的动力学问题入手,建立了非线性动力学模型,并对变质心执行机构运动情况进行了理论分析及仿真研究,分析研究了引入变质心执行机构对拦截弹带来的转动惯量、力矩和状态耦合的影响情况,对影响拦截弹快速响应以及耦合特性的主要因素进行了分析,并进行仿真验证,为研究质量矩拦截弹的控制律和实际应用打下基础。

关键词:质量矩拦截弹;执行机构;运动分析

0引言

质量矩控制通过改变导弹内部质量块的位置来改变拦截弹的质心位置,进而对拦截弹的姿态进行控制[1]。与气动舵控制方式相比,它的执行机构位于导弹的内部,可以保证导弹良好的气动外形不被破坏;利用变质心执行机构移动改变拦截弹的姿态,进而产生配平力矩,只需微小移动质量块就能获得较大的控制力[2]。

尽管变质心控制方法有很多优点,但由质量块移动带来的系统非线性、耦合性以及导弹在飞行过程中气动参数、质量参数、结构总体参数和变质心执行机构参数的不确定性,使得其变得复杂。文中针对质量矩拦截弹的动力学问题,建立了动力学模型,通过对执行机构各参数的理论分析以及仿真研究,对影响其响应特性、自身力学特性以及耦合特性进行分析,验证了变质心执行机构参数对弹体姿态改变能力的影响,为进一步研究质量矩拦截弹的控制规律打下基础。

1动力学方程的建立

文中的研究对象是质量矩拦截弹,拦截弹内部的质量块分为沿导弹纵轴的一个质量块和垂直于导弹纵轴的两个质量块,可以控制导弹的攻角、侧滑角和滚转角3个通道的变化规律。

1.1　坐标系定义

1)随导弹运动的平动坐标系Axyz:设该坐标系坐标原点取导弹质心A,Ax轴为水平方向平行于Ox轴,Ay轴为导弹发射平面的另外一条轴平行于Oy轴,Oz轴根据右手定则得到。

2)速度坐标系Axvyvzv:该坐标系的坐标原点为导弹质心A,Axv轴为与导弹实时速度方向一致,Ayv轴沿弹体对称平面向上垂直于Axv,Azv根据右手定则得到。

地面坐标系、弹体坐标系与经典坐标系定义一致,在此不再赘述。

1.2　质量矩拦截弹运动学和动力学模型的建立

设质量矩拦截导弹的弹壳质量为mB,在导弹弹体坐标系中沿导弹纵轴Ax1方向的质量块的质量为m1,沿垂直于导弹纵轴的Ay1的质量块的质量为m2,沿垂直于导弹纵轴的Az1的质量块的质量为m3,导弹整体质量为mc,那么有:

可以定义无量纲参数质量比如下:

定义弹壳质心处所受的气动力为:

设三滑块在导弹弹体坐标系下的坐标分别为:

(1)

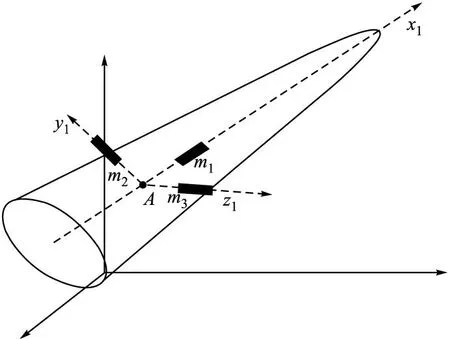
图1　弹体结构图

由图1可以看出质量块的初始位置分别为δx10、δy10、δz10,在对拦截弹实施姿态控制的过程中,滑块的移动位移分别是δx1、δy1、δz1。

拦截弹弹体相对于弹体坐标系的旋转角速度为:ω1=[ωx1ωy1ωz1]T。

对于三质量块控制的拦截弹,它的转动惯量为:

(2)

空气动力力矩为:

(3)

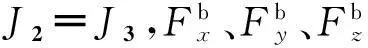
则拦截弹绕弹体各轴的转动方程为:

(4)

则质量矩拦截弹的姿态运动方程为:

(5)

(7)

2动力学分析

由第1.2节建立的拦截弹运动学和动力学模型可以看出,由于变质心执行机构的增加,在气动外形简化的同时,控制过程变得复杂,质量块的移动引起附加转动惯量和附加控制力矩,质量块之间的耦合运动以及状态耦合使得控制器的设计变得异常复杂,变质心执行机构的安装位置对拦截弹的质心位置影响也直接关系到拦截弹的静稳定性,因此质量矩拦截弹动力学分析显得极其重要[4]。

由于文中研究的是质量矩拦截弹变质心执行机构的动态特性对拦截弹姿态状态的影响,所以可以视拦截弹的初始扰动、气动不对称和仪器误差为理想状况[5]。

2.1　附加转动惯量分析

与传统气动舵控制拦截弹不同的地方在于质量矩拦截弹属于典型的多刚体系统,由第1.2节式(2)可以看出,在质量块移动的同时,整个拦截弹系统的转动惯量都会发生变化,而且转动惯量的变化是和控制力成二次方关系的。质量矩拦截弹执行机构的安装位置会影响拦截弹的质心位置,进而对拦截弹的静稳定性和控制效率影响很大。

把式(2)展开可以得到全弹转动惯量:

(8)

(9)

可得径向质量块运动引起惯性主轴的变化,在径向质量块不对称的移动方式下,转动惯量矩阵会产生相互耦合,同时,转动惯量是控制量的函数,使控制系统的设计变得复杂。

2.2　附加力矩分析

与传统气动舵控制的拦截弹相比,质量矩拦截弹利用变质心执行机构产生的力矩对拦截弹进行姿态控制,如何在质量块移动的过程中,以最小的移动位移和合理的移动加速度产生足够的控制力矩显得非常重要。

拦截弹所受的气动力矩为:

(10)

由于质量块运动产生的附加控制力矩为:

(11)

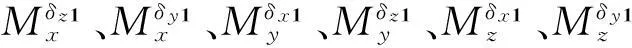
2.3　耦合特性分析

从第1.2节中拦截弹动力学模型可以看出,某一个质量块的移动会对拦截弹的3个方向的姿态都会产生作用,某一个姿态角速度的变化也同时会影响其他姿态状态的改变,这就是所说的控制耦合,如何削弱耦合是控制器设计的关键。

为了分析拦截弹飞行的动态耦合,在一定高度和一定速度及无控状态下来看其耦合特性。

3仿真验证

为验证质量矩拦截弹的动力学特性,在Matlab/Simulink平台上建立质量矩拦截弹非线性动力学模型,拦截弹飞行模型参数选择如下:拦截弹飞行速度为1 250 m/s,高度15 km,拦截弹的质量为160 kg,三质量块的质量分别为20 kg、10 kg、10 kg,三导轨的设计长度分别为0.3 m、0.18 m、0.18 m。仿真对比结果如图2~图4所示。

以轴向滑块为例,若滑块按照同一方向运动,一段距离之后就会静止,尽管可以产生较大的操纵力矩,但却不能使拦截弹在相应姿态调整后迅速回归平衡。可见滑块的阶跃移动是不符合实际应用规定的,因此文中考虑滑块进行交变运动,即在同一导轨轴线上往复运动。

以拦截弹Ay1轴转动惯量为例,取滑块m1的运动规律为δx1=Axe-a1tsin(ωt)[6],给出无阻尼时δx1=0.15sint和有阻时δx1=0.15e-0.6tsint的转动惯量曲线如图2,可得,当滑块进行无阻尼运动时,转动惯量成周期变化,不能稳定,在阻尼运动时,转动惯量很快衰减至转动惯量主轴上来,可见忽略执行机构运动产生的转动惯量影响是可行的。

图2　绕Ay1转动惯量变化曲线

以拦截弹俯仰通道力矩为例研究其力矩变化规律,对拦截弹分别进行无控制输入仿真和三滑块分别作为控制输入仿真[7],滑块在运动过程中运动规律均为δ=Ae-a1tsin(ωt),其中参数为Ax=0.15,Ay=Az=0.09,图3为力矩变化曲线。

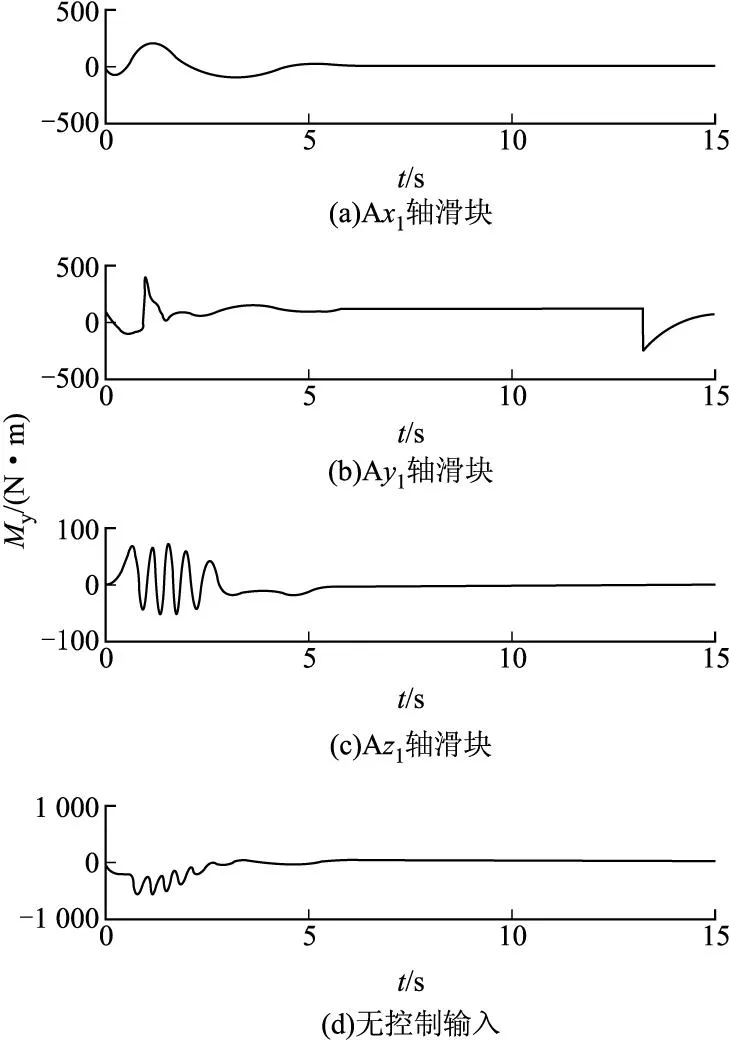
图3　俯仰通道力矩变化曲线

由图3可看出,Ax1和Ay1轴滑块移动产生的力矩较大,且Ax1轴滑块能产生稳定力矩,Ay1轴滑块不能产生稳定控制力矩,Az1轴滑块产生力矩较小,当3个滑块同时作用时,可以产生较大的且稳定的控制力矩。偏航和滚转通道的研究方法与此相似,不再赘述。

以俯仰角速率为例研究状态耦合情况,当输入为δ=Ae-a1tsin(ωt)(Ax=0.15,Ay=Az=0.09)时,验证以下4种情况时俯仰角速率变化情况:ωx=ωy=ωz=0;ωx=5rad/s,ωy=ωz=0;ωx=ωz=0,ωy=5rad/s;ωx=ωy=0,ωz=5rad/s。

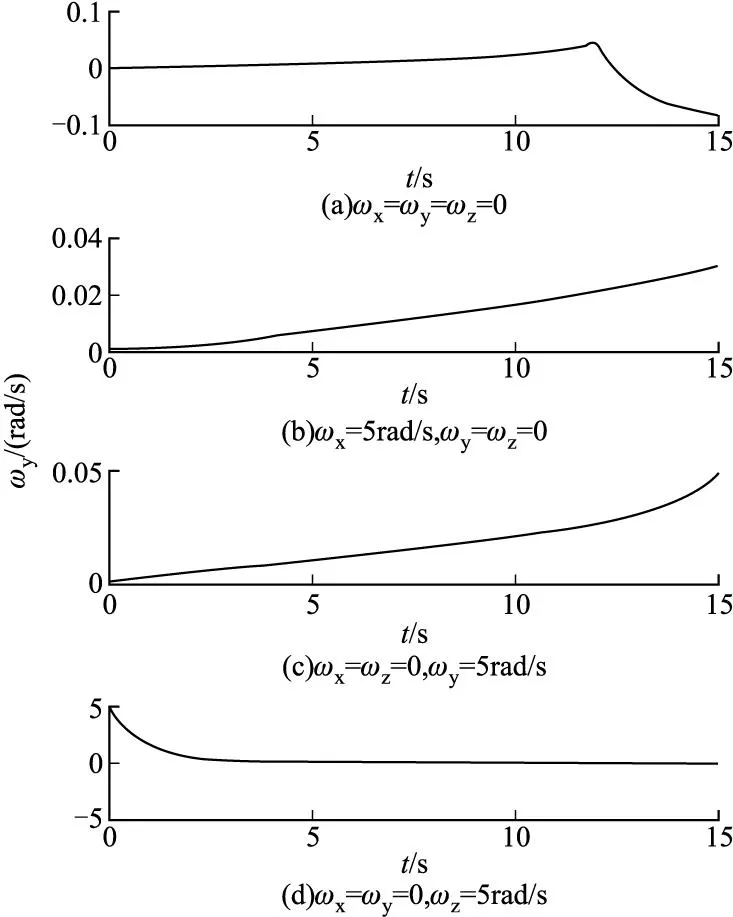
图4　ωy耦合变化曲线

从图4可以看出质量矩拦截弹各通道之间存在耦合,尤其是偏航角速率和俯仰角速率对其他通道的角速率影响较大,具有强耦合性。

4结论

文中研究表明:质量矩拦截弹的变质心执行机构对弹体转动惯量、控制力矩影响较大,特别是在执行机构无阻尼运动时,拦截弹成不稳定状态,表明质量矩控制技术在拦截弹上的运用仅适用于短时间姿态调整,不易进行过程控制,同时,执行机构在控制拦截弹姿态的过程中,必须协调控制才能保证控制稳定,且可得该型拦截弹状态耦合严重,在进行拦截弹控制器设计时必须考虑其耦合性。

参考文献:

[1]Robinett R D, Sturgis B R, Kerr S A. Moving mass trim control for aerospace vehicles [J]. Journal of Guidance, Control and Dynamics, 1996, 19(5): 1064-1070.

[2]Menon P K, Sweriduk G D, Ohlmeyer E J, et al. Integrated guidance and control of moving-mass actuated kinetic warheads [J]. Guidance, Control and Dynamics, 2004, 27(1): 118-126.

[3]Byme R H, Robinett R D, Sturgis B R. Moving mass trim control system design, AIAA-96-3826 [R]. 1996.

[4]徐国民, 李天舒, 张晓宇, 等. 质量矩控制导弹的建模与运动分析 [J]. 哈尔滨工程大学学报, 2011, 32(12): 1588-1593.

[5]高长生, 张研, 魏鹏鑫, 等. 质量矩控制自旋弹弹体性能分析 [J]. 飞行力学, 2013, 31(1): 61-64.

[6]廖国宾, 于本水, 杨宇光. 质量矩控制技术的机理分析及方程简化研究 [J]. 系统工程与电子技术, 2004, 26(11): 1635-1639.

[7]易彦, 周凤岐, 余松煜. 变质心控制导弹的稳定性分析与鲁棒控制 [J]. 上海交通大学学报, 2003, 37(4): 570-573. R D, Sturgis B R, Kerr S A. Moving mass trim control for aerospace vehicles [J]. Journal of Guidance, Control and Dynamics, 1996, 19(5): 1064-1070.

[2]Menon P K, Sweriduk G D, Ohlmeyer E J, et al. Integrated guidance and control of moving-mass actuated kinetic warheads [J]. Guidance, Control and Dynamics, 2004, 27(1): 118-126.

[3]Byme R H, Robinett R D, Sturgis B R. Moving mass trim control system design, AIAA-96-3826 [R]. 1996.

[4]徐国民, 李天舒, 张晓宇, 等. 质量矩控制导弹的建模与运动分析 [J]. 哈尔滨工程大学学报, 2011, 32(12): 1588-1593.

[5]高长生, 张研, 魏鹏鑫, 等. 质量矩控制自旋弹弹体性能分析 [J]. 飞行力学, 2013, 31(1): 61-64.

[6]廖国宾, 于本水, 杨宇光. 质量矩控制技术的机理分析及方程简化研究 [J]. 系统工程与电子技术, 2004, 26(11): 1635-1639.

[7]易彦, 周凤岐, 余松煜. 变质心控制导弹的稳定性分析与鲁棒控制 [J]. 上海交通大学学报, 2003, 37(4): 570-573.

收稿日期:2014-05-19

基金项目:航空科学基金(20130196004)资助

作者简介:姚春明(1988-),男,湖北丹江口人,硕士研究生,研究方向:导航、制导与控制。

中图分类号:V448.2

文献标志码:A

Motion Analysis on Mass Servo System of Moving Mass
Interception Missiles

YAO Chunming,LI Xiaobing,WU Bowen,BAI Ruiyang

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

Abstract:The’s mass-center changes with mass motion, and then the attitude angles change, thereby; the missile could be controlled to attack target. A coupled nonlinear system equations proposed based on the characteristics of the dynamics, with the analysis of the mass servo system, inertia moment and the coupling of the states researched. A series of simulation aboutmissile attitude performed so as to lay a foundation developing the control mechanism and application of the missiles.

Keywords:moving mass; mass servo system; motion analysis