基于新的几何算法的多无人机多威胁航迹规划*

赵均伟,孙吉良,孙伟奇

(1　海军航空工程学院,山东烟台　264001;2　海军航空工程学院航空训练基地训练部,山东青岛　266108;

3　海军航空工程学院青岛校区,山东青岛　266041)

基于新的几何算法的多无人机多威胁航迹规划*

赵均伟1,孙吉良2,孙伟奇3

(1海军航空工程学院,山东烟台264001;2海军航空工程学院航空训练基地训练部,山东青岛266108;

3海军航空工程学院青岛校区,山东青岛266041)

摘要:针对多无人机超低空突防的航迹规划问题,在分析约束条件和假设下简化为水平航迹平面规划。通过证明几何最短路径定理,研究单威胁情况下考虑最小转弯半径和攻击方位角限制下的最短航迹并计算导航点。其次讨论了突发威胁情况的航迹规避与调整,考虑多威胁圆重叠情况下的导航点坐标的推导,提出了一种新的多威胁规避最短切线逆推航迹规划几何算法,最后仿真验证该算法用于求解多威胁圆航迹规划问题的合理性和有效性。

关键词:航迹规划;几何算法;切线逆推;UAV;低空突防;多威胁圆

0引言

王庆江等在文献[1]中提出了在无威胁情况下路径规划的一些基本约定的基础上,重点研究了基于几何原理任意两点间的无人机路径规划法的基本思想。并给出了路径规划的主要步骤。但是没有考虑存在威胁情况。周代忠等在文献[2]中提出了圆切线几何算法,克服传统可行方向法容易陷入局部极小点的缺陷,但是直接把圆切线的切点作为下一个航迹点,所规划的航迹有可能落入威胁圆边界内,不是一条十分安全的航迹,也没有给出最短路径的证明。张友安等在文献[3]中提出一种多威胁规避算法,可以实现在一定的假设条件下,从目标点开始,按照反方向依次逆推至初始点,从而求得参考航迹。其算法未充分考虑威胁区域的分布情形,因而存在一定的缺陷。彭华等在文献[4]中对多威胁规避算法进行了改进,具有实现复杂情形下的路径规划能力,但是所规划的路径还不是最短的。

综合参考以上文献,汲取文献中提出算法的优点,克服原有算法的缺点,结合航迹规划问题的特点和各种约束,提出了一种新的多威胁规避最短切线逆推航迹规划几何算法求解多威胁下UAV航迹规划问题。

1几何法的基础

1.1　航迹规划的约束

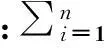
1.2　问题假设

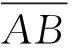
1.3　典型几何定理和推论

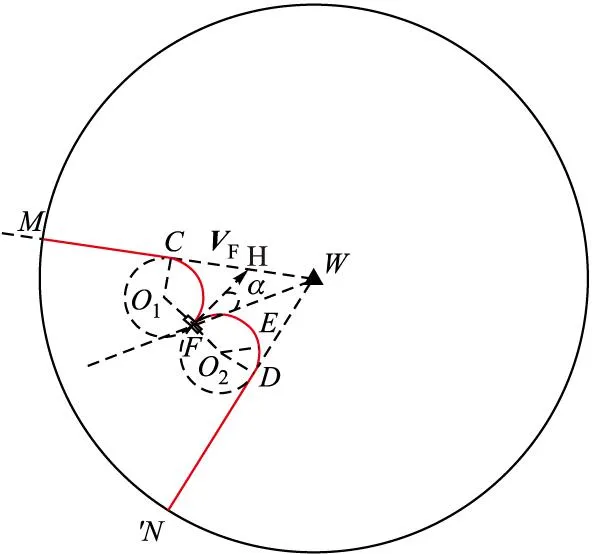
图1　最短距离规避航迹

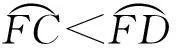
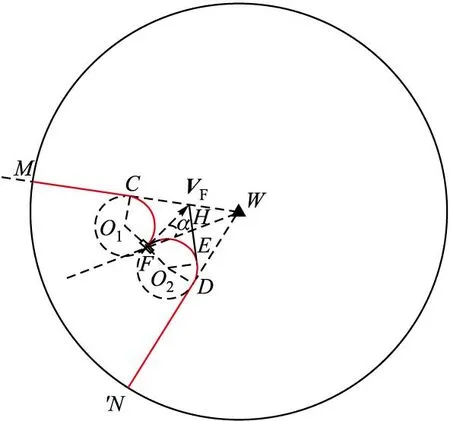
图2　最短距离规避航迹辅助线作法

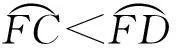
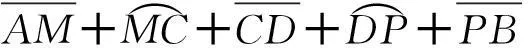
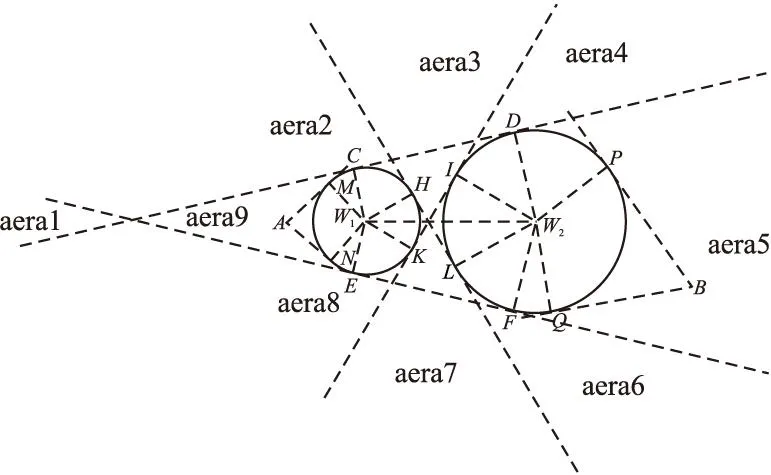
图3　两威胁区规划空间区域划分图

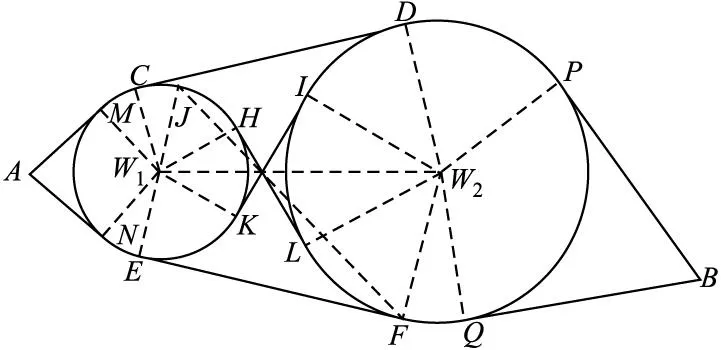
图4　定理2中线段和弧位置示意图

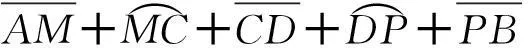
推论1结论显然成立,在此不做证明。定理2中当起始点和目标点在其他区域时处理方法类似,由定理2可推广到多威胁圆的情形下最短路径的证明。

2基于几何法的航迹规划

2.1　针对突发威胁的航迹规避

当UAVF在飞行的航迹上发现突发威胁源W时,判断UAV位置F与威胁圆圆心W的距离,可分成以下几种情况分别处理:

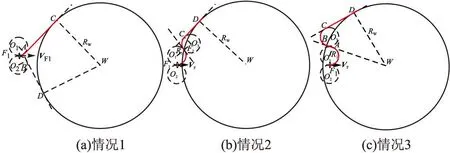
图5　情况1、情况2、情况3规避路径策略图

2.2　单威胁情况下航迹规划

假设UAV的初始位置为F1,速度矢量为VF,最小转弯圆半径为R1,单威胁圆的圆心为W,半径为RW,目标位置为T,目标进入方位角为θ,UAV以目标进入角进入目标攻击区域时离目标最小距离为R3,表明UAV必须在离目标T距离R3附近完成攻击方位的调整,其实R3≫R1,RW≫R1,R1相对于R3、RW可忽略不计,为了图示方便故将R1放大。则单威胁规避情况下航迹规划如图6所示。

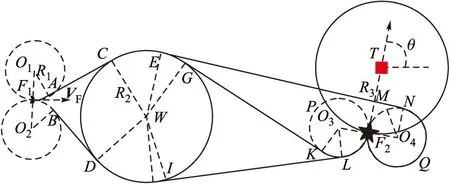
图6　UAV横侧向运动单威胁水平航迹平面路径规划图

共有四种航迹的规划方案,分别是:

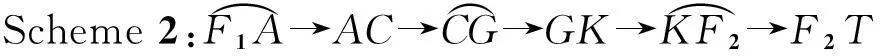
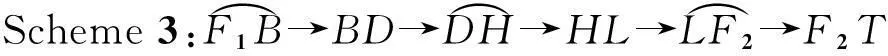
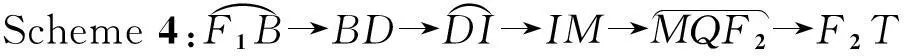
路径长度与无人机的耗油量、飞行时间成正比,最优的路径规划方案可设为最短路程长度对应的方案,则航迹规划问题可表示为:

各直线段长度和弧长计算公式推导如下:

假设起始点F1坐标为(xF1,yF1),速度矢量VF与x轴正半轴的夹角为φ,设最小转弯圆的圆心O1坐标为(x1,y1),O2坐标为(x2,y2),半径为R1,则直线O1O2的斜率为-cotφ,O1、O2点的坐标可由以下联立方程组:

求得:

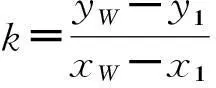
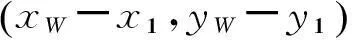
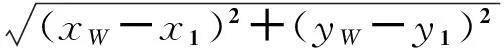
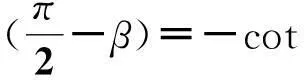
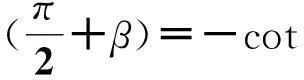
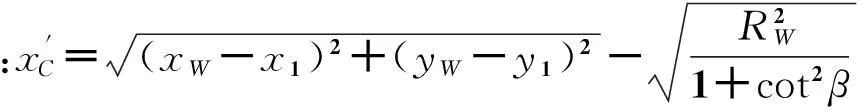
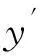
将切点A、C坐标还原,先进行坐标旋转变换,即:

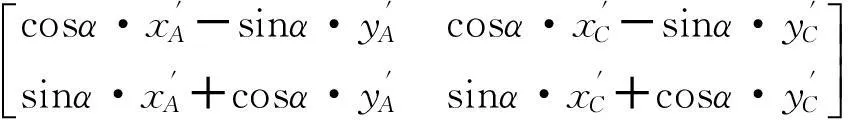
再进行坐标系平移,则可得原坐标系下的A、C坐标分别为:

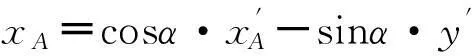
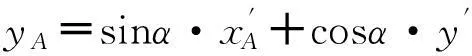
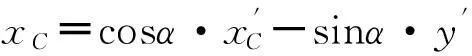
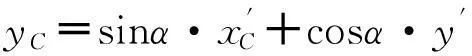
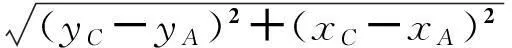
2.3　多威胁情况下航迹规划

多威胁规避最短切线逆推UAV航迹规划几何算法主要思想是从起始点到目标点作一条理想航线,然后判断理想航线上的威胁个数,没有和理想航线相交的威胁暂时认为对UAV不构成威胁,这样处理的好处是减少了数据的判断量,提高了航迹规划实时性。

该几何算法示意图如图7所示,首先求距离目标点最近的相交威胁圆或各重叠威胁圆并作切线,通过单威胁规避法求出两新的导航点E和D,判断与理想航线夹角最小的切线且该切线不与其他威胁相交,作为选定的切线航段EP2和航迹点E。以该切点E作为下一规划航段的起始点,再从起始点到航迹点E作一条直线,求距离E点最近的相交威胁圆或各重叠威胁圆,求取航迹点E所在威胁圆与相交威胁圆或各重叠威胁圆的内外切线,在相交威胁圆或各重叠威胁圆上的切点分别为H和G,在航迹点E所在威胁圆上的切点分别为M和F,分别判断线段HM与P1M,GF与P1F夹角最小的切线GF,且该切线不与其他威胁相交,作为选定的切线航段。以该切点F作为下一规划航段的起始点,并求与直线FP2相交的威胁圆或各重叠威胁圆,如果没有与F点所在威胁圆以外相交的威胁圆,则将F点看作目标点重复上述方法,直到规划到起始点。如果有其他相交的威胁圆,则将F点看成起始点重复上述方法,直到规划到目标点。

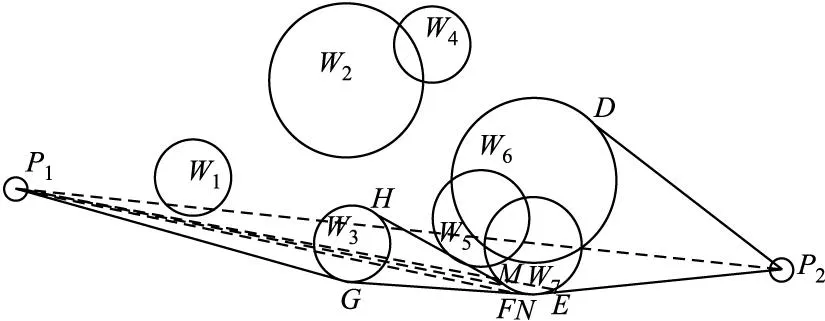
图7　多威胁复杂情况航迹规划威胁规避算法图

从目标点向起始点逆推多威胁规避几何算法的流程框架如图8所示。

图8　多威胁规避逆推几何算法流程图

2.4　多UAV多方位攻击航迹规划

针对目标进行多方位协同攻击多无人机航迹规划,与单无人机航迹规划类似,只是在无人机调整攻击方位角时,把调整距目标的最短距离限制看成一个以目标为圆心,以最短距离为半径的威胁圆。无人机不能进入该区域调整航线,多无人战斗机多方位攻击航迹规划示意图如图9所示。

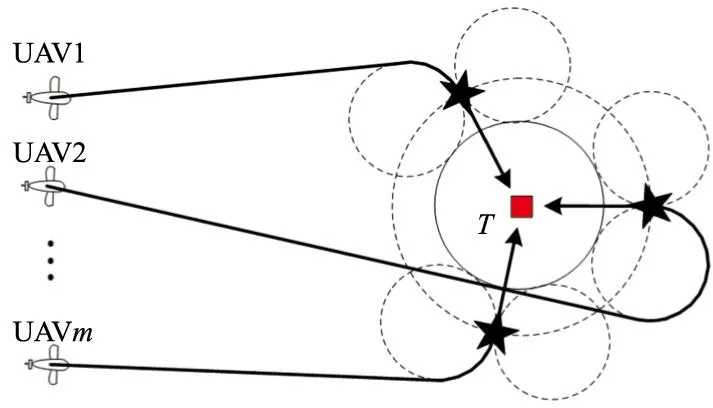
图9　多无人战斗机多方位攻击航迹规划示意图

3仿真分析

假设UAV最小转弯半径相对于威胁圆半径和离目标最小距离来说可以忽略不计。分别针对单威胁规避、多威胁规避和多UAV协同多方位攻击进行航迹规划仿真。

3.1　单威胁规避算法仿真:

UAV起始点位置坐标为(100 km,250 km),目标点位置坐标为(500 km,80 km),威胁圆圆心横、纵坐标和半径分别为(280 km,200 km,100 km),目标进入方位角θ=45°,以目标进入角进入目标攻击区域时离目标最小距离为40 km。单威胁规避算法仿真结果如图10所示。从图10中可以看出,得到的航迹可以有效的规避单威胁区域选择最优路径达到目标点。

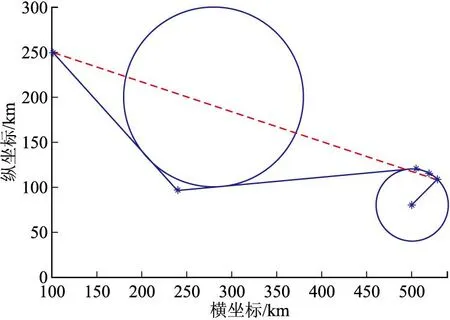
图10　单威胁规避算法仿真

3.2　多威胁规避算法仿真

UAV起始点位置坐标为(100 km,250 km),目标点位置坐标为(500 km,80 km),威胁圆各圆心横、纵坐标和半径分别为(150 km,230 km,30 km)、(300 km,110 km,20 km)、(400 km,130 km,55 km)、(250 km,160 km,30 km)、(300 km,200 km,30 km),目标进入方位角θ=225°,以目标进入角进入目标攻击区域时离目标最小距离为40 km。多威胁规避算法仿真结果如图11所示。从图11中可以看出,得到的航迹可以有效的规避多威胁区域选择最优路径达到目标点。

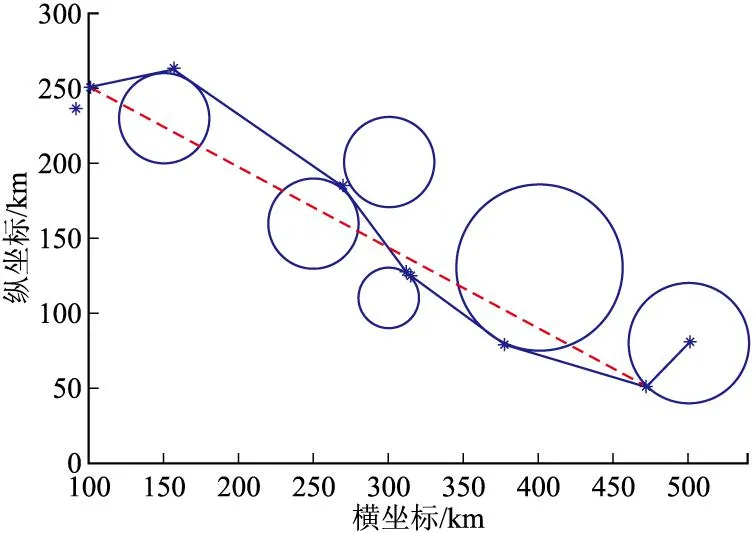
图11　多威胁规避算法仿真结果

3.3　多UAV多方位协同攻击航迹规划仿真

UAV1起始点位置坐标为(100 km,250 km),目标进入方位角θ=45°。UAV2起始点位置坐标为(100 km,150 km),目标进入方位角θ=225°。UAV3起始点位置坐标为(100 km,0 km),目标进入方位角θ=315°。目标点位置坐标(500 km,80 km)。威胁圆各圆心横、纵坐标和半径分别为(150 km,230 km,30 km)、(300 km,160 km,20 km)、(400 km,130 km,55 km)、(250 km,170 km,30 km)、(300 km,200 km,30 km)、(300 km,100 km,25 km)、(220 km,30 km,35 km)、(350 km,50 km,35 km)。以目标进入角进入目标攻击区域时离目标最小距离为40 km。多UAV协同多方位攻击航迹规划仿真结果如图12所示。从图12中可以看出,多UAV都规避威胁区域对目标实施多方位攻击。

图12　多UAV多方位协同攻击协同航迹规划仿真结果

4结论

文中针对UAV对水面舰艇实施超低空突防攻击的几何航迹规划问题,考虑飞行器的法向加速度限制和攻击方位角限制进行横侧向运动水平航迹平面路径规划。在算法研究基础上,对算法进行了改进,摈弃以往以相交威胁圆个数多少来决定最短切线的方法,采用与理想航迹(两点之间连线)夹角最小作为切线和航迹点选择的依据,并且在此基础上使路径能沿着威胁圆的圆弧行进,该多威胁规避算法求得的路径并被证明为最短路径。

这种方法构造出来的航迹几乎接近威胁,其缺点是在无人机飞行过程中出现位置偏差就很容易被发现。同时,该方法基于确定的环境模型而开展的。在实际作战时,由于战场环境的复杂性和多变性,很难获得精确的战场环境模型。因此,针对复杂多变的战场环境,如何提高运动规划方法的环境适应性还需要作进一步的研究。

参考文献:

[1]王庆江, 高晓光, 符小卫. 无威胁情况下任意两点间的无人机路径规划 [J]. 系统工程与电子技术, 2009, 31(9): 2157-2162.

[2]周代忠, 张安, 陶勇. 无人战斗机航路规划圆切线算法 [J]. 火力与指挥控制, 2007, 32(3): 49-51.

[3]张友安, 范作娥, 糜玉林. 反舰导弹航路规划与威胁规避算法 [J]. 吉林大学学报: 工学版, 2008, 38(3): 746-752.

[4]彭华, 许斌, 罗灿华. 一种基于几何方法的人员疏散多威胁规避路径规划算法 [J]. 建筑科学, 2010, 26(3): 84-86.

[5]Ren W, Chao H, Bourgeous W, et al. Experimental validation consensus algorithms for multivehicle cooperative control [J]. IEEE Transactions on Control System Technology, 2008, 16(4): 745-752.

[6]郗永军, 周德云. 多无人机协同攻击路径规划研究 [J]. 计算机仿真, 2010, 27(3): 69-72.

[7]张煜, 张万鹏, 陈璟, 等. 基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划 [J]. 航空学报, 2011, 32(7): 1240-1251.

[8]刘钢, 老松杨, 谭东风, 等. 反舰导弹航路规划图形化快速逆推方法 [J]. 弹道学报, 2011, 23(2): 52-56.

[9]丁伟峰, 严建钢, 叶文. 不同作战任务条件下UCAV航路规划问题建模 [J]. 海军航空工程学院学报, 2012, 27(1): 115-119.

[10]杨俊, 朱凡, 张健, 等. 复杂环境下无人机快速航迹规划研究 [J]. 计算机工程与应用, 2012, 48(21): 225-229.

[11]刘铭, 徐杨, 陈峥, 等. 基于Multi-Agent系统的多飞行器协同路径规划方法的研究 [J]. 计算机科学, 2012, 39(1): 219-222.

[12]吴文超, 黄长强, 宋磊, 等. 不确定环境下的多无人机协同搜索航路规划 [J]. 兵工学报, 2011, 32(11): 1337-1342.

[13]韩攀, 陈谋, 陈哨东, 等. 基于改进蚁群算法的无人机航路规划 [J]. 吉林大学学报: 信息科学版, 2013, 31(1): 66-72.

[14]梁宵, 王宏伦, 曹梦磊, 等. 无人机复杂环境中跟踪运动目标的实时航路规划 [J]. 北京航空航天大学学报, 2012, 38(9): 1129-1133.

收稿日期:2014-04-24

作者简介:赵均伟(1984-),男,浙江仙居人,助教,博士研究生,研究方向:任务规划。

中图分类号:V218

文献标志码:A

Multi-threat Path Planning of Multi-UAV Based on New Geometric Method

ZHAO Junwei1,SUN Jiliang2,SUN Weiqi3

(1Naval Aeronautical and Astronautical University, Shandong Yantai 264001, China;

2Training Department of Aviation Training Base，Naval Aeronautical and Astronautical University, Shandong Qingdao 266108, China;

3Qingdao Campus， Naval Aeronautical and Astronautical University, Shandong Qingdao 266041, China)

Abstract:In view of path planning problem of multiple unmanned aerial vehicle (UAV) hedgehopping penetration, it can be simplified to only consider UAV lateral movement level route planning. In the analysis of route planning constraints and under the problem assumption, the theorem of geometric shortest path was proved, focused on single threat situation, considering minimum turning radius and attack angle constraints, the shortest route of target attacking and the navigation point was calculated. route elusion and adjustment for sudden threat were discussed. Under the threat circles overlap cases, navigation coordinate deduction was studied. For route planning problem of multiple threats, a new trajectory planning geometric algorithm was proposed by the shortest tangent recursion method for avoidance of multiple threat circles. The simulation results verify rationality and validity of the new algorithm.

Keywords:path planning; geometric method; tangent backstepping trajectory; UAV; low altitude penetration; multiple-threat circle