天然次生林直径分布的研究

天然次生林直径分布的研究

王砚峰，王鹤智

(国家林业局调查规划设计院，北京 100714)

摘要该研究应用东北林区调查的119天然林标准地数据，通过绘制各林分直径分布直方图，分析林分的直径分布规律，运用SB分布、指数分布、正态分布、Weibull分布和β分布函数对其进行拟合，建立直径回归模型，并采用矩解法求解参数，更精确地比较各种分布函数对实际数据的拟合效果。研究结果表明：林木株数随着直径的增大呈减少的趋势；指数分布和Weibull分布的拟合效果较好，但指数分布优于Weibull分布。观察指数分布函数的各参数的变化规律，发现参数a基本不变，而参数b在变化。绘制参数b与林分调查因子间的散点图，发现指数分布中的参数b与林分平均直径有显著的相关性。通过相关性分析，选择函数进行拟合，结果表明：幂函数的拟合效果最好，相关系数最高。通过对参数b的再参数化建立模型，最终得到最优的天然次生林林直径分布模型。

关键词天然次生林；直径分布；林分调查因子；林分直径

中图分类号S757

作者简介王砚峰(1978-)，男，山东荣口人，工程师，硕士，从事森林经理研究。

收稿日期2015-06-05

Study on DiameterDistribution of Natural Secondary Forest

WANG Yan-feng, WANG He-zhi (State Forestry Bureaue Survey Scheme Designing Institute, Beijing 100714)

AbstractUse SB distribution function, exponential distribution function, normal distribution function, Weibull distribution function and beta distribution function to fit the transformation regularities, set up parameter regression model. In order to compare various distribution function of the actual data fitting effect more precisely, the solution method using torque. Research results show: the rule of diameter distribution is that with the increasing of the diameter, the number of trees is reduced; the fitting effects of exponential distribution and Weibull distribution are good, but the exponential distribution is better.Observing each parameter variation of exponential distribution function, it can be seen that parameter a is constant while parameter b is changing. By making chat between parameter b and stand description factor, it shows that parameter b and average diameter has significant correlation. Through the correlation analysis, select the appropriate functions to fit them. The results show that the power function fits best, the correlation coefficient is the highest. Combining the relationship between parameter b and average diameter, obtain the general diameter distribution function of natural secondary distribution function.

Key wordsNatural secondary forest; Diameter distribution; Stand description factor; Stand diameter

对于林木的直径来说，其大小与林分的蓄积量存在着非常密切的关系，总体上来说对于林分结构的合理确定是充分发挥其各种效益的基础和条件[1-5]。因此，需要通过外业调查等方式获得林分结构的详细信息，充分掌握林木生长和退化的整个过程，从而对更加充分地了解林分竞争起到非常好的作用，同时也有利于充分发挥林分结构的各种特性和作用，为林分经营奠定基础[6-8]。

在通常条件下，需要对森林的直径结构进行合理的确定，在实践的基础上，需要合理地确定经营措施、制定主伐年龄[9]。林木直径代表了森林对于经营措施的综合反映，是一个综合体。因此，需要不断地通过外业调查来确定经营指标，从而为林分的正常生长提供好的条件和基础。当然，在目前条件下，不同的国家对于林分直径的确定方法也存在非常大的差异性，在调查方法上很难做到统一[10-13]。N·Nishimura[14]在早期的研究中，对日本温带地区阔叶树种的直径分布进行了研究，采用的方法是直方图，结果显示，日本温带地区的常绿阔叶林的直径总体上呈现双峰分布。但综合国内外的研究现状可以知道，目前对直径分布应用最多的还是Weibull分布，这是由于Weibull分布所有的参数具有非常大的灵活性，具有明显的生物学意义，能够对树木的生长等进行合理的描述和解释，能够进行科学的预估和评价。因此，这些年来，该分布得到了很多学者的广泛应用，也取得了非常大的成果。该研究应用在东北林区调查的119天然林标准地数据，通过绘制各林分直径分布直方图，分析林分的直径分布规律。

1 研究地概况及方法

1.1 研究地区概况及数据收集帽儿山实验林场位于我国黑龙江省哈尔滨市，距离哈尔滨市区仅有100 km左右。该地区的气候属于温带季风气候，非常干燥，冬季寒冷、时间长，夏季炎热、时间短，季节之间差别非常明显。帽儿山林场年均气温为2.8 ℃，年降水量为723.8 mm，主要集中在6～8月份。

穆棱林业局位于黑龙江省东南部地区，属于长白山地区的一部分，与老爷岭相邻，位于我国黑龙江省的西南部地区。地理坐标为129°46′55″～130°32′27″ E，43°49′57″～44°35′27″ N。穆棱林业局有8个林场。在整个黑龙江省来说，穆棱地区的气温稍微偏高，气候类型属于中温带大陆性季风气候，夏季干燥炎热，总是会出现很高的温度，但炎热持续的时间比较短暂。在该地区，降水时间主要集中在6～8月份。

为了使数据比较有代表性，在研究区域内不同立地条件下进行标准地的设置，对于标准地内的所有林木都要进行每木检尺，测定每株林木的胸径、树高、枝下高等林木因子。依据所有林木的测量情况进行标准木的选取。该研究所用数据来自于帽儿山林场和穆棱林场，其中包括帽儿山2007年调查的45块标准地和2008年调查的6块标准地以及穆棱2008年调查的68块标准地。

1.2研究方法

1.2.1直径分布模型。根据以往的研究成果，正态分布、指数分布、Weibull分布、β分布以及SB分布都在一定范围内得到了广泛的应用，对所有数据进行拟合和检验，对直径分布模型采用矩解法进行参数估计，个别异常点对参数拟合会造成很大的影响，会使模型产生离散，因此，参数估计之前把一些异常点都剔除。通过研究发现，Weibull分布和指数分布的通过率是非常大的，在该研究中选择4块标准地进行分析。

采用矩法估计对其进行研究：

(1)正态分布

正态分布的概率密度函数为：

(Ⅰ)

(2)Weibull分布

其概率密度函数为：

(Ⅱ)

式中：a为位置参数，一般指林分的最小直径Dmin；b为比度参数；c为形状参数；D为林木直径。

(3)β分布

其概率密度函数为：

(Ⅲ)

式中：a,b分别为径级的上限和下限；α,β为形状参数。

(4)SB分布

其概率密度函数为：

(Ⅳ)

而：

式中：ε为径级分布下限，ε=Dmin；λ为范围参数，λ=Dmax-Dmin；σ为峰度参数；γ为偏度参数。

(5)指数分布

二参数负指数分布概率密度函数为：

(Ⅴ)

式中：a为位置参数(直径分布最小径阶下限值)；b为尺度参数。

(Ⅵ)

1.2.2参数的再参数化。分别研究每一模型参数与数据的关系，选出最优的模型，分别探究各个参数的变化规律，通过描述其散点图进而探究其变化规律。因此，模型的再参数化是构建预估模型的一个过程。

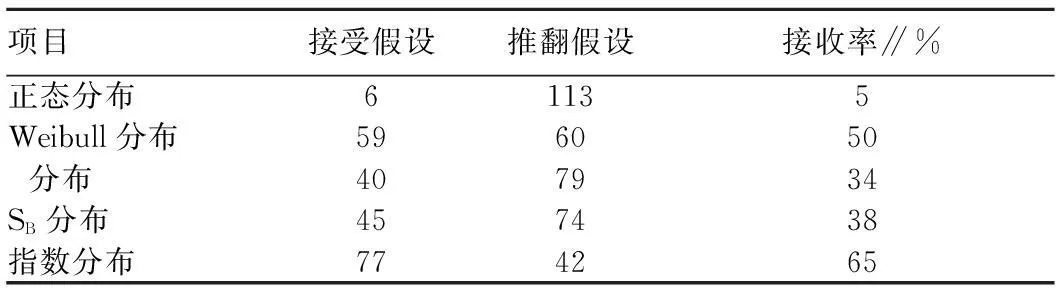
表1　各种分布函数拟合检验结果

2结果与分析

2.1直径分布各模型的拟合检验结果将5种函数对各样地直径分布拟合检验结果列于表1。通过对5种函数进行χ2检验，可以得出：指数分布和Weibull分布接收率较大，拟合较好。指数分布优于Weibull分布。部分样地的指数分布和Weibull分布拟合效果见图1～4。

2.2指数分布与林分调查因子间的关系由指数分布的数据处理结果(表2)可以看出：指数分布的2个参数a，b中，a的值(除YH-7外)均为5，只有b的值在变化，通过对b值与林分调查因子之间的散点图可知b值与林分平均直径(DG)相关性显著，而与其他因子均无明显的相关性。选择对数函数、指数函数、幂函数拟合b值和林分平均直径(DG)关系，拟合效果图(图5)和拟合结果如下：

对数函数：b=-0.151ln(DG)+0.536

(Ⅶ)

其中：R2=0.921 4。

指数函数：b=0.410 3e-0.080 5DG

(Ⅷ)

其中：R2=0.935

幂函数：b=5.671 2DG-1.141 5

(Ⅸ)

其中：R2=0.957 3

通过对图5分析可知：幂函数分布的参数b与林分平均直径的相关系数最大，拟合效果最优。又因为直径分布的指数函数为：f(D)=be-b(D-a)D>a，所以可得直径分布函数为：

f(D)=5.671 2DG-1.415exp(-5.671 2DG-1.415(D-5))，D>5

(Ⅹ)

式中：D为林木的胸径；DG为林分的平均直径。

3 结论

该研究利用帽儿山2007年调查的45块标准地和2008年调查的6块标准地以及穆棱2008年调查的68块标准地，选择5种直径分布函数进行拟合。

(1)该研究为了探究直径分布的规律，对数据进行非常详细的分析，对一些异常的数据进行了剔除。总体上，该文采用5种分布函数进行研究，这5个分布函数分别是指数分布、Weibull分布、SB分布、β分布和正态分布。结果表明，指数分布和Weibull分布都比较合适，但总体上指数分布的拟合效果比较好。

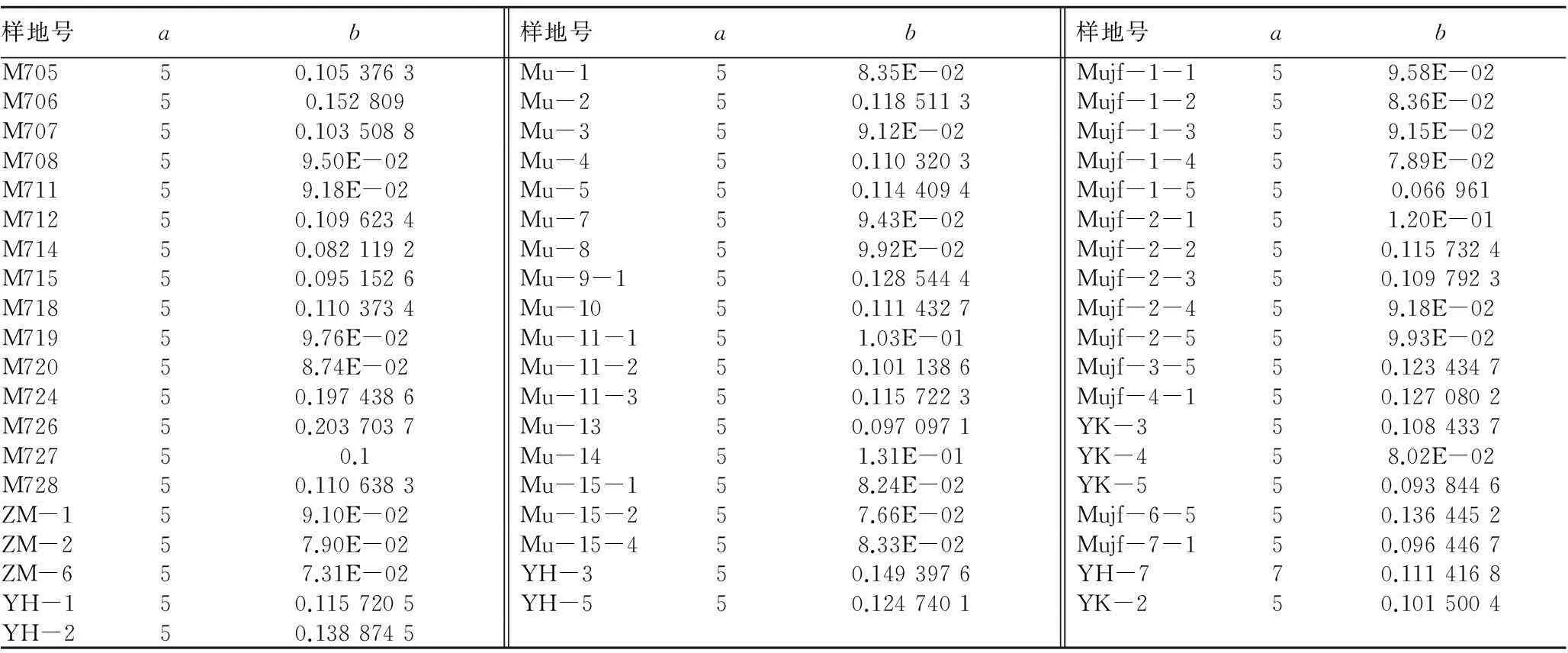
表2　指数分布拟合的参数 a、 b值

(2)在指数分布中，a值总体上不变，为5，只有参数b的数值会不断变化。

(3)对参数b与林分平均直径的散点图进行分析，分别选择对数函数、指数函数、幂函数进行分析，结果显示对数函数比较好。

参考文献

[1] 胡文力.长白山过伐林区云冷杉针阔混交林分结构的研究[D].北京：北京林业大学，2003.

[2] 李毅,孙雪新,康向阳.甘肃胡杨林分结构的研究[J].干旱区资源与环境,1994,8(3):88-95.

[3] 陈东来,秦淑英.山杨天然林林分结构的研究[J].河北农业大学学报,1994,17(1):36-43.

[4] 孟宪宇.测树学[M].北京:中国林业出版社,1996.

[5] SANNIKOVA N S.Microecosystem analysis of the structure and functions of forest biogeocenoses[J].Russian Journal of Ecology, 2003,34(2):80-85.

[6] 邵青还.第二次林业革命——“接近自然的林业”在中欧兴起[J].世界林业研究,1991,4(4):8-15.

[7] 沈国舫.现代高效持续林业——中国林业发展道路的抉择[J].林业经济,1998(4):1-8.

[8] 邵青还.德国的林业保护政策及其评价[C]//中国林业如何走向21世纪.北京:中国林业出版社,1995：53-60.

[9] 李芳东,李宗然,周道顺,等.兰考泡桐林分结构规律研究[J].林业科学研究，1996(2):114-120.

[10] 黄清麟.福建青冈萌芽林分结构及生产力的研究[J].福建林学院学报,1995,15(2):107-111.

[11] 陈昌雄,陈平留.闽北天然异龄林林分结构规律的研究[J].福建林业科技,1997,24(4):1-4.

[12] WAYAN C.Zipperer Species composition and structure of regenerated and remnant forest patches within an urban landscape[J].Urban Ecosystems,2002,6:271-290.

[13] CHOKKALINGAM U，WHITE A.Structure and spatial patterns of trees in old-growth northern hardwood and mixed forests of northern Maine[J].Plant Ecology,2001，156(2)：139-160.

[14] NISHIMURA N，HARA T，MIURA M.Tree competition and species coexistence in a warm-temperate old-growth evergreen broad-leaved forest in Japan[J].Plant Ecology,2002,164:235-248.