悬臂拼装桥主梁制造线形计算

2015-12-26张安林,郑报文,夏伟

安徽建筑大学学报 2015年1期

悬臂拼装桥主梁制造线形计算

张安林，郑报文，夏伟

(安徽省交通勘察设计院有限公司，安徽合肥230011)

摘要：斜拉桥悬臂拼装施工速度快、质量高、适应性强,这种施工方法在国内外已经广泛应用, 从而悬拼结构的施工线形控制问题开始凸现出来.为了使钢梁在安装过程中高质量对接并最终达到成桥线形,需将钢梁按制造线形在胎架上预拼. 以某钢箱梁斜拉桥为工程背景,用有限元分析软件midas建立该桥模型,通过零初始位移法和切线初始位移法分别计算主梁制造线形. 对安装新梁段与相邻旧梁段夹角从几何关系进行了推导证明,并据此给出了计算无应力制造线形的实用公式.

关键词：悬臂拼装；钢箱梁；施工控制；制造线形

收稿日期：2014-06-23

作者简介：张安林(1987-),男,硕士研究生, 主要研究方向为大跨度桥梁施工监控.

中图分类号：U448.28

Computation of Fabrication Profile of girders

in Cantilever Erection Practice of Bridges

ZHANG An-lin,ZHENG Bao-wen,XIA Wei

( Anhui Provincial Communications survey & Institute Co ,Ltd ,Hefei ,Anhui 230011)

Abstract:Cable-stayed Bridge with cantilever assembling, which have many advantages including fast construction, high quality and adaptability, has been widely used in the world. Profile control began to stand out in cantilever structure during construction. In order to make the steel beam docking in high quality during the installation process, and eventually reach the design profile, the steel girder need to pre-fight on the tire rack. A Cable-Stayed Bridge of steel box beam, which model was established used finite element analysis software Midas, was taken as engineering background, to elaborate how to calculate fabrication profile of main beam using Zero Initial Displacement Method and Tangent Initial Displacement Method. Angle relationship was derived through the geometric relationships between a new beam which will be installed and the adjacent old beam which has just been fixed, and Practical formula of Stress-free fabrication profile was given accord to the result.

Key words:cantilever erection; steel box girder; construction control; fabrication profile

1引言

当前国内众多桥梁采用悬臂施工方法,混凝土桥梁悬臂施工只需要提供正确的预拱度即立模标高即可,但是钢桥与混凝土桥悬臂施工最大的不同是钢梁段前端标高的调整受到顶底板焊缝宽度的限制,而混凝土桥梁则基本不受转角的限制,前端标高调整相对容易.这就要求在工厂制造钢梁的时候按事先计算好的制造线形中的角度进行预拼,保证各梁段最合适的顶底板长度, 从而保证钢梁之间有合适的缝宽。而制造线形的主要工作就是计算在无应力状态下的各梁段之前的夹角,本文对于其计算方法进行了推导证明。并详细介绍了由施工阶段结果恢复无应力制造线形的整个过程。

2工程背景

广州市南沙开发区第一标段凤凰一桥[1]是凤凰大道跨越蕉门水道,主桥全长272m, 左右完全对称,为2×136m独塔单索面混合梁斜拉桥,桥面全宽42.9m。主梁采用钢箱梁与混凝土箱梁相结合的混合梁,主塔中心线顺桥向两侧共28m范围采用预应力混凝土箱梁(0#块),其余部分为扁平闭口钢箱梁,每边12个梁段，一个D梁段，一个B2梁段，8个C梁段，一个B1梁段,一个A梁段。C为拉索梁段,B1为合拢段,A为边跨梁段，钢箱梁段与混凝土梁段采用钢-混结合段连接。主桥的钢箱梁全长244m,桥梁中线处梁高3.5m。钢箱梁标准节段长12m,最大吊装重量2185KN。

斜拉索在主梁上索距为12m,塔上索距为2m,斜拉索在塔上采用冷铸锚,在主梁上采用销接耳板式锚,全桥共设16根斜拉索,斜拉桥14#、16#过渡墩墩顶设置竖向支承纵向活动球形钢支座及横向限位支座,15#主墩为塔墩梁固结。桥型图及钢箱梁标准断面图如下图1～2：

该桥采用有限元软件Midas进行建模，施工过程模拟计算主要采用空间杆系模型，人字形主塔和主梁采用空间梁单元模拟，斜拉索采用只受拉空间杆单元模拟。0#块采用设计数值截面,而钢箱梁采用数值截面中的任意截面,均为在aotucad中将截面形状画出，然后导入midas，全桥模型共有189个单元，211个节点，活载为城A一级,钢梁自重,边跨压重,二期恒载均采用均布荷载模型,桥面吊机，吊装荷载采用集中力模拟，计算模型见下图3。

3制造线形计算

制造线形，工程中亦称预拼线形,是主梁在制造过程中零应力状态下的线形;悬臂拼装时，待安装梁段处于近似无应力状态[2],而已安装梁段处于自重、桥面吊机等荷载作用下,如果在悬臂安装阶段将相邻的已安装的梁段应力释放,则可恢复各个梁段之间的无应力关系,安装这种理念,可直接按施工阶段计算结果推算出无应力制造线形。下文中将具体介绍。

3.1零初始位移法

零初始位移法简称零位移法[3],就是将新安装单元除共用节点外的其他节点初始位移指定为零。而Midas的处理正是从单元生成的位置作为0位移位置，故按零位移法计算时,只需在该梁段焊接完成后(吊机未脱钩)将其结构组激活便可。由此我们也可以看出, 零位移法一般常用于线性分析[4],因为线形分析时任意施工阶段的单位坐标系均基于结构的初始建模位置,不会随着单位变形而改变。下面先从几何关系说明安装新梁段与相邻旧梁段夹角的计算方法。

如上图4,A,B代表①梁段安装位置,A2',B2'代表安装2梁段时1梁段的位置,C代表安装梁段②自由端的位置。故HB,HC分别为安装梁段①,②时的预拱度,即为安装高度,现欲求得旧梁段A2' B2'与新安装梁段B2'C的拼装时的角度。在A2'点作平行于AB的辅助线至P点,B2'Q为曲梁段①前端的切线交PA2'与点Q,形成的夹角为∠4,即为梁段①端面转角。容易看出α=∠2-∠1=∠2-∠8+∠3=∠2-∠5+∠6+∠3=∠2-∠5+∠4=∠2-∠7+∠4。其中∠2称为前端转角,∠7称为后端转角,∠4称为端面转角。∠2=(HC-HB'2)/L2。L2为梁段②长度。可看出该阶段的前端转角即为安装下一新梁段的后端转角。即∠2为安装梁段③时的后端转角。凤凰一桥梁段安装夹角α及制造线形计算过程如下表1。

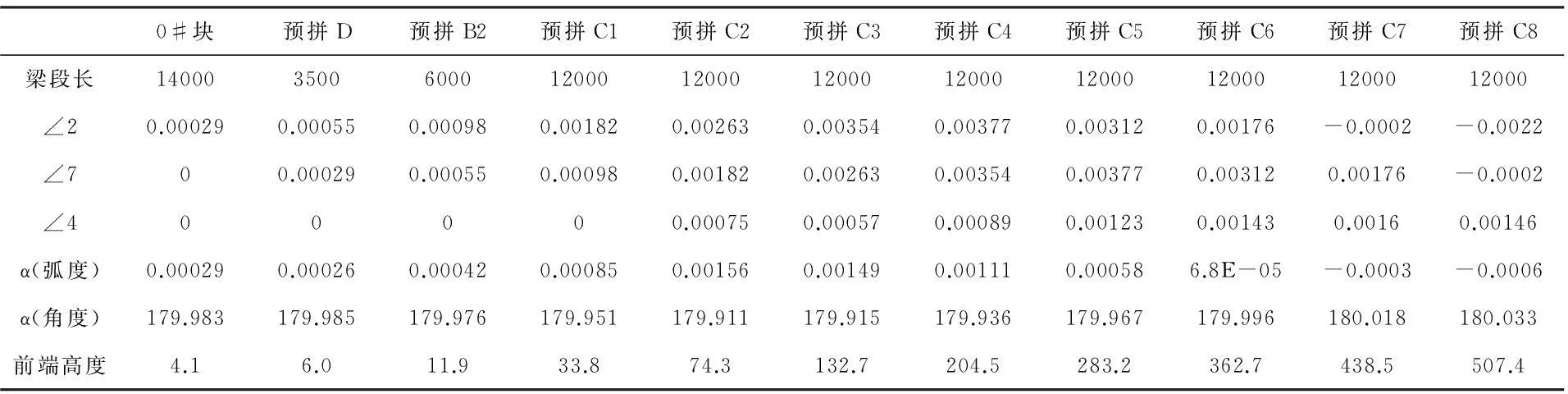
表1　安装新梁段与相邻旧梁段夹角α及制造线形计算

(注：α=前端转角-后端转角+端面转角,端面转角即图4中∠4,可直接从midas模型计算结果中提取。前端高度Hi+1=Hi+(Hi-Hi-1)Li+1/Li+αLi+1,Hi+1为预拼第i+1块梁前端高度,按照各梁段前端高度点连线而成的折线即为无应力制造线形。表中角度单位°,弧度单位为1,长度单位mm)

3.2切线初始位移法

切线初始位移法简称切线法, 是将新节点初始位移指定到沿着已安装梁段悬臂端切线上的。根据Midas计算位移的原理,用切线法计算制造线形时,应将各个悬臂拼装的梁段单元从第一块梁段安装开始就全部激活,但是不施加自重等任何荷载，悬臂端部自由，边跨支架施工梁段及支座暂不生成，,随后再在某梁段实际安装时再将该梁段所涉及的荷载如自重，拉索力等施加上去。这样未安装的梁段则随着已施工梁段自由摆动(产生的都是刚体位移)。在切线法模型中,必须将梁单元材料容重设置为0,梁段自重由等效的外荷载代替,否则在梁单元激活的同时就已经承受了自重荷载,就无法达到我们的初衷-所有悬臂梁段一开始生成就是无应力的。这样计算出来的制造线形必然是错误的,必须严格按照既定的施工过程加载才能得出正确的制造线形，因为斜拉桥是多次超静定结构,结构内力和位移与荷载加载过程是一一对应的[5]。

切线法模型最后一个施工阶段各梁端前端节点的位移加上0.5*活载位移后连线即为制造线形。计算方法十分简洁直观。

表2　切线法计算结果

由上表可见,切线位移法与零位移法是一致的，计算出的制造线形应相同.两者有微小的差别可能是因为软件计算误差或者模型稍有的不同造成。

4应注意的问题

安装线形与制造线形是不同的, 安装线形又称为是指主梁在拼装过程中各新安装梁段自由端连接成的线形,即各梁段前端节点安装坐标的连线。安装线形不可作为制造线形,制造线形是无应力的线形,而架设过程中已成梁段已经受力发生变形,新梁段则几乎处于无应力状态；新梁段如果要按安装线形计算的角度去拼接，则前端会无法达到安装标高，最终偏离设计线形。因此安装线形作为制造线形在理论上也是不可行的[6]。

零位移法只能用于线性问题,用于非线性分析时存在畸变问题[7]。用切线初始位移法求解制造线形的时候必须注意与主梁相交的支座的处理,如辅助墩，有学者认为可以用等效反力代替[8],笔者认为如此处理有些繁琐，因为每个施工阶段辅助墩反力是变化的，要按其反力增量一次次的施加。其实如果在主梁实际与辅助墩相连的时候再将支座激活，其作用与等效反力是一样的，只是要特别注意如果不是拉力支座，支座出现负反力时应将其钝化。切线法可十分快速简便的得到计算制造线形,但却无法得到安装新梁段时的自由端安装坐标，即无法得到安装线形。而零位移法在计算过程中已包含安装线形。

一般桥梁均设置了纵坡,上文叙述两种方法计算时未予考虑,纵坡对制造线形影响不可忽略,甚至会使其反向。计入纵坡影响后的凤凰一桥制造线形如图6。