复杂网络全局拓扑相似度计算方法实证研究
2015-12-25胡燕祝权桁艾新波
胡燕祝++权桁++艾新波

摘要:相似度研究对于复杂网络的链路预测、演化机制以及社团检测等相关热门研究领域都具有重要的作用,本文从网络相似度及演化的角度出发,基于提取复杂网络全局拓扑特性,定义了一种新的复杂网络相似度计算方法,仿真结果表明,该相似度计算方法可以准确表征不同复杂网络的相似程度,通过将该方法应用于技术交易中进行实证分析,发现可以将技术交易分为三个不同的阶段,每一阶段内的复杂网络之间相似度明显高于该阶段外的复杂网络,证实了本文提出的相似度计算方法具有可行性与有效性。
关键词:复杂网络;相似度;全局拓扑特性;技术交易
中图分类号:TP319
文献标识码:A
DOI:10.3969/j.issn.1003-6970.2015.09.004
0 引言
复杂网络即具有白组织、白相似、吸引子、小世界、无标度中部分或全部性质的网络。对于复杂网络相似度研究的意义主要在于以相似度研究为基础来准确进行链路预测、有效检测社团网络以及探索复杂网络的演化机制等,例如Chao S.根据节点之间的相似性来判断两节点之间建立连接的可能性,即链路的演化预测;社交网络中也经常使用复杂网络技术进行用户挖掘;基于相似度的算法也经常用来进行社团检测,它基于全局或者局部网络特性来计算节点之间的相似度,结合一般聚类算法来进行社团划分,此外,Girvan和Newman也曾基于边移除的算法来实现社团检测,即GN算法;赵伟艇等也基于节点相似度特性和三角结构提出了一种复杂网络演化算法,以上都是当前对于复杂网络研究比较热门的领域。
目前,关于复杂网络相似度的研究主要是自身局部相似度以及复杂网络节点间的相似度研究,例如王林等通过提出一种基于局部相似度的K-means谱聚类算法,计算节点间相似度,达到对网络中社团进行检测的目的;李佳佳提出一种自相似复杂网络,其主要根据通过提出一种基于节点的共有邻居数目的指数来描述节点相似度的局部相似度。
以上文献所研究的相似度均为节点或局部的相似度,并没有对全局拓扑特性的相似度进行研究,所以,为探索复杂网络整体拓扑结构的相似度算法,本文主要基于提取全局的复杂网络拓扑结构特征来计算不同复杂网络的相似度并进行研究与实证。
本文主要研究方法为算法研究结合实证分析验证,通过对技术交易复杂网络全局拓扑特征的选取以及计算提取,构建表征复杂网络全局特征的特征向量,对比常见的距离计算方法,得出对本文相似度计算最为有效的距离度量方法,最后通过对网络进行层次聚类可视化地展示相似度计算效果,并根据数据的实际意义来分析不同类别的复杂网络具有何种特征以及网络的演化发展趋势。
本文接下来安排如下,第1节是数据的描述;第2节为复杂技术交易网络拓扑特征的选取以及相似度方法的阐述;第3节是算法的仿真分析;第4节是相似度算法的实证研究及结果论证;最后第5节为本文工作的总结与展望。
1 数据描述及研究背景
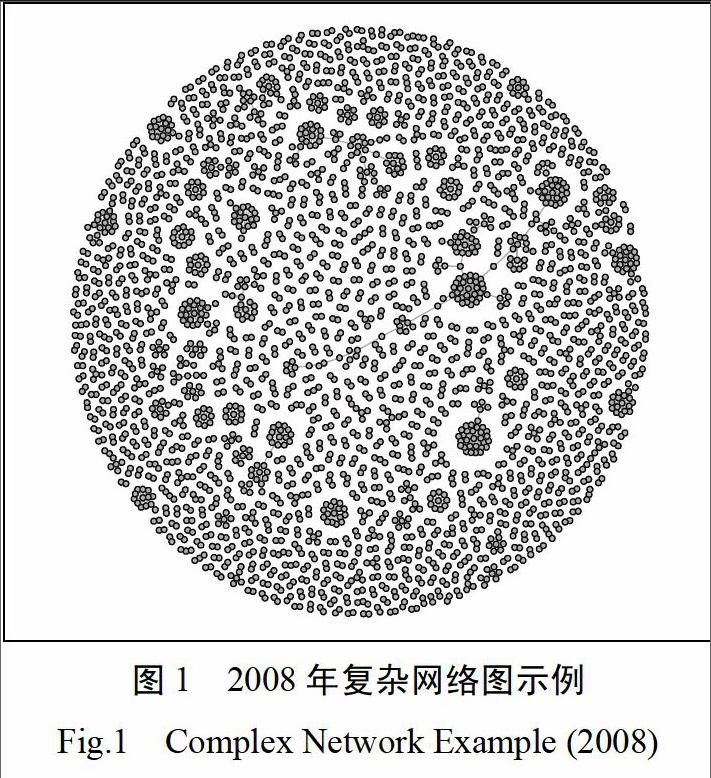
本文实证采用的数据为技术交易数据,技术交易即技术从卖方到买方的流通过程,由于这一过程涉及的企业数量巨大,企业之间的交易情况复杂,所以适合于用复杂网络来进行表征,技术交易可相当于复杂网络中两节点之间的连接行为。本文使用统计分析工具R语言中的igraph包对2006年到2014年共9年的技术交易数据进行网络构建,数据的主要字段包括:项目名称和领域,合同时间,买卖双方信息等字段,本文利用卖方名称、买方名称以及合同时间来进行技术交易复杂网络的构建,得到的网络模型(以2008年复杂技术交易网络为例)如图1所示。其中复杂网络的节点代表技术交易主体,包括技术卖方、技术买方以及技术中介等;复杂网络节点之间的连线代表着买方和卖方之间的交易。技术交易网络的节点和边描述了技术交易活动最主要的部分,除了边和点之外,复杂技术交易网络的某些拓扑特性也可以反映实际技术交易行为的特点。
2 网络相似度计算方法
本文所使用的网络相似度计算方法如下:首先对复杂网络的全局拓扑特征进行提取,所选特征需可以表征复杂网络的全局特性;然后根据拓扑特征建立复杂网络的特征向量,通过选取合适的距离计算方式计算特征向量之间的距离,即可映射为复杂网络之间的相似度大小。
2.1 拓扑特征的提取
在如上一节所描述构建复杂技术交易网络后,需要对网络的全局拓扑特征进行提取,本文结合技术交易的实际行为特点主要提取了七种拓扑特性指标,如表1所示。
对每年的技术交易复杂网络提取以上七种拓扑特征后,建立由这七种特征取值组成的网络特征向量,进而建立不同年份复杂技术交易网络的特征矩阵。
2.2 距离计算方法的选取
本文所用相似度计算方法的另一个重点是不同复杂网络的特征向量的距离计算方法,计算距离的方式有多种,主要有欧氏距离、曼哈顿距离以及余弦距离等,本文通过计算方式及实际意义对比来进行选取。
2.3 可视化展示
通过对不同复杂网络的特征向量进行距离计算,得到不同年份复杂技术交易网络的距离矩阵,根据该矩阵进行自底向上的层次聚类方法得到复杂网络的相似度结果,类标号一致的复杂网络相似度高,若同一类的复杂网络确有相似的生成模式,那么证明本文的相似度计算方法是可行的。
3 算法仿真分析
为了证实本文对于复杂网络相似度研究的可行性,笔者采用对无标度网络生成模型进行仿真的方式来验证。无标度网络是一种度分布呈幂律分布的复杂网络,其明显特征即具有择优连接特性,即度大的节点被连接的概率较大。因现实中大部分网络都具有或多或少的无标度特性,所以本文选取无标度网络进行仿真实验。
仿真所使用的工具仍为R语言的igraph包,其中barabasi.game函数可用来生成无标度网络,对无标度网络生成控制采用两种属性参数:每时步网络新增连接数m和无标度网络择优连接的强度power,其中power的数值越大,表示网络的择优连接特性越明显。
所选参数具体数值如表3所示:
由表3可得12种m和power的组合,即仿真生成12个无标度网络,序号为l到12。根据事先定制的无标度网络生成模式,我们预期根据本文的相似度计算方法可以将这12个无标度网络分成4类:{l,2,3},{4,5,6},{7,8,9},{10,11,12},即生成模式相近的网络之间相似度较大。仿真结果如图2所示:
由图2可以发现,使用本文所使用的相似度计算方法,可以将具有相似生成模式的无标度网络聚到同一类中,证明了根据本文提取的复杂网络拓扑指标建立特征向量可以比较准确的表征复杂网络的全局特征,此方法具有可行性。下面采用该相似度研究方法对实际的技术交易复杂网络进行实证分析。
4 相似度算法实证分析
上一章算法仿真分析是以无标度网络为实验网络的,为了证明算法可以应用于复杂技术交易网络,我们先证明复杂技术交易网络具有无标度特性即可。而这一点可以通过网络的度分布来反映,复杂技术交易网络的度分布如图3所示,可以看出,左图为度的长尾分布,右图对横纵轴取对数结果近似一条直线,可知复杂技术交易网络的度分布呈现幂律特性,证明其具有无标度特性。
由于技术交易的合同通常为若干年,所以数据预处理时先将每条交易记录的合同年份跨度标出,然后遍历数据,选取合同年份跨度中包含当前时间的交易加入到该天的复杂技术交易网络中,这样可以很好的保持网络中节点和边的生存周期。实证分析所取数据以月份为单位构建复杂网络,对每月内的特征数据进行取平均值的操作。
复杂网络拓扑特性的提取使用的是R语言igraph中的封装好的函数,包括度计算(degree)、平均路径长度(average.path.length)、直径(get.diameter)、聚集系数(transitivity)以及介数(betweenness)。将得到的特征向量组成特征矩阵,对特征矩阵每一种特征分别进行归一化处理,之后计算向量之间的距离,得到不同年份复杂技术交易网络的距离矩阵,根据距离矩阵使用hclust函数进行层次聚类,类与类之间的距离使用“complete”距离参数。
由于聚类结果中月份较多,使用层次聚类图展示不方便观察,所以笔者将每个复杂网络所属的类标号及日期绘制成图如下所示:
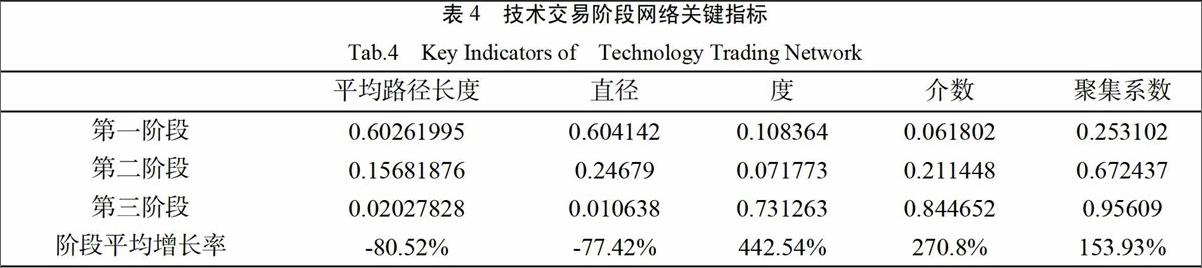
由图4圆点代表第一类网络,三角表示第二类网络,方块代表第三类网络,可见,根据本文的相似度计算方法将不同年份的复杂技术交易网络按照拓扑结构相似度聚类到一起,总体来看效果较好,没有出现异常的单独月份,从拓扑结构来看,月份相近的网络确实在结构上相似度较高,使用本文的相似度计算方法将技术交易的发展大致分为了三个阶段,在不同阶段交界处存在着模糊阶段可忽略:其中2006到2008为第一阶段,2009年到2013年为第二阶段,之后为第三阶段。每个阶段的关键指标归一化平均值计算结果如下表所示:
由表中数据可见,复杂技术交易网络发展的三个阶段过程中,平均路径长度以及直径都在减小,而度、介数和聚集系数这三个指标都在增加,很清晰地说明了技术交易成果转化效率逐步提高,技术交易整体具有技术集中化、合作多元化的趋势。
5 结论
本文提出了一种基于复杂网络全局拓扑特性的型相似度计算方法,即提取复杂网络的全局拓扑特征建立复杂网络的特征向量,通过计算特征向量的距离来对复杂网络进行聚类。方法的验证是通过使用无标度网络进行仿真分析以及基于技术交易数据的实证分析,验证结果对该相似度计算方法给予了充分的证明,该方法在计算复杂网络之间的相似度中具有可行性与可信性,根据该相似度计算方法将技术交易大致分为了三个阶段,阐述了技术交易市场的发展趋势,主要工作包含以下4点:
1、对技术交易数据进行预处理
2、构建复杂技术交易网络并提取拓扑特征
3、对复杂网络特征向量进行距离计算
4、对聚类结果进行解释并探索原因
本文使用的相似度计算方法在于拓扑特征为基于全局网络提取的,构建的特征向量可以比较全面得代表复杂网络的整体特征,对复杂网络的相似程度计算较为准确。但是该方法扔存在可优化的空间,比如拓扑特征数量比较少,可以寻找更多具有代表性的拓扑特征。另外,拓扑特征之间可能存在着一定的线性关系,对多维度的拓扑特征如何进行降维(如主成分分析等)也是笔者下一步准备研究的内容之一。