基于改进BP的神经网络模型参考自适应控制
2015-12-25张敏徐启华
张敏 徐启华

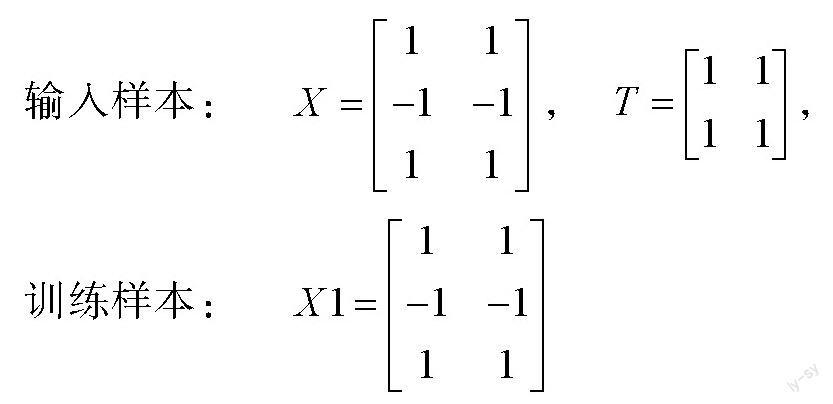
摘要:由于传统BP算法存在收敛速度慢,容易陷入局部极小值等弊端,目前的BP优化算法又使得控制过程变得复杂,继而基于BP神经网络的模型参考自适应控制过程也存在实时性差,收敛性慢,精度不高等不足。现针对改进的BP算法和非线性系统的可逆性,分析设计了一种基于激励函数自寻优的BP网络模型参考自适应控制,并通过Matlab仿真结果表明,在满足控制精度的情况下控制系统中的辨识器和控制器效果都很理想。因此,对工程应用有很大的实际参考利用价值。
关键词:BP算法;神经网络;模型参考自适应控制;激励函数;Matlab仿真
中图分类号:TP183
文献标识码:A
DOI:10.3969/j.issn.1003-6970.2015.07.024
0 引言
在现代实际工业生产中,被控对象存在各种不确定性和时变性,因而使得工业控制过程变得繁琐复杂,针对线性时变系统或非线性系统的控制,人们不断的研究其解决方法,Nare ndra等人提出了神经网络控制和模型参考自适应控制相结合的神经网络模型参考自适应控制(Neural Network Model Reference AdaptiveControlˉˉˉNNMRAC)方法。近来神经网络的研究已成为智能控制研究的热点,因其自身具有自学习的特点,可以有效地解决不确定和复杂的非线性控制系统控制问题。因此将神经网络与模型参考自适应控制相结合,组成基于神经网络的模型参考自适应控制系统,进而使其在复杂非线性过程控制中具有不可替代的优势。目前神经网络模型参考自适应控制系统中应用最广泛的神经网络是BP神经网络。
BP神经网络(Back Propagation Network)是一种多层前向型神经网络也被称为反向传播网络,在BP网络中信号是前向传播的,而误差是反向传播。一般三层BP网络结构就可以使其对有限个不连续点的函数进行逼近,也可以逼近任意非线性映射关系。然而,传统BP神经网络算法存在很多缺点,各种优化改进的BP算法也层出不穷。就目前的BP优化算法,常常忽略算法本身存在的自适应、自学习等特点,改进算法如蚁群算法和粒子群算法大都是直接对BP神经网络中的参数进行训练。文中采用基于激励函数自寻优的方法改进BP神经网络模型参考自适应系统的控制方法,改进后的BP神经网络模型参考自适应控制方法收敛速度快、精度高,系统控制过程中被控对象的输出能够很好地跟随参考模型的输出,具有很好的控制效果,在实际工程中也可以得到很好的验证和应用。
1 BP神经网络结构及其算法改进
BP神经网络已经被证明具有很强的学习能力,能够逼近任意连续有界的非线性函数。一般的BP神经网络包括输入层、隐含层、输出层,其中隐含层可以有多个。其中隐含层和输出层的激励函数通常直接采用Sigmoid函数,其函数表达式为:
上式中β称为Sigmoid函数的斜率参数,不同的β取值,引起曲线的弯曲程度不同,β越大,f(x)图形越陡峭。当斜率参数β接近无穷大时,Sigmoid函数将转化成简单的阶跃函数。但与阶跃函数不同,Sigmoid函数对应于0~1之间的一个连续取值区域,但阶跃函数只对应0和1两个取值。
一般的三层前馈神经网络拓扑结构如图1所示。
输入向量为Xi=(Xl,X2…,Xn)T,i=1,2,…,n,n表示输入神经元的个数,隐含层的输出向量为yj= (Y1,y2,…,ym),j=l,2,…,m,输出层的输出向量为Ok= (Ol,O2….,ol),k=l,2,…,l。每层之间的权值用w表示,Wij为隐含层和输入层之间的权值,Wjk为输出层和隐含层之间的权值。
这里对上述BP算法的改进,也就是通过改进激励函数f(x),进而优化神经网络,最终使得基于神经网络的模型参考自适应控制在不增加复杂性及确保精度的情况下,系统性能进一步得到提高改善。由于BP神经网络产生局部极小值的一个重要原因就是误差函数是一个以Sigmoid函数为自变量的非线性函数,而Sigmoid函数存在饱和区,所以改进和优化激励函数对于BP算法的应用是至关重要的。通过实验发现,在函数表达式中增加一个控制参数η,可以控制激励函数的压缩程度。改进的激励函数形式如下:
上式描述的f(x)的定义域为(-∞,+∞),值域为(0,1),函数也是单调的,满足激励函数的条件。
以往出现的改进BP算法学习过程中,η和β的赋值都是经验值,本文使得η是一个可以自适应的参数,就是通过判断网络不断学习过后的权值能否减小网络误差来自动的调整η的值,其调整方法为:
其中,al,E为网络误差,f指迭代次数。在误差信号反向传播时,自适应参数η是随着误差信号不断进行修正的。
此算法可以提高BP网络的收敛速度,同时也避免了陷入局部极小值。文中使其结合模型模型参考自适应控制明显提高了系统的整体控制效果,进一步验证了算法改进的实用性,与传统BP算法相比,改进后的算法在实际运用中更具有意义。
2 神经网络模型参考自适应控制系统结构
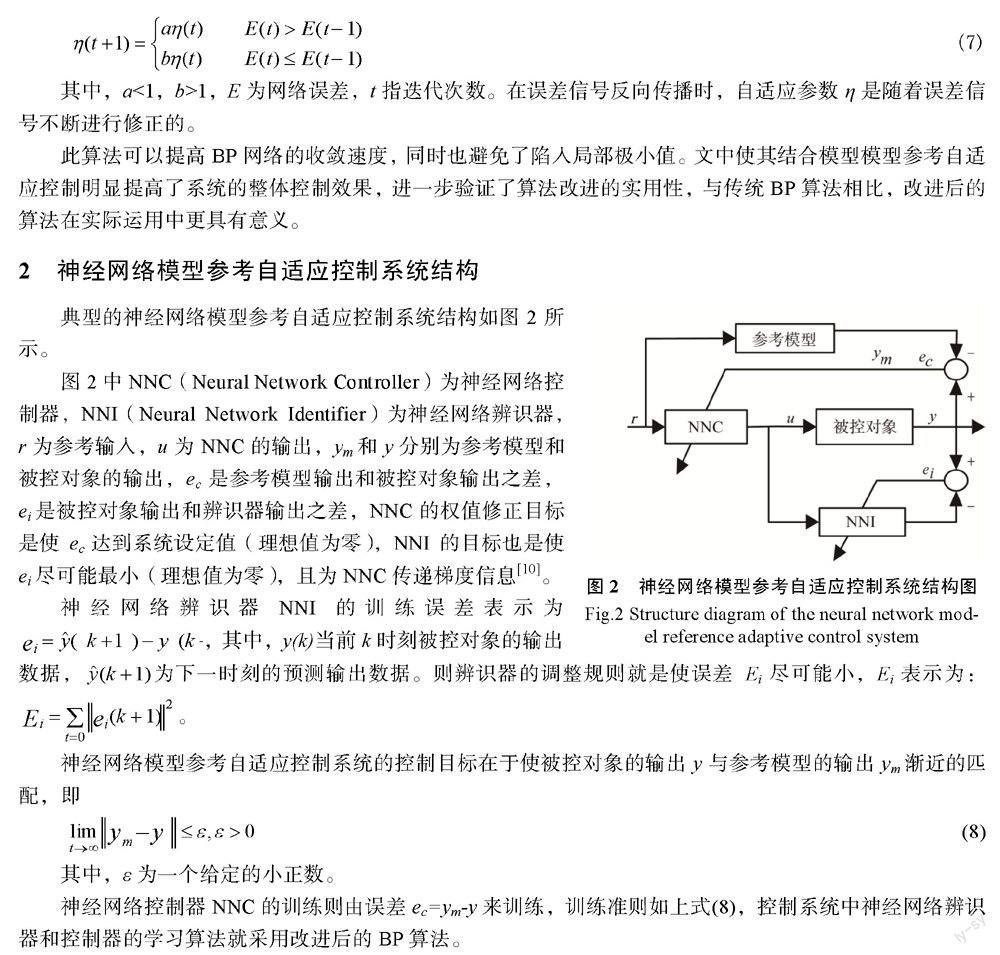
典型的神经网络模型参考自适应控制系统结构如图2所示。
图2中NNC( Neural Network Controller)为神经网络控制器,NNI( Neural Network Identifier)为神经网络辨识器,r为参考输入,u为NNC的输出,Ym和y分别为参考模型和被控对象的输出,ec是参考模型输出和被控对象输出之差,ei是被控对象输出和辨识器输出之差,NNC的权值修正目标是使ec达到系统设定值(理想值为零),NNI的目标也是使ei尽可能最小(理想值为零),且为NNC传递梯度信息。
神经网络辨识器NNI的训练误差表示为 ,其中,y(k)当前k时刻被控对象的输出数据, 为下一时刻的预测输出数据。则辨识器的调整规则就是使误差Ei尽可能小,Ei表示为:
神经网络模型参考自适应控制系统的控制目标在于使被控对象的输出y与参考模型的输出Ym渐近的匹配,即
其中,s为一个给定的小正数。
神经网络控制器NNC的训练则由误差ec=ym-y来训练,训练准则如上式(8),控制系统中神经网络辨识器和控制器的学习算法就采用改进后的BP算法。
在神经网络模型参考自适应控制系统的控制策略设计中,改进的BP算法能够在满足系统控制规律符合要求的情况下,使得神经网络模型参考自适应控制效果更好。虽然改进的BP算法是激励函数自寻优的自适应方法,不能够使神经网络辨识器NNI进行离线训练,但是快速的BP算法仍然可以使网络具有很好的实时性。首先在线训练辨识器,待参数训练好以后,再进行控制器NNC的训练,最终可以保证被控对象的输出y很好的跟踪参考模型的输出Y。
3 仿真实例研究
3.1 改进的BP算法验证
本文采用BP神经网络进行预测控制来验证改进算法的有效性。利用简单的一组样本训练集和样本目标集进行神经网络的训练,再给定一组输入样本数据,观测输出层输出数据和误差。分析样本数据设计BP神经网络结构为3个输入、2个输出、隐含层的神经元数目为8。网络学习次数为100次,目标误差设置为0.001。
使用MATLAB软件进行网络训练,传统BP算法的网络训练过程收敛情况如图3所示,经过56步循环达到了网络误差要求的精度。改进的BP算法网络收敛情况如图4所示,仅需要10步就达到了误差精度要求,其中a和b取值分别为0.9和1.5。输出误差和网络实际输出数据在表1中展示,直观的看出,改进后的BP网络可以得到更有效的输出。
根据得到的误差收敛曲线比较看出,改进后的BP算法所用训练步数少即需要的训练时间少,说明收敛速度明显加快。
测试输出结果如表1所示。
从表中可以直观清晰看出改进后的BP算法实际输出误差明显减小,提高了算法精度。
3.2 改进的神经网络模型参考自适应控制仿真实例
结合参考文献中提到的污水处理的例子进行改进算法的验证。污水处理系统结构图如图5所示,
在污水处理系统控制结果是否达标,主要是通过需氧量(OD)、溶解氧(DO)等几个重要参数来衡量。本例中为了提高污水处理效果,系统控制目标设置为使误差ec控制在±0.05mg/L以内,污水处理控制系统中采
用离散的参考模型:
ym(k)= 0.375 ym(k-1)+0.623r(k)
其中,控制输入r(k)=2为系统给定的阶跃信号。
污水处理系统的实验仿真中,BP网络辨识器设定4个输入变量和1个输出变量,隐含层包含10个隐节点,对于BP网络控制器取3个输入层节点,隐含层的节点数为6。根据BP神经网络控制器和辨识器的改进算法,采用MATLAB进行仿真,取采样周期ts=0.OOls,这里a取0.8,6取1.5,仿真结果如图6所示。
在图6 (a)中第一条线为控制输入r,中间的第二条曲线代表参考模型的输出Ym,最下边的曲线代表污水被控对象的输出y,图6 (b)中的曲线代表误差ec(系统实际输出与参考模型输出之差)的变化。从图中可以分析看出,改进后模型参考自适应控制方法在该控制系统中的控制效果很好,氧的溶解浓度(DO)保持在2mg/L左右,参考输出和实际输出最终相吻合,误差ec控制在±0.05mg/L以内,因此仿真结果满足控制系统的控制要求。
4 结语
本文采用改进后的BP神经网络作为模型参考自适应控制中的辨识器和控制器,由仿真结果表明,BP算法在简单有效的改进后,提高了BP网络的收敛速度,进而在模型参考自适应控制系统中达到良好的实时性,同时满足了控制系统在线训练的要求。虽然本文提到的BP改进算法对太复杂的智能控制系统影响不是太大,但在实际工程应用中,只要充分结合运用不同的改进BP算法的方法就可以达到比以往更理想的效果。
