基于概率熵判据的大坝位移预警概型比较

2015-12-25张炯，叶琦

江西水利科技 2015年6期

张炯，叶琦

（江西省赣抚平原水利工程管理局，江西南昌 330096）

0 引言

大坝效应量安全监测资料众多，其中位移监测直观、可靠，通过拟定大坝位移预警指标来实现大坝安全监控具有重要意义[1]。大坝产生变形的因素既包括如水压、温度及时效等已知因素，又包含众多未知及不确定性因素。借助先进的数理统计工具，利用大坝位移原始监测资料，针对大坝经历不利荷载时位移监测序列，采用小概率估计方法建立位移预警指标估计模型，是实现大坝位移预警的重要手段[2]。大坝服役性态一般可分为3个阶段：运行初期、正常运行期和老化耗损期，其失效期分别对应：早期失效期、正常运行偶然失效期和耗损失效期[3]。各失效期失效率η(t)与服役时间t构成浴盆曲线如图1。

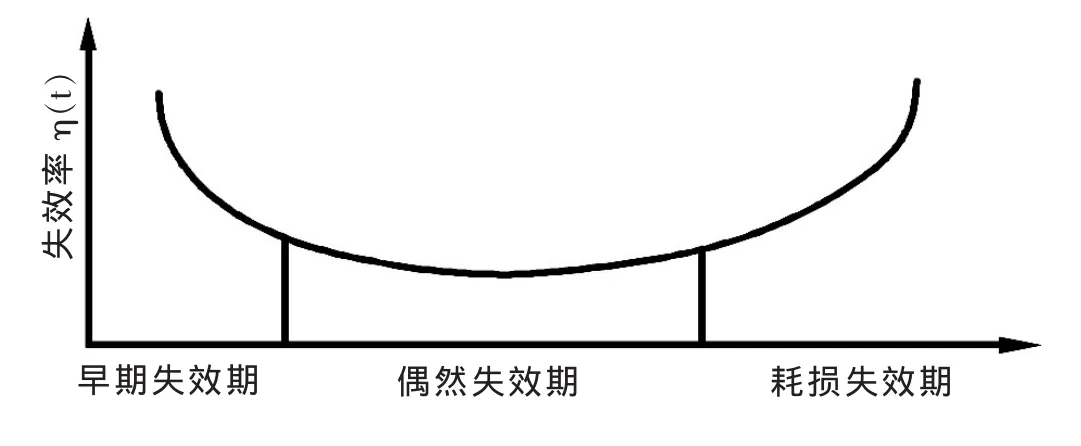
图1 工程失效率浴盆曲线

系统可靠度分析中，因Weibull分布、Gamma分布和Log-normal分布能够很好或较好的适应浴盆曲线的3个失效期，故成为常用的小概率分析方法[4，5]。但分布是否能客观描述系统性态以及分布优劣评价判据研究较少。文献[6]研究了3种概率分布对大坝服役性态的刻画，但其通过经验分布与理论分布的差异性作为判据来度量服役性态描述效果有失客观性。水工混凝土结构具有很明显的非线性自组织机制和多尺度耦合效应，其宏观效应量是内部不同尺度物理量协同作用的外在表现[7]。熵具有能量概念，可借助熵来完成不同尺度和层次的统一分析[8]。为能客观描述大坝服役性态，本文基于文献[6]研究思路，阐述了基于熵判据的大坝位移预警概型比较工作，并利用某坝典型坝段坝顶径向位移实测资料，结合所拟定的大坝失事概率[7]，完成了位移预警指标的估计，以期为其他工程位移预警提供借鉴。

1 建立大坝位移预警估计模型

1.1 大坝位移预警概率分布模型

1.1.1 Weibull分布模型及其参数估计

以大坝位移监测年极值序列作为大坝经历不利荷载时的位移监测序列{xi}，利用Weibull分布对其进行拟合，得到Weibull分布概率密度函数(PDF)和分布函数(CDF)分别为：

式中：γ为位置参数，用来描述分布位置，γ=0时为二参数Weibull分布；η为尺度参数，对分布幅度进行刻画；β为形状参数，为分布最重要参数，描述分布形状，β取不同值时可使分布拟合图1浴盆曲线不同阶段，故Weibull分布是进行可靠性分析的常用手段，可以很好的拟合各类可靠性数据[9]。通过文献方法[4，6，10]对比，亦可采用文献[4]中所述方法实现Weibull参数估计。

1.1.2 Gamma分布及其参数估计

同样，利用Gamma分布拟合序列{xi}后的PDF和CDF分别为：

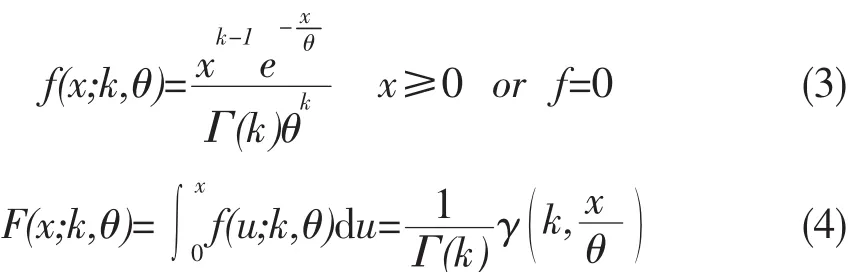
式中：k为形状参数；θ为尺度参数；Γ为Gamma函数；u为中间变量。

Gamma分布参数估计方法主要有极大似然法，期望极大化算法等[11，12]。本文采用通用的极大似然估计进行参数估计。

1.1.3 Log-normal分布及其参数估计

Log-normal分布拟合序列｛xi｝后的PDF和CDF分别为：

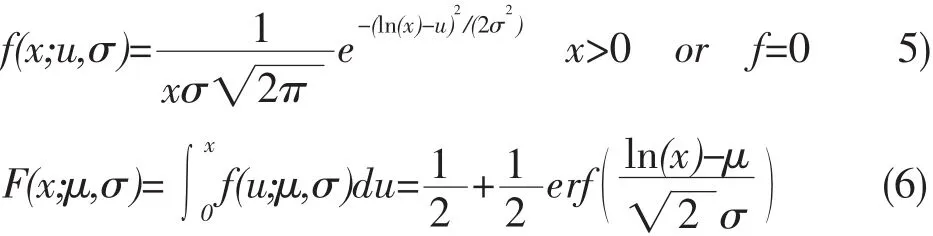
式中：μ为位置参数；σ为尺度参数；u为中间变量。

{xi}服从Log-normal分布的前提条件是{ln(xi)}服从Normal分布，本文通过计算{ln(xi)}的峰度和偏度系数，构造JB统计量进行检验。并借鉴Normal分布参数估计方法利用极大似然估计进行参数估计。

已知分布参数的情况下，结合大坝失事概率，由F-1(x)分布函数反函数可求得位移预警估计值。

1.2 位移预警概率分布模型合理性检验

利用概率分布对位移监测序列进行拟合，需对其拟合质量进行诊断。本文借助K-S检验法对概率分布拟合效果进行检验[13]。其先考虑假设：

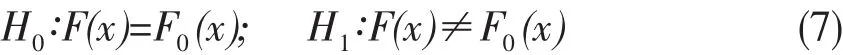
其中F0(x)为已知分布函数。利用经验分布函数Fn(x)与已知分布函数F0(x)之间的偏差构造统计量。记：

K-S检验的方法是通过样本xi计算Dn，若Dn＜D0，则接受原假设；否则，拒绝原假设。偏差统计量临界值D0(取显著性水平α=0.05)值通过查表[14]可得。

1.3 概率分布最大熵原理

最大熵原理是一种选择随机变量统计特性最符合客观情况的准则。大坝位移量源于设备实际监测，带有可靠的大坝服役性态信息，熵越大则表明大坝位移量越随机，对大坝服役性态描述越客观。它的定义式由香农提出：

对离散随机变量，熵定义为：

对连续随机变量，熵定义为：

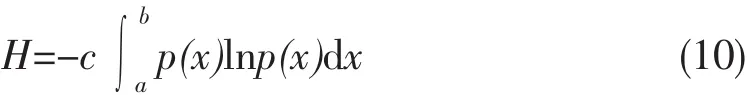
式中：c为常数，常取 1；b，a为变量上下限；p(x)为概率密度函数。

根据熵的定义式（9）与（10）以及各分布的概率密度函数，推求得到：

Weibull分布熵计算公式：

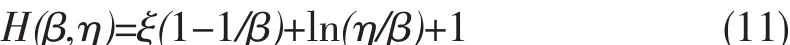
式中：ξ为欧拉常数，取 0.577 215 6；η为该分布尺度参数；β为该分布形状参数。

Gamma分布熵计算公式：

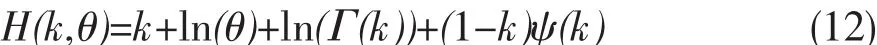
式中：ψ(k)=E(ln(X))-ln(θ)，k为该分布形状参数；θ为该分布尺度参数。

Log-normal分布熵计算公式：

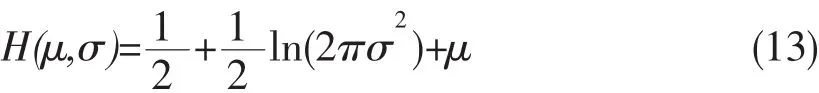
式中：μ为该分布位置参数；σ为该分布尺度参数。

1.4 大坝位移预警指标估计过程

为了直观了解位移预警指标估计过程，其基本流程见图2。

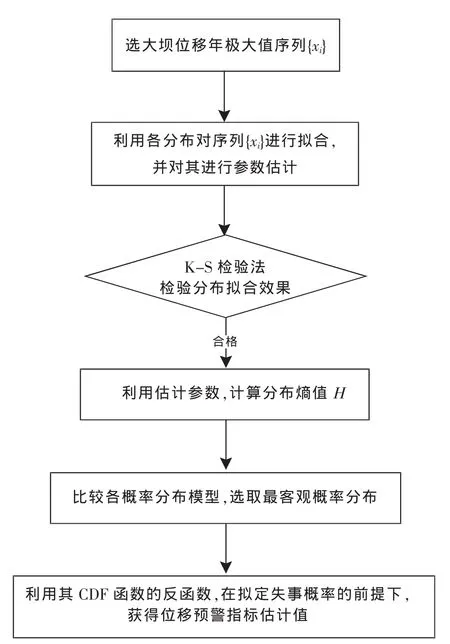
图2 大坝位移预警指标估计流程图

2 实例分析

某水利枢纽位于广西壮族自治区，地处珠江流域，以防洪发电为主，兼具航运效益。枢纽包括拦河坝、坝后发电厂房、开关站和垂直升船机，溢流坝以碾压混凝土坝为主。坝顶高程为233.00 m（黄海高程，下同），最大坝高为 110.00 m，坝顶全长 525.00 m，分 28 个坝段。设计水位 223.00 m，总库容为 26.12 亿 m3，为大(1)型水电站。本文依据该坝 3#，10#，18#，24#典型坝段在 1997～2006年间坝顶向下游径向位移年极值构成不利荷载效应量序列{xi}，建立概率分布模型。并依工程概况，拟定该坝失事概率为1%。各坝段年极值序列列于表1，模型相关参数估计见表2。

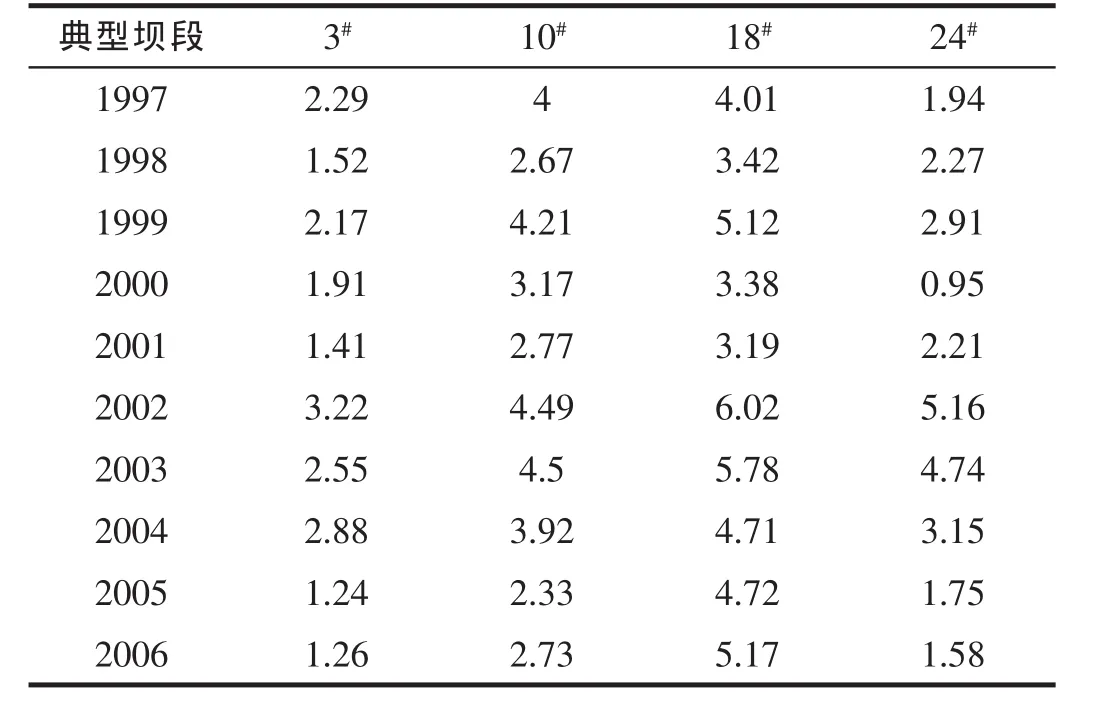
表1 典型坝段坝顶向下游位移年极值序列 mm

从表3可以看出：在置信度0.05情况下，各分布K-S检验值均小于临界值0.409，故均满足检验。

根据概率分布熵公式，即式（11）～（13），结合表 1概率分布参数估计，计算各分布熵，见表4。

从表4并结合最大熵原理可以得到：Weibull-3分

表2 概率分布参数估计

对所建概率分布模型进行K-S合理性检验，见表3。布可较客观描述 3#、10#、18#、24#坝段坝顶径向位移。

最后，假定大坝失事概率1%，利用概率分布函数进行大坝位移预警指标估计，便于对比，将其他分布估计结果一并列于表5。

结合表 4 与表 5，可以得到：3#、10#、18#、24#典型坝段坝顶径向位移预警估计值分别为4.24 mm、5.58 mm、7.08 mm、7.47 mm，其他分布模型存在欠估计或过估计现象。

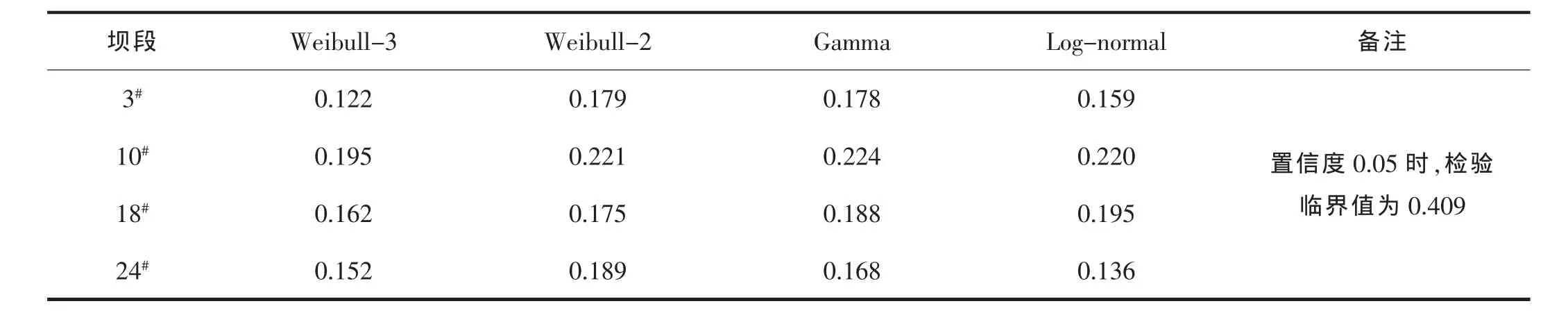
表3 K-S检验

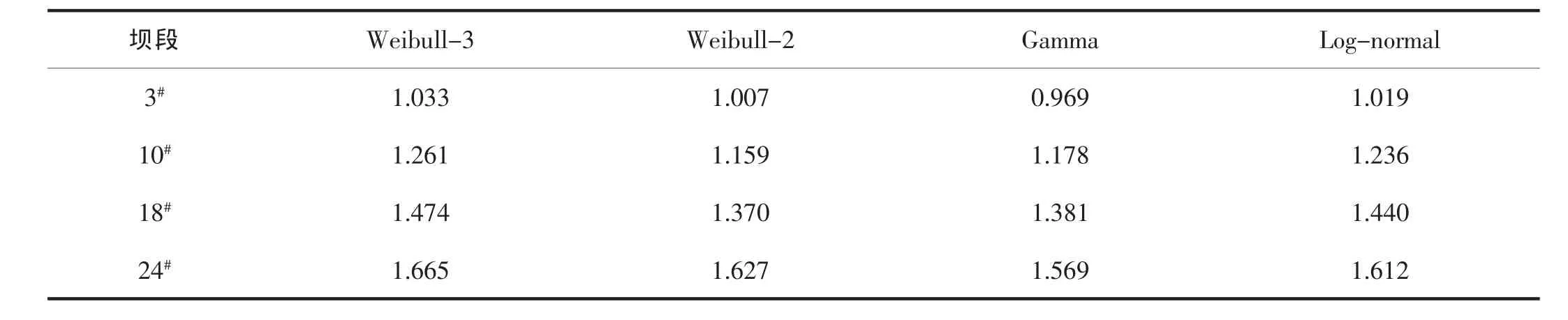
表4 概率分布熵计算

表5 预警值估计mm

3 结语

针对大坝服役性态自身特点，利用Weibull分布、Gamma分布、Log-normal分布对大坝典型坝段坝顶位移进行概率拟合分析，完成了概率分布模型建立、检验、对比及预警值估计工作。得到：对于 3#、10#、18#、24#典型坝段，依据最大熵原理，三参数Weibull分布模型能较可靠的实现位移预警估计，说明三参数Weibull分布能最客观描述典型坝段服役性态，是一种可靠的系统可靠度分析手段。

[1]何金平，程丽.大坝安全预警系统与应急预案研究基本思路[J].水电自动化与大坝监测，2006，30(1)：1-4.

[2]赵尚传，赵国藩，贡金鑫.在役混凝土结构最优剩余使用寿命预测[J].大连理工大学学报，2002，42(1)：83-88.

[3]虞鸿，李波，蒋裕丰.基于威布尔分布的大坝变形监控指标研究[J].水力发电，2009，35(6)：90-93.

[4]郭必柱，邓建.可靠性分析威布尔三参数估计方法比较分析[J].科学技术与工程，2010，10(25)：6117-6122.

[5]Eckhard Limpert，Werner A.Stahel，Markus Abbt.Log-normal Distributions across the Sciences：Keys and Clues[J].BioScience，2001，51(5)：341：352.

[6]王子敬.基于概率分布的大坝服役性态预警指标估计[J].水电能源科学，2015，33(10)：65-67.

[7]雷鹏，常晓林，肖峰，等.高混凝土坝空间变形预警指标研究[J].中国科学：技术科学，2011，41(7)：992-999.

[8]何国威，夏蒙棼，柯孚久，等.多尺度耦合现象：挑战和机遇[J].自然科学进展，2004，14(2)：121-124.

[9] 刘惟信.机械可靠性设计[M].北京：清华大学出版社，1996：74-80.

[10]张秀芝.Weibull分布参数估计方法及其应用 [J].气象学报，1996，54(1)：108-116.

[11]H.C.S.THOM.A Note on the Gamma Distribution[J].Monthly Weather Review，1958，86(4)：117-121.

[12]P.Dempster A，B.Rubin D.Maximum Likelihood From Incomplete Data Via The Em Algorithm[J].Journal of the Royal Statistical Society，1977，39(1)：1-38.