塔式起重机附墙后塔身受力分析

刘　金， 黄国健， 卢立东， 王新华， 张　桢， 陈　敏

(广州特种机电设备检测研究院， 广东 广州　510663)



塔式起重机附墙后塔身受力分析

刘金， 黄国健*， 卢立东， 王新华， 张桢， 陈敏

(广州特种机电设备检测研究院， 广东 广州510663)

摘要：为验证某塔式起重机(塔吊)附墙后塔身应力计算工程经验算法的准确性，对塔吊附墙后塔身的受力状况进行探讨，以提高附墙后塔身应力计算的准确性.以某台塔吊模型为例，首先利用经验算法对附墙后塔身的应力进行分析计算，然后对塔身进行理论受力分析，推导出塔身的应力状况，接着通过有限元分析得到更为准确的塔身应力值，最后，将通过这三种方法获取的应力值进行对比分析.对比分析结果表明：经验算法的结果与有限元分析的结果存在较大偏差，其中最大应力偏差达81.8 MPa；而理论受力分析的结果与有限元分析的结果较接近，最大应力偏差为8.4 MPa.由此表明该工程经验算法在某些场合下误差较大，需要进行修正，建议使用理论受力分析或有限元分析.

关键词：塔式起重机； 附墙； 塔身； 受力探讨

0引言

塔式起重机(塔吊)具有工作效率高、回转半径大、起升高度大、操作方便以及结构模块化便于安装、拆卸及运输等特点，鉴于塔吊的上述优点，它在建筑安装工程中得到了广泛地应用，并成为一种重要的施工机械[1].塔吊作为一种重要的施工机械，但也伴随着危险多发性，鉴于塔吊的重要性和危险性，广大专家学者对其受力状况进行了分析探讨.

LiuQing等对塔吊在工作状态下的应力进行了分析[2]；LanfengYu对塔吊的静态刚度进行了分析，并提出了静态刚度的控制方法[3]；刘毅对起重臂结构强度进行了分析计算，可为起重臂的设计提供参考[4]；HOUXiao-ting等通过对塔吊进行受力分析，进而对塔吊结构进行优化[5]；R.Mijailovi等对吊臂进行了优化设计的研究[6]；朱冰等对塔吊进行了动力学分析，分析了塔吊起吊和卸载时的动态响应[7]；王武奇分析了塔吊在地震影响下的响应，为提高塔吊的抗震性提供了参考[8].

YongqiangGu等[9]和ZhiSun等[10]对强烈风载荷作用下塔吊的响应进行了研究，可为提高塔吊的抗风性提供参考；赵威威等通过对塔吊进行疲劳载荷分析，提出了一种疲劳寿命分析方法[11]；王冬明在对塔吊进行动力学分析的基础上，对塔吊的动态监测技术进行了研究[12]；张晓霞等对柔性附着塔吊的塔身进行了有限元分析[13];曹晔等则对柔性附着塔吊结构性能进行了研究[14]；广州特种机电设备检测研究院在塔吊受力分析方面做了一些包括有限元建模与分析、模态分析、附墙杆件受力分析等的研究[15-17].

广大专家学者围绕塔吊受力状况进行了大量分析，但并未针对目前工程界广泛运用的一种塔吊附墙后塔身应力的经验算法(详见下文)进行分析、验证，而该经验算法因为适用场合较窄而时常受到塔吊检测人员、设计人员及使用人员等的质疑.本文将对该经验算法进行分析，并借助理论受力分析和有限元分析进行对比验证，以分析该经验算法的准确性.

1经验算法

在工程界，针对最高附墙以下塔身主弦杆的应力计算，通常会采用一种简化的经验算法，即认为最高附墙以下塔身任一横截面所受的弯矩约等于最高附墙处塔身横截面所受的弯矩，其所受的重力即为该截面以上所有部件的重力，详细内容如下.

以某台塔吊为例，如图1所示，该塔吊在最大幅度时额定起重量为3t，工作幅度2～35m，最大起重力矩为1 029kN·m，起升高度80m，整机高度为89m，主体结构材料为Q235B.对最大幅度下起吊额定载荷时最高附墙以下塔身的受力情况进行分析，文中三种算法均以该塔吊为分析对象.

图1　某塔吊示意图

塔身由标准节组成，附墙1以下有7个标准节，附墙2以下有13个标准节，附墙2以下的13个标准节及以上的1个标准节从下到上依次命名为标准节1、标准节2、…、标准节14，每个标准节高为3m，长和宽均为1.7m.图2为标准节示意图，标准节由4根主弦杆和若干竖杆及斜杆组成，本文重点分析主弦杆的受力情况，所以图中主要体现主弦杆.为了便于分析，约定图1中吊臂一侧为塔吊的前侧，平衡臂一侧为塔吊的后侧.

图2与图1的X、Y轴指示方向一致，坐标轴原点为标准节中心，约定图2中X轴正方向一侧为标准节前侧，Z轴正方向一侧为标准节右侧.由于塔吊结构的对称性，标准节的左右侧受力情况一致，所以只选取标准节的右侧两根主弦杆进行受力分析，并约定位于前侧的主弦杆为前主弦杆，位于后侧的主弦杆为后主弦杆.为了进行对比分析，对每段标准节的上半节的前主弦杆和后主弦杆的中点进行受力分析，即图2中的Ai点和Bi点，Ai点和Bi点所在的横截面记为i截面，文中i=1,2,…,14.

图2　标准节示意图

将图1中附墙2处J-J截面以上所有部件及载荷产生的相对塔身中心线的弯矩叠加，即可求得J-J截面受到的弯矩M0=877.645kN·m，约定使塔吊前倾的弯矩为正.将标准节i的i截面所受的弯矩记为Mi，则Mi=M0.

则标准节i的Ai点由于弯矩产生的应力为：

(1)

式中，L0=1.7m，为标准节宽度，S0=0.003 744m2，为主弦杆的截面积.

同理易求得标准节i的Bi点由于弯矩产生的应力为：σBiMi=-σAiMi=68.945MPa.

J-J截面所受到的等效重力G0为截面以上所有部件的重力及载荷，易求得G0=311.875kN.假设标准节的质量按高度方向均匀分配，则标准节i的i截面所受的重力为：

(2)

式中，Mb=740kg，为标准节的质量，g=9.8N/m2，为重力加速度.

则标准节i的Ai点和Bi点由于重力产生的应力为：

(3)

综上，可得到标准节i的Ai点和Bi点的总应力分别为：

σAi=σAiMi+σAiGi=

(0.484i-96.186) MPa

(4)

σBi=σBiMi+σBiGi=

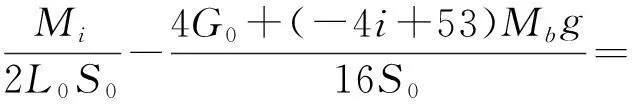
(0.484i+41.704) MPa

(5)

由公式(4)和(5)可求得标准节i的Ai点和Bi点的总应力，如表1所示.

表1　经验算法求得的各标准节应力汇总表

注：单位：MPa

2理论受力分析

图3为塔吊受力分析简图，将塔身简化为一连续梁结构，为了与经验算法进行对比分析，图3中塔吊受力情况与前文完全一致，附墙1和附墙2产生的支反力分别为R1和R2.

图3　塔吊受力分析简图

塔吊力学模型为一个二次超静定问题，利用结构力学中的力法易求得R1=-76.361kN,R2=60.888kN.

综上，易得到塔身沿高度方向的弯矩方程为：

(6)

由公式(6)可得到塔吊的弯矩图，如图4所示.

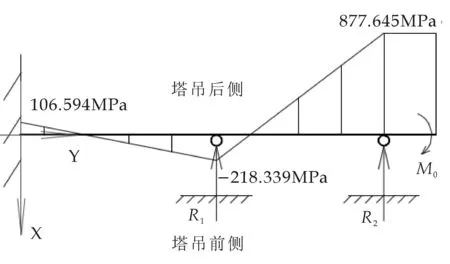
图4　塔吊弯矩图

标准节i的i截面的Y坐标yi=3i-0.75，则i截面受到的弯矩为：

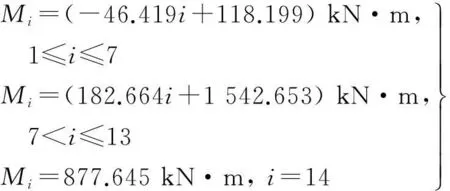
(7)

由式(7)可得标准节i的Ai点由于弯矩产生的应力为：

(8)

由式(8)易得Bi点由于弯矩产生的应力为：σBiMi=-σAiMi.

标准节i的Ai点和Bi由于重力产生的应力与第二节的结果完全一致，不再赘述.

综上，可得到标准节i的Ai点和Bi点的总应力分别为：

σAi=σAiMi+σAiGi=

(9)

σBi=σBiMi+σBiGi=

(10)

由公式(9)和(10)可求得标准节i的Ai点和Bi点的总应力，如表2所示.

表2　理论受力分析求得的各标准节应力汇总表

注：单位：MPa

3有限元分析

图5　塔吊有限元模型

为了进一步分析经验算法的准确性，对塔吊进行有限元分析，图5为塔吊有限元模型.在建立有限元模型时，进行了合理简化，例如，在实际塔吊中标准节之间通过螺栓连接，而在模型中则按刚性连接处理，此外省略平衡配重、司机室等，以质量点的形式施加在相应位置.根据塔吊的结构特点和ANSYS的单位特性正确选择单元类型，选择的单元类型有：(1)主体结构如标准节、起升臂、平衡臂等采用Beam188单元；(2)拉杆采用Link180单元；(3)省略的大质量部件如平衡配重则采用Mass21单元.在进行网格划分时，将Beam188单元的长度控制在0.2m，以保证计算精度.有限元模型中弹性模量E=210GPa，泊松比μ=0.3，密度ρ=7 800kg/m3.在有限元模型中，塔身最下端施加全约束，附墙与建筑物相连的一端释放绕竖直方向的转动，由于附墙与塔身之间存在绕竖直方向的转动，且塔身可轻微上下窜动，所以附墙与塔身的耦合点分别释放绕竖直方向的转动及竖直方向的移动[18].

为了与前文进行对比分析，塔吊载荷情况完全一致，不考虑起升冲击系数、起升动载系数等[19].

分别选取模型中标准节i的Ai点和Bi点附近的一个单元，提取其应力，如表3所示.

表3　有限元分析求得的各标准节应力汇总表

注：单位：MPa

4对比分析

将经验算法、理论受力分析和有限元分析结果进行对比分析，以验证经验算法的准确性.表4为三种方法求得的各标准节应力汇总表.由于有限元分析结果最接近实际情况，所以分别将经验算法和理论受力分析的结果与有限元分析的结果进行对比，分别求出偏差值和偏差率，偏差值和偏差率均取绝对值.

表4　三种方法求得的各标准节应力汇总表

注：“经”表示经验算法求得的结果;“理”表示理论受力分析求得的结果;“元”表示有限元分析求得的结果;“差”表示偏差值;“率”表示偏差率.应力单位：MPa；偏差率的单位：%.

为了更直观地进行对比分析，绘制出Ai点应力对比分析图和Bi点应力对比分析图，分别为图6和图7所示，两图中“经验”表示经验算法求得的结果，“理论”表示理论受力分析求得的结果，“有限元”表示有限元分析求得的结果.

分析表4、图6和图7，可得如下结论：

(1)三种计算方法得到的附墙2以上的标准节14的A14和B14的应力值相差较小，其中经验算法的结果和理论受力分析的结果一致.

(2)附墙2以下的标准节的应力值，经验算法的结果与有限元分析的结果相差较大，其中靠近附墙2的标准节11至标准节13的应力偏差率相对较小，而其他标准节的应力偏差率均大于100%.其中前主弦杆最大应力偏差为A7点的82.7MPa，最大应力偏差率为A7点的818.8%；后主弦杆最大应力偏差为B7点的81.8MPa，最大应力偏差率为B9点的788.1%.造成该结果的主要原因是经验算法中认为附墙2以下塔身的弯矩不变，而通过理论分析和有限元分析可知，由于附墙支反力的存在，塔身弯矩是不断变化的，且附墙2以下塔身弯矩均小于附墙2处的倾覆力矩.

(3)理论分析与有限元分析的结果整体相差较小，其中前主弦杆最大应力偏差为A14点的4.1MPa，后主弦杆最大应力偏差为B8点的8.4MPa.

图6　Ai点应力对比分析图

图7　Bi点应力对比分析图

5结论

为了验证塔吊附墙以下塔身应力工程经验算法的准确性，以某台塔吊为例，分别以经验算法、理论受力分析和有限元分析三种方法进行分析计算，最后对三种分析的结果进行对比分析.

分析结果表明：(1)经验算法有其简便易用的优点，但在某些场合下结果与有限元分析结果存在很大偏差，其中前主弦杆最大应力偏差为A7点的82.7MPa，最大应力偏差率为A7点的818.8%，后主弦杆最大应力偏差为B7点的81.8MPa，最大应力偏差率为B9点的788.1%；(2)理论分析与有限元分析的结果整体相差较小，最大应力偏差是后主弦杆上B8点的8.4MPa.由此表明该经验算法误差较大，需要根据现场附墙条件进行修正，建议如下：(1)在做粗略计算时，建议使用理论受力分析；(2)如需进行精确计算，则使用有限元分析.

参考文献

[1]秦磊.400吨米多吊点水平臂塔式起重机结构设计与分析[D].哈尔滨：哈尔滨工业大学,2013.

[2]LiuQing,ZengYihui.FiniteelementanalysisontowercranebasedonANSYS[C]//The3ndInternationalConferenceonDigitalManufacturing&Automation(ICDMA2012).Shanghai:TransTechPublications,2012:373-380.

[3]LanfengYu.Calculationmethodandcontrolvalueofstatic

stiffnessoftowercrane[J].JournalofMechanicalScienceandTechnology,2008,22(5):169-175.

[4]刘毅.平头塔式起重机起重臂结构强度计算的研究[D].长春：吉林大学,2014.

[5]HouXiao-ting,LIChang-hua.Researchonthethree-dimensionalmodelingandoptimizationofavirtualtowercranebasedon3DSMax,solidworksandEONprofessional[J].InternationalJournalofPlantEngineeringandManagement,2013,18(1):15-19.

[6]R.Mijailovi,G.Kastratovi.Cross-sectionoptimizationoftowercranelatticeboom[J].Meccanica,2009,35(9):599-611.

[7]朱冰,谷立臣,姬鹏斌.QTZ630塔式起重机的有限元动力学分析[J].建筑机械,2011,15(8):103-106,109.

[8]王武奇.QTZ630型塔式起重机结构有限元分析及地震影响研究[D].西安：长安大学,2009.

[9]YongqiangGu,WenfengWang,ShaodongGuo.AnalysisontowercraneunderwindloadbyANSYS[C]//The12thInternationalSymposiumonStructuralEngineering.Hefei:NationalNaturalScienceFoundationofChina(NSFC),2012:709-712.

[10]ZhiSun,NinHou,HaifanXiang.Safetyandserviceabilityassessmentforhigh-risetowercranetoturbulentwinds[J].FrontiersofArchitectureandCivilEngineeringinChina,2009,31:66-74.

[11]赵威威,白朝阳,曹旭阳,等.在役塔式起重机疲劳寿命分析[J].建筑机械,2013,17(1):72-74,77.

[12]王冬明.塔式起重机空间结构动力学分析及动态监测技术研究[D].太原：太原科技大学,2014.

[13]张晓霞,章金成,李东来,等.柔性附着动臂塔式起重机塔身APDL参数化建模及有限元分析[J].起重运输机械,2012(11):74-78.

[14]曹晔,于兰峰,钱佳敏.基于有限元法的柔性附着塔式起重机结构性能研究[J].机械设计与制造,2012(6):50-52.

[15]马俊,罗林.塔式起重机三杆式附墙杆件受力分析[J].建筑机械,2007,11(19):83-84.

[16]张桢,马俊.基于ANSYS的塔式起重机建模与分析[J].建筑机械化,2010(8):58-60,64.

[17]何成忠,刘汉东,王新华.100t造船塔式起重机模态分析[J].起重运输机械,2012(7):43-45.

[18]GB/T13752-92,塔式起重机设计规范[S].

[19]GB/T3811-2008,起重机设计规范[S].

Forcesanalysisontowerbodyoftowercraneafterattachedtowall

LIUJin,HUANGGuo-jian*, LU Li-dong, WANG Xin-hua,

ZHANGZhen,CHENMin

(GuangzhouAcademyofSpecialEquipmentInspection&Testing,Guangzhou510663,China)

Abstract:In order to verify the accuracy of a stress empirical algorithm for tower body of tower cranes after attached to wall,the force situation of tower body of tower crane after attached to wall was acted to improve the accuracy of stress calculation for tower body.Taking a tower crane′s model as an example,firstly,the stress of tower body was calculated by the empirical algorithm,secondly,the force situation of tower body was analyzed to be deduced the stress by theoretical stress analysis,then,more accurate stress of tower body was obtained by finite element analysis,finally,the comparative analysis of the stress values obtained by three methods was done.Comparative analysis results indicate that there was a big deviation between the results of empirical algorithm and finite element analysis,the biggest deviation was 81.8 MPa,and that the results of theoretical stress analysis and finite element analysis were more closer,the biggest deviation was only 8.4 MPa.The error of the empirical algorithm is big,and the empirical algorithm is needed to revise,the theoretical stress analysis and finite element analysis are recommended to use.

Key words:tower crane; attached to wall; tower body; forces acting

中图分类号：TH113

文献标志码：A

文章编号：1000-5811(2015)05-0157-06

通讯作者:黄国健(1981-)，男，广东清远人，高级工程师，博士，研究方向：特种机电设备安全健康监测,guojianhuang@gmail.com

作者简介:刘金(1986-)，男，湖南衡阳人，工程师，硕士，研究方向：仿真分析与风险监测

基金项目：广东省安监总局安全生产重大事故防治关键技术科技项目(2015AQ); 广东省质量技术监督局科技项目(20149702); 广东省珠江科技新星专项项目(2013075); 广东省特种设备科技协作平台科技计划项目(2014SEK003,2014SEK002,2014SEK001)