采用矩阵累乘的自相关矩阵构造*

程 皓，刘 军

(1.成都大学 电子信息工程学院，成都 610106;2.电子科技大学 通信抗干扰技术国家级重点实验室，成都 610052)

1 引言

基于特征值分解(Eigen Value Decomposition，EVD)和奇异值分解(Singular Value Decomposition，SVD)的子空间算法是近年来研究的热门方向，被广泛应用于信号处理、频谱估计、阵列传感器数据估计和其他参数估计［1］等领域。国内外对子空间算法的研究多集中在EVD 和SVD 分解算法的研究上，但由于被分解的自相关矩阵是由各类传感器单次采样得到，决定了其矩阵内采样数较少、受噪声影响较大的特点。由于被分解的相关矩阵采样点数量的先天不足，若通过改造EVD 和SVD 分解算法来实现特征值的提取，其提升效果较为有限。从国内外发表的文献也可以看出，改进EVD 和SVD 分解算法一般是在信号质量较好、信噪比(Signal－to－Noise Ratio，SNR)较高情况进行的，对低信噪比环境下的信号效果不好。究其原因是被分解的相关矩阵样本数不足，对同一矩阵仅依靠算法上的提高不能有效提高信号特征值。对于上述缺点，要解决低信噪比下的特征值分解问题，需要从被分解的矩阵源头入手，通过多次采样、分段相乘的方法，扩大被分解矩阵的样本数，从而抵消噪声在待分解矩阵中所占的比值，达到显著提升信号特征值的目的。

采用相关矩阵分段相乘技术(Matrix Multiplication based Subspace，MMS)构造的矩阵，不仅能像传统方法一样，在信号特征值与信噪比函数之间建立联系，而且能在信号特征值与累积窗口数量之间也建立函数关系。信号特征值既是信噪比的函数也是累积窗口分段数的函数。在低信噪比条件下，仅通过增加分析窗口的分段数量，就能明显区分出信号特征值与噪声特征值。

将新构造的矩阵用EVD 分解，显示出该算法能明显提升信号特征值的特性。新算法能有效提高有用信号特征向量的估计效果，对多用户条件下的用户数检测、码型分离同样有效。

2 数学模型

2.1 相关矩阵数学模型

子空间的相关矩阵R 可以用如下公式表示:

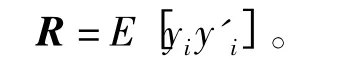
式中，yi代表第i个采用窗口内的采样点数(共M个采样点)，E{·}代表N个窗口内所有数据的平均值。

从上式可以看出，信号特征值的大小仅取决于信噪比的大小，而与统计窗口累积次数的多少无关。由此可以得出结论，传统子空间方法［2］仅仅依靠增加统计窗口个数是无法达到提取信号特征值的目的，若每个采样窗口均处于低信噪比的条件下，信号特征值仍然会湮没在噪声中。

区别于传统子空间对相关矩阵的构造方法，本文提出的构造方法，对R 的建立不再采用R=］的方式，而改用累乘的方法，即通过对采样后的数据分段、累乘，构造出新的相关矩阵。

构造的新型矩阵具备如下特点:

(1)保留了传统子空间方法相关矩阵的特性，能够在信号特征值与信噪比函数之间建立函数关系;

(2)分解后的信号特征值大小与累积窗口数量相关，即信号特征值既是信噪比ρ 的函数也是累积窗口分段数K 的函数;

(3)分析窗口数量越多，信号特征值增长越快，而噪声信号的特征值几乎不随分析窗口数量的增长而增加。当累积窗口数量K 达到一定数量时，能明显区分出信号特征值与噪声特征值。

2.2 直接序列扩频(DSSS)数学模型

下面对本文使用到的各种数学符号作如下定义:{ck，k=0，1，…，P－1 }为用户扩频序列;P 为序列位数(长度);Ts为 符号周期;Te为 采样周期;Tc为码片周期(Tc=Ts/P);t0为 失步时间(采样窗口与实际的符号起止窗口时间差)，见图1;h(t)为信号传输过程中所有信号畸变带来的影响总和，也可以理解为传输链中发射端滤波器、信道滤波器、接收端滤波器和其他信道畸变影响带来失真的卷积，

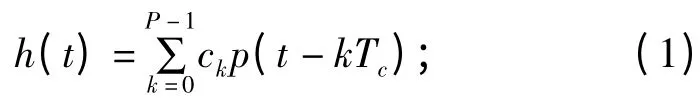
h 为h(t)的矢量表示;s(t)为扩频信号经接收机接收、解调后的基带信号，

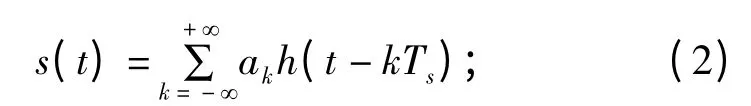
n(t)为噪声;σ2为噪声方差;y(t)=s(t)+n(t)为接收机解调输出含噪信号。

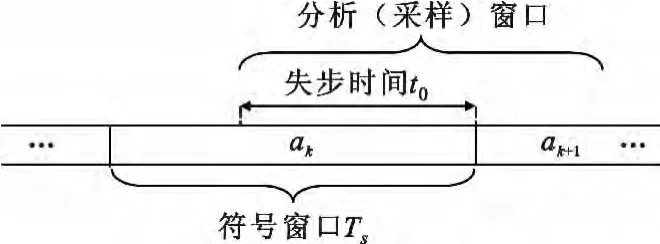
图1 采样时间窗Fig.1 The window of sampling time

对上述变量和后面要推导的公式进行如下限定:

(1)扩频前用户基带信号ak在较长期限内“+1”、“－1”数量大体相等，均值为零;

(2)噪声n(t)为高斯型白噪声，且与信号ak相互独立，完全不相关;

(3)使用循环谱相关方法能够在极低SNR 下计算出码片周期Tc和载波频率f0。本文的仿真条件定于SNR=－30 dB，此时，通过文献［3］可证明方法可行，在该SNR 下可获扩频信号的射频载波频率f0、符号周期Ts和码片周期Tc;

(4)射频载波频率f0可得，需设计相应下变频接收机，通过数控振荡器(Numerically－ Controlled Oscillator，NCO)产生频率为f0的混频信号，对接收机接收到的调制信号进行混频(相乘)，从而下变频到基带;

(5)Tc可得，为了简化算法，可将仿真采样周期Te直接设置成Tc，但此仅为了计算方便，并非必要，即Tc可不知;

(6)Ts可得，将采样窗口周期设置为Ts。

3 累乘算法

根据2.2 节所述，将每个采样窗口时长Ts分为K 段，K 段内包含N个独立计算的窗口，每段单独计算自相关矩阵。K个自相关矩阵相乘后得到新的待分解相关矩阵

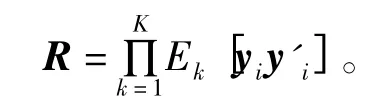
式中，Ek表示第k个N 组窗口的均值;yi表示第k 段、第i个窗口的采样序列，yi为列矢量。

按照上述理论，将采样窗口周期设置为符号周期，由于采样的时间起始点不确定，采样起始点不可能完全与符号起始点在时间上重合，导致单个采样周期内应该横跨两个符号。这里设第一个符合为ak，保持时间t0(t0为失步时间，未知)，设第二个符号为ak+1，保持时间为一个完整符号周期减去上一个符号的保持周期Ts－t0。由于单个采样周期内存在两个符号的不同段，对该采样周期内的相关矩阵分解后，将呈现两个较大的有用信号特征值，该特征值分别表示上述两个符号的前端和后端，而其他特征值均为噪声特征值:

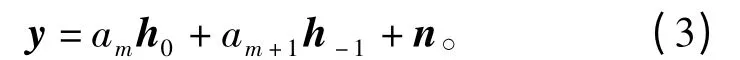
式中，n 表示噪声，为矢量信号;h0=［0，0，…，0］是包含Ts－t0个h(t)值与t0个0 值的矢量;h－1是一个包含Ts－t0个0 值与t0个h(t)的矢量。

根据式(3)可得

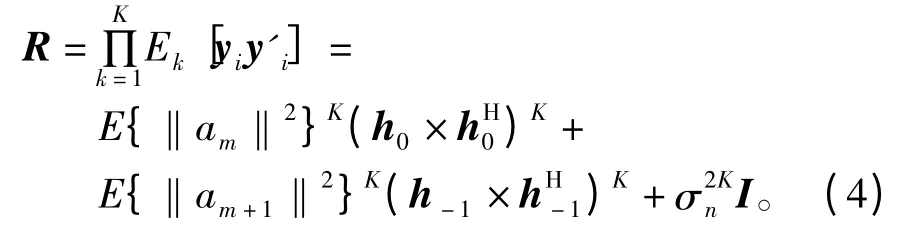
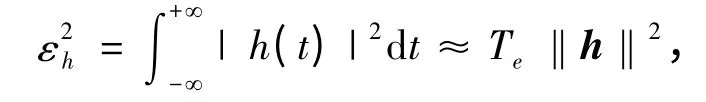
定义

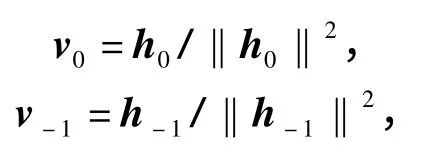
式(4)可改写为

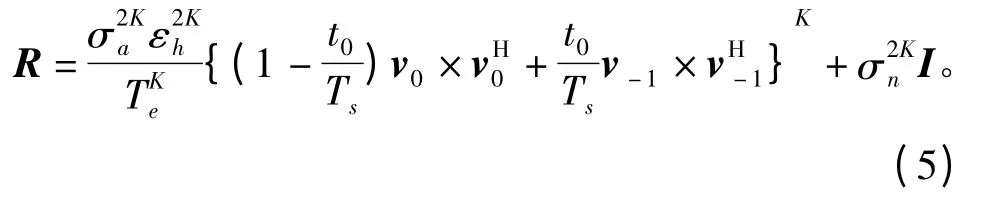
扩频后的信号方差可表示为

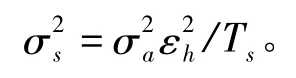
信噪比不采用以dB 为单位的对数表达式，而采用信号与噪声的直接比值，定义如下:

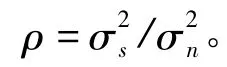
式(5)可进一步改写为

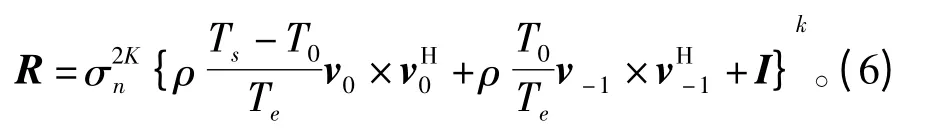
对矩阵R 进行特征值分解，特征值中λ1、λ2为有用信号矢量的两个特征值，其他特征值λi(i≥3)则为表征噪声矢量的噪声特征值，其产生机理是由系统中的各类噪声引起。

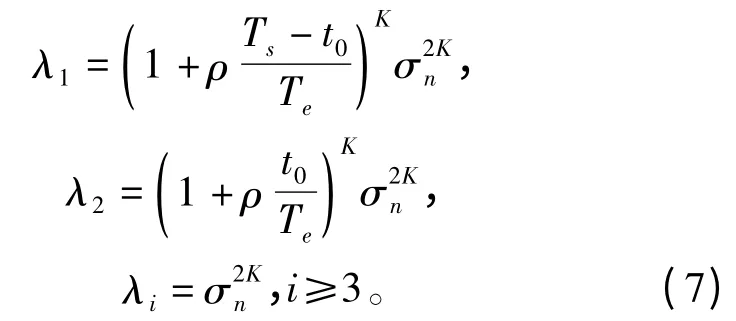
根据式(7)，使用本文论述的累乘构造算法，λ1、λ2不仅与信噪比ρ 有关，同时也是分段数量K的函数，即λ1、λ2是ρ 和k 两者的函数。

为了比较，下面给出传统子空间相关函数构造方法:

式(7)与式(8)之间关系为

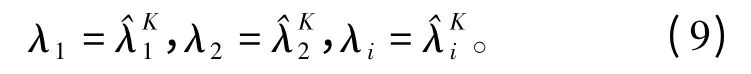
将式(9)按泰勒级数展开，得到

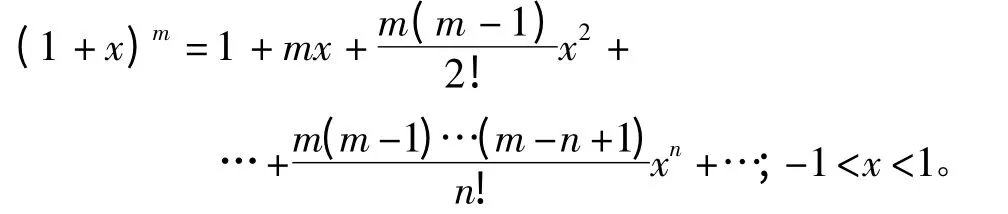
忽略二次及以上项，简化后得到

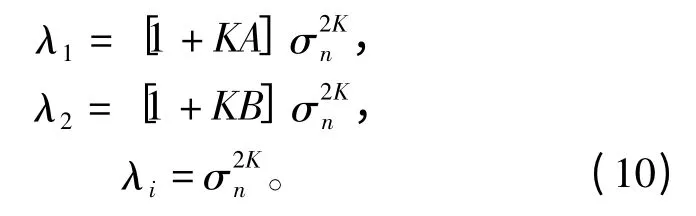
为了简化，这里假设

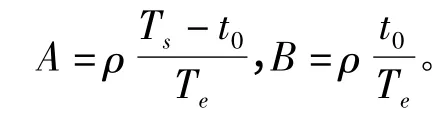
根据式(10)，得到新算法特征值λ1、λ2和λi之间的关系为

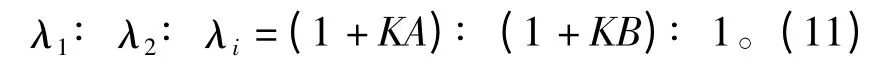
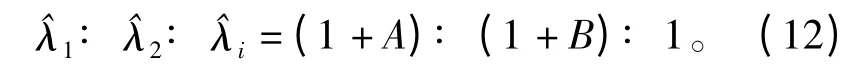
比较式(11)、(12)，在低信噪比条件下，ρ "0，A，A、B "0。此时，使用传统自相关算法构造的矩阵分解后得到的结果，其噪声与两个信号特征值之比趋向于1∶ 1∶ 1(见公式(12))，不能从噪声特征值中有效地辨出信号特征值。而采用MMS 累积得到的相关矩阵，分解后由于K 为一个大的正整数，能有效增加λ1、λ2与其他特征值λi之间的差异。

4 实验与分析

综合考虑算法的计算量、采样样本数和仿真时间，参考文献［3］，本文使用自相关、互相关性非常好的Gold 码作为扩频序列，码长设为63，调制类型设为QPSK，信噪比设为SNR=－30 dB［3］，此时可预先估计出载波频率f0、符号周期Ts、码片周期Tc。此时，ρ=0.001，并设置K ×N=10 000个分析窗口，对算法进行验证。采样周期Te=Tc=Ts/P，采样窗口周期设为Ts，为了方便计算，信道内没有多径干扰，失步系数设定为T0/Ts=0.4，失步时间t0未知，也可通过式(10)得出。

按照上述参数设置，最终分解后的特征值为A=0.037 8，B=0.025 2。

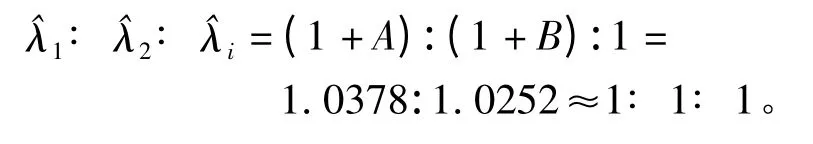
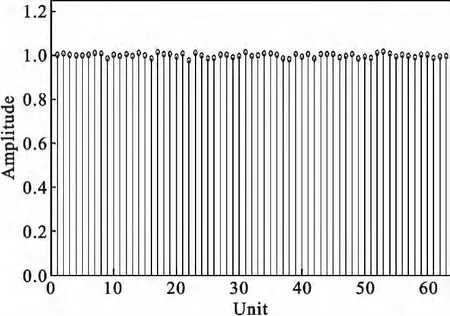
图2 传统EVD 子空间分解后的特征值Fig.2 The eigen values by using traditional EVD subspace decomposition

采用MMS 算法后，设定K=8，N=1250，同样在10 000个窗口条件下进行仿真，结果如图3 所示。λ1∶ λ2∶ λi之间比例关系为

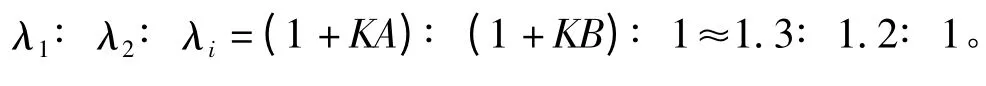
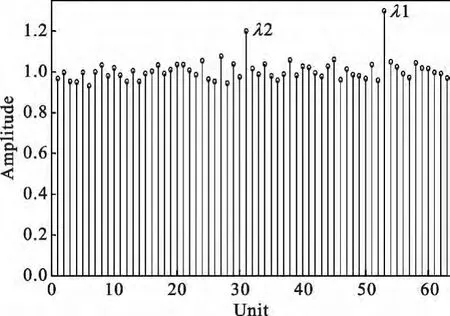
图3 MMS 算法K=8、N=1250 条件下特征值Fig.3 The eigen values based on MMS algorithm when K=8 and N=1250

此时，由于λ1、λ2受K 的系数乘积的扩大，能明显分辨出信号特征值λ1、λ2与噪声特征值λi之间的差异。对比传统方法的图2 和使用MMS 算法的图3可以看出，MMS 算法在低信噪比环境下的特征值提取上有巨大的优势。定量来说，采用MMS 算法后，有用信号特征值A 增大为原来0.3/0.0378≈7.9 倍，有用信号特征值B 增大为原来0.2/0.0252≈7.9 倍。

同样，在不改变总窗口数量10 000的条件下，调整分段数，使K=20、N=500，信号特征值与噪声特征值比例关系理论上应为

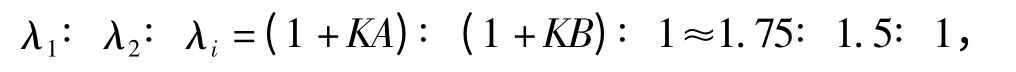
图4 证明了这一理论推导。同理，比较图3 和图4可知，随着K 的增加，信号特征值λ1、λ2与噪声特征值λi的差异越来越明显。但由于总窗口数K ×N保持不变(为10 000)，数量并未增加。K 的增加，导致每段内窗口数N 的减小;样本数N 的减小，导致噪声对分解矩阵R 的影响增大，每个分段求出的相关矩阵特征值的均方差波动变大，所以累乘方法求出的信号特征值的均方差波动比传统算法大。

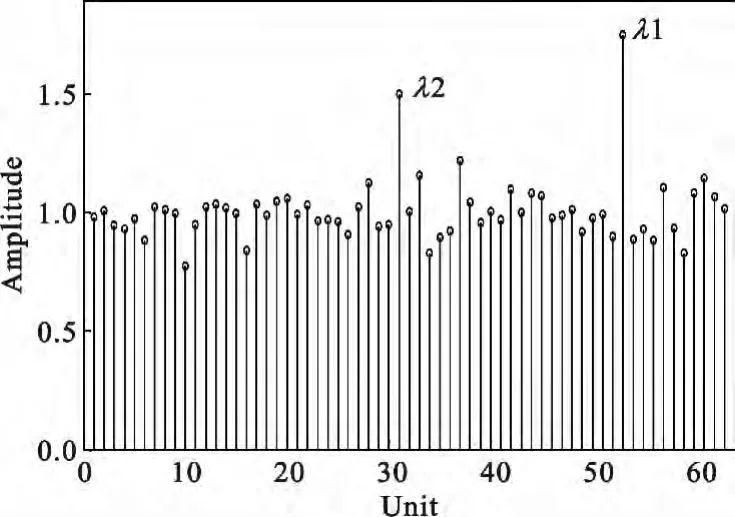
图4 MMS 算法K=8、N=500 条件下特征值Fig.4 The eigen values based on MMS algorithm when K=20 and N=500

为了克服这一缺点，MMS 算法适用于存在足够分析窗口条件下，即样本数足够多，此时N 和K 都能取得一个较大的数值，N 的增大可减小每个相关矩阵的均方差波动，K 的增大可提高信号特征值分辨率。

将信号特征值λ1、λ2代表的特征矢量组合，可得到待估计的Gold 码，组合方法见文献［5］，由于不是本文讨论重点，此处不再详述。

由于该算法的计算结果仅依赖于采样样本数，与计算次数无关，对同一样本进行计算得到的结果相同，所以未采用蒙特卡洛方法进行重复计算。

5 结束语

本文另辟蹊径，从其待分解的信号采样矩阵入手，提出了一种低信噪比环境下的信号相关矩阵构造方法。这一方法重新设计了相关矩阵的构造算法，利用累乘计算，将各个分段矩阵互乘，从而达到在不增大噪声特征值的基础上增大信号特征值的目的，最终达到扩频信号码型分离的目的，计算量与传统构造方法相似。该算法的提出也符合码分多址(CDMA)低信噪比传输特性，具有较大的实用价值。

通过计算机模拟产生的扩频信号作为输入信号，验证了该算法的理论推导的正确性，仿真结果表明，该算法实际计算与理论推导一致，可有效解决低信噪比条件下无法提取扩频用户码序列的问题。文中考虑到计算量的问题，以63 位Gold 码和QPSK信号作为调制信号进行验证，由于算法最终区分的信号与噪声矢量完全是以基带形式表现出来，所以实际工程应用中，该算法不依赖其调制种类，可普遍应用于任何DSSS 信号的码型分离。

下一步工作重点是解决该算法在N 和K 取值均较大情况下保证低波动性和高分辨率的问题。

［1］Veen A，Deprettere E，Swindlehurst A.Subspace－based signal analysis using singular value decomposition［M］.New York:Academic Press，2007:1277－1308.

［2］Gustafsson T，MacInnes C.A class of subspace tracking algorithms based on approximation of the noise－subspace［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，2010，48(12):3231－3235.

［3］Zhang T Q，Lin X K，Zhou Z Z.Estimation method for low SNR DS signal spreading code［J］.Journal of Tsinghua University(Science and Technology)，2005，12(1):1009－1020.

［4］Petre S，Prabhu B，Li J.SPICE:A sparse covariance－based estimation method for array processing［J］.IEEE Transactions on Signal Processing，2011，45(10):451－460.

［5］Nzoza C，Gautier R，Burel G.Blind synchronization and sequences identification in CDMA transmissions［C］//Proceedings of 2004 IEEE Milcom.New York:Academic Press，2004:1384－1390.