基于MATLAB/Simulink的四连杆机构动力学仿真及改进

基于MATLAB/Simulink的四连杆机构动力学仿真及改进

张建军，黄庆学，马丽楠

(太原科技大学重型机械教育部工程研究中心，太原 030024)

摘要：针对四连杆机构的动力学仿真，提出了一种通用化的改进方案。只需输入连杆机构的部分初始参数，再执行一个脚本程序，即可进行四连杆机构的动力学仿真。此外，额外提供了一种求解机构位置解的新方法。输入一组容易获取且误差较小的初始角度参数，再执行一个基于牛顿辛普森算法的m函数文件，即可得到连杆机构的位移曲线与其相应的误差曲线。这不仅为求解机构位置解开辟了新方法，而且还提供了精度比较高的初始值参数，进一步保证了动力学仿真的可靠运行。

关键词：四连杆机构；动力学仿真；通用性改进

收稿日期：2015-01-06

基金项目：山西科技创新团队项目(20131006)；山西省自然科学

作者简介：张建军(1987-)，男，硕士研究生，主要研究方向为机电系统控制及其自动化。

中图分类号：TG659文献标志码：B

1四连杆机构动力学数学建模及仿真模型

1.1运动学部分

在对四连杆机构进行动力学分析之前，需先进行运动学分析，分析结果主要包括以下3个矢量方程：位置方程、速度方程及加速度方程[1-3]。在用矢量法建立机构的位置方程时，需将构件用矢量来表示，并做出机构的封闭矢量多边形[4]，如图1所示。由矢量多边形：

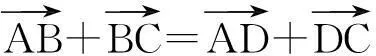
得其复数表达式：

r2eiθ2+r3eiθ3=r1eiθ1+r4eiθ4

(1)

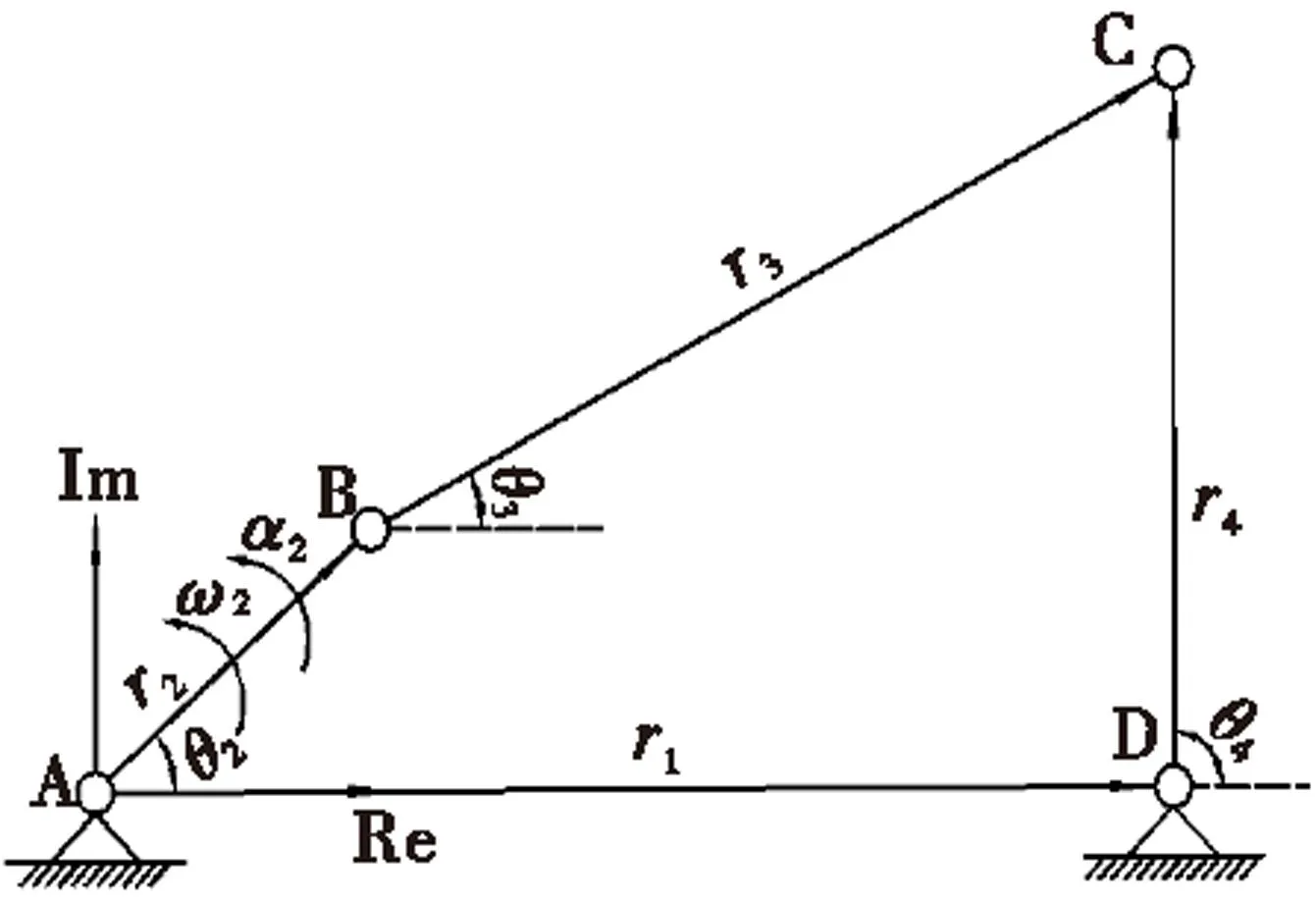
图1　四连杆机构运动简图

利用欧拉公式将式(1)展开，有：

(2)

式(2)是关于θ3、θ4非线性超越方程组，其解由三角函数的关系可求出，但该解法却不适合计算机编程实现，现采用数值解法，并借助MATLAB工具编程实现。对位置方程组(2)，根据求解非线性超越方程的数值解法——牛顿辛普森算法[5-6]，编写相应的位置求解函数m文件，求出四连杆机构的位置初始值。

得到位置初始值后，接下来需求解机构的速度初始值。对式(2)求两次导数，依次得到该机构的速度与加速度方程，这里直接给出其相应的矩阵表达式，即式(3)和式(4).

(3)

(4)

把位置初值代入式(3)，求得速度初值。根据式(4)，编写m文件并搭建Simulink模型，如图2所示，crank.m与rrrki.m分别为曲柄和从动杆组的运动仿真模块。用已求得的位置、速度值作为相应积分模块的初始值，设置好仿真时间，即可进行运动学仿真。

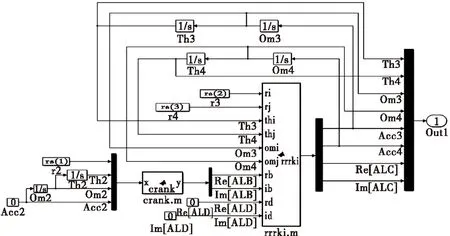
图2　运动学仿真Simulink模型

1.2动力学部分

在运动学分析的基础上，对该机构进行动力学分析。先对图1中四连杆机构中的活动构件进行受力分析，如图3所示。列出相应的力平衡方程，如式(5)~式(7).

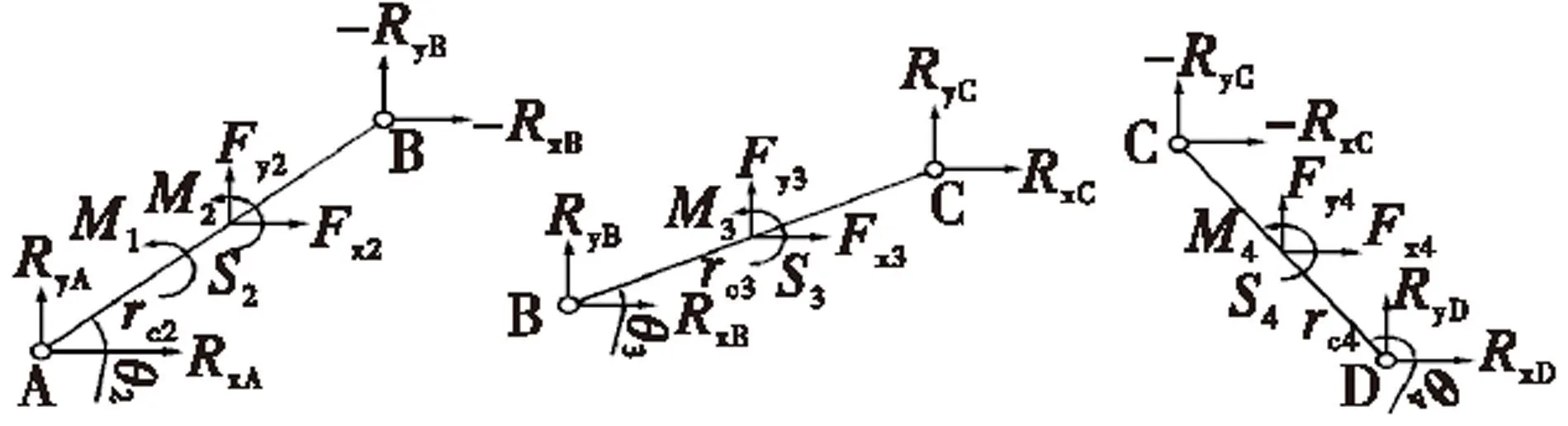
图3　各活动构件的受力分析图

原动件AB的力平衡方程：

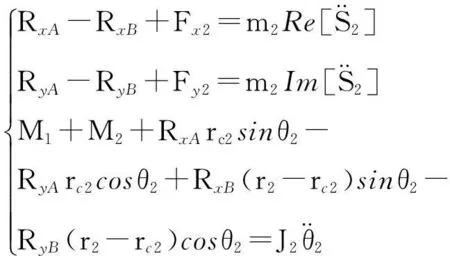
(5)

连杆BC的力平衡方程：

(6)

从动件CD的力平衡方程：

(7)

式(5)~式(7)中，m2～m4及J2～J4分别为活动构件2~4的平动与绕质心Si(i=2，3，4)的转动惯量，Fxi、Fyi以及Mi(i=2，3，4)分别为活动构件质心处所受的外力在实虚轴上的分力以及外力矩，ri与rci(i=2，3，4)为各活动构件的杆长及质心位置值，M1为施加在原动件AB上的平衡力矩，其余符号参考图3.

为便于计算机编程，将式(5)~式(7)整理成矩阵形式(8)与式(9)：

式(8)为原动件AB的力平衡方程(5)的矩阵形式，式(9)为从动件BC及连杆CD的力平衡方程(6)、(7)的矩阵形式。结合该机构的运动学仿真模型，根据式(8)与式(9)，建立四连杆机构的动力学仿真模型，如图4所示，式(8)与式(9)分别用来构建曲柄动力学仿真模块crankdy.m与从动杆组动力学仿真模块rrrrdy.m：

设置图4中各模块的值，即可进行仿真。通过仿真发现，积分模块的初始值参数对整个仿真有着决定性的作用。然而，这些初值的获得，需要之前逐次调用位置求解函数以及角速度求解函数。如果Simulink模型文件设置有变化(比如常数模块改变)，还得重新求取位置与速度的初始值，这将大大增加仿真前期的工作量[7-10]。因此，仿真的通用性不强，有必要对原来的仿真进行改进，使其函数调用灵活且重复修改量少，本文的下一节将提供这些思想的MATLAB实现。

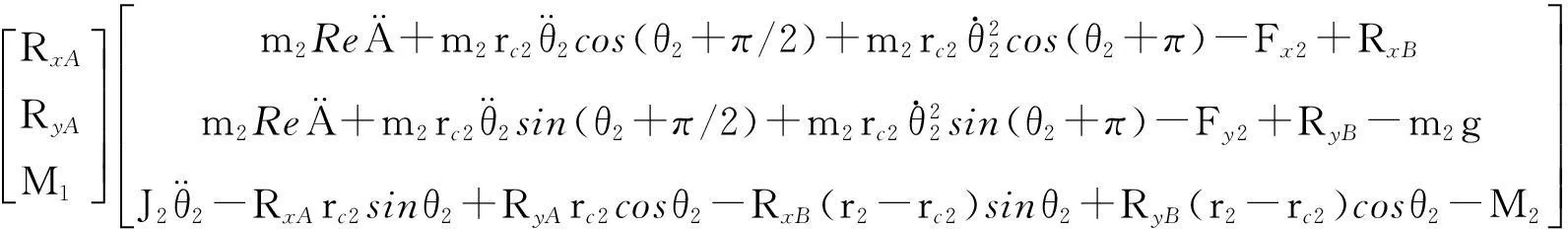
(8)

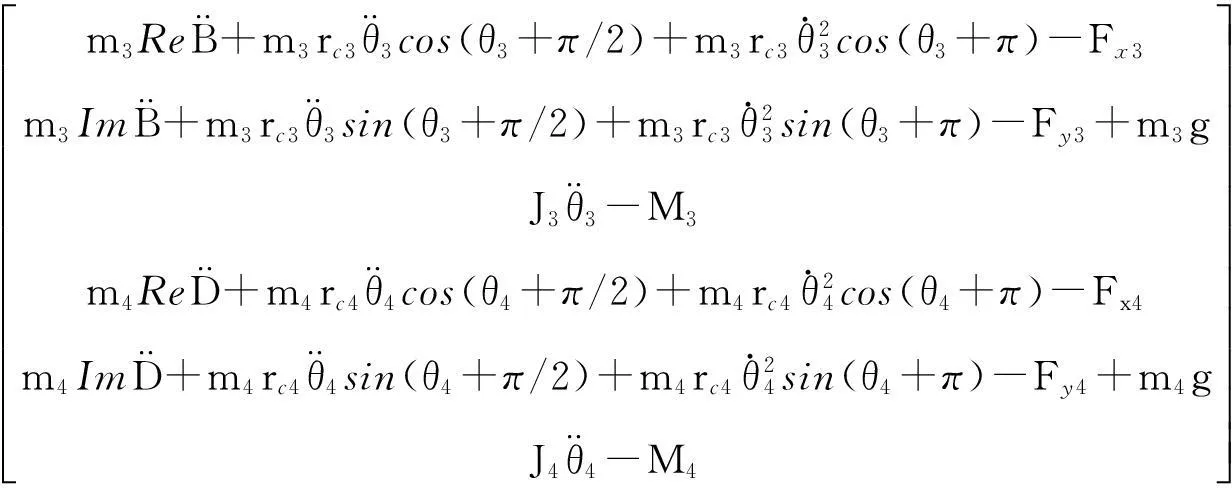
(9)

图4　动力学仿真Simulink模型

2四连杆机构运动学仿真通用性的改进及其实例验证

所谓的通用性是指，对任意的四连杆机构，只需在MATLAB命令窗口给出杆长矩阵、角度初值矩阵、原动件运动及动力参数等，通过调用一段程序代码，即可实现动力学仿真。为了提高原仿真的通用性，本节提供一种改进方案，并给出相应的实例。

2.1改进方案及其MATLAB实现

首先，需先设置Simulink模型文件中的积分模块的初始值。在Simulink中有两种方法建立其仿真的初始条件。第一种，就是直接在相关属性栏中填入数字。遗憾的是，这种方法对于更复杂的初始条件会变得非常笨拙，且不适合通用化程序设计的要求。另一种方法是为MATLAB环境变量设置初始值，即用变量名代替数字，该变量的值由MATLAB工作空间提供，因此需在仿真前在MATLAB的命令窗口给同样变量名的变量赋值。使用第二种方法，很容易在MATLAB环境中用一系列命令改变初始值，而无需在每次初始条件改变时，返回Simulink模型图，修改相应模块的设置。本节将采取第二种方法。

其次，也是比较重要的，编制一个脚本m文件，以调用其他m函数文件。该m文件中用代码依次调用了处于同一工作目录的位置初值求解函数、速度初值求解函数以及Simulink模型文件。通过m文件的内部调用，符合模块化编程思想，调试方便，减少了重复编程量。此外，为了给程序调试带来便捷，考虑到要单独调用某个m函数文件，故将以上各m文件单独保存在同一工作目录，而没有将其作为子程序整合到脚本文件中。

2.2实例佐证

如图3所示，铰链四连杆机构各构件的几何尺寸为r1=1 200 mm，r2=400 mm，r3=1 000 mm，r4=700 mm；质心为rc2=200 mm，rc3=500 mm，rc4=350 mm；质量为m2=1.2 kg，m3=3 kg，m4=2.2 kg；绕质心的转动惯量J2=0.016 kg/m2，J3=0.25 kg/m2，J4=0.09 kg/m2，构件4的工作阻力矩M4=100 N/m，顺时针方向，其他构件所受外力和外力矩均为零，且不考虑摩擦。构件2(即原动件)以等角速度ω2=10 rad/s逆时针旋转。

设置完成后，在MATLAB命令提示符下输入：

th=[0，45，100，0]；rs=[0.4，1，0.7，1.2]；

om20=10；

该品种由福建省泉州市农业科学研究所（福建省泉州市晋江市池店镇泉安北路，邮编：362212）和云南省农业科学院经济作物研究所培育。

r10=[1，0.7，0.5，0.35，3，2.2，0.25，0.09，0，0，0，0，0]；

cr10=[0.4，0.2，1.2，0.016，0，0，0，0，0]；ts=1；Ini；

并回车即可。其动力学仿真结果如图5和图6所示。

图5依次为连杆3和从动件4的角位移、角速度和角加速以及铰接副C的加速度分量随时间的变化曲线，图6依次为铰接副A的水平与竖直方向的分力和曲柄AB上的平衡力矩及其所做的功随时间的变化曲线。

综上所述，为提高动力学仿真程序的通用性，本节仅通过在外部调用一个脚本文件Ini.m，实现了对任意四连杆机构的动力学仿真。整个操作过程简单且通用性强，如果仿真条件有变化(如仿真时间或者初始位置预估值变化)，只需在外部命令上进行修改，而无需修改相应的m函数文件或者Simulink模型文件。

3四连杆机构的位置解求解新途径

上一节介绍了动力学仿真的通用化改进——只要给定连杆长度及初始位置等参数，即可得到整个机构的动力学动态参数。该机构的动态位置解，是反馈的加速度值经过积分模块处理后的输出，该输出又作为下一步仿真的输入，如此循环下去，最终得到全程的位置解曲线。本节将介绍另外一种求解机构位置信息的途径，该方案以一组容易获得且误差较小的初始位置解为起点，将原动件等间距地旋转一周，通过反复使用牛顿辛普森方法，进而求出若干位置的位置解。

以图1的四连杆机构为例，其初始条件以容易获取为选择标准。编写一个MATLAB函数文件fourbar.m，在代码中建立以下循环：曲柄角度θ2从0°开始，以2°为步长，递增至360°；对应每个θ2值调用位置函数求解位置角。

在MATLAB命令提示符下，输入以下代码：>>clear；th=[045100]；rs=[0.41 0.71.2]；n=180；theta=fourbar(th，rs，n)；执行函数文件fourbar.m，将得到一个关于机构位置解和误差的矩阵theta，以及从动件角位移及其误差的曲线图，如图7所示。

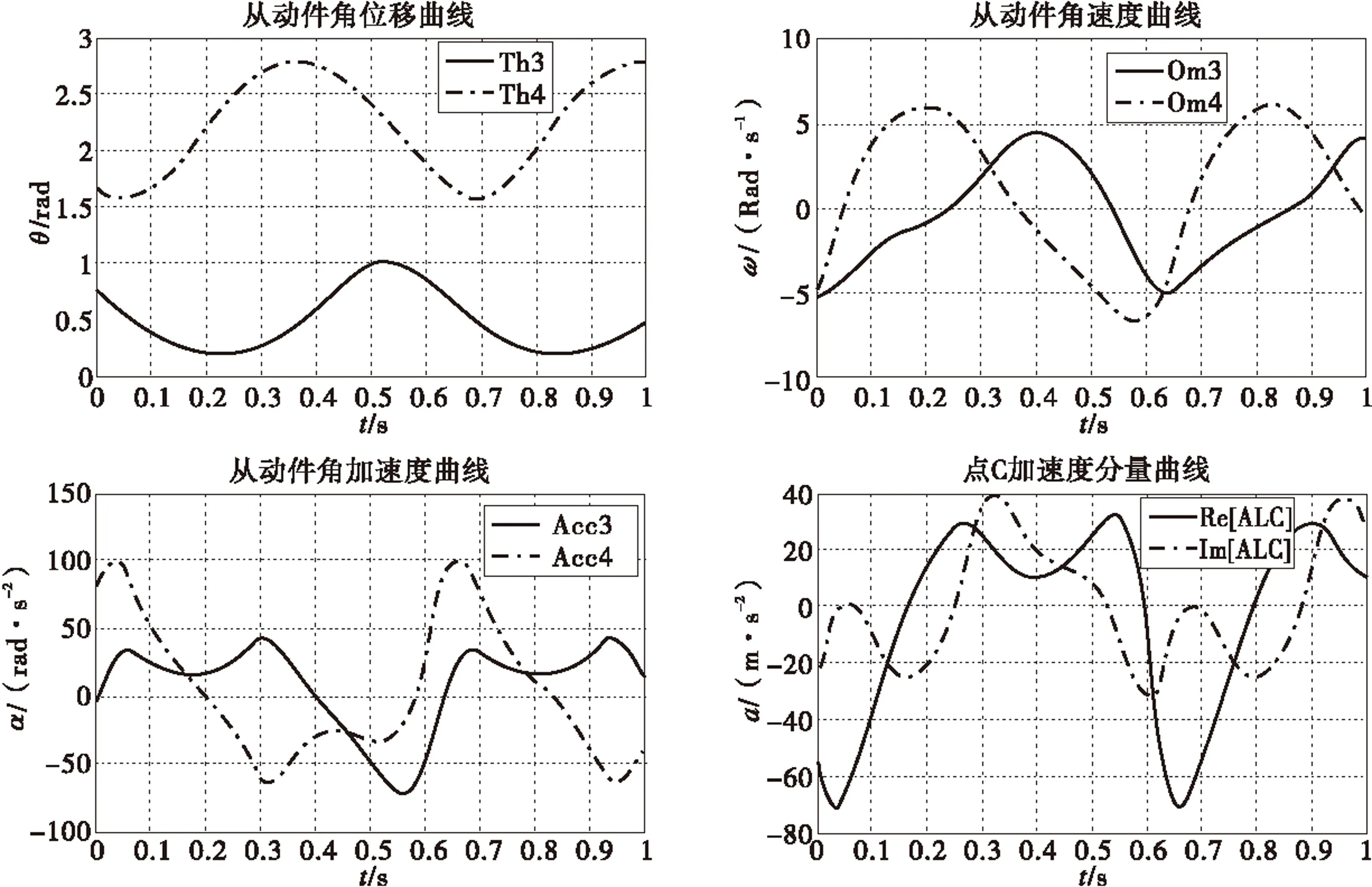
图5　四连杆机构运动学仿真结果

由图7的误差曲线可知，从动件角位移误差在±1.5°范围。此外，可以改变输入的n值，修改步长得到更为精确的仿真曲线。通过查询该仿真曲线或者矩阵theta(可以编写m文件实现)，可以获取任意位置的位置解，为该机构以其他位置为起点进行仿真提供可靠的初值。

4结束语

本文依次推导了与四连杆机构动力学学相关的数学模型， 并且建立其仿真模型进行了相关分析与改进。改进后的动力学仿真模型，操作简单，调试方便，通用性强。

图7　从动件角位移及误差仿真曲线

此外，本文还提供了四连杆机构位置解的另一种求解途径，通过执行脚本文件fourbar.m发现，这种方法的结果误差也比较小且操作简单，而且能给仿真前提供可靠的初始值。

总之，与以往的对四连杆机构动力学仿真的程序相比，本文设计的程序充分利用了MATLAB软件的编程特点—m文件之间的内部调用的便捷性，大大提高了程序的通用性与操作简易的程度，这给方便地修改参数以适应任意四连杆机构的动力学仿真提供了高效的通道。

参考文献：

[1]李明磊，贾育秦.基于MATLAB/Simulink的齿轮五杆机构运动仿真研究[J].太原科技大学学报，2009，30(1)：59-62.

[2]武娟，任家骏，吴凤林，等.基于MATLAB软件中SIMULINK的机构运动仿真[J].机械工程与自动化，2004，124(3)：4-6.

[3]徐梓斌.六杆机构运动学仿真的MATLAB实现[J].煤矿机械，2006，27(4)：617-618.

[4]孙桓，陈作模，葛文杰.机械原理[M].北京：高等教育出版社，2006.

[5]曲秀全.基于MATLAB/Simulink平面连杆机构的动态仿真[M].哈尔滨：哈尔滨工业大学出版社，2007.

[6]GARDNER J F.机构动态仿真：使用MATLAB和Simulink[M].周进雄，张陵，译.西安：西安交通大学出版社，2002.

[7]陆凤仪，孙占营，徐格宁.基于杆组理论的连杆机构运动精度及运动仿真研究[J].太原重型机械学院学报，2003，24(1)：57-61.

[8]薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京：清华大学出版社，2002.

[9]王永超.基于MATLAB的机构运动学仿真方法及其比较[J].计算机仿真，2004，21(8)：81-84.

[10]王芳，张海燕.基于Simulink的连杆机构运动学仿真[J].机械设计与研究，2004，20(2)：35-37.

Improvement for Dynamical Simulation of Four-bar Linkage

Mechanism Based on MATLAB/Simulink

ZHANG Jian-jun，HUANG Qing-xue，MA Li-nan

(Heavy Machinery Ministry of Education Engineering Research Center，Taiyuan University of

Science and Technology，Taiyuan 030024，China)

Abstract：To improve dynamical simulation program of four-bar linkage mechanism，a general scheme for better simulation was studied.After providing the required initial parameters，one script will be run to proceed dynamic simulation program.Besides，one more new solution will be introduced to confirm the dynamic positions of mechanism.After inputting some starting angles， a function file based on Newton-Rapson algorithm was executed to draw displacement and its error diagrams.The new method not only solves the location problem of driven links，but also provides more precision initial angles when starting simulation from any other positions to make sure dynamic simulation successful and precise.

Key words：four bar linkage mechanism，dynamical simulation，improvement for generality