结合昌马水库渗压计观测数据探讨一元线性回归法在坝体渗压分析中的应用
2015-12-24张鹏举
结合昌马水库渗压计观测数据探讨一元线性回归法在坝体渗压分析中的应用
张鹏举
(甘肃省疏勒河流域水资源管理局,甘肃 玉门735211)
摘要:本文采用一元线性回归对昌马水库2002—2012年渗压计观测结果进行了统计分析,建立了水库水位与孔隙水压力之间的线性关系,并采用相关系数对数据进行稳定性检验,同时对存在线性关系的线性模型给予一定的置信度。应用所建模型的预测功能,可对观测值进行预测,得到不同水位时渗压计监测结果的预测区间,为以后的日常观测提供一定的参考范围。
关键词:渗压计; 水位; 异常值; 一元线性回归; 相关性
中图分类号:TV698.1
Discussion on the application of unary linear regression method
in dam seepage pressure analysis based on Changma Reservoir
osmometer observation data
ZHANG Pengju
(GansuShuleRiverBasinWaterAuthority,Yumen735211,China)
Abstract:In the paper, unary linear regression method is adopted for statistic analysis of Changma Reservoir osmometer observation results from the year 2002—2012. Linear relationship between the reservoir water level and pore water pressure is established, and correlation coefficient is adopted for stability test on data. Meanwhile, linear model with linear relationship is given with certain confidence. Prediction function of the established model is applied for predicting the observations. Prediction intervals of osmometer monitoring results at different water levels are obtained, thereby providing certain reference scope for subsequent daily observation.
Key words:osmometer; water level; abnormal value; unary linear regression method; correlation
1概述
大坝安全监测是了解大坝运行状态及发展趋势,保证大坝安全运行的重要措施,也是检验设计成果、检查施工质量和认识大坝各种参量变化规律的有效手段。目前,在水库大坝的安全监测系统中,渗流压力是大坝安全性态和运行状态的最直观、最有效的反映,也是大坝安全监测的最主要项目之一[1]。
通过一定的数学方法对所采集的各类监测数据进行处理和分析,可以综合判断工程的安全性,并及时发现隐患和排除险情,从而确保正常施工和建筑物的安全运行[2]。在回归分析方法中,一元线性回归分析以其成熟的原理、高可信度的预测结果、运用的简洁性等优点,在工程技术经济领域有着十分广泛的应用[3]。
2基本资料
昌马水库是甘肃省河西走廊(疏勒河)农业灌溉暨移民安置综合开发项目的龙头工程,总库容1.934亿m3,是以农业灌溉为主,兼顾工业供水、水力发电和防汛等综合利用的大(2)型水利枢纽。共埋设15支渗压计,经过多次运行,P1号渗压计出现异常。因此,此次分析数据中未包含P1号渗压计数据。
3数据处理与模型建立
3.1Gurbbs准则
服从正太分布的测值序列若存在异常值,则有
(1)
(2)
式中xi——序列监测测值;
xd——待检验的实测值;

Sn——序列监测测值的标准差;
α——Gurbbs准则的临界值表中的显著性水平。[4]
3.2模型建立
3.2.1一元线性回归模型
a.一元线性回归基本模式。设两个变量x与y之间存在如下关系:
(3)
式中α,β,σ2——未知参数;
x——普通变量。
式(3)称为一元线性回归模型,由于ε是随机变量,故y也是随机变量,易知
(4)

(5)
式(5)为y关于x的回归函数。
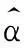
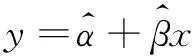
(6)
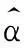
b.最小二乘法。设一个容量为n的样本(x1,y1),(x2,y2),…,(xn,yn),记
(7)
选取适当的α、β,使Q(α,β)之值达到最小,为此,分别求Q(α,β)对α及β的偏导数,并令之为零,得
(8)
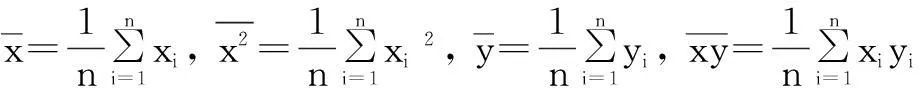
(9)
这个方程组称为正规方程组,可解得α与β的最小二乘估计为
(10)
由此可得y对x的回归方程:
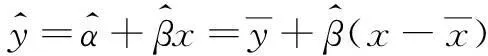
(11)
3.2.2回归方程的显著性检验
采用数学统计的方法检验两个变量之间是否一定存在线性相关关系,即应对线性模型(11)提出如下假设:
(12)
|β|的值体现了自变量x对y的影响程度。如果检验过后拒绝H0,就可以认为x对y有明显的作用,所得线性回归方程有实用价值;如果拒绝H0,则所得到的线性回归方程无意义。

(13)
称ST为离差平方和,将其进行分解:
不难证明交叉项等于零,若记
(14)
(15)

SE——剩余平方和或残差平方和,它是实际观察值yi与回归值yi的离差平方和,反映了随机因素对y取值的影响。
相关系数检验法,取统计量
(16)
其中,R为样本相关系数,R体现x与y线性相关的程度。如果给定显著性水平α,可查表求得临界值c,当|R|>c时,可拒绝H0,于是H0的拒绝域为

(17)
可以证明:F检验法、t检验法、相关系数检验法这三个检验法彼此是等价的。此次统计分析采用相关系数检验法对模型进行了检验。
3.2.3预测与控制
对于x的任一值,由式(3)有
(18)
若取其回归值
(19)
可以证明
(20)
对于置信度1-α,由
得y0的置信度为1-α的预测区间为
(21)
(22)
4模型应用
此次分析以昌马水库水位为自变量x,渗压计观测得到的孔隙水压力为因变量y。首先应用Gurbbs准测对渗压计测得的孔隙水压力数据进行处理,剔除异常数据。其次通过式(3)~式(22)得到一元线性回归模型,分析水库水位与孔隙水压力之间是否存在线性关系,并利用模型预测功能得到对应置信区间,并且对大坝未来沉降趋势可以进行简单的预测。
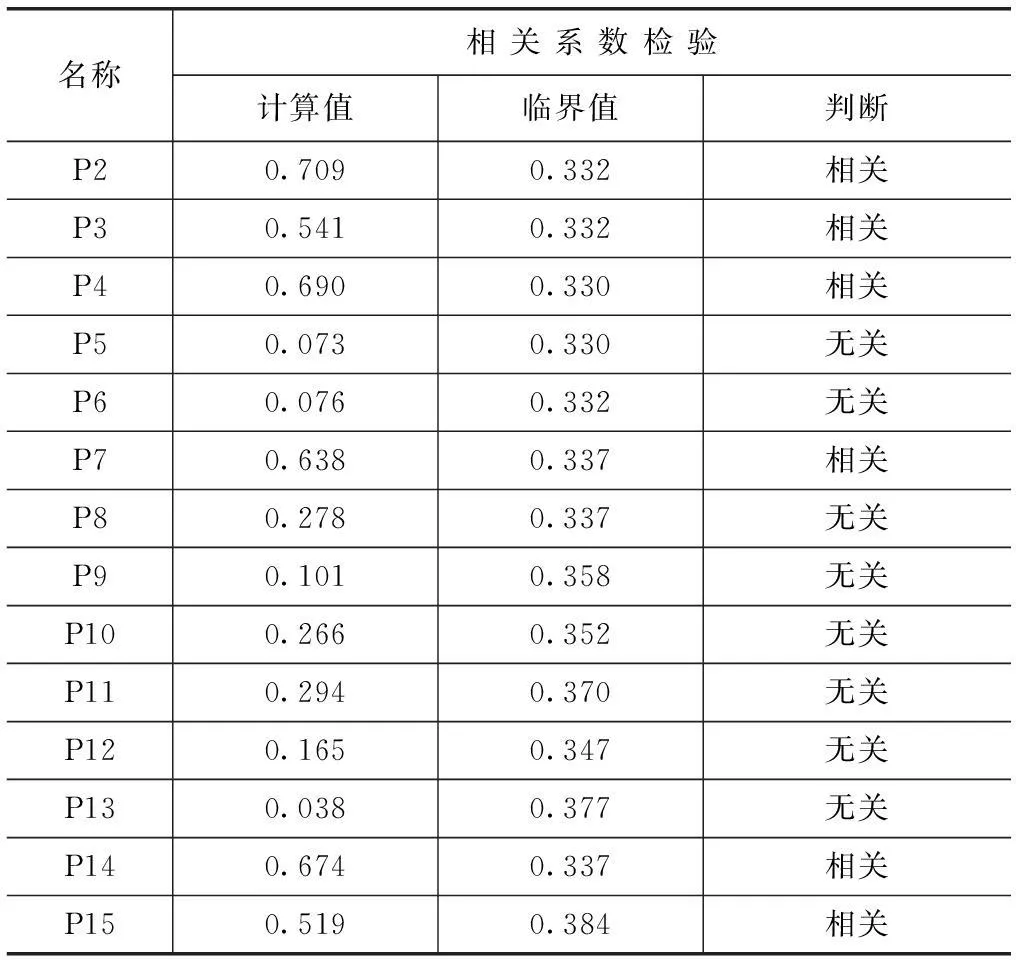
检验统计表
由上表可以看出,数据稳定性良好,所建立的一元线性回归模型正确。其中,P5、P6、P8、P9、P10、P11、P12、P13渗压计的监测结果与水库水位是线性无关的,可以判定水库水位对以上渗压计的监测结果并没有多大影响。P2、P3、P4、P7、P14、P15存在一定的线性关系。相关系数越接近于1因变量与自变量之间的相关关系越好,存在一定线性关系的渗压计,其相关系数最大值为0.709(P2),最小值为0.519(P15),相关系数平均值为0.638。
5结语
渗压计观测数据的误差来源比较复杂,利用此次建立的一元线性回归模型对昌马水库水位与渗压计监测结果进行分析,结合水库初步设计及近年来渗流观测资料,得出结论:昌马水库经过多年运行之后,水库大坝的心墙局部渗流是稳定的。利用数据模型中的回归区间预测,可为以后的日常观测提供参考范围。因此,此次观测模型的应用,不仅可以有效地避免误差引起的观测数据不准确,提高了观测精度及效率,而且为以后通过观测数据来定量分析和预测大坝变形规律和发展趋势、适时监控大坝的运行状态提供了有效的保障。
参考文献
[1]李富强.大坝安全监测数据分析方法研究[D].杭州:浙江大学,2012.
[2]高伟. 简析大坝安全监测对水库安全运营的重要性[J].河南水利与南水北调,2013(22):31-32.
[3]陆晓珩,高延兵,瞿建农,任卫礼. 一元线性回归方法的应用[J].中国测试,2012,38(S1):11-13.
[4]周中汉,王汉江,李梅,郭定和.利用DPS剔除测量数据中的异常值[J].计量技术,2007(10):61-63.
[5]刘晓石,陈鸿建,何腊梅.概率论与数理统计[M].北京:科学出版社,2005.

