协同粒子群优化算法的改进与仿真

侯 翔，蒲国林

（四川文理学院 计算机科学系，四川 达州635000）

0 引 言

最初的PSO 算法虽然结构简单，却无法保证算法收敛，为此许多改进的PSO 算法应运而生［1］。比较典型的是线性惯性权PSO 算法［2］和模糊惯性权PSO 算法［3］，文献［4］提出了具有收缩因子PSO 算法等，但以上算法往往会出现过早收敛现象。

通常情况下，PSO 算法具有易陷入过早收敛的缺陷，同时，易受到维数灾难 （curse of dimensionality）的困扰。针对该问题，Van等［5］借鉴遗传算法的合作协同进化算子，采用降维的方法，提出了一种协同PSO 算法 （CPSO）。虽然CPSO 算法在解决某些问题的同时可以提高优化过程的收敛性能，但该算法会出现伪最小值现象，并且不能保证收敛到局部或全局最优。文献 ［6］将随机PSO 方法引入到CPSO 中，提出了一种以概率1收敛到全局最优的改进协同PSO 算法 （ICPSO），该算法的全局收敛性主要由随机PSO 保证，CPSO 主要用于提高算法的收敛速度。

本文根据协同进化原理，通过对传统PSO 算法进行协同优化处理，设计了一种改进的协同PSO 算法。该算法通过对所有粒子经历的最优位置采用协同优化策略，为群的全局最优提供一个参考，以提高算法的收敛性能。

1 协同PSO 算法

对于经典的PSO 算法，通常是由一个或若干个群组和而成，而每个群又包含许多粒子，对于群中的粒子，其位置信息由与其对应的n 维矢量来表示，表示问题可行解。粒子根据一定的飞行策略不断地改变自身的速度和方向，根据自身的记忆功能和信息分享机制求出问题最优解［7，8］。

该进化策略将n维空间作为一个整体，在每次优化中，将依据适应值的优劣，同时更新解向量的n 个分量。该策略使得粒子群逐渐移向问题的最优解，但是该策略在有些分量上出现 “进两步，退一步”的问题。例如对于n 维解空间，适应值定义为f（x）＝，当n＝3时，显然问题的最优解是 （0，0，0）。假设第k 次搜索的最优解是g＝（0.1，5，0.1），f（g）＝25.02，显然解的第1个分量和第3个分量已经比较接近全局最优解；在k＋1次搜索中，群中适应值最小的粒子位于 （3，1，3）处，其适应值为19，根据上述进化策略，粒子群搜索到的最优解将更新为g＝ （3，1，3），即使解出第2个分量已经很接近全局最优，但是也可能使原来已经很接近最优解的分量远离最优解。鉴于PSO是一种随机优化算法，因此，上述情况是有可能发生的。

在PSO算法对最优解搜索的过程中，针对其可能发生的“进两步，退一步”的现象，Van等根据合作协同进化遗传算法的主要思想，提出了一种降维分解的PSO 算法，并称之为CPSO （cooperative PSO）算法，该算法的主要思路如下：

对于n维空间的优化问题，构造n 个粒子群，每个群代表n 维空间的一个分量，并且由m 个粒子组成。每次迭代，所有粒子采用常规的PSO 策略更新位置和速度值，并根据适应值最小原则，分别更新每个粒子所经历的最优位置pbest和n 个粒子群所经历的最优位置gbest，再将这n个gbest联合组成一个n 维向量作为问题最优解的近似值。

由于计算适应值需要完整的n 维向量，而每个粒子只对应n维向量的一个分量，因此为了优化n 个1维粒子群，必须构造一个n 维向量。Van等将前一次迭代得到的问题最优解的近似值作为一个常量P，在考虑第i个粒子群时，逐一用m 个粒子替换P 的第i 个分量，计算其适应值，最小适应值对应的粒子为该群本次迭代的最优值。

考虑n 维解向量的各分量可能存在某些关联，Van等［5］在此基础上又提出了CPSO－Sk算法，即根据某个分裂因子 （split factor），构造若干个k 维粒子群，每个粒子代表解空间的连续k个分量。算法的执行过程与CPSO 类似，这里就不再详细阐述。

虽然CPSO算法试图通过降维方法解决前面提到PSO 算法中的“进两步，退一步”问题，也取得了相应的效果，但并没有将解向量各维分量相互之间有可能存在的关联关系考虑在内，因此通过CPSO算法获得的各维分量的最优值的联合，并不能等同于问题的最优解。文献 ［6］研究表明CPSO算法容易产生伪最小值，甚至根本无法进入问题最优解的邻域，因此该算法无法保证收敛到局部或全局最优。

2 改进的协同PSO 算法

虽然单纯的CPSO 不是一种合适的优化算法［9，10］，但将CPSO 算法中的协同优化的思想用到常规的PSO 算法中，可以改善算法性能。为此，本文提出了一种改进CPSO算法，为了叙述的方便及不引起歧议，以下将本文提出的算法记为COPSO，该算法的主要思路如下：

算法由一个粒子群构成，群中粒子的位置信息由一个n维矢量来表示，其表示问题可行解。通过迭代，粒子根据常规PSO 算法更新位置和速度矢量，并根据适应值最小原则，更新各自所经历的最优位置pbest和整个粒子群经历的最优位置gbest。

随后，借鉴CPSO 中的协同优化方法，对所有粒子的历史最优位置pbest进行逐维优化，具体优化过程详见算法伪代码，并形成一个粒子群参考全局最优位置G。

最后，比较两全局最优位置gbest和G，如果G 的适应值更优，则用G 替换gbest，完成后进入下一次迭代。图1为COPSO 算法伪代码。

图1 COPSO 算法伪代码

图1的第9行提出要更新粒子的位置和速度，但没有具体指明用哪种方式更新，这表示可以用任何常规的PSO算法更新粒子位置和速度。

3 仿真实验

为了说明COPSO 算法的性能，本文分别将其用于惯性权PSO［11］及带收缩因子的PSO 算法［12］中，也就是在这两种常规PSO 算法中加入本文提出的对粒子经历的最优位置进行降维协同优化策略，并对加入前后的算法性能进行比较实验。本文选取了3个常用的标准非线性测试函数，它们分别是：

（1）Sphere函数

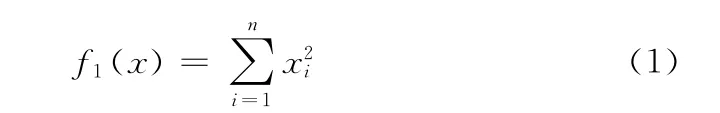
（2）Rastrigrin函数

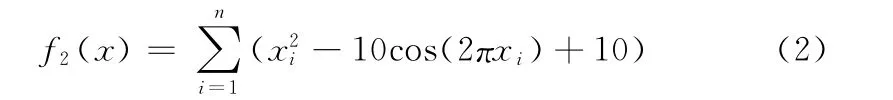
（3）Griewank函数

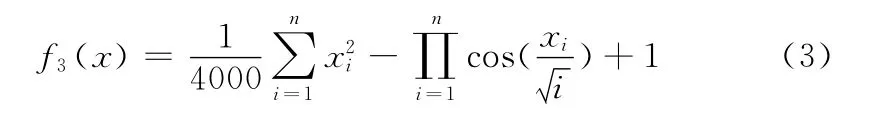
式中：x ＝（x1，x2，…，xn）维实向量。

上述3个标准函数的最小值均为0，其中Sphere函数是单峰值函数，其它为多峰值函数。在所有实验中，上述3个函数均取30维，并设定群中微粒子的数目为30。惯性权PSO 算法的参数设置为：w＝0.9－0.5t/tmax，c1＝c2＝2，其中t为当前进化代数，tmax为最大进化代数；带收缩因子的PSO 算法的参数设置为：k＝0.729，φ ＝4.1。

对微粒子的初始值采用不对称的选择方式，它们的初始值范围、目标精度、微粒子速度和位置的极限值见表1，所有实验的最大进化代数为5000次。

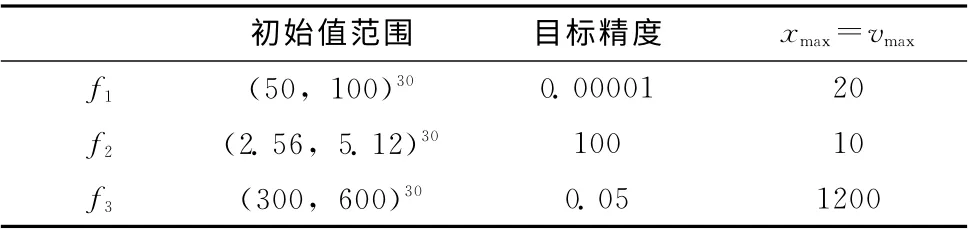
表1 各测试函数的参数范围

本文所有仿真实验均在MATLAB中完成，MATLAB可以显示的最小数值为eps＊realmin＝4.9407×10－324，即再小于该数值，则在MATLAB 中显示为0。为保证实验结果的可信度，每种算法对每个测试函数的优化均进行了20次独立的仿真实验，实验结果如表2、图2、表3、图3所示。

表2是COPSO 与惯性权PSO 两种算法的实验结果比较统计表。表中IWPSO 表示惯性权PSO 算法；It＿av、It＿max、It＿min分别表示在20次独立实验中，达到目标精度所需的平均迭代次数、最大迭代次数及最少迭代次数；F＿av表示经过5000次迭代后所能达到的解的平均函数值（或适应值）；表中的0表示实际值小于MATLAB的显示的最小数值，可以认为算法优化已达到全局最优。

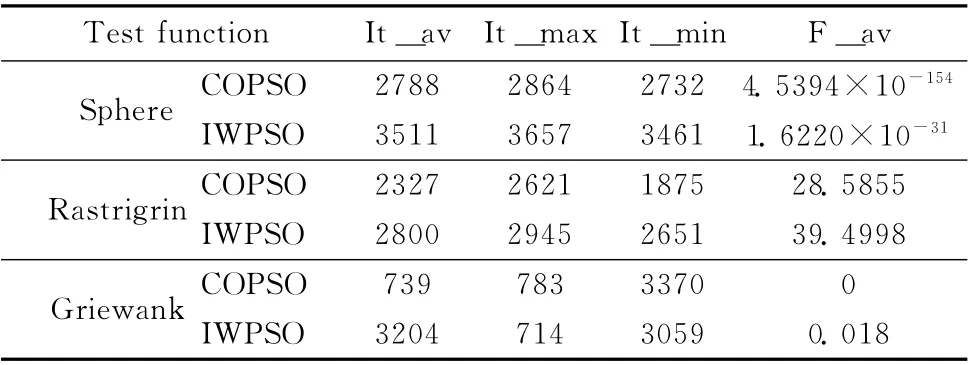
表2 COPSO 与惯性权PSO 比较实验结果

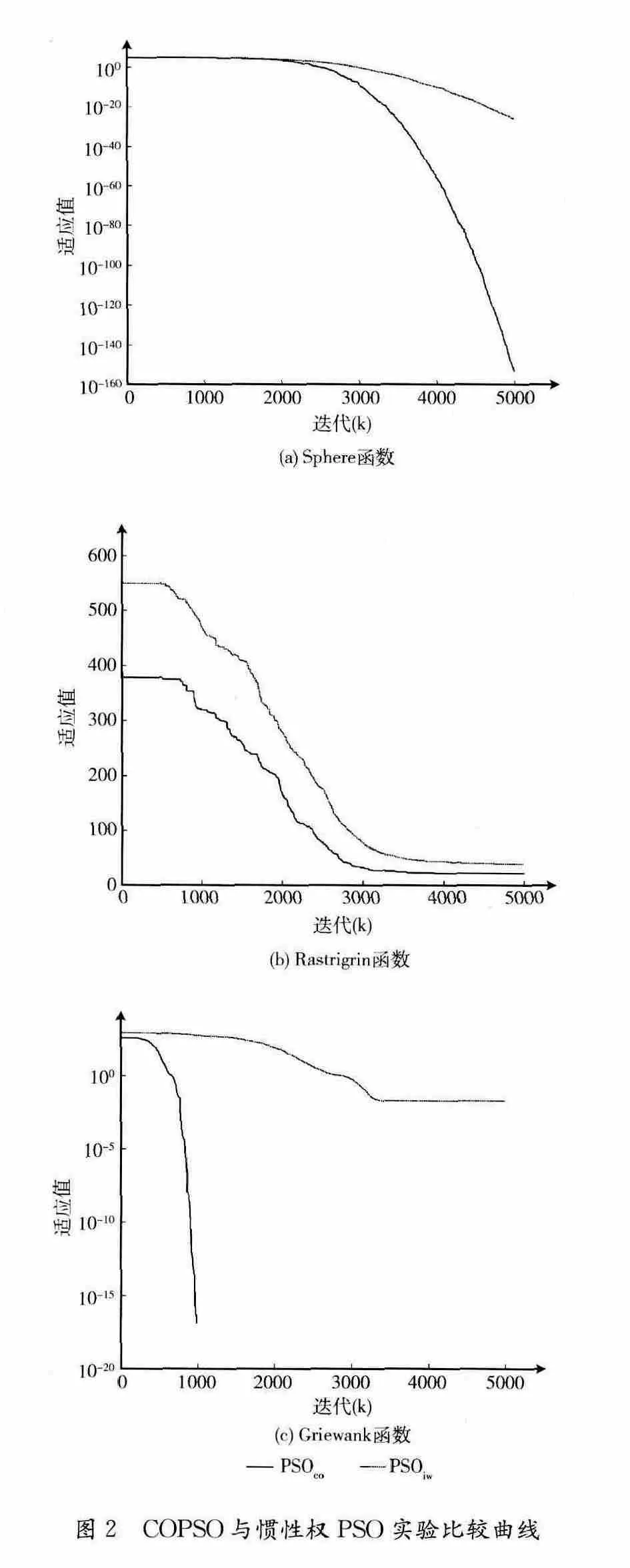
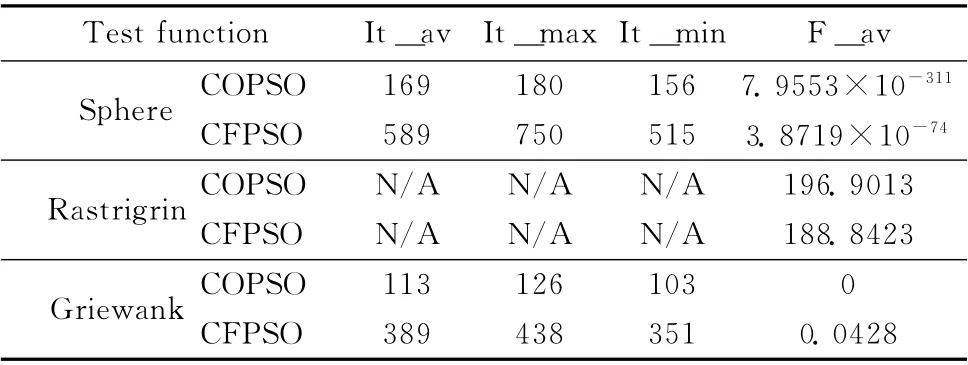
表3 COPSO 与带收缩因子PSO 比较实验结果

从表2可以看出，COPSO 对于3个测试函数的优化性能均有所提高。对于Sphere函数，与惯性权PSO 相比，COPSO 首先将达到目标精度的迭代次数提前了723次，相当于将收敛速度提高了近20%；其次，经过5000次迭代，COPSO 的精度提高了10120多倍。对于Rastrigrin 函数，COPSO 虽然在收敛速度上有明显提高，但最终的收敛精度并没有显著改善，进一步说明COPSO 有利于改善PSO 算法的收敛速度，但还不能保证算法收敛到全局最优。COPSO 的性能在对Griewank函数的优化中表现最为突出，它使得算法收敛速度提高了4倍多，而且达到全局最优。

为了更清晰地显示实验过程，本文将表2中的比较实验过程绘制成曲线如图2所示。图2包含3组曲线图，分别表示对3个测试函数进行优化的实验过程。每一个曲线图中的两条曲线分别表示两种算法在20次独立实验中解的平均适应值的变化过程。其中PSOco表示COPSO 算法，PSOiw表示惯性权PSO 算法。

从图2可以看出，COPSO 使得算法收敛过程明显加快，图2 （a）和图2 （c）表明COPSO 在算法收敛精度上有显著提高。图2 （b）表明两种算法针对Rastrigrin函数没有显著差别，但仍然可以看出，在初始阶段，COPSO 的收敛速度明显加快。

表3是COPSO 与带收缩因子的PSO 两种算法的比较实验结果的统计表。表中CFPSO 表示带收缩因子的PSO算法；N/A 表示在所有20次独立实验中均未能达到设定的目标精度；表中其它标注与表2相同。另外，表中最后一行数据表示带收缩因子PSO 对Griewank函数的优化结果，由于在20次独立实验中，有4 次实验均未能达到目标精度，所以该行数值为其它16次实验的统计结果。

从表3中可以看出，对于Sphere函数和Griewank 函数，COPSO 无论在收敛速度还是收敛精度上都有显著提高，而且从达到目标精度的最大及最小迭代次数上看，COPSO 算法更为稳定。但对Rastrigrin函数，COPSO 没有显示优势，甚至在算法精度上还略逊于CFPSO。

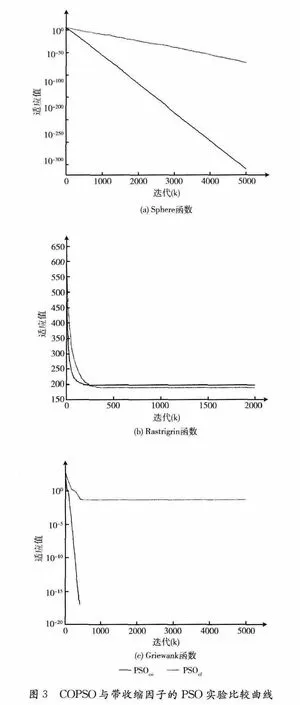
表3所示实验的过程曲线如图3所示，图中PSOcf表示带收缩因子的PSO，其它标注与图2 相同。由于对于Rastrigrin函数，两种算法在所有40 次独立实验中，迭代2000次后解的适应值均不再变化，所以为了显示算法初期的变化，只绘制了前2000次迭代的过程。从图中可以明显看出COPSO 算法在对Sphere函数和Griewank函数优化时的显著优势。值得一提的是，根据对表3 数据的分析，对于Rastrigrin 函数，COPSO 算法甚至不如带收缩因子的PSO，但是从图3 （b）可以看出，COPSO 还是可以明显提高算法在初始阶段的收敛速度。

由仿真结果可以得出，COPSO 算法能够明显地提高了收敛速度和收敛精度，甚至可以收敛到全局最优，这也再次说明COPSO 算法不能保证收敛到全局最优。

4 结束语

本文根据协同进化基本原理，通过在常规PSO 算法中加入简单的降维协同优化策略，以提高常规PSO 算法在高维优化问题中的性能。大量仿真比较实验结果表明，本文所提出的改进协同PSO 算法有利于提高算法收敛的速度，对某些问题可以显著提高算法的收敛精度，甚至可以收敛到全局最优。但是COPSO 算法无法保证算法收敛到全局最优，这也是需要进一步研究的地方。

［1］Cooren Y，Clerc M，Siarry P.MO－TRIBES，an adaptive multiobjective particle swarm optimization algorithm ［J］.Computational Optimization and Applications，2011，49 （2）：379－400.

［2］Chen WN，Zhang J，Chung HS，et al.A novel set－based particle swarm optimization method for discrete optimization problems［J］.IEEE Transactions on Evolutionary Computation，2012，14 （2）：278－300.

［3］Shi SY，Eberhart R.Fuzzy adaptive particle swarm optimization ［C］//Proceedings of the Congress on Evolutionary Computation，2001：101－106.

［4］Clerc M，Kennedy J.The particle swarm－explosion，stability and convergence in a multidimensional complex space ［J］.IEEE Transactions on Evolutionary Computation，2002，6（1）：58－73.

［5］Frans VDB，Andries PE.A cooperative approach to particle swarm optimization ［J］.IEEE Transactions on Evolutionary Computation，2004，8 （3）：225－239.

［6］Shi YH，Eberhart R.Empirical study of particle swarm optimization ［C］//Proceedings of the Congress on Evolutionary Computation，1999.

［7］LIU Zhixiong.Logistics vehicle scheduling optimization based on particle swarm optimization ［J］.Wuhan University of Science and Technology，2012，32 （6）：615－618 （in Chinese）.［刘志雄.基于粒子群算法的物流车辆优化调度研究 ［J］.武汉科技大学学报，2012，32 （6）：615－618.］

［8］Monay F，Gatica－Perez D.Modeling semantic aspects for CROSmedia image indexing［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，29 （10）：1802－1817.

［9］Xu Xinli，Hao Ping，Wang Wanliang，et al.Multi－agent dynamic scheduling method and its application to dyeing shops scheduling ［J］.Computer Integrated Manufacturing Systems，2012，16 （3）：612－620.

［10］Feng Hongkui，Bao Jinsong，Jin Ye.Hybrid particle swam optimization algorithm for multiple vehicle dragging goods problem ［J］.Computer Integrated Manufacturing Systems，2012，16 （7）：1428－1436.

［11］Zhou XC，Zhou ZX，Zhou KJ，et al.Remanufacturing closedloop supply chain network design based on genetic particle swarm optimization algorithm ［J］.Journal of Central South University of Technology，2012，19 （2）：482－487.

［12］HAN Pengfei，SUN Zhanlei，ZHAO Gang.Improved discrete particle swarm algorithm and its application in the study of eating machine assembly task scheduling ［J］.Graphics Sinica，2013，34 （1）：60－65 （in Chinese）. ［韩鹏飞，孙占磊，赵罡.改进离散粒子群算法及其在吃机装配任务调度中的应用研究 ［J］.图学学报，2013，34 （1）：60－65.］