基于自适应混沌粒子群的聚类算法

顾忠伟，徐福缘

（1.上海理工大学 管理学院，上海200093；2.浙江科技学院 经济管理学院，浙江 杭州310023）

0 引 言

经典的聚类算法［1－6］有模糊c 均值、K－means、PSO－c均值、CURE等。其中模糊c均值聚类算法的研究和应用相当广泛。为了使模糊c 均值聚类算法的性能更加优越，许多学者基于不同角度对它进行了改进。如Jingwei Liua等提出了一种新型的基于核化的模糊c－均值聚类算法，对聚类中心的权重系数进行了修正，并利用标准Iris数据库和正常肿瘤基因芯片上的数据样本进行测试［7］；Du－Ming Tsai等对距离度量的方法进行了改进，并将聚类中心与质心结合起来研究，提出了一种新的基于距离度量的模糊c－均值聚类算法［8］；Dan Li等提出了基于最近邻间隔的模糊c－均值聚类算法，该算法通过使用数据的分布间隔时间表示最近邻集，对部分缺失数据集进行深度挖掘［9］。

模糊c－均值聚类算法在处理小规模低维数据集时效果良好，但是，该算法在处理高维数据集时表现出自适应性不强、易陷入局部极小值和聚类效果不理想等缺陷，针对此问题，本文提出了一种基于自适应混沌粒子群的聚类算法，理论分析结果和实验结果表明，其聚类效果优于现有的C－means、标准PSO 等算法。

1 粒子群算法

粒子群算法，也称粒子群优化算法 （particle swarm optimization，PSO）［10，11］。算法中的每个粒子表示所求问题的一个解，通过迭代更新来寻找最优解。粒子通过位置和速度来进行更新，粒子的好坏程度由一个合适的适应度值来决定。PSO 算法相对于其它优化算法而言具有简单、容易实现、所需参数较少等特点。标准粒子群算法的数学描述如下所示：

假设粒子群X ＝（X1，X2，…，Xn）由n个粒子组成，每个粒子的搜索空间为D 维，群体中第i个粒子表示为Xi＝（xi1，xi2，…，xid）。设第i个粒子在寻优过程中的最优位置为Pi＝（pi1，pi2，…，pid），群体中最优的粒子表示为Pg＝（pg1，pg2，…，pgd）。每个粒子的速度和位置按如下公式进行更新

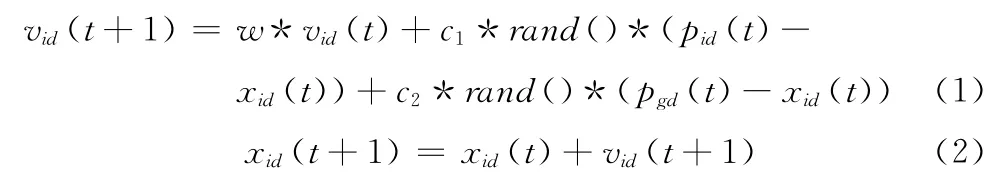
式中：w 为惯性权重，c1和c2为加速因子，rand（）为 ［0，1］之间随机数；i＝1，2，…，n；d＝1，3，…，D；t为迭代次数，每个粒子根据初始条件按式 （1）和式 （2）进行迭代更新。从上面的表达式可以看出，每个粒子的飞行速度由3部分来决定，第一部分为粒子自身的历史飞行速度vid（t）；第二部分为粒子对自身最优位置的思考，表示粒子按照自身的认知水平朝最优方向飞行；第三部分为社会环境部分，表示其它粒子群体对自身位置的影响。因此，从本质上讲，粒子的运动轨迹由粒子自身部分、认知部分和社会环境部分来引导。

2 基于自适应混沌粒子群的聚类算法

2.1 编码方式

模糊c均值聚类算法是利用隶属度函数将种群中的个体划归为某个类别的算法，该算法首先将数据划分为c个模糊类，然后利用公式求出每个模糊类的聚类中心，最后将隶属度函数和聚类中心结合起来使模糊目标函数最小化。由于模糊c均值聚类算法的目标函数存在许多局部极小值，所以在迭代的过程中，目标函数很可能会陷入局部极小值，从而使算法无法找到全局最优解。特别是当聚类的数据向量比较多并且维数较大时，模糊c均值聚类算法更易呈现早熟现象。为了克服这种缺点，本文将改进的粒子群算法与模糊c均值聚类算法进行整合，构造出自适应混沌粒子群聚类算法。自适应混沌粒子群聚类算法的编码方式如下：

设X ＝｛x1，x2，…，xn｝为数据集样本，簇的数目为c，采用实数编码方式，每个粒子用一个三维矩阵X［i］［k］［d］表示，其中i＝1，2，…，n；k＝1，2，…，c；d＝1，2，…，D。对数据集样本各簇中心vj进行初始化，然后赋值给各个粒子X［i］［k］［d］。

结合两种算法的特点，新算法适应度目标函数值设为

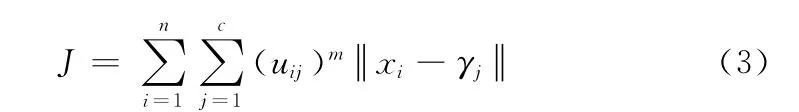
式中：m——模糊聚类的权重指数，uij——粒子X［i］［k］［d］归属于第j类的模糊隶属度，uij可表示为

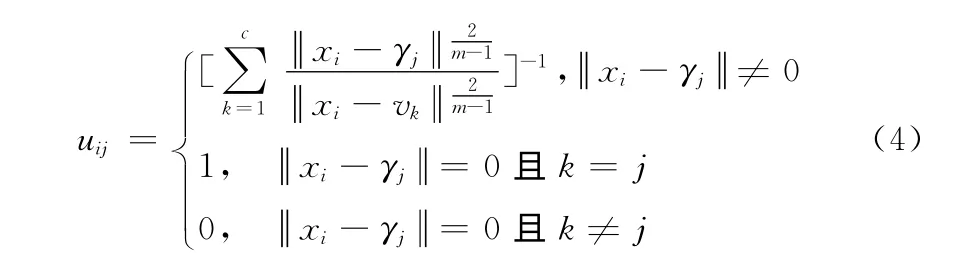
式中：γj——第j类的聚类中心，γj可表示为

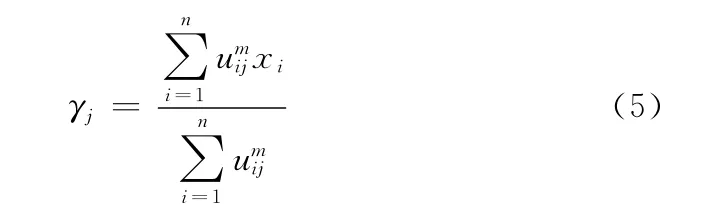
2.2 自适应粒子群聚类

PSO 算法在寻优的过程中，每个粒子都试图朝着最优的方向飞行，当某个粒子找到一个最优位置时，在认知部分和社会环境部分的影响下，其它粒子将迅速向其靠扰，因此算法很容易进入局部最优的状态。式 （1）中加速因子c1和c2设置不当的情况下，算法进入局部最优的状态更为明显，此时算法将会出现早熟的现象。针对此问题，本文对粒子群的加速因子c1和c2进行自适应动态设置，使c1和c2的大小根据粒子群的实时状态进行调节。

在第t次迭代时，整个粒子群的平均适应度fp（t）可以表示为

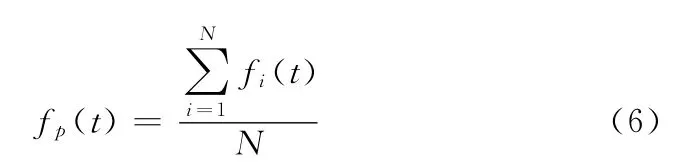
式中：fi（t）——第i个粒子在第t 次迭代时的适应度值。fg（t）是当前粒子群中占据最优位置的粒子适应度值，那么加速因子c1和c2可分别表示为

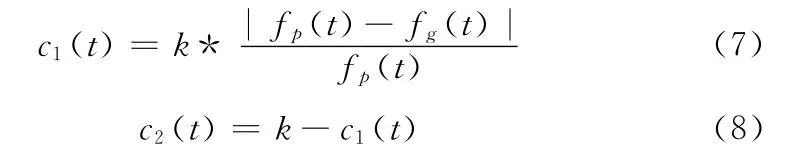
式中：k为协调因子。通过对粒子的寻优特点进行研究，可以发现粒子的初速度对PSO 算法的性能也有所影响。当粒子的初速度过大时，粒子很可能会飞跃局部区域，从而错过搜索局部区域的机会；当粒子的初速度过小时，粒子又将陷入局部区域，从而使算法出现早熟现象。针对这种现象，本文将对粒子的初始速度进行处理。具体的调节方案如下

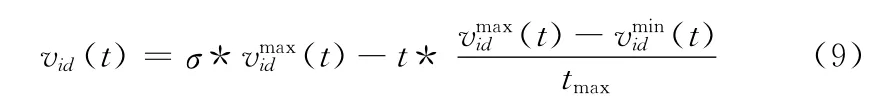
式中：σ——权重系数，vmaxid（t）——第d维的最大值，vminid（t）——第d 维的最小值，tmax——迭代的最大数目。经过改进后，粒子的速度可表示为

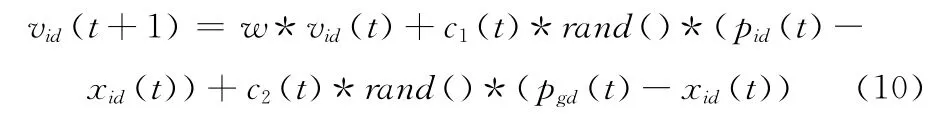
2.3 混沌搜索与边界缓冲墙

混沌是非线性复杂系统中广泛存在的一种现象，混沌优化能够在预先设定的范围内对特定群体进行扰动和遍历。为了增强粒子群的多样性，可以利用混沌优化对粒子群进行扰动，以混沌搜索替代随机搜索，最终使整个粒子群进入最优平衡状态。本文利用Logistic混沌系统，迭代产生相应的混沌序列，Logistic混沌系统的定义如下所示

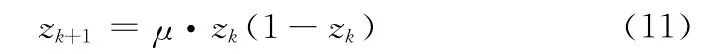
其中，zk∈（0，1）为实值序列，k＝0，1，2，…，n，本文取μ＝4。设扰动量Δx ＝（Δx1，Δx2，…，Δxn），混沌扰动范围为［－xmax，xmax］，将zk的各个分量载波到扰动范围内，则

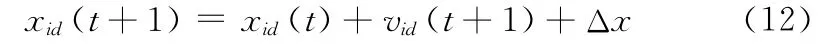
粒子群经过混沌扰动后，不仅种群的多样性得到提高，而且全局搜索能力得到大大的增强。与此同时，粒子的位置和速度有可能会超越其最大值。为此，传统的方法通常是预先将粒子的位置和速度设定在一定的范围内，使超过负边界和正边界的粒子都限定在边界上。传统方法操作简单且计算量小，但是这种预先设定固定极值的做法会带来较大的误差。为了避免这种缺陷，本文将利用边界缓冲墙对越界粒子进行处理。边界缓冲墙的思想如下

若xid（t）＜ad，则xid（t）的值为

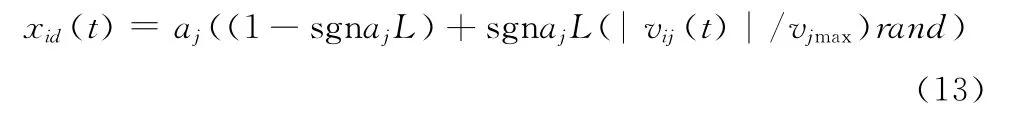
若xid（t）＞bd，则xid（t）的值为

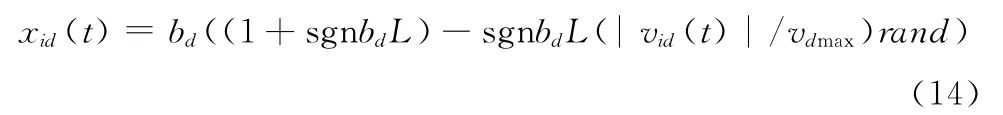
其中，sgn为符号函数，L∈［0，1］，ad表示粒子在第d 维的下限，bd表示粒子在第d 维的上限。边界缓冲墙根据粒子的实际飞行情况来处理越界粒子，动态设定粒子的缓冲边界，有效解决了传统处理方法所带来的问题。

3 算法具体流程

基于自适应混沌粒子群的聚类算法流程如下所示：

步骤1 初始化数据样本集中簇的数目和聚类中心。事先确定好模糊权重指数m，然后将簇的数目c进行初始化，并对聚类中心γj进行赋值，之后对粒子进行编码并初始化粒子的飞行速度vid（t）。

步骤2 计算隶属度、更新每个簇的聚类中心。利用式（4）计算每个粒子X［i］［k］［d］的隶属度uij，同时利用式（5）对每类的聚类中心γj进行更新。

步骤3 更新每个粒子的适应度目标值。利用式 （3）对每个粒子X［i］［k］［d］的适应度目标值进行计算，并根据目标值大小确定最优位置Pi和最优粒子Pg。

步骤4 更新所有粒子的位置和速度。使用式 （10）和式 （2）更新每个粒子的速度和位置，并同时启用边界缓冲墙，利用式 （13）和式 （14）将粒子的位置进行自适应调节。

步骤5 混沌搜索和扰动。利用式 （11）和式 （12）对粒子群进行混沌扰动优化，形成新的群体。

步骤6 结束条件判断。当算法结束条件满足时终止算法，并输出最优的簇中心矩阵。若不满足，则转到步骤2。

算法流程如图1所示。

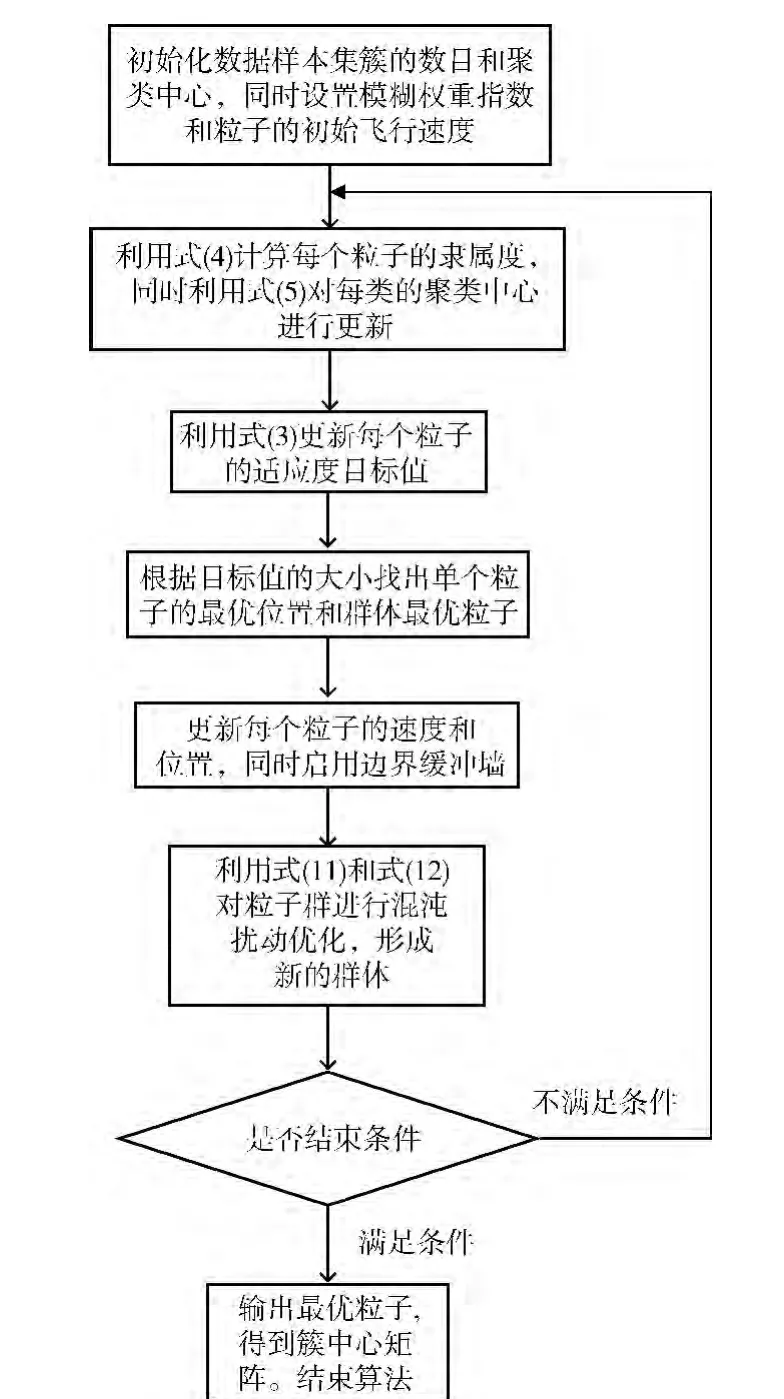
图1 算法流程

4 实验分析

为了测试本文所提算法的有效性，现进行实验仿真分析，并将本文所提算法的性能与其它几种常见的聚类算法进行比较。实验环境为：至强E5504 四核处理器，2G DDR3REG ECC内存，SATA2 500G 硬盘，英特尔5500服务器芯片组主板，操作系统为Microsoft Windows 2003 Server。

实验中参数设置如下：C－means算法中模糊权重指数m 为4，给定的类别数为3；PSO 算法中惯性权重w 为0.5，加速因子c1和c2为1.42；文献 ［12］算法中交叉因子和变异因子分别设置为pc＝0.9、pm ＝0.08，其中的惯性权重为0.75，加速因子为1.5；本文算法中权重系数σ＝3，协调因子k＝4，惯性权重w ＝0.5，混沌系统扰动系数u＝4，模糊权重指数m ＝3，缓冲墙的厚度L ＝0.3。

聚类实验的数据来源于在UCI机器学习库中的数据库，分别是Iris.dat、wine.dat、cmc.dat和zoo.dat这4个数据库。这4个数据库的简要描述见表1。

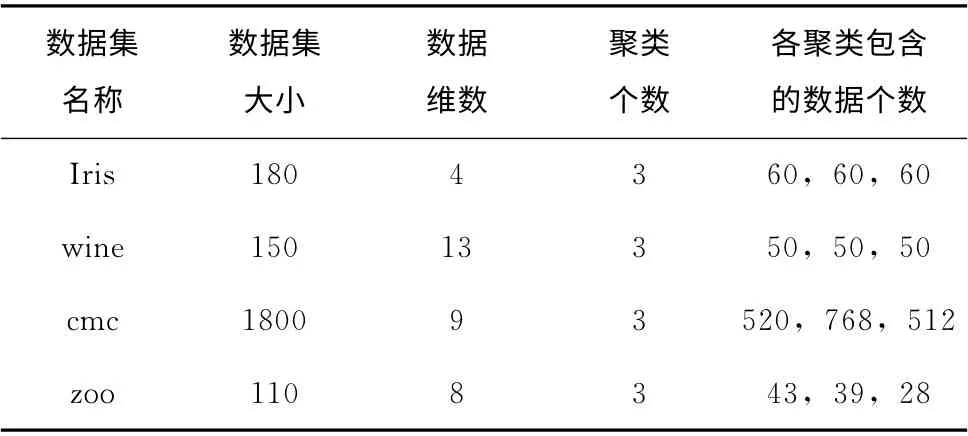
表1 实验数据描述

分别用C－means、PSO、文献 ［12］中的算法和本文所提算法对以上4个数据集进行聚类分析，为了避免其它外来随机因素的影响，将这4种算法各运行100 次，取平均值作为最后的对比结果，并对相应的结果进行统计分析。

从表2中可以看出，用C－means、PSO、文献 ［12］中的算法和本文所提算法对以上4个数据集进行聚类时，本文所提出的算法实现数据聚类的平均迭代次数最少，适应度目标值也最小。本文所提出的算法聚类Iris时，在第26次迭代时算法收敛，所得到的平均适应度值为86.6；Cmeans聚类Iris时，在第76次迭代时算法收敛，所得到的平均适应度值为97.3；标准PSO 聚类算法聚类Iris时，在第48次时算法收敛，所得到的平均适应度值为94.2；文献［12］算法聚类Iris时，在第32 次迭代时算法收敛，所得到的平均适应度值为89.4。本文所提出算法的聚类时间是C－means聚类算法的34.2%，是标准PSO 聚类算法的54.2%，是文献 ［12］算法的81.3%。同时，本文所提算法的聚类适应度目标值相对于其它3 种算法分别减少了11%、8.1%和3.1%。图2为各种算法聚类精度对比。

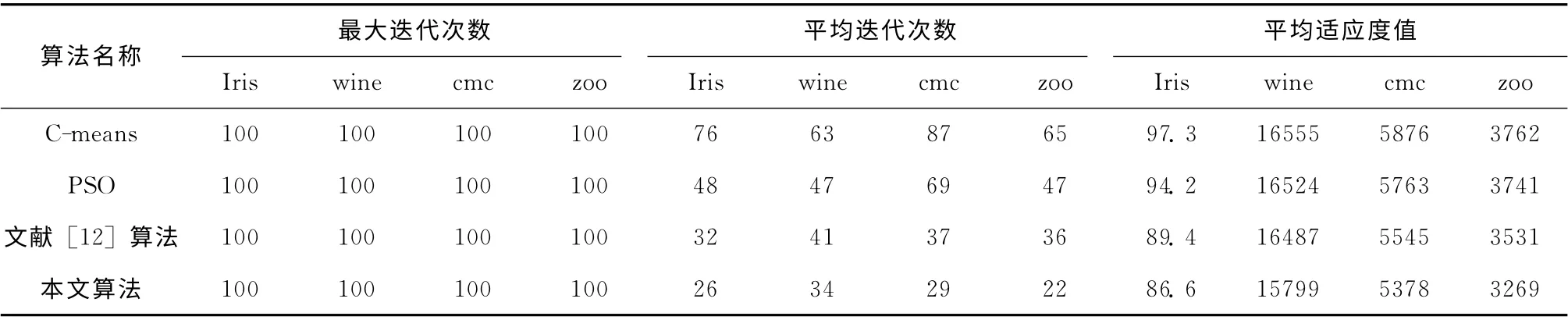
表2 各算法迭代次数及适应度值

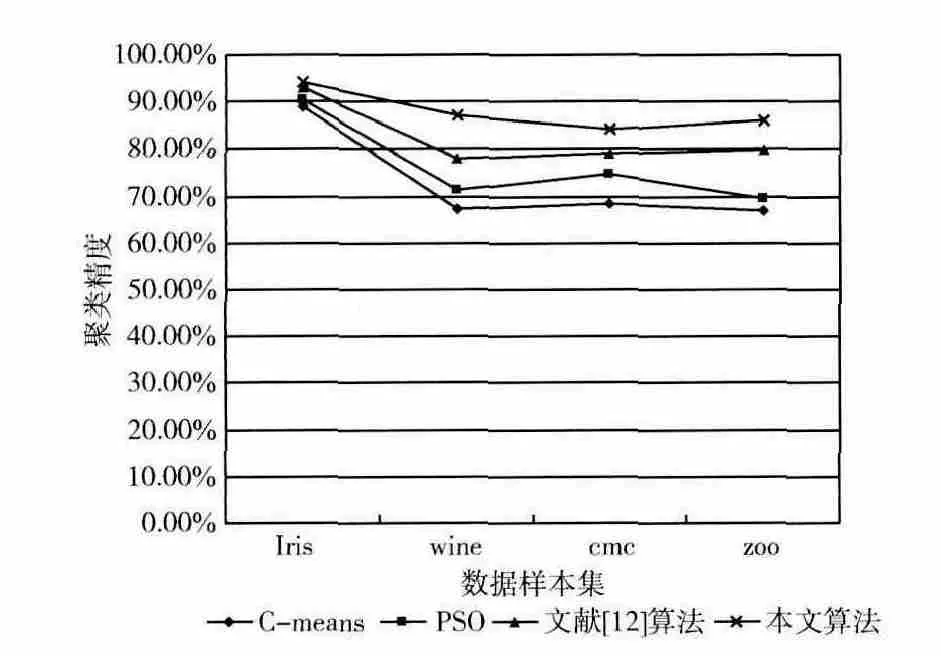
图2 各种算法聚类精度对比

从图2可以看出，在聚类Iris、wine、cmc和zoo这4种数据样本集时，本文所提算法的平均精度分别为89.1%、67.4%、68.3%和66.9%，要优于其它3种算法的聚类效果。本文所提算法在聚类zoo时，聚类精度为86.2%，相比于其它3种算法，其聚类精度分别提高了28.8%、23.9%和8.02%。

5 结束语

本文提出的基于自适应混沌粒子群的聚类算法将模糊c均值聚类和改进的PSO算法进行了有效的整合，避免了原模糊c均值聚类算法在处理高维数据集时表现出自适应性不强、易陷入局部极小值和聚类效果不理想等缺陷。通过选取UCI机器学习库中的4种数据样本集进行测试，测试结果表明，相比于C－means、PSO、文献 ［12］中的算法，本文所提出的算法在聚类精度、收敛速度及适应性上具有明显的优势。

［1］Hu Wei，Xu Fuyuan.An improved localization algorithm for performance improvement［J］.International Journal of Mobile Communications，2012，10 （4）：337－349.

［2］HU Wei，XU Fuyuan，MA Qingguo.Research of data stream clustering algorithms based on artificial immune principle ［J］.Computer Science，2012，39 （2）：195－197 （in Chinese）.［胡伟，徐福缘，马庆国.基于人工免疫原理的数据流聚类算法研究 ［J］.计算机科学，2012，39 （2）：195－197.］

［3］HU Wei，XU Fuyuan.Data clustering algorithm based on improved immune algorithm ［J］.Computer Engineering and Design，2012，33 （10）：3940－3944 （in Chinese）.［胡伟，徐福缘.基于改进免疫算法的数据聚类策略研究 ［J］.计算机工程与设计，2012，33 （10）：3940－3944.］

［4］Abdolreza Hatamlou，Salwani Abdullah，Hossein Nezamabadipour.A combined approach for clustering based on K－means and gravitational search algorithms ［J］.Swarm and Evolutionary Computation，2012，6 （10）：47－52.

［5］Liu Ruochen，Zhang Xiangrong.Immunodomaince based clonal selection clustering algorithm ［J］.Applied Soft Computing，2012，12 （1）：302－312.

［6］Mohammad Taherdangkoo，Mohammad Hadi Bagheri.A powerful hybrid clustering method based on modified stem cells and fuzzy C－means algorithms［J］.Engineering Applications of Artificial Intelligence，2013，26 （5）：1493－1502.

［7］Liu Jingwei，Xu Meizhi.Kernelized fuzzy attribute C－means clustering algorithm ［J］.Fuzzy Sets and Systems，2008，159（18）：2428－2445.

［8］Tsai Du－Ming，Lin Chung－Chan.Fuzzy C－means based clustering for linearly and nonlinearly separable data ［J］.Pattern Recognition，2011，44 （8）：1750－1760.

［9］Li Dan，Gu Hong，Zhang Liyong.A fuzzy c－means clustering algorithm based on nearest－neighbor intervals for incomplete data［J］.Expert Systems with Applications，2010，37 （10）：6942－6947.

［10］Tang Jun，Zhao Xiaojuan.An enhanced opposition－based particle swarm optimization ［C］//Global Congress on Intelligent Systems，2009：149－153.

［11］Wang Hui，Wu Zhijian，Liu Yong，et al.Particle swarm optimization with a novel multi－parent crossover operator［C］//The 4th International Conference on Natural Computation，2008：664－668.

［12］Kuo RJ，Syu YJ，Chen Zhen－Yao，et al.Integration of particle swarm optimization and genetic algorithm for dynamic clustering［J］.Information Sciences，2012，195 （15）：124－140.