基于支持向量机回归的城市PM2.5浓度预测

谢永华，张鸣敏，杨 乐，张恒德

（1.南京信息工程大学 计算机与软件学院，江苏 南京210044；2.南京信息工程大学江苏省网络监控中心，江苏 南京210044；3.中国气象局国家气象中心，北京100081）

0 引言

近年来对PM2.5［1，2］及相关污染物预测的研究主要有如下方法。Fuller等通过经验统计方法建立了月均PM2.5与其它污染物 （NOx，PM10）的线性关系，预测月均PM2.5浓度走向［3］；Chemel等用化学物质转化模型对PM2.5的历史数据进行建模，预测了年均PM2.5浓度值的变化［4］。上述经验模型需要大量观测数据，且具有明显的局域性，回归关系不能很好符合实际情况。Balachandran等利用贝叶斯算法分析了PM2.5的不同来源对其浓度的影响，并进行了中长期的预测实验［5］；Dong等利用隐半马尔科夫模型对PM2.5浓度进行了预测，具有24小时上的预报精度［6］。这些基于概率统计规律的建模方法对PM2.5的高维非线性系统的代表性不高。黄金杰等采用高斯扩散模型推算大气污染物间的变量关系，计算单一污染源对如PM2.5等污染物变化影响［7］；Domańska等利用混沌时间序列算法对短期PM10的浓度进行预测［8］；Voukantsis等利用多层感知的神经网络方法预测了两个城市的日均PM10变化规律［9］。值得注意的是，尽管神经网络等方法建模简单，但对于高维特征及非线性系统的预测问题则具有低泛化性、低鲁棒性以及过学习等问题。针对当前在PM2.5浓度预测方面存在的上述问题，本文提出了一种利用支持向量机回归 （support vector regression，SVR）方法进行PM2.5浓度预测的方法，该方法在较小规模的PM2.5监测数据样本上即具有较为理想的预测精度；同时，通过调节SVR 预测特征的时间跨度，可以在保证训练效率的情况有效提高SVR 方法的预测精度。本文展示的SVR 方法在中短期 （20小时）跨度上具有均一的预测精度，验证了其应用的广泛性与鲁棒性。

1 PM2.5浓度预测的原理

PM2.5浓度预测的主要目标是通过机器学习等方法得到PM2.5浓度与其它因素之间的回归关系，并就实际数据进行预测。PM2.5的预测主要可以概括为以下步骤：获取气象污染物 （PM2.5、PM10、SOx、NOx、O3等）浓度数据与气象数据 （气温、气压、湿度、风速风向等）；提取PM2.5浓度数据为模型因变量y （预测值），其它数据或其组合作为自变量x1，x2，...，xn（预测特征）；将数据集S 划分为训练Strain、验证Svalidate和测试集Stest；在训练集上通过机器学习训练生成模型，得到回归关系y＝f（x1，x2，...xi，...，xn）；通过比较不同模型参数在验证集上的预测量与实际数据y 的误差 （均方根误差MSE）大小选取最佳的参数及模型，最后在测试集上测试最优模型的预测MSE大小。流程如图1所示。

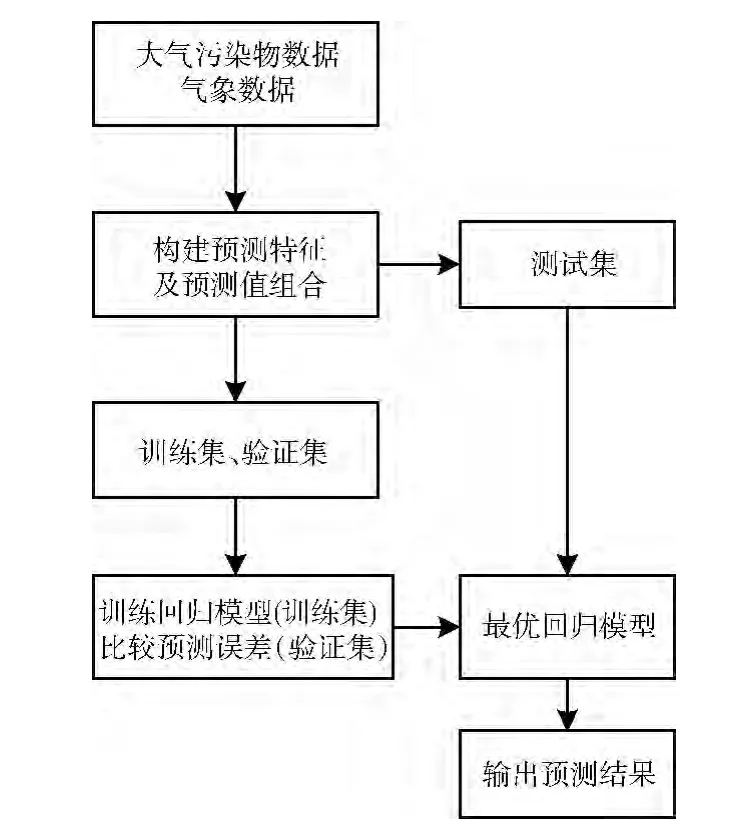
图1 PM2.5浓度预测流程

PM2.5浓度预测的重点提高预测模型的泛化性、鲁棒性和准确性。其难点主要体现在以下几个方面：

（1）合适的机器学习方法的选择。引言中方法存在着数据需求量大、局域性强、预测精度低、过学习等问题。

（2）降低不确定性。由于PM2.5雾霾体系存在相当大的随机性，仅使用单一时间的数据进行模型训练存在高不确定性，影响模型的精度。

（3）训练效率。机器学习中特征维度提高对模型的精度提高有帮助，但过度增加特征维度会显著增加训练时间。

针对PM2.5浓度预测中存在的上述难点，本文采用时序SVR 方法来进行建模。SVR 方法相对于其它学习方法，例如NN等，对高维及非线性问题具有很好的适应性，且所需数据量更小，适合我国目前PM2.5观测数据较少的现状。同时，利用时间序列的数据组合作为预测特征，减少了因系统自身引起的不确定性。最后，通过综合比较训练时间与预测精度，得到最优参数，确保了模型预测精度与训练效率。

2 研究方法

2.1 SVR 方法预测PM2.5浓度

2.1.1 SVR 理论概要

支持向量回归是一种基于惩罚学习的回归方法［10］。本节简要介绍了SVR 的基本原理。SVR 的总体目标是得到输入x 和结果y 之间的回归关系f（x），可以描述为一个近似线性回归的问题

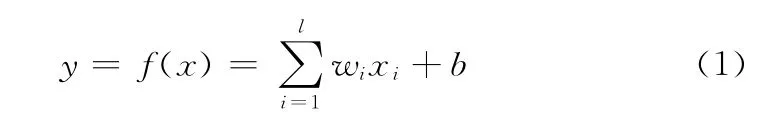
其中，回归系数w 和b 通过最优化方法获得。引入惩罚函数L来对预测值与实际值偏差大于阈值ε时的情况进行惩罚。其表达式为

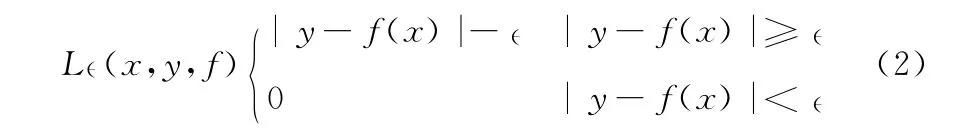
SVR 的优化问题的本质是解回归函数平面的宽度 （1／2）最小的问题。在存在误差的情况下，引入了松弛变量ξ－，ξ＋，来分别表示未超出和超出ε惩罚区间的情况。并结合参数C 来构成最终的风险函数R。SVR 问题的目标即转化为解在存在误差情况下的风险函数R 的最小化问题

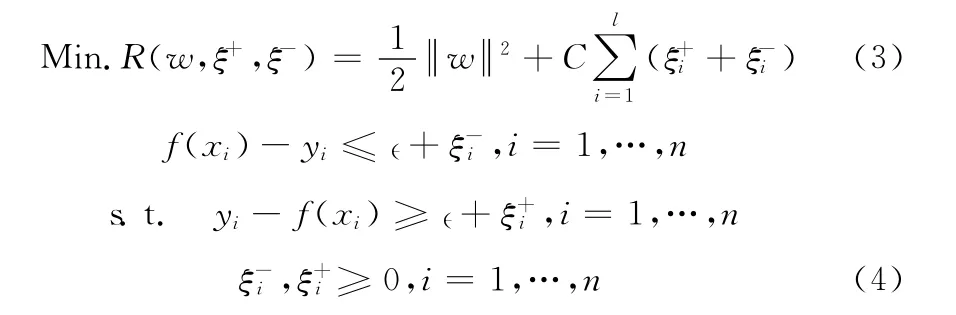
该优化问题是一个约束二次规划问题，可以通过引入Lagrange乘子，，将其转化为以下二次形式的问题

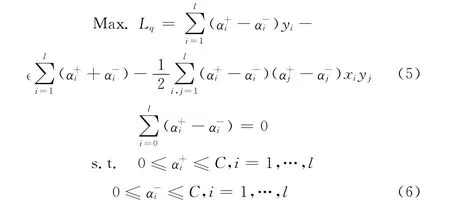
因此最初的回归目标可以表示成

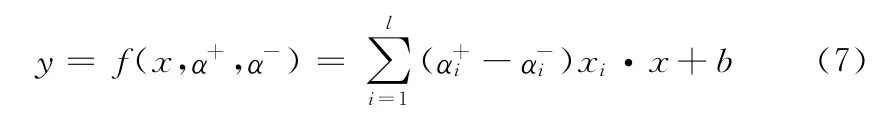
为了解决非线性回归问题，引入了内核映射方法，使用转换函数Φ将变量x 映射到高维非线性空间，并通过引入核函数K，K（xi，xj）＝Kxj＝Φ（xi）＊Φ（xj）来避免在同一特征空间的内积Φ（xi）＊Φ（xj）的计算，最后得到非线性回归表达式的最终形式为

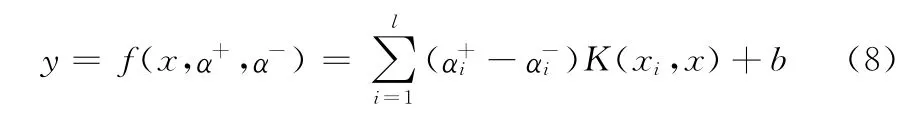
所有参数满足ξ－i ，ξ＋i ＝0的输入数据集xi则称为支持向量。支持向量即为落在ε－误差边界上的向量。支持向量代表了回归模型的特征，减少输入数据库中的无关向量。这使得SVR 方法相对其它机器学习方法，如NN，需要建模的样本数量更少。除了支持向量以外，其它样本数据的删减并不影响模型的训练效果，这一点在特征维度大于数据量时更为明显。

2.1.2 基于SVR 的时间序列预测

传统预测模型仅采用当前预测时间的预测因素作为输入值，忽略了污染物在时间序列上的相关性。对此，我们对SVR 方法中的数据进行了时序化处理。本文中所用参数（污染物浓度、气象条件）在某小时t可以表示为x（t）。这里我们使用当前时间 （t）前d 小时的数据作为SVR 模型的预测特征，预测值为p 小时后的PM2.5浓度值。回归问题目标可以表述为以下方程

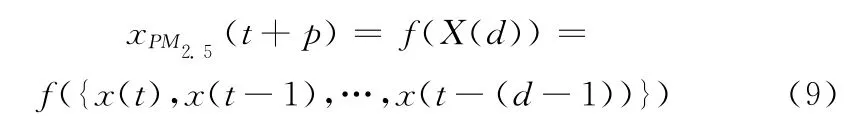
所选取数据的构成、预测特征与预测量的构成如图2所示。由于时间间隔的长度选取对模型的预测精度、模型训练时间都具有影响，因此最佳的时间间隔d 应是综合考虑预测精度与训练时间两方面的结果。针对时间序列预测建模的工作指出，最佳时间间隔d 与该时间序列的内在维度D 相关［11，12］。由于并没有通用的经验方法来确定最佳的d 值，这里我们通过比较模型性能和计算成本来获取最优解。

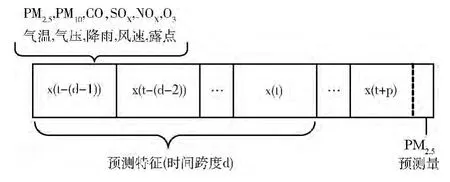
图2 SVR 模型数据结构

2.1.3 核函数及参数选取

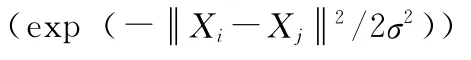
2.2 数据选取

本文中选取的5 个城市为北京、南京、武汉、成都和广州，分别代表了中国的各方位大城市的气象污染状况。空气污染数据抓取自中国环保部网站发布的实时信息，为2013年6月到12月的每小时数据，包括PM2.5、PM10、NO2、CO、SO2、O3等污染物数据。同时选取了温度、气压、降雨量、风速和和露点温度作为输入的气象参数。对数据进行了 ［0－1］归一化以提高SVR 模型泛化性。

2.3 程序方法与平台

本文中SVR 方法实验平台为OS X 10.9，2.4 GHz CPU，应用libSVM 程序库进行SVR 训练。其中，SVR的优化方法采用了序贯最小优化方法 （sequential minimal optimization，SMO）。SVR 参数的搜索算法使用C＋＋编写，使用了网格搜索算法。其它方法采用对应文献中的算法。

3 结果与讨论

3.1 各城市PM2.5状况的基本分析

所选的5个城市从2013年6月到12月的PM2.5浓度如图3所示，从图中我们可以看出，PM2.5在不同城市的变化趋势各不相同，广州平均浓度最低，为48.2μg／m3，其它4个城市的每小时平均浓度在70～85μg／m3之间，可见PM2.5浓度的差异与地理位置有着密切关系。在本文实验所选取的5 个城市中，广州位于亚热带季风气候地区，受海洋的影响比其它内陆城市大。成都位于四川盆地，相较于其它城市其空气循环受阻较为严重，影响到污染物浓度。除北京之外，其它几个城市受季节性影响较大，夏季的PM2.5浓度明显低于冬季。北京的PM2.5浓度变化与季节的相关性较低，这与其城市污染物来源复杂及工业水平有关。

尽管这5个城市的每小时平均PM2.5的浓度不超过80 μg／m3，但高PM2.5浓度的数据使得其数据波动较大。所有城市的具体统计数据如表1所示。从PM2.5的浓度的频率和分布可以得知，国内大部分城市的PM2.5浓度都超过了GB3905－2012标准所规定的指标 （见表2）。在这种高污染的情况下，显然适用于其它国家的统计学模型和化学传输模型都不适合我国的国情。此外，PM2.5的浓度受地理位置的影响较为明显，很难建立一个具有普适性的模型。机器学习方法，尤其是SVR 方法，可以分别针对不同城市的情况进行训练，具有很强的自适应性，有利于PM2.5浓度预测模型的建立。

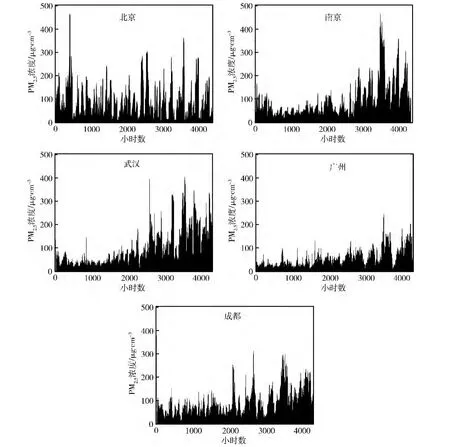
图3 所选城市从2013年6月至12月的PM2.5浓度变化 （起始点为2013年6月12日16点）

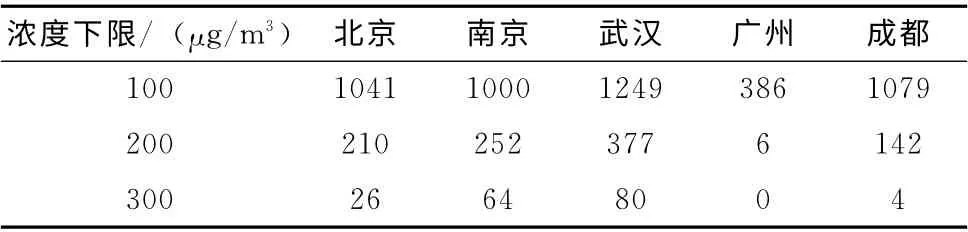
表1 各城市PM2.5浓度频率统计

表2 GB3095－2012对于大气颗粒物的监控标准

3.2 SVR 模型的预测结果

3.2.1 参数选取

考虑到数据的连续性问题，我们选取6月到8月的连续数据作为研究对象，其中包括1200 个小时的数据。前1000个小时的数据作为训练集，进行5等分交叉验证，后200个小时的数据作为验证集。参数值搜索采用等步长网格搜索方法，搜索范围为2－5－213，指数步长每次增加1。通过上述方法，可以获得最优的C，ε，σ参数。

在预测特征的时间跨度d 选取上，分别比较了时间跨度为1～7小时的训练时间和模型较差验证的精度，如表3所示。采用数据为南京前1000小时的数据，首先通过交叉验证寻得3个最优参数C，ε，和σ，并改变时间跨度d 的数值，通过预测数据的MSE数值比较，以得到最适合预测模型的d 参数。

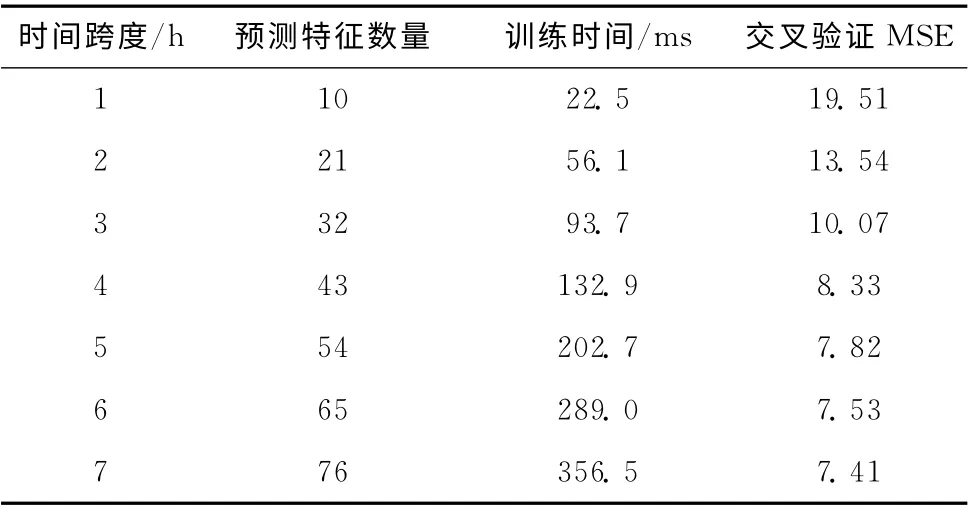
表3 不同时间跨度的预测特征的训练时间和精度比较

从表3中可以看出，在1～5小时上，随着预测特征时间跨度的增加，SVR 模型的预测精度有着显著的升高，说明了增长预测特征的时间跨度能够减少因PM2.5的不确定性引起的误差。当时间跨度增加到5 小时以上后，预测结果的MSE 值下降变缓，但模型的训练时间则大大增长，这是由于预测特征的数量的增加，在SVR方法这样的高时间复杂度算法下，将会大大增加其计算时间。综合考虑训练时间和SVR 模型精度，选取5 小时作为最优的预测特征时间跨度，能够保证预测精度及训练效率。

3.2.2 优化后模型的预测能力分析

5个城市的PM2.5浓度预测效果如图4与表4所示，其中所选的时间跨度均为5小时，预测值为预测特征后1小时的PM2.5浓度。可以看出，该时间跨度上每个城市的污染物均能得到很好的预测效果，相对误差基本小于10%，可以达到实际短期预测的效果。该方法对不同城市的PM2.5浓度预测均具有普适性，而并非传统经验模型或化学迁移模型很强的局域性。

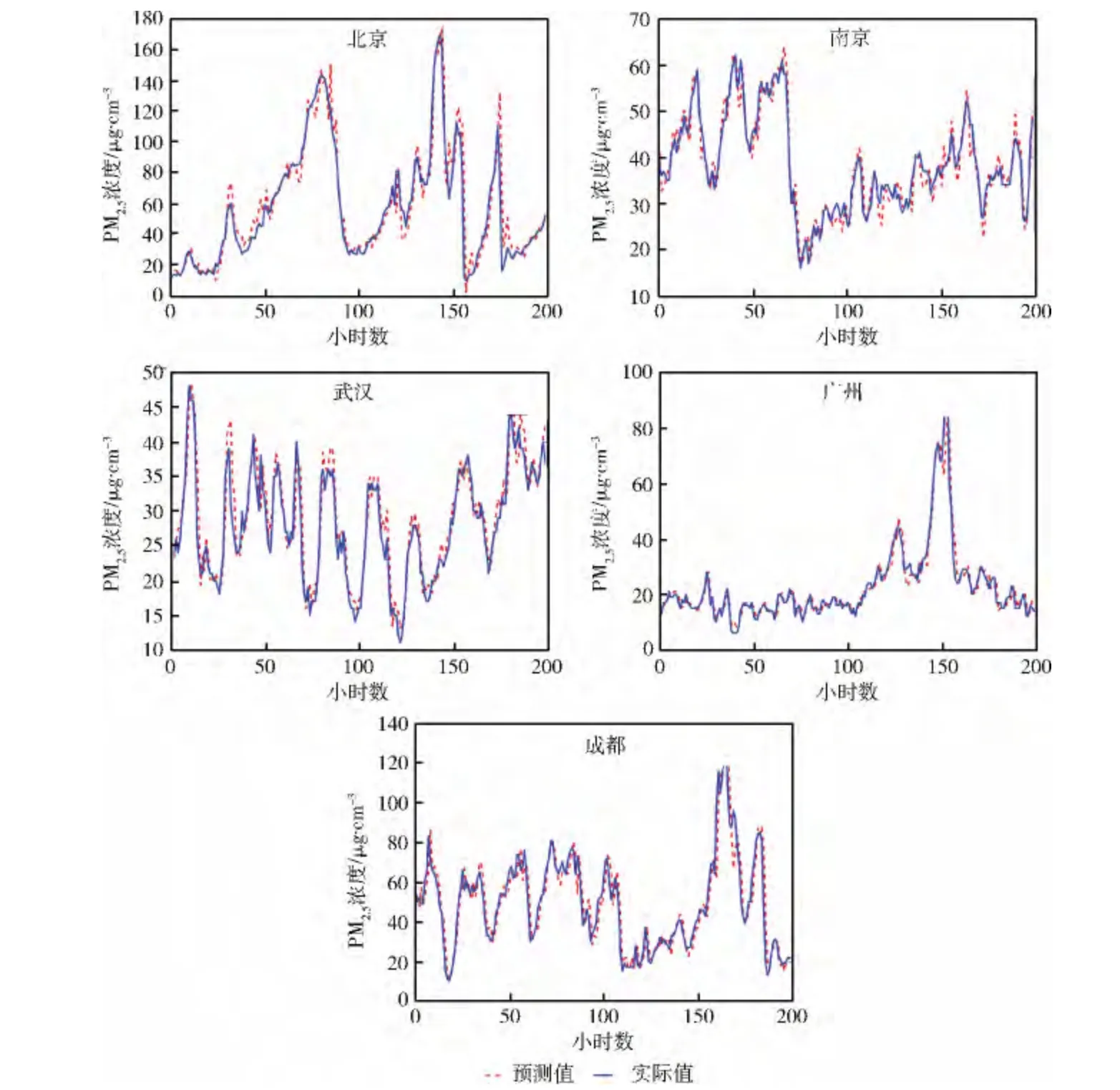
图4 训练集跨度为5小时的SVR 模型在各城市数据上的预测表现

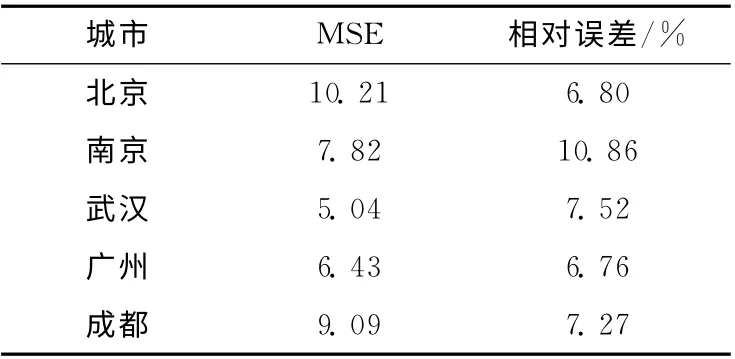
表4 各城市的PM2.5预测结果

3.2.3 预测结果的可信性

针对SVR 预测模型的预测结果可信性，我们同时对SVR方法在不同未来预测时间跨度上的预测效果进行了测试。我们选取了未来1到20个小时的时间跨度对南京市的数据进行了测试。如图5所示，所选取的时间跨度 （20h）上，SVR 预测结果的均方差都不超过20μg／m3，与此前实验结果的误差范围保持一致。这说明在当前预测参数的选取条件下，SVR 模型并未发生过学习问题，因此SVR 模型预测的结果具有可信性。此外在12小时附近MSE 值产生了极小值，这有可能与空气污染物的内在转化时间存在联系。

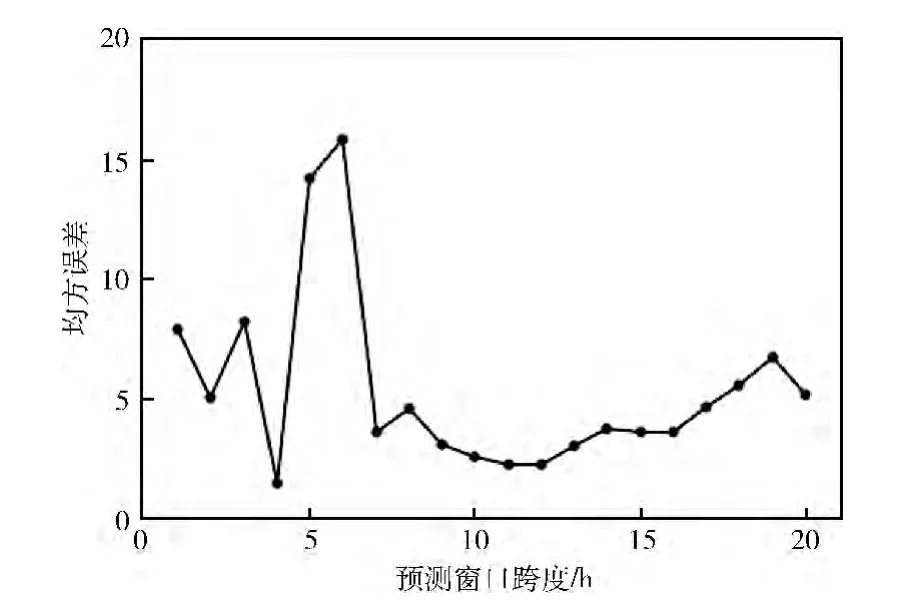
图5 不同时间跨度的预测误差比较

尽管预测MSE存在一定的波动，但均能够满足实际预测与污染物浓度分级的需要。由于本实验选用数据集规模不大，可以想见，如果有长期观测的数据积累，SVR模型预测的效果将会有进一步的提高。此外，我们就这种SVR 训练方法与其它文章中报道的用于大气污染物的其它机器学习方法（NN［9］、HSMM［6］）等进行比较，比较了5城市使用最优参数在前1000小时的平均训练时间与预测精度（见表5）。

表5 与其它方法的实验结果比较

结果表明，SVR 方法的预测误差率远低于其它方法，说明了其在处理高维非线性系统的适应性。SVR 方法的训练时间长于其它方法。由于SVR 方法为约束二次规划优化问题，通常需要使用内点算法等，相对于NN 方法等使用的梯度下降方法复杂度更高。尽管使用了SMO 优化，但SVR 方法在特征维度较高的情况下仍有更长的训练时间。后续可以考虑采用主成分分析 （PCA）等方法来选取有效特征，降低特征维度，减少训练时间。考虑到预测精确性的前提于，SVR 方法仍满足实际应用的需求。综上所述，本文使用的方法具有可行性与有效性。

4 结束语

PM2.5浓度预测是我国当前大气污染治理方面的重要问题，对实际应用具有重要意义。本文应用了支持向量机回归 （SVR）方法对我国5个城市的PM2.5浓度进行了建模与预测。利用各大气污染物浓度数据与气象数据因素训练模型，并通过调节预测特征时间间隔确保模型训练的效率与准确性。实验结果表明，相比其它机器学习方法，SVR 方法在所选城市的数据上均具有很高的预测精度，在中短期的预测应用上有着较好的表现，体现了其可行性与有效性。

［1］Fann N，Lamson A D，Anenberg SC，et al.Estimating the national public health burden associated with exposure to ambient PM2.5and ozone［J］.Risk Analysis，2012，32 （1）：81－95.

［2］MA H，SHEN H，LIANG Z，et al.Passengers’exposure to PM2.5，PM10，and CO2in typical underground subway platforms in shanghai［M］／／Proceedings of the 8th International Symposium on Heating，Ventilation and Air Conditioning.Berlin：Springer Berlin Heidelberg，2014：237－245.

［3］Franck U，Odeh S，Wiedensohler A，et al.The effect of particle size on cardiovascular disorders－The smaller the worse［J］.Science of the Total Environment，2011，409 （20）：4217－4221.

［4］Chemel C，Fisher BEA，Kong X，et al.Application of chemical transport model CMAQ to policy decisions regarding PM2.5in the UK ［J］.Atmospheric Environment，2014，82：410－417.

［5］Balachandran S，Chang HH，Pachon JE，et al.Bayesianbased ensemble source apportionment of PM2.5［J］.Environmental Science ＆Technology，2013，47 （23）：13511－13518.

［6］DONG M，YANG D，KUANG Y，et al.PM2.5concentration prediction using hidden semi－Markov model－based times series data mining ［J］.Expert Systems with Applications，2009，36（5）：9046－9055.

［7］HUANG Jinjie，YANG Guihua， MA Junchi.Evaluation model of air pollution based on gauss model ［J］.Computer Simulation，2011，28 （2）：101－104 （in Chinese）. ［黄金杰，杨桂花，马骏驰.基于高斯的大气污染评价模型 ［J］.计算机仿真，2011，28 （2）：101－104.］

［8］Domańska D，Wojtylak M.Application of fuzzy time series models for forecasting pollution concentrations ［J］.Expert Systems with Applications，2012，39 （9）：7673－7679.

［9］Voukantsis D，Karatzas K，Kukkonen J，et al.Intercomparison of air quality data using principal component analysis，and forecasting of PM10and PM2.5concentrations using artificial neural networks，in Thessaloniki and Helsinki［J］.Science of the Total Environment，2011，409 （7）：1266－1276.

［10］Ben－hur A，Weston J.A user’s guide to support vector machines［M］／／Data Mining Techniques for the Life Sciences.Humana Press，2010：223－239.

［11］Mellit A，Pavan A M，Benghanem M.Least squares support vector machine for short－term prediction of meteorological time series［J］.Theoretical and Applied Climatology，2013，111（1－2）：297－307.

［12］CHEN Rong，LIANG Changyong，XIE Fuwei，Application of nonlinear time series forecasting methods based on port vector regression ［J］.Journal of Hefei University of Technology，2013，36 （3）：369－374 （in Chinese）. ［陈荣，梁昌勇，谢福伟.基于SVR的非线性时间序列预测方法应用综述 ［J］.合肥工业大学学报：自然科学版，2013，36 （3）：369－374.］