高效自适应可验证抗篡改秘密共享方案

李瑞林，陈够喜，武雪芹

（中北大学 计算机与控制工程学院，山西 太原030051）

0 引 言

在现有的秘密共享方案中，有的方法只需保护一个子秘密就可以实现多个秘密的共享，称为多重秘密共享［1－3］，但在这种方法中一次秘密共享过程只能共享一个秘密。多秘密共享方案［4，5］解决了多重秘密共享方案的缺陷，在一次秘密共享过程中可以共享多个秘密。可验证秘密共享方案［6，7］可验证参与秘密共享的成员所拥有的子秘密的正确性，有效地避免不诚实参与者的欺诈行为。文献 ［6］基于传统的载体图像分块的思想，提出了可验证秘密共享方案，担此方案有着明显的缺陷，认证性能差，隐写图像失真度高。随后，研究者们提出了一些改进方法，如文献 ［7］提出了一种改进的高效可验证秘密共享方案，通过采用像素优化调整 （OPAP）来提高隐写图像的质量，但此方案仍存在认证值计算复杂度高、隐写图像质量有待提高等诸多问题。

针对上述不足，本文提出了一种高效可验证抗攻击抗篡改秘密共享方案，在本方案中运用Huffman编码缩小秘密图像的大小，即减少嵌入载体图像中信息量，提高隐写图像的质量，同时降低认证值计算的复杂度。重新定义了多项式输入值的计算，增强秘密图像像素点的关联性，防止不诚实参与者对图像的恶意篡改，增强隐写图像的安全性。

1 相关工作

1.1 基础理论模型

秘密图像S为灰度图像，大小为m×m，其中每个秘密像素si是单整型值，si∈S，由n个参与者共享。由n个参与者P（j）＝ ｛P（1），P（2），…，P（n）｝随机选择对应的n个载体图像为I（j）＝｛i（1），i（2），…，i（n）｝，I（j）的大小为2 m×2 m。一般选择，秘密图像S的大小为256×256，载体图像I（j）的大小为512×512，载体图像I（j）被划分为互不重叠的2×2块 （用来表示），其中1≤i≤m×m，1≤j≤n。每个块，，…，中的4个像素用Xi，Wi，Vi，Ui来表示，xi，wi，vi，ui分别表示其二进制值。如图1所示。

图1 2×2块的4像素表示

1.2 文献 ［7］的相关算法

1.2.1 认证比特的计算与嵌入

Wu等选择带子秘钥K3的哈希函数HK3（.）来计算4认证比特pi4，pi3，pi2，pi1。计算公式如下

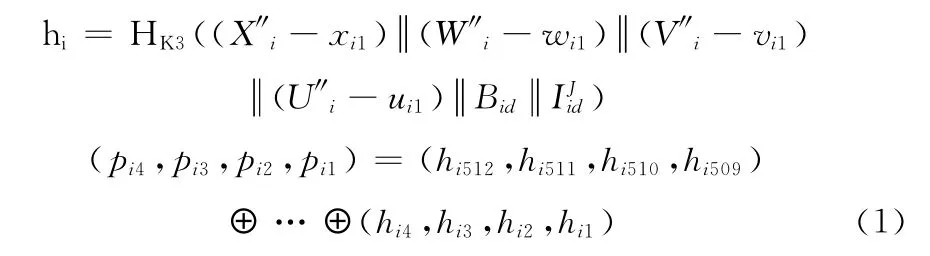
其中，（X″i－xi1），（W″－wi1），（V″－vi1），（U″－ui1）分别指 （xi8xi7xi6xi5xi4Fi8Fi7）， （wi8wi7wi6wi5wi4Fi6Fi5），（vi8vi7vi6vi5vi4Fi4Fi3）， （ui8ui7ui6ui5ui4Fi2Fi1）。Bid为块索引，Bid∈ ［1，m×m］，为参与者的私钥，HK（.）是RFC2104－HMAC标准哈希函数［8］。

1.2.2 OPAP像素优化

在方案的最后，通过OPAP 调整载体图像的像素值，降低隐写图像的失真度。设pi为载体图像第i个像素点的原始像素值，p′为嵌入了共享值和认证值后的载体像素值，运用了OPAP后的像素值为p″。计算公式如下

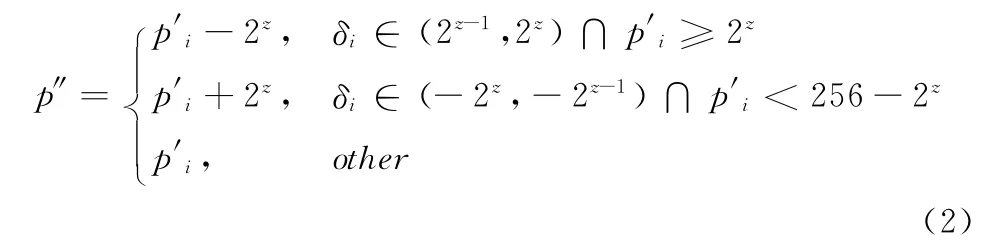
其中，δi＝p′i－pi；z为每个像素点嵌入的二进制位数。

2 自适应可验证秘密共享方案

2.1 方案内容

2.1.1 差分霍夫曼编码

将秘密图像S转化为差分图像DIF，再对DIF 按霍夫曼编码方式进行无损压缩产生影子图像S′。S′＝ ｛s′i｝＝｛s′1，s′2，…，s′t｝，i∈ ［1，t］。差分公式如下

2.1.2 秘密共享的计算

通过插值多项式计算秘密共享如下所示

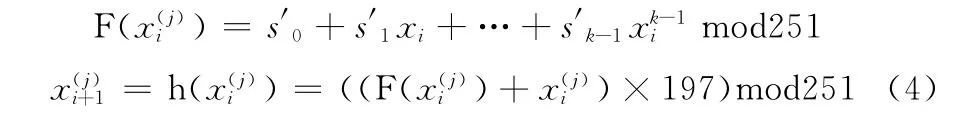
其中，s′0，s′1，…，s′k－1是从影子图像S′中选取的k个像素点。取＝ ｛1，2，…，n｝为载体图像的ID 号。作为多项式的输入，，，…，｝＝。而从x2开始，将秘密图像S中k个像素的共享F（），作为下一个多项式输入x的输入。显然，xi≠xj，完全满足插值多项式的要求。

2.1.3 秘密共享的嵌入位置

由于产生的影子图像S′小于原始秘密图像S，打破了基础模型中一个4像素块B（j）i处理一个秘密像素点的情况，所以需要确定S′中每个像素点si′在载体图像I（j）中的嵌入块位置。因此，本方案通过式 （5）来确定每个像素si′在载体图像I（j）中的随机嵌入位置

2.1.4 认证比特的计算

4比特哈希认证值pi4，pi3，pi2，pi1的计算公式如下

其中，（Fi8Fi7），（Fi6Fi5），（Fi4Fi3），（Fi2Fi1）是指嵌入的秘密共享信息。Bid为块索引，）为隐写图像ID 号，HK（.）是RFC2104－HMAC标准哈希函数［8］。

图2 嵌入共享值和认证值的4像素块B′（j）i

2.1.5 像素优化

在整个方案过程中，由于都是对要嵌入的秘密信息（即影子图像的每个像素点）做处理，所以在方案的最后，也只需要对嵌入了信息的载体图像像素点OPAP 来提高隐写图像质量。

2.2 秘密图像共享和恢复算法

2.2.1 嵌入算法

输入：一幅秘密图像S＝ ｛s1，s2，…，sm╳m｝，n个载体图像I（j）＝ ｛i（1），i（2），…，i（n）｝，和秘钥K3。

输出：n幅隐写图像I＊（j）＝ ｛i＊（1），i＊（2），…，i＊（n）｝。

（1）将n个载体图像I（j），分割为m×m 个互不重叠的2×2块。（1≤i≤m×m，1≤j≤n）；

（2）通过式 （3）将秘密图像S转换为差分图像DIF＝｛difij｝，并且对差分图像DIF霍夫曼编码压缩，产生影子图像S′；

（5）初始值 为｛pi－1，4，pi－1，3，pi－1，2，pi－1，1｝＝｛0，0，0，0｝。除了第一块，对于每一块通过式 （6）计算前一块的认证值pi－1，4，pi－1，3，pi－1，2，pi－1，1；

（7）重复步骤 （3）到步骤 （6），直到影子图像S′的所有像素全部隐藏；然后计算每个隐写图像的最后一块的4比特认证值，并且嵌入隐写图像的第一块中，处理结束的每个隐写块用表示。此时构造阶段结束。

2.2.2 提取算法

输入：n幅隐写图像I＊（j）＝ ｛i＊（1），i＊（2），…，i＊（n）｝和秘钥K3。

输出：秘密图像S＝ ｛s1，s2，…，sm╳m｝。

（1）将n个隐写图像I＊（j），分割为m×m 个互不重叠的2×2块。

（4）使用LSB算法从k个隐写块中提取到的8位二进制位的共享值，代入式 （4）恢复秘密像素 ｛s′0，s′1，…，s′k－1｝；

（5）重复步骤 （2）到步骤 （6）直到恢复出影子图像S′的所有像素点；

（6）通过霍夫曼解码，得到差分图像DIF；

（7）通过差分图像的逆过程恢复真正的秘密图像S。

3 方案分析

3.1 理论分析

3.1.1 安全性分析

秘密共享方案的安全性是指非授权的参与者子集无法重构秘密。

对影子图像S′利用Shamir门限方案的分发算法共享影子秘密 ｛s′i｝＝ ｛s′1，s′2，…，s′t｝，因此，基于Shamir秘密共享方案，任意少于k个参与者的集合都无法重构多项式F（）；

由于不同的影子像素s′i和s′i′，（1≤i≠i′≤t），对应的多项式F（xi′）≠F（xi），进而F（x（i＋1）′）≠F（x（i＋1）），因此参与者P（j＇）的秘密份额除了不能用于恢复F（）而且不能恢复F（），即影子图像S′以外的参与者的秘密份额对于恢复多项式F（）和F（）均不起作用，无法恢复出原始秘密图像S。

结合以上讨论可知，一个非授权的参与者P 子集不能计算出影子矩阵。因此，P 无法重构秘密S。以下命题成立。

命题：由方案参数之间的关系以及有参与者子集可以恢复伪秘密s′i对应的多项式F（x）＝＞可以求解矩阵S′＜＝＞恢复原始秘密矩阵S。

3.1.2 可验证性分析

在秘密验证阶段，参与者P（j）出示由其保管的隐写图像I＊（j），很容易从隐写块中提取，，，。通过式 （7）计算每一个隐写块的认证值pi4pi3pi2pi1，并与提取出的认证值进行比较；若＝，则判定第i份共享通过了验证，否则身份验证没有通过，隐写图像经过了非法篡改。

事实上，由多元变量单向散列函数 （6）的性质可知，无法伪造F，）， （≠，≠s′i），使得F（，）＝F（，）。因此，不诚实参与者的欺诈行为一定可以被检测出来。

本方案的优点在于只需验证参与者是否安全可信地保管了嵌入的影子秘密共享，而避免了无意地修改了非秘密比特位信息的参与者却不能通过身份验证，从而不能参与秘密的恢复。

3.1.3 失真度分析及对比

整个方案的总失真是由LSB 嵌入引起的失真Da，和OPAP像素优化Db两部分共同作用的结果。

由于OPAP操作并不会影响末z位［7］，所以OPAP 像素优化Db和LSB嵌入引起的失真Da是不相关的，则总失真可表示为D ＝Da－Db。则对于隐写图像I＊（j），总失真可以表示为D ＝∑qi＝0（Da（i）－Db（i）），其中，q是嵌入载体图像中秘密像素点的总个数。在Wu等方案中，q＝2m×2m，而本方案中，q＝t，t＜2m×2m。由表1可知，D″＜D′，所以相较于Wu等的方案，本方案明显降低了失真度。

表1 失真度对比

3.2 实验分析

选择大小为256×256的秘密图像，载体图像的大小为512×512，以 （2，n）门限方案为例。在相同的实验条件以及相同的参数设置之下，对本方案和Chang等［6］及Wu等［7］方案做了仿真实验。

3.2.1 实验效果图像对比分析

实验效果图列举如下，其中，图 （a）为原始秘密图像，图 （b）为压缩后图像的大小，图（c）为运用本方案提取出的秘密图像。图3 （c）、图4 （c）、图5 （c）分别是载体图像｛1，2｝｛1，3｝｛2，3｝｛2，4｝恢复出的秘密图像。

图3 载体图像 ｛1，2｝恢复得到秘密图像

图4 载体图像 ｛1，3｝恢复得秘密图像

图5 载体图像 ｛2，3｝恢复得秘密图像

从上述图3～图5多幅图像对比可看出，图 （a）和图（c）在人眼视觉上几乎不可区别的，由此说明所提方案得到的秘密图像具有较强的视觉质量。而图 （b）的大小明显小于图 （a）的大小，也可说明在所提方案中，需要嵌入载体图像的信息量显著小于Chang 等［6］和Wu 等［7］的方 ，及所提方案对载体图像的像素修改量小于Chang 等［6］和Wu等［7］的方案。

3.2.2 载体图像bit修改量对比分析

从图6和图7可以直观地看出，对比Chang等［6］和Wu等［7］的方案，在隐藏秘密共享信息及认证比特的过程中，不管载体图像和秘密图像怎么变化，本方案对载体图像的每个像素的修改量都是最小的，表明此方案在隐写图像中能得到最好的图像质量。

图6 随载体图像变化bit修改量变化的实验对比

图7 随载体图像与秘密图像变化bit修改量的变化

3.2.3 PSNR 值对比分析

峰值信噪比 （PSNR）是评价图像质量的客观标准。计算实验结果的PSNR 值，对比结果见表2。

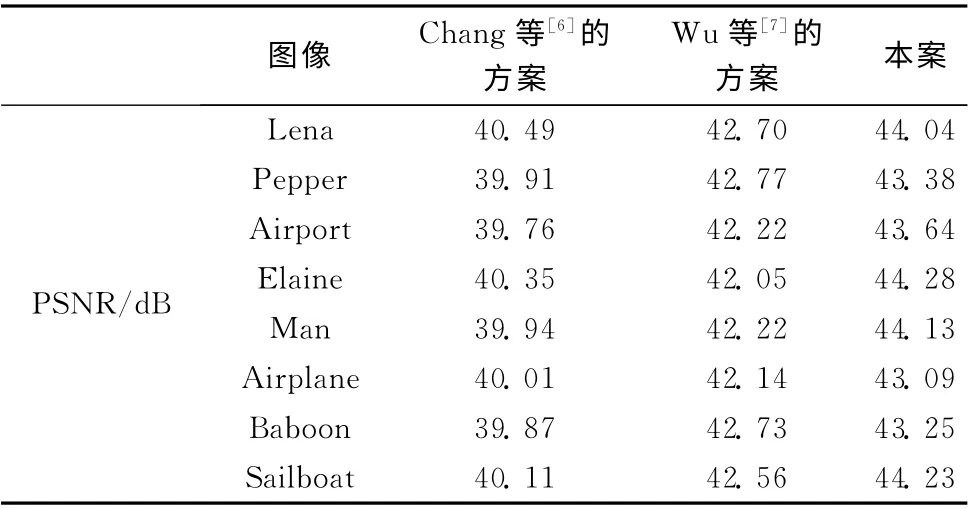
表2 各方案性能实验效果对比

表2中给出的8幅载体图像从其PSNR 值对比，直观明了地证明了，相比于Chang等［6］和Wu等［7］的方案，所提方案在实现秘密共享的过程中，在隐写图像中都能得到最好的图像质量。

3.2.4 DR 值对比分析

在认证方面，从图8 的DR 值对比中可看出，本方案的DR 值高于其它DR 值，也就是说，所提方案在认证性能方面要优于Chang等［6］和Wu等［7］的方案。

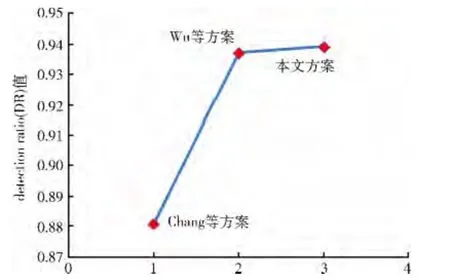
图8 3种方案的失真度 （DR）对比

最后，综合可得通过应用本方案可以得到一个高质量的隐写图像且具有高效可验证性。

4 结束语

本文提出了一个高效的自适应可验证秘密共享方案。通过对秘密图像差分哈夫曼编码处理，使得在之后嵌入及验证的过程中，都只需要对影子图像像素点进行插值多项式恢复及验证，节省了验证时间的同时增强了秘密图像的安全性。理论分析及实验对比表明，该方案可以得到一个高质量的隐写图像，具有低失真度、高可验证性及安全性。高可验证性增强了方案的防欺诈功能。而且操作简单、方便，具有很强的实用性，尤其适用于秘密信息少，高压缩比的灰度图像。但是，方案的效率还有待加强，是论文今后的一个考虑方向。

［1］WANG Xiang，PEI Qingqi，YAN Peimin，et al.A novel visual multi－secret sharing scheme based on folding－up operation［J］.Chinese of Journal Electronics，2013，22 （4）：795－798.

［2］LI Peng，MA Peijun，SU Xiaohong，et al.Multi－threshold image secret sharing scheme ［J］.Acta Electronica Sinica，2012，40 （3）：518－524 （in Chinese）.［李鹏，马培军，苏小红，等.多重门限的图像秘密共享方案 ［J］.电子学报，2012，40 （3）：518－524.］

［3］PANG Liaojun，PEI Qingqi，JIAO Licheng，et al.An identity （ID）－based threshold multi－secret sharing scheme［J］.Journal of Software，2008，19 （10）：2739－2745 （in Chinese）.［庞辽军，裴庆祺，焦李成，等.基于ID 的门限多重秘密共享方案 ［J］.软件学报，2008，19 （10）：2739－2745.］

［4］YU Jia，CHEN Yangkui，HAO Rong，et al.Publicly verifiable multi－secret sharing without trusted centers ［J］.Chinese Journal of Computers，2014，37 （5）：1030－1038 （in Chinese）.［于佳，陈养奎，郝蓉，等.无可信中心的可公开验证多秘密共享 ［J］.计算机学报，2014，37 （5）：1030－1038.］

［5］YU Bin，SHEN Gang，FU Zhengxin，et al.A lossless multisecret sharing visual cryptography scheme ［J］.Journal of Electronics ＆Information Technology，2012，34 （12）：2885－2890 （in Chinese）.［郁滨，沈刚，付正欣，等.一种无损多秘密分享视觉密码方案 ［J］.电子与信息学报，2012，34（12）：2885－2890.］

［6］Chang CC，Hsieh YP，Lin CH.Sharing secrets in stego images with authentication ［J］.Pattern Recognition，2008，41（10）：3130－3137.

［7］Wu Chia－Chun，Kao Shang－Juh，Hwang Min－Shiang.A high quality image sharing with steganography and adaptive authentication scheme［J］.Journal of Systems and Software，2011，84 （12）：2196－2207.

［8］Stallings W.Cryptography and network security：Principles and Practice［M］.5th ed.Prentice Hall，2010.

［9］Lee CF，Chen HL.A novel data hiding scheme based on modulus function ［J］.Journal of Systems and Software，2010，83（5）：832－843.

［10］Elshoura SM，Megherbi DB.A secure high capacity full－grayscale－level multi－image information hiding and secret image authentication scheme via Tchebichef moments［J］.Signal Processing－Image Communication，2013，28 （5）：531－552.

［11］Lee JD，Chiou YH，Guo JM.Information hiding based on block match coding for vector quantization－compressed images［J］.IEEE Systems Journal，2014，8 （3）：737－748.

［12］Nasrollah Pakniat，Mahnaz Noroozi，Ziba Eslami.Secret image sharing scheme with hierarchical threshold access structure［J］.Journal of Visual Communication and Image Representation，2014，25 （5）：1093－1101.

［13］Chen Chienchang，Wu Weijie.A secure Boolean－based multisecret image sharing scheme［J］.Journal of Systems ＆Software，2014，87 （92）：107－114.

［14］Abd El－Latif，Yan AA，Wang XH，et al.A new meaningful secret sharing scheme based on random grids，error diffusion and chaotic encryption ［J］.Optics ＆ Laser Technology，2013，54 （30）：389－400.

［15］Castiglione A，Santis De，Soriente AC.Security and privacy issues in the portable document format［J］.Journal of Systems and Software，2010，83 （10）：1813－1822.