基于神经网络实现分布评估的多目标差分算法

李艳玮，郑伟勇

（河南工程学院 计算机学院，河南 郑州451191）

0 引 言

进化算法的优化机制与多目标问题的特性之间存在一定的偏差［1，2］，前者主要利用种群中个体之间的局部梯度信息以及随机扰动信息，缺乏全局性的导向；后者往往需要在解空间中获取宽广分布的优化曲面 （线），要求算法具有较强的全局探索能力［3］。分布估计算法是一种基于统计分析的新型优化算法，利用当前种群的取值来评估最优解集的全局分布特性，进而通过基于统计模型的采样过程产生新的个体，反过来又进一步更新采样模型，最终推动算法的迭代演进［4］，显现出了良好的全局寻优性能［5］，但却严重依赖于统计模型的准确性，由于种群中个体数量以及函数计算资源都是有限的，会使得分布估计的模型与真实结果存在偏差。为此，提出了一种基于神经网络实现分布评估的多目标差分进化算法 （MDE－ED－ASM），在流形空间中分区域建立不同的分布估计模型，采用基于神经网络的代理模型来增加分布估计的统计样本和保持样本的准确度。同时，设计了自适应参量来调整差分进化算法和分布估计算法的选择概率，利用高效的差分进化算法来引导种群的分布趋势。

1 相关描述

多目标优化问题是在解空间x∈S∈Rn（n为变量x 的维数）中同时求取函数向量F＝ ｛f1，f2，…，fm，m≥2｝的极值 （假设求取最小值）。由于函数之间存在相互制约的关系，因此不存在能同时达到各个函数极值的单一解，而是最终得到一些由Pareto占优概念确定的折中解集，称为Pareto占优解集。对于该解集中的任意一个解x＊ （称为Pareto占优解），不存在任何一个解变量x∈S 使得：fi（x）≤fi（x＊），i＝1，2，…，m，且至少在一个函数上满足fi（x）＜fi（x＊）。而折中解集内部的解表现为：若在一部分函数上取值优于其它解，则必然在另一部分函数上取值差于其它解。

进化算法、分布估计算法和代理模型在求解多目标问题中的作用如图1所示。

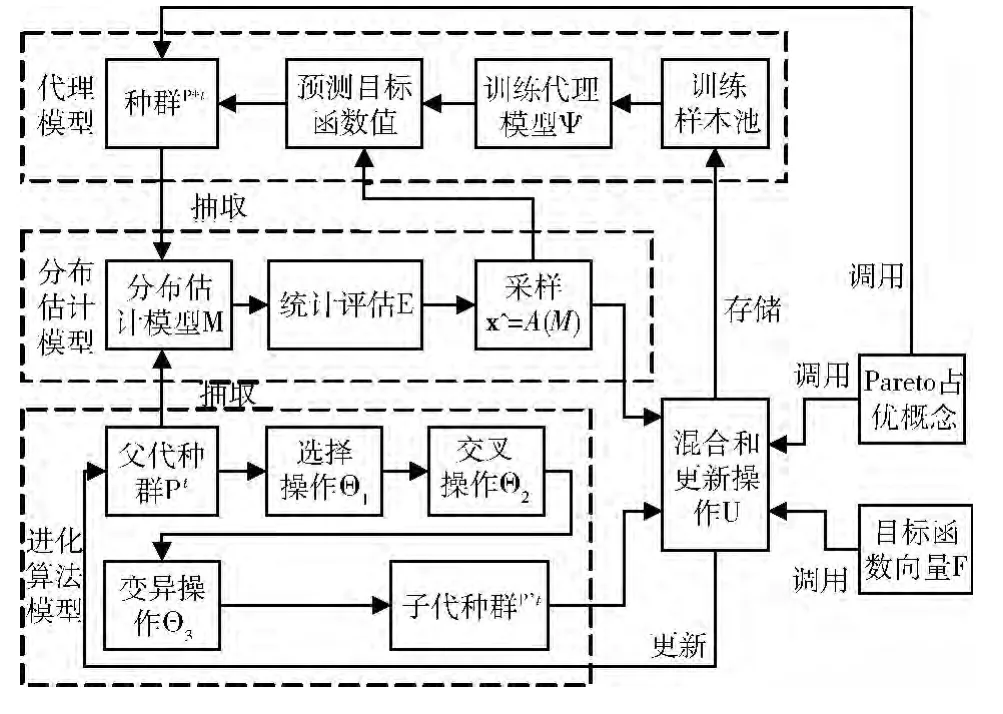
图1 相关概念在求解多目标问题中的作用

进化算法在每一次迭代过程中，将父代种群Pt＝ ｛xi，i＝1，2，…，p｝通过选择操作Θ1、交叉操作Θ2和变异操作Θ3得到子代种群P’t＝ ｛x～i，i＝1，2，…，p｜x～i＝Θ3（Θ2（Θ1（xi）））｝，再依据Pareto占优概念实现更新操作U，得到新的父代种群Pt＋1＝U （Pt，P’t），经过若干代后，种群中满足Pareto占优概念的个体即为最优解集。而分布估计算法则认为最优解集服从某一分布模型M（θ1，θ2，…，θl），并假设当前种群Pt中的部分或全部个体反映了最优解集的分布情况。其通过统计评估操作E 可以得到模型参数的估计值，，…，＝E（Pt），再基于这些估计值进行模型采样操作A，得到服从最优解集分布规律的新个体＝A（M（，，…，）），再用这些新个体依据Pareto占优概念更新种群，进而提升参数的估计值。如此螺旋上升，使得最终参数估计值趋近于真实值，采样所得解集也趋近于理论最优解集。代理模型鉴于当前有限的种群数量会影响参数估计值的精度，而增加个体数量会增多函数调用的资源，提出采用当前已知的若干最优解来建立变量与目标函数之间的映射关系F（x）＝Ψ（x），使得代理模型Ψ能够在一定精度下取代函数F 的调用，且计算速度快于F。代理模型所得解集P＊t与进化算法所得种群P’t混合得到更多的评估样本，提高了分布估计的精度。

2 算法设计

2.1 分布估计模型设计

依据Karush－Kuhn－Tucker条件，连续多目标优化问题对应的最优解集在解空间中是分段分布在多个流形上的［6］。因此，为了更好评估最优解集的分布形式，文中提出的算法MDE－ED－ASM 在建立分布估计模型M 时，先将待抽取的解集做处理：

（1）将所有个体在解变量空间下分成c类，其中每次聚类时c的取值由前一次所构建的代理模型数量确定，每个代理模型有一个类中心，解变量的类别归属原则为选择欧式距离最近的类中心；

（2）假设第k类的个体数量为nk，则记nk个个体的均值为ak，对其进行主成分分析，即按式 （1）求取其协方差矩阵Rk，再求取Rk的特征值和特征向量，j＝1，2，…，n，其中特征值满足λkj≥λk（j＋1），再根据式 （2）设定的累积贡献率η来确定主元的数量q。基于上述主成分分析所得参数，本文算法可得到每个类对应的观察窗口Φk和窗口的高斯噪声σk，而该类所在区域的最优解集即均匀分布在此观察窗口Φk中。具体而言，将第k类中所有个体按照式 （3）投影到前q个主元中，以确定观察窗口Φk的上界和下界。再考虑到类中个体未必能完全覆盖所处的流形区域，因此将上下界按照式 （4）做进一步的扩展，即得到最终的Φk。高斯噪声σk则代表了窗口的观察误差，其按照式（5）计算得到。可见，Φk和σk即为本文算法在统计评估操作E 中所求取的模型参数θ1，θ2，…，θl

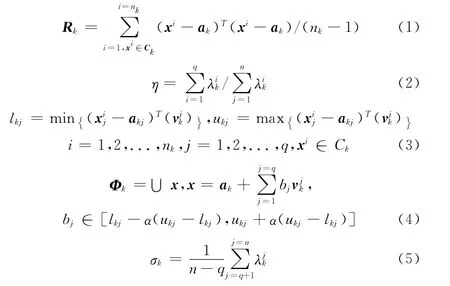
其中，Ck表示第k 类样本所在的类集合，α表示扩展系数，本文设定为10%。

在采样操作阶段，首先产生一个临时变量y，该变量的每一维均从观察窗口Φk对应维数的上下界之间随机生成。然后再生成一个变量ε，其每一维由均值为0，方差为σk的高斯函数生成。新生成的个体即为变量y 和ε的叠加，若在某一维上叠加的结果超出解空间的边界，则在解空间所确定的范围内随机生成该维的取值。本文设定对每个分布估计模型采样相同数量的样本，这样有助于个体总数较少的类也产生大量的新个体，从而加强了空间中稀疏区域解的密度。

2.2 代理模型设计

采用了多个神经网络模型分区域布置的架构。其原因不仅在于最优解集是分段分布在不同流形上的，并且从变量x到F 的函数映射形式也通常较为复杂，单一的神经网络模型是无法准确约近函数映射关系的［7］。设计的代理模型具有3个设计特点：①利用主成分分析方法将解变量映射到主元空间中，以减少神经网络的节点规模；②采用基于高斯核的径向基 （RBF）神经网络来提高代理模型的逼近效果；③在不同的类数取值下利用聚类算法划分出不同的区域，通过超体积指标测试不同类数下神经网络模型集的精度，得出最佳的区域划分数量。

假设构建c个神经网络模型，构建模型用的解集存入一个设定最大容量的训练样本池，记为TP，其元素的变量取值和目标函数值都是已知的。解集TP 的来源为分布估计算法和差分进化算法所产生子代中的Pareto占优个体。本文方法首先用K 均值算法将解集TP 划分为c 类，c∈［2，cmax］。由于每一类样本将用于构建一个代理模型，样本过少将无法有效完成模型的训练过程。因此当K 均值聚类结果中某一类的样本数量少于阈值δ时，则计算该类样本与其它各类中心的欧式距离，按照最近原则并入其余类中。再随机选取一个样本数量大于2δ的类，选择其中距离类中心最远的样本s1和距离s1最远的样本s2，将其余样本按照距离s1和s2的远近划分成两个新的类。对于每一个类的样本，采用与分布估计模型设计中类似的步骤进行主成分分析，得到相应的主元数量q和特征向量v’kj，j＝1，2，…，n，再将类中样本依照式 （6）投影到主元空间中，得到维数为q的投影向量z，再以此作为神经网络的输入节点个数

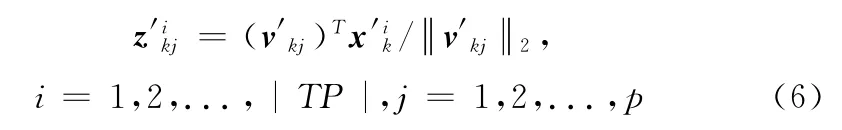
本文具体选择训练速度快，非线性映射能力强的RBF神经网络作为具体的代理模型。其输入节点数、隐含层节点数 （即径向基的个数）和输出节点数分别设置为q、2q和m。其余参数，包括各个径向基的方差、基函数中心以及隐含层与输出层之间的权重，均以最小化输出误差的平方和为目标函数，采用最速梯度法进行有监督学习来确定。

在所提算法中，类数c是分布估计模型和代理模型中的重要参数，其显著影响了算法关于最优解集所在分段流形空间的建模精度。因此，本文将类c从2 逐渐增加，在每种类数下进行聚类和神经网络训练，再从中选取最好训练结果对应的类数为最终确定的类数。又由于神经网络模型以最小化输出与真实函数值的误差为目标，不能很好顾及最优解集要全面均匀逼近最优曲面 （线）的准则，即可能出现曲面上某些小的区域精度高，其余大而样本少的区域精度低。因此，本文采用超体积指标作为评价神经网络集的训练结果好坏的标准。该指标通常用于全面评价多目标优化算法所得结果的质量［8，9］，如式 （7）所示

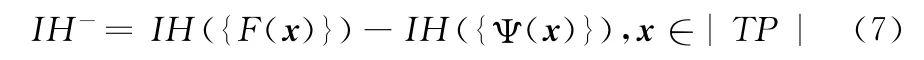
其中，IH （·）称为超体积测度，由文献 ［10］所述计算方法获得。其取值越小则说明解集的质量越好。在具体操作中，首先将类数为c时每一类的样本等分为两份，一份用于完成前述神经网络的训练；另一部分作为验证样本，利用得到的神经网络模型预测函数值Ψ（x），将Ψ（x）和F（x）代入式 （7）中进行计算，再将所有类的超体积指标值求和，求和值最小时对应的c值即为最佳聚类类数。

2.3 算法混合机制的设计

代理模型通过提供大量可靠样本来提升分布估计模型的性能，但客观上其预测值总是会与实际函数值存在差异，而差分进化算法则在现有优化解集上进行高效搜索以提供若干均匀分布且取值准确的样本，可加速实现分布估计模型的校准本文选用的差分算子为DE／current－to－rand／1［11］，其具有较好的探索能力，不易导致强收敛到单个极值，并且变异和交叉操作整合到同一公式中，形式简单，如式 （8）所示

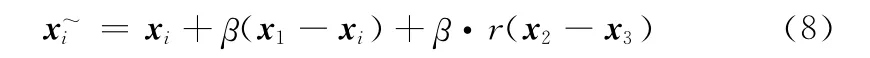
式中：β—— ［0，1］之间随机选取的参数，r——比例因子，本文设定为 ［0.05，，0.95］之间随机选取，xi、x1、x2和x3——随机选取的4个不同个体。

算法MDE－ED－ASM 中每个子代个体依概率ps选择由分布估计模型生成，或者由差分进化算法生成。概率ps在初始时取为0.5，此后随着分布估计模型的更新而根据式（9）自适应的变化

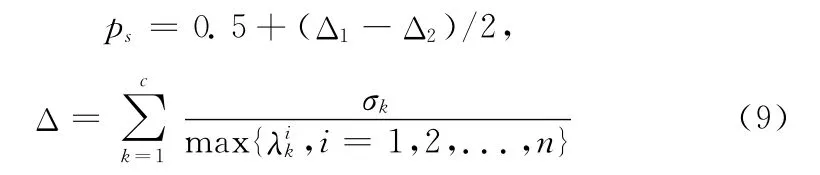
式中：Δ——当前各个流行区间上分布估计模型的整体噪声幅度，取值越大说明当前模型的分布估计精度受噪声的影响越大。而Δ1和Δ2分别表示了前一次的噪声幅度和当前的噪声幅度，（Δ1－Δ2）的取值大于零则说明分布估计模型的精度提升，更多的个体可以用分布估计模型来生成，以加强全局搜索能力，取值小于零则需要更多调用差分算子来纠正算法的优化方向。

2.4 算法流程

基于上述模型的阐述，算法MDE－ED－ASM 的运行流程可描述为：

步骤1 随机生成p 个个体，记为父代种群Pt，令代数t＝0，计算中每个个体的目标函数值，并按照Pareto占优概念选出Pareto占优解集，放入训练池TP中；

步骤2 当t＜ta时，按照差分进化算法的流程产生新个体并更新父代种群，同时将每代得到的Pareto占优解放入训练池TP 中，若TP 中已有的解相对于新放入解不再Pareto占优，则予以剔除，若TP中的解数量超出最大值，则按照Pareto占优和拥挤距离概念［12］予以约简；

步骤3 当t≥ta时，依照概率ps决定每个子代个体是由差分算子或分布估计模型生成，同时在每代的末尾更新训练池TP；

步骤4 当t＝ta时，利用父代种群构建分布估计模型，此时的类数c在 ［2，cmax］之间随机选取；

步骤5 当t＞ta且t除以ta的余数为0时，将训练池中的样本按照2.2节所述方法处理，构建神经网络模型集，并从已有分布估计模型中采样生成10p 个样本，用神经网络模型预测出相应的目标函数值Ψ（x），然后根据Ψ（x）选出其中的Pareto占优解，将这些解和父代种群Pt一并作为抽取样本，用于更新分布估计模型，此外，根据更新前后的噪声幅度Δ1和Δ2，对概率ps进行更新；

步骤6 当t＝tmax时，将父代中的Pareto占优解集作为最终优化结果输出。

3 验证与分析

为了验证所提模型的有效性，选择3 个二维问题及2个高维多目标优化问题作为测试对象，并选择经典多目标优化算法NSGA－II［13］和多目标分布估计算法RM－MEDA［6］作为对比算法。其中记二维问题记为F1、F2和F3，F1为2009年进化计算年会 （CEC2009）［13］上提出的多目标测试用例中的第一个测试函数，F2和F3分别与文献 ［6］中所使用的问题标号相对应，而高维优化问题F4和F5分别对应CEC2009上提出的多目标测试用例中的两个5维优化问题R2＿DTLZ2＿M5和R2＿DTLZ3＿M5。所提算法的相关参数设置如下所示：设置种群大小p 为100，训练池TP为500，参数ta为20，cmax为10，最大函数调用次数为50000次，即最大代数tmax为500代。所有算法均在达到最大函数调用次数时停止，每种算法独立运行25次，记录每次所得最优解集的逆广义距离指标IGD 和超体积指标IH－［14］，统计这25 次的指标均值作为评价算法性能的标准，取值越小说明算法的优化性能越好。3 种算法的测试结果见表1。

表1中加粗部分表示对应算法在该函数上的优化结果最好。可以发现，所提算法MDE－ED－ASM 除了在函数F3上的超体积指标略差于RM－MEDA 以外，其余的测试结果均好于其它算法；MDE－ED－ASM 和RM－MEDA 均采用分布估计的方法加强全局优化能力，获得的测试结果也表明算法性能好于无分布估计方法的NSGA－II；MDE－EDASM 在高维问题F4 和F5 上的测试结果明显好于RMMEDA，也表明所提算法在处理高维问题时未出现明显的性能衰退。

表1 3种算法的测试结果对比

与RM－MEDA 相比，算法MDE－ED－ASM 利用代理模型和差分进化来加强分布估计的性能。为了分析这两种措施的作用，设计了两个对比算法，第一种算法去除代理模型，只用差分进化和分布估计得到的子代个体来更新分布估计模型，记为MDE－ED，此时分布估计中的类数随机生成；第二种算法将差分进化算子替换为式 （10）中的普通算术交叉算子，记为MGA－ED－ASM

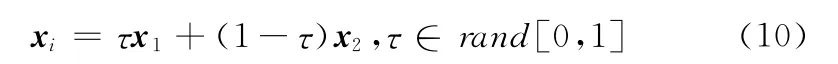
以测试问题F1和F4为研究对象，算法的对比结果见表2。

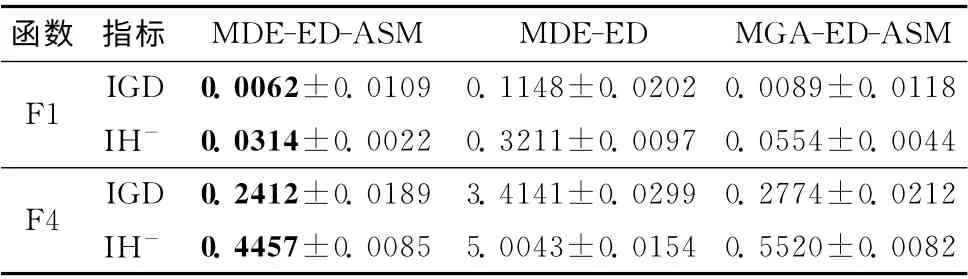
表2 代理模型和差分算子的性能分析

可见代理模型显著提升了所提算法的性能，而差分进化算子也使得算法有一定的提升。为了进一步说明二者的性能，本文记录了各个算法优化函数F1时，在进化过程中第100代到第5000代之间的一些取值变化情况。这些值包括算法在相应代数所得Pareto占优解集的IGD 值，代理模型所确定的最佳类数c，以及反映分布估计模型精度的噪声幅度值Δ，分别如图2～图4所示。

从图2结果显示MGA－ED－ASM 采用普通的交叉算子后，尽管最终也得到了较好的IGD 指标，但其相比于MDE－ED－ASM，花费了更多的函数调用次数才得到同等量级的优化结果，而MDE－ED的效果则更差，甚至无法得到较高量级的指标。

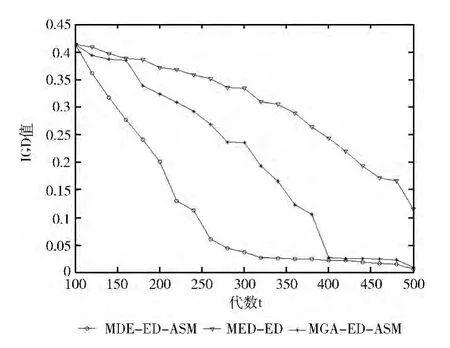
图2 代理模型和差分算子对IGD 值的影响

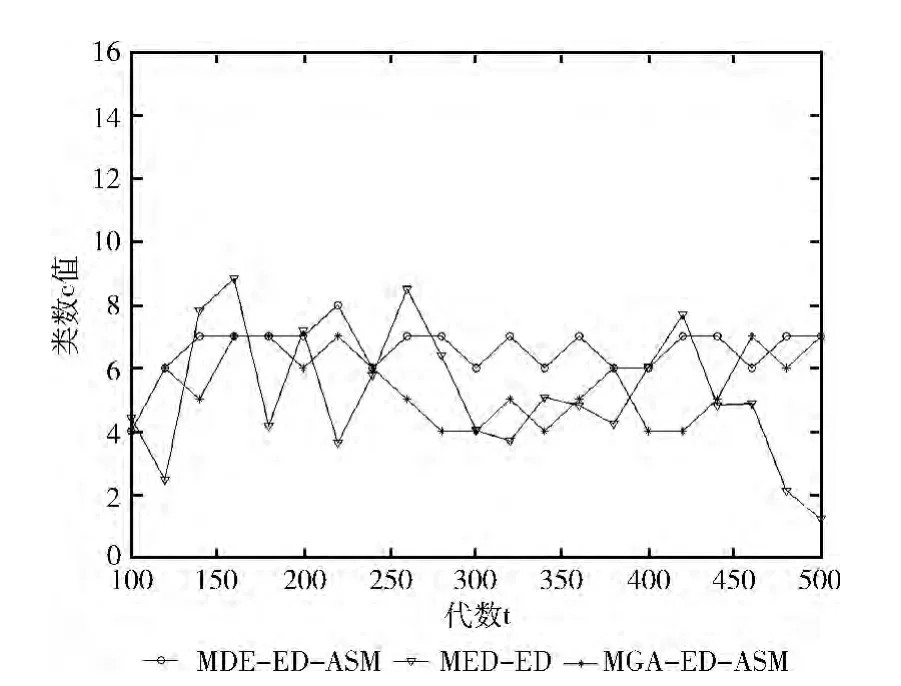
图3 代理模型和差分算子对类数c值的影响

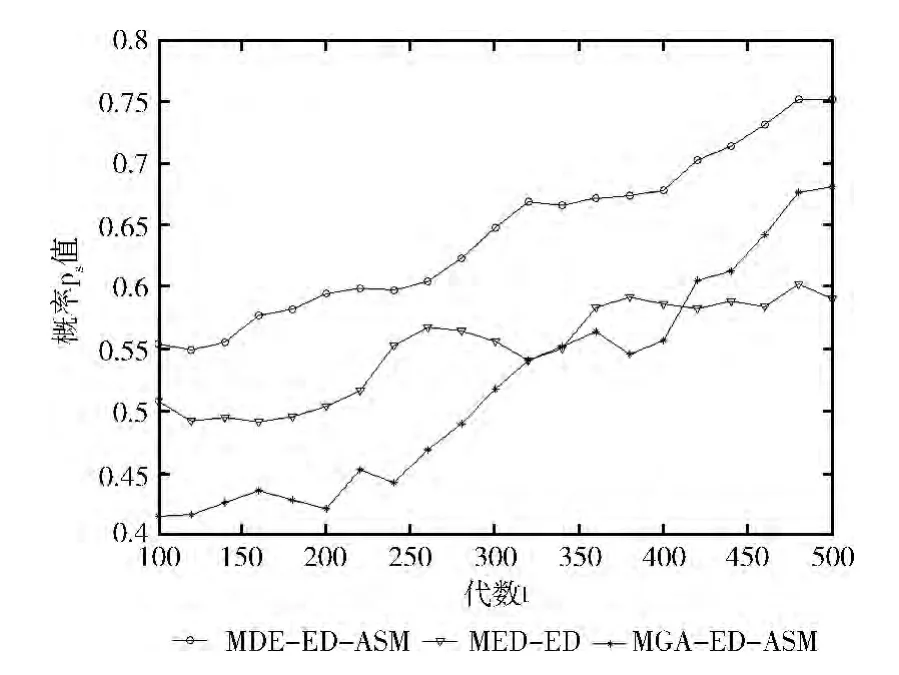
图4 代理模型和差分算子对概率ps 值的影响

从图3结果显示MGA－ED－ASM 能够更好的估计出一个稳定的最佳类数c，该值在F1函数中为7，而该函数最优解集在解空间中的流形分布可以看作是7段一维流形构成的。可见MGA－ED－ASM 估计出的类数较为准确地反映了流形的真实结构。

从图4结果显示MGA－ED 的选择概率整体向上爬升，但进化中出现较大的抖动。这是由于去除代理模型后，分布估计模型缺少足够的样本，影响了评估精度，需要更多借助差分算子来改善性能。

4 结束语

设计的基于分布估计和差分进化的多目标优化算法提出了基于RBF神经网络的代理模型，有效建立了分布估计模型、代理模型与Pareto最优解集所处流形之间的映射关系。通过多组优化问题的测试和分析验证了所提算法的性能。其整体性能好于同样适用分布估计模型的算法RMMEDA。此外，实验分析也表明差分算子和代理模型能够加快算法的优化速度，使其在同样函数调用次数下得到更好的优化结果。而代理模型中采用超体积指标自适应确定最佳类数c的方法，既避免了参数设置的问题，又较为准确评估出了流形的分段数量，提升了分布估计模型和代理模型的性能。

［1］GONG Maoguo，JIAO Licheng，YANG Dongdong，et al.Research on evolutionary multi－objective optimization algorithms［J］.Journal of Software，2009，20 （2）：271－289 （in Chinese）.［公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究 ［J］.软件学报，2009，20 （2）：271－289.］

［2］Zhou A，Qu BY，Li H，et al.Multiobjective evolutionary algorithms：A survey of the state of the art［J］.Swarm and Evolutionary Computation，2011，1 （1）：32－49.

［3］KONG Weijian，DING Jinliang，CHAI Tianyou.Survey on large－dimensional multi－objective evolutionary algorithms ［J］.Control and Decision，2010，25 （3）：321－326 （in Chinese）.［孔维健，丁进良，柴天佑.高维多目标进化算法研究综述［J］.控制与决策，2010，25 （3）：321－326.］

［4］LIANG Yujie，XU Feng.Adaptive hybrid multi－objective estimation of distribution evolutionary algorithm ［J］.Computer Engineering and Applications，2014，50 （5）：46－50 （in Chinese）.［梁玉洁，许峰.自适应混合多目标分布估计进化算法［J］.计算机工程与应用，2014，50 （5）：46－50.］

［5］LI Li，LI Yanyan.Multi－objective clustering ensemble algorithm based on knees solutions and differential evolution ［J］.Computer Engineering and Design，2014，35 （8）：2912－2916（in Chinese）.［李莉，李妍琰.基于热点解和差分进化的多目标聚类集成算法 ［J］.计算机工程与设计，2014，35 （8）：2912－2916.］

［6］Zhang Q，Zhou A，Jin Y.RM－MEDA：A regularity modelbased multiobjective estimation of distribution algorithm ［J］.IEEE Transactions on Evolutionary Computation，2008，12（1）：41－63.

［7］LONG Teng，GUO Xiaosong，PENG Lei，et al.Optimization strategy using dynamic radial basis function metamodel based on trust region ［J］.Chinese Journal of Mechanical Engineering，2014，50 （7）：184－190 （in Chinese）.［龙腾，郭晓松，彭磊，等.基于信赖域的动态径向基函数代理模型优化策略 ［J］.机械工程学报，2014，50 （7）：184－190.］

［8］LI Miqing，ZHENG Jinhua.An indicator for assessing the spread of solutions in multi－objective evolutionary algorithm［J］.Chiness Journal of Computers，2011，34 （4）：647－664（in Chinese）.［李密青，郑金华.一种多目标进化算法解集分布广度评价方法［J］.计算机学报，2011，34 （4）：647－664.］

［9］Ulrich T，Bader J，Zitzler E.Integrating decision space diversity into hypervolume－based multiobjective search ［C］／／In Proceeding of 12th Annual Conference on Genetic and Evolutionary Computation，2010：455－462.

［10］Bader J，Zitzler E.HypE：An algorithm for fast hypervolume－based many－objective optimization ［J］.Evolutionary Computation，2011，19 （1）：45－76.

［11］Mininno E，Neri，Cupertino F，et al.Compact differential evolution ［J］.IEEE Transactions on Evolutionary Computation，2011，15 （1）：32－54.

［12］ZHAN Teng，ZHANG Yi，ZHU Dalin，et al.Cellular multi－objective genetic algorithm based on multi－strategy differential evolution ［J］.Computer Integrated Manufacturing Systems，2014，20 （6）：1342－1351 （in Chinese）. ［詹腾，张屹，朱大林，等.基于多策略差分进化的元胞多目标遗传算法［J］. 计算机集成制造系统，2014，20 （6）：1342－1351.］

［13］LI Xueqiang，HAO Zhifeng，HUANG Han.Multi－objective evolutionary algorithm based on direction selection search ［J］.Journal of South China University of Technology （Natural Science Edition），2011，39 （2）：130－135 （in Chinese）.［李学强，郝志峰，黄翰.基于分方向选择搜索的多目标进化算法 ［J］.华南理工大学学报 （自然科学版），2011，39 （2）：130－135.］

［14］JIANG Yanjun，JIANG Jianguo，ZHANG Yuhua.Objectoriented reconfiguration of shipboard power network using multi－objective grid evolutionary algorithm ［J］.Electric Power Automation Equipment，2013，33 （3）：26－32 （in Chinese）.［蒋燕君，姜建国，张宇华.采用多目标网格进化算法并面向对象的舰船电网重构 ［J］.电力自动化设备，2013，33 （3）：26－32.］