基于AdaBoost改进的多分类器动态集成算法

姜季春，马 丹

（贵州大学 计算机科学与技术学院，贵州 贵阳550025）

0 引 言

根据集成过程中是否对待分类样本的具体特征进行自适应选取，多分类器集成方法被分为静态集成和动态集成两种类型［1－3］。和静态集成方法相比，动态集成方法可以在分类模型预测的过程中根据目标样本的特征和识别性能，实时地组合一组单分类器或调整其权重［4］。根据分类器在执行预测时的两种变化方式，得到应用于多分类器集成技术的动态集成方法有：动态选择 （dynamic selection）、动态投票 （dynamic voting）、以及结合动态选择和动态投票两种方法的混合集成方法［5，6］。这几种动态集成方法都可以有效提高集成分类的性能。目前一些实验也验证了动态集成分类器具有更好的针对性、灵活性和泛化能力，因此多分类器的动态集成无疑是进一步研究分类器集成技术的热点［7，8］。为了在应用领域中获得更好的分类性能，本文对当前最为流行的一种多分类器集成算法AdaBoost进行调整，在此基础上引入动态选择 （DS）的思想，得到一种改进的多分类器动态集成算法，并对比验证了该算法的分类效果。

1 调整AdaBoost算法

1.1 改进C4.5决策树

多分类器动态集成算法AdaBoost.MDS 是基于Ada－Boost算法提出改进的，改进的关键在于如何计算待分类样本和训练集之间决策属性的相关度。为了利用影响权重量化决策属性对于迭代生成分类模型的重要程度，进而引入属性相关度的计算模型，于是考虑以C4.5 决策树作为AdaBoost算法的基础学习方法，用于构造集成模型中的单分类器。样本权重在算法中描述该样本被抽取的概率，反映当前分类模型对其进行处理的难易程度。C4.5决策树中产生的残缺值采用分数实例的观念进行处理，对算法稍加调整即可直接处理带有权值的样本［9］。修改C4.5决策树算法，实际上是对信息熵和信息增益的公式定义进行调整。

定义1［10］假设训练集T 中包含p 个样本，这些样本分别属于m 个类，pi为第i 个类在T 中出现的样本个数，T 的信息熵为

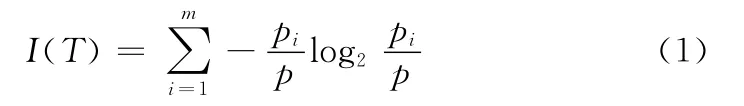
假设属性A 把集合T 划分成V 个子集 ｛T1，T2，…，TV｝，其中Ti所包含的样本数为ni，划分后的熵为

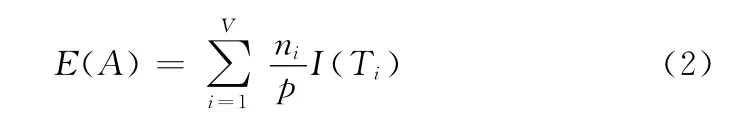
分裂后的信息增益为

信息增益率定义为信息增益与初始信息量的比值

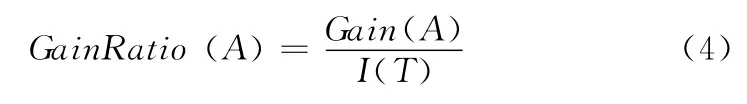
定义中的变量p、pi和ni，用来表示样本数量。改进C4.5决策树，即是将这3个变量重新定义为对应样本的权值之和。这样的调整使得在迭代分类模型的过程中仅需修改训练样本权重，从而避免了繁琐的重复抽样，降低了算法的实现难度。

1.2 调整后的AdaBoost算法过程描述

给出训练集、样本个数、训练次数和改进的C4.5决策树算法。调整后的AdaBoost算法训练过程描述如下：

（1）设初值：ωj（1）＝1／p，其中ωj（i）描述第i次迭代中第j个样本的权重。

（2）for i＝1，2，…，k do

1）使用C4.5决策树改进算法处理加权训练集T，获得单个分类器Ci。

2）计算Ci的分类误差ε（i）

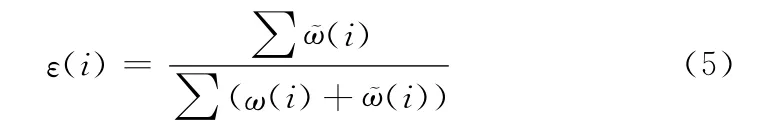
3）if（ε（i）＝＝0） （ε（i）≥0.5）then

exit

endif

4）计算每一条正确分类的样本权重

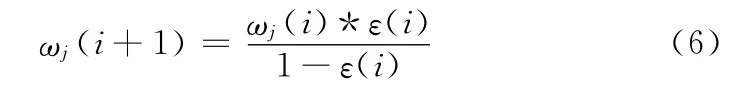
5）将每条样本的权值乘以原来的权值总和，再除以新权值总和。

end for

训练过程结束后得到分类模型，即一组固定的决策树序列 ｛C1，C2，…，Ct｝，其中 （t＜＝k）。利用训练过程产生的决策树组就可以预测待分类样本的所属类别。调整后的AdaBoost算法决策过程描述如下：

（1）设置所有类权重为0。

（2）for i＝1，2，…，t do

1）计算单分类器Ci的投票权重

2）得到待分类样本X 的类别c。

3）累加ω（Ci）得到类c的权重ω（C）。

end for

（3）返回ω（C）值最大的类。

以上为调整后的AdaBoost算法的过程描述。总的来说就是利用修改后的C4.5决策树算法直接处理带权样本，再根据分类结果对样本权重进行调整。训练过程的每一次迭代都要降低正确分类样本的权重，并且在后继迭代中着重处理分类困难的训练样本。根据对每条训练样本分类难度的评估值，构造一组互补型的单分类器。对待分类样本的类别预测则是使用加权投票的方式进行判别。

2 多分类器动态集成算法AdaBoost.MDS

2.1 算法的设计思想

AdaBoost算法的缺点在于一旦得到分类模型，对于所有待分类的目标样本均使用同一组固定的单分类器序列进行检测。这种以静态组合来集成单分类器的方式，在很大程度上影响了模型对待分类样本分类的准确率。为了弥补AdaBoost算法的不足，考虑将调整后的AdaBoost算法和动态选择 （DS）相结合，研究一种改进的多分类器动态集成算法。该算法通过比较待分类样本和训练集之间决策属性的相似程度，从固定的分类模型中动态选择出部分单分类器组成当前待分类样本的识别模型。

AdaBoost.MDS算法设计的重点在于如何引入待分类样本和训练集之间决策属性的相关度。图1为AdaBoost改进算法一次迭代得到的决策树。定义决策树中间结点的存储结构为 （attribute，w，p），叶结点存储结构为 （category，w，p），并设定决策属性attribute、目标类别category、影响权重w 和双亲结点的指针p。设w＝d＋1－l，其中d 为树的深度，l为结点所在层数。定义影响权重w 以表示决策树中不同层次的决策属性对于迭代生成分类模型的重要程度，且其重要性按层次逐渐下降。

按照从左到右的顺序从根开始逐层遍历决策树的决策属性，得到有效决策属性序列 ｛attribute1，attribute2，…，attribute n｝。定义训练集有效决策属性值的二维矩阵Bmn。以矩阵形式来存储所有的决策属性序列，从而保证有效决策属性序列的排列顺序和Bmn的列次序一致。如图2所示，tm（m∈N ∣1≤m≤k）表示训练集中的一条样本，其中k表示样本数量，n表示有效决策属性序列包含的值的个数。

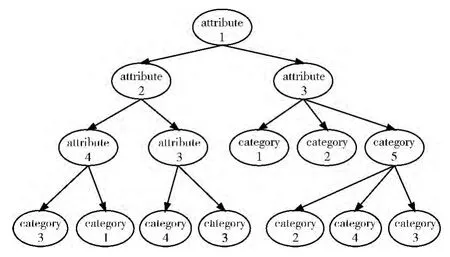
图1 AdaBoost改进算法一次迭代生成的决策树

图2 有效决策属性矩阵

预测时，按Bmn的列顺序排列待分类样本X（x1，x2，…，xs，c）的决策属性。重新排列待分类样本后得到X′（x1′，x2′，…，xn′），其中xj′表示待分类样本X 的决策属性按照Bmn的列顺序排列之后的第j 个属性值，而tij表示Bmn第i行第j 列的属性值。在此基础上，定义Fj（xj′，tij）统计有效决策属性矩阵Bmn第j 列中与X′的第j个属性值xj′相等的样本数目。函数定义如下

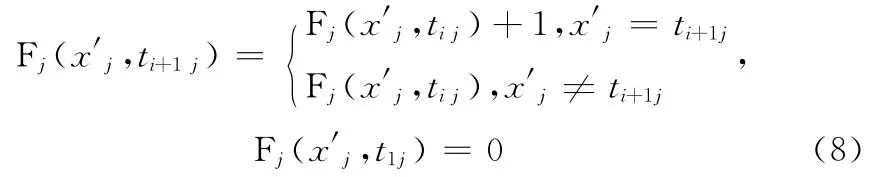
根据Fj（x′j，tij）得到属性相关度定义如下

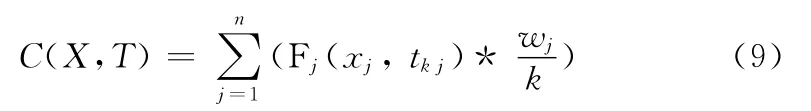
由上述定义可知，变量C（X，T）的取值反映了待分类样本与训练集决策属性特征之间的关系。C 的值越大表明X 与决策属性的特征分布越接近，即当前单分类器预测的类别与期望的分类结果越接近。

2.2 AdaBoost.MDS算法的过程描述

AdaBoost.MDI算法分为生成分类模型和预测结果两个阶段，其输入条件和上一章中AdaBoost改进算法一致。AdaBoost.MDI算法迭代分类模型的过程描述如下：

（1）设初值：ωj（1）＝1／k。（2）for i＝1，2，…，ndo 1）使用修改后的C4.5决策树训练单分类器Ci。

2）由Ci得到Bmn（i）。

3）计算Ci的分类误差ε（i）

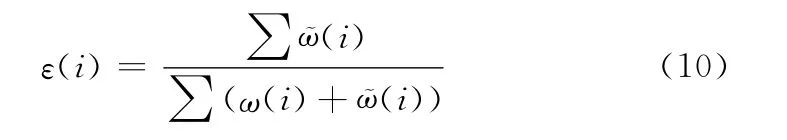
4）if（ε（i）＝＝0） （ε（i）≥0.5）then

exit

endif

5）计算每一条正确分类的样本的权重

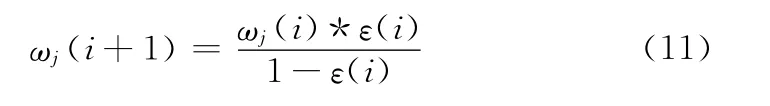
6）将每条样本的权值乘以原来的权值总和，再除以新权值总和。

endfor

训练过程结束后得到一组固定的决策树序列 ｛C1，C2，…，Ct｝和训练集有效决策属性矩阵序列 ｛Bmn（1），Bmn（2），…，Bmn（t）｝。预测之前需给定待分类样本和单分类器的个数阈值，预测时利用训练过程输出的结果得到待分类样本的类别。AdaBoost.MDI算法预测待分类样本的过程描述如下：

（1）动态选择f 个单分类器构建识别模型，f 为分类器的个数阈值。

1）根据矩阵Bmn的列次序排列待分类样本X（x1，x2，…，xt，c），得到X′（x1′，x2′，…，xt′）。

2）for i＝1，2，…，t do

计算相关度C（X，Ti）。

endfor

4）模糊综合评价法：模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。该方法可分为单层和多层次模糊综合评判[7]。

3）根据C（X，Ti）的计算值，在迭代分类模型之后输出的一组分类器中从大到小地选择出f 个单分类器，组成当前待分类样本的识别模型 ｛C′1，C′2，…，C′f｝。

（2）对每个类的权值赋0。

（3）for i＝1，2，…，fdo

1）计算

得到预测类别c。

2）累加ω（Ci）得到类c的权重ω（C）。

endfor

3 实验结果分析

AdaBoost.MDS算法是在调整后的AdaBoost算法基础上进行改进的。为了更好地分析AdaBoost.MDS算法的分类效果，先将调整后的AdaBoost算法与几种常用分类算法的实验结果作比较，再分析AdaBoost.MDS 算法的分类性能。

3.1 实验1对比调整后的AdaBoost算法性能

实验使用UCI（University of California Irvine）机器学习数据库中的数据集验证分类算法的性能。经过预处理步骤之后，每条样本选取20个决策属性和1个类标号属性。从数据集中选取部分样本作为训练集用来生成分类模型，余下的样本可作为测试集以预测模型的性能。实验1 中，先将训练集划分比例设置为60%。常用的分类学习算法可直接从weka中调用。使用MyEclipse和weka平台实现改进算法的编写，其参数采用weka中的默认设置，并在平台中进行实验数据处理和算法分类性能的测试。7 种分类算法在该训练集中建模并在测试集上进行预测，得到的实验结果见表1。

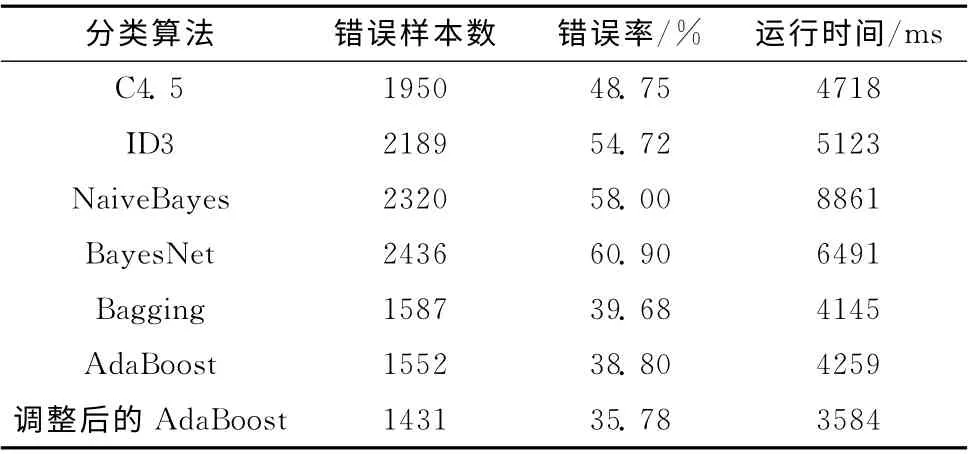
表1 7种分类算法实验结果对比

由表1可见，Bagging、AdaBoost、调整后的AdaBoost 3种集成算法的分类错误率和运行时间均低于其它4种单分类算法，并且调整后的AdaBoost算法所得模型的分类错误率最低，耗时最少。

采用交叉测试法将训练集的比例按照20%、40%、60%和80%进行划分，每种算法在4种比例的训练集中均生成一个分类模型。使用多组待分类样本，分别对3种算法的分类模型进行测试。预测后得到Bagging、AdaBoost、调整后的AdaBoost这3种集成算法在4种比例训练集中的分类错误率如图3所示。

图3 3种集成分类算法的实验结果对比

由图3可见，和两种流行的分类集成算法相比，在不同划分比例的训练集中，调整后的AdaBoost算法取得的分类错误率最低。并且随着训练样本数据规模的增加，调整后的AdaBoost算法的分类错误率下降幅度最小。

综合二项实验结果来看，相较于单分类算法而言，集成分类算法的分类错误率更低。和流行的单分类算法、集成分类算法相比较，调整后的AdaBoost算法耗时短，分类精度更高。

3.2 实验2AdaBoost.MDS算法性能分析

为了更好地对比实验结果，AdaBoost.MDS算法性能分析使用的数据集、实验环境与实验1相同。实验仍然按照20%、40%、60%、80%4种比例从数据集中抽取所需的训练集，得到training sets 1、training sets 2、training sets 3和training sets 4。分类集成算法AdaBoost、调整后的AdaBoost和动态集成算法AdaBoost.MDS在4个训练集中各自生成分类模型。每个分类模型均在4种划分比例的数据集中经过多次预测，得到平均分类准确率见表2。

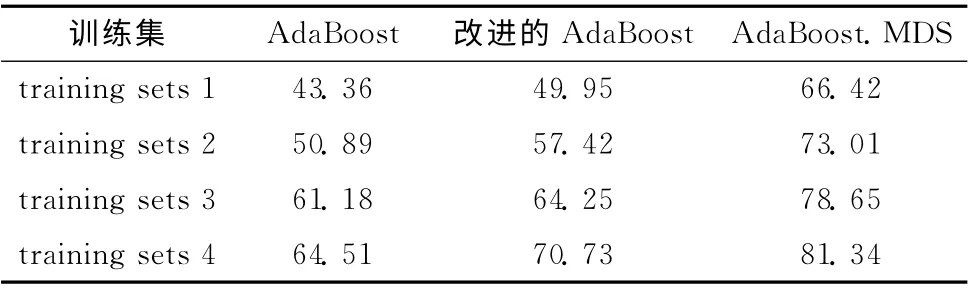
表2 AdaBoost.MDS算法实验结果对比／%

在上述实验的基础上改变样本决策属性的数量，以进一步测试算法的准确率和泛化能力。3 种集成算法在不同的样本条件下重新生成分类模型，预测后得到模型的分类准确率如图4、图5、图6所示，图中X 轴表示训练样本决策属性数量，Y 轴表示训练样本集合在数据集中的划分比例，Z轴表示算法的分类准确率，图中的曲面表示分类集成算法在不同划分比例的训练集和不同数量的样本决策属性下的分类结果。

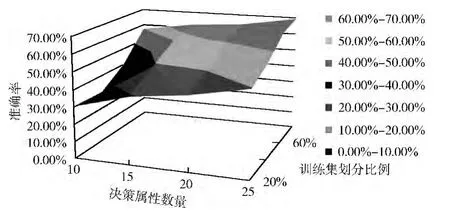
图4 AdaBoost算法在不同样本条件下的分类准确率

对比图4、图5、图6 可知，除了AdaBoost算法在训练集划分比例从20%增加到40%，且样本的决策属性数目较少时，其分类准确率有所下降以外，随着有效范围内样本决策属性的增加，3 种分类集成算法的识别模型在图中其它结点处的分类准确率都呈现上升趋势。

图5 调整后的AdaBoost算法在不同样本条件下的分类准确率

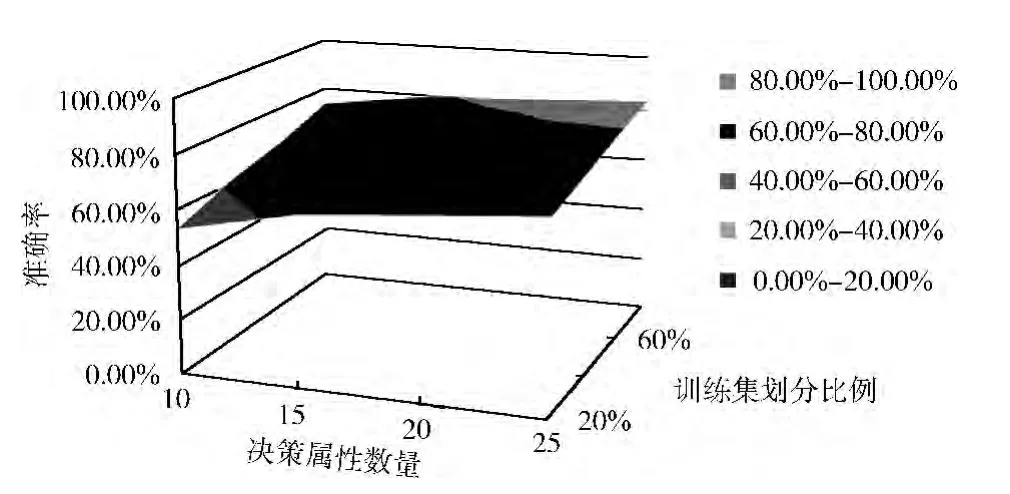
图6 AdaBoost.MDS算法在不同样本条件下的分类准确率

综合分析以上实验结果，可以发现不管和单分类器还是静态集成分类算法相比，AdaBoost.MDS算法在4 种划分比例的训练集以及不同样本决策属性数量的条件下都取得了最高的分类准确率。并且随着训练集划分比例和决策属性数量的增加，AdaBoost.MDS算法所得模型的分类准确率上升幅度最小，说明该算法受抽取样本的影响最小，算法的稳定性好，有效提高了分类精度和泛化能力。

4 结束语

本文通过改进调整后的AdaBoost算法，研究了一种多分类器动态集成算法AdaBoost.MDS。算法中引入属性相关度的定义以评价待分类样本和训练集之间特征的相似程度，实现从待集成的一组固定序列的单分类器中动态选择出部分与当前待分类样本特征相似的单分类器组成识别模型。实验结果表明，基于调整后的AdaBoost算法和动态选择 （DS）相结合的改进算法AdaBoost.MDS 在分类准确率、运行时间、泛化能力几项性能指标上均有较大的优势。

［1］ZHANG Xin.Classification－based data integration method［D］.Guangdong：Computer College of Guangdong University of Technology，2013 （in Chinese）. ［张鑫.基于分类的数据集成方法 ［D］.广东：广东工业大学计算机学院，2013.］

［2］Chen L，Kamel MS.A generalized adaptive ensemble generation and aggregation approach for multiple classifier systems［J］.Pattern Recognition，2009，42 （5）：629－644.

［3］GUAN Jinghua，LIU Dayou，JIA Haiyang.An adaptive ensemble learning method of multiple classifiers ［J］.Journal of Computer Research and Development，2008，45 （Sl）：218－221 （in Chinese）.［关菁华，刘大有，贾海洋.自适应多分类器集成学习算法 ［J］.计算机研究与发展，2008，45 （Sl）：218－221.］

［4］Ko AHR，Sabourin R，Britto AS.From dynamic classifier selection to dynamic ensemble selection ［J］.Pattern Recognition，2008，41 （5）：1735－1748.

［5］Chen Bing，Zhang Huaxiang.An approach of multiple classifiers ensemble based on feature selection［C］／／Fifth International Conference on Fuzzy Systems and Knowledge Discovery，2008.

［6］CHEN Bing，ZHANG Huaxiang. Dyanmic combinatorial method of multiple classifiers on emsemble learning ［J］.Computer Engineering，2008，34 （24）：218－220 （in Chinese）.［陈冰，张化祥.集成学习的多分类器动态组合方法 ［J］.计算机工程，2008，34 （24）：218－220.］

［7］GUO Hongling，CHEN Xianyi.Method of selective multiple classifiers ensemble ［J］.Computer Engineering and Applications，2009，45 （13）：186－188 （in Chinese）.［郭红玲，程显毅.多分类器选择集成方法 ［J］.计算机工程与应用，2009，45 （13）：186－188.］

［8］HAO Hongwei，WANG Zhibin，YIN Xucheng，et al.Dynamic selection and circulating combination for multiple classifiers systems［J］.Acta Automatica Sinica，2011，37 （11）：1290－1295 （in Chinese）.［郝红卫，王志彬，殷续成，等.分类器的动态选择与循环集成方法 ［J］.自动化学报，2011，37（11）：1290－1295.］

［9］WANG Bing.The mathematical analysis of AdaBoost algorethm ［J］.Software，2014 （3）：96－97 （in Chinese）. ［王兵.AdaBoost分类算法的数学分析［J］.软件，2014 （3）：96－97.］

［10］CHEN An，CHEN Ning，ZHOU Longxiang，et al.Data mining technology and application ［M］.Beijing：Science Press，2006 （in Chinese）. ［陈安，陈宁，周龙骧，等.数据挖掘技术及应用 ［M］.北京：科学出版社，2006.］