基于MHT的网络化雷达抗干扰算法
2015-12-23张建军
张建军
(中国人民解放军92941部队93分队,辽宁 葫芦岛125001)
0 引 言
网络化雷达集成了其组成雷达的资源并进行了信息融合,整体作战能力极大提高[1]。分布式干扰将多个电子干扰机布置在特定区域,自动或受控地对目标进行干扰,相比于传统干扰机更易进入目标雷达回波信号主瓣[2]。分布式干扰具有设备简单、分布范围广等特点,有文献对分布式干扰机的干扰性能进行了研究[3-5],常规的抗干扰方法对分布式干扰效果不理想,在分布式干扰的情况下,需要进一步研究如何提高雷达的抗干扰能力,实现对敌目标的有效检测。
分布式干扰区域中,雷达对目标的检测概率下降,并且雷达接收机数据量增加,为防止接收机饱和,需要提高虚警的检测门限,雷达目标检测门限的降低伴随着虚警增加,所以需要研究抗分布式干扰的目标检测算法。多假设跟踪 (MHT)方法是处理数据关联的最佳方法[6],MHT方法通过延迟决策实现了信息量在延迟中的积累,该算法由当前测量值和历史测量值共同决定,适用于信噪比低的系统。本文提出了基于MHT 的网络化雷达目标检测算法,该算法利用MHT 在分布式干扰抑制中的优良特性,并通过秩K 融合规则得出目标的检测概率。仿真结果表明,本文算法能够有效抑制分布式干扰,是一种有效的网络化雷达抗干扰算法。
1 MHT算法
1.1 MHT算法原理
理想情况下,MHT 方法是数据关联的最佳算法。MHT 数据关联依赖于历史测量结果和当前测量,MHT 具体处理流程如图1所示。
(1)数据聚簇:基于聚簇的假设和目标是MHT 的处理对象,将新接收到的测量点迹与假设相关联并进行更新。若测量点与旧簇不相关,则形成新簇,若两个独立簇与同一测量点相关,则这两个簇形成一个超簇。
(2)假设生成:对每一个回波信号要考虑出现新目标的可能性,同时需要考虑虚警的可能性。设k时刻的假设是k-1时刻的假设与当前时刻数据关联的结果。

图1 MHT 具体处理流程[7]
(3)假设删除:去除不可行的假设。
(4)假设矩阵管理:假设生成和删除是多假设跟踪算法的核心,如果缺少合理的策略,则算法产生的假设数目、目标数以及需要处理的数据量会非常巨大。确定合理策略进行假设生成和删除,是MHT 算法的关键步骤。
1.2 改进的m-最优MHT算法
m-最优MHT 算法是在MHT 算法基础上的优化算法,其核心思想是在得到的量侧数据中去除低概率假设,只保留m 个最优假设,假设t时刻有m(t)个假设,则下一时刻假设数目限定在m(t+1)个内,m 是可变参数,可以给定,也可以自适应选择。该算法的主要步骤为[8]:①对先验目标状态和初始假设生成进行初始化;②接收新的目标量测数据和干扰数据;③对目标进行更新;④形成新的聚类,聚类由可能的航迹以及与航迹关联的量测组成,若前时刻任意两聚类与当前量测相关,则形成超聚类;⑤计算每个假设的概率,进行假设目标和量测更新,形成新的假设集;⑥用m-最优算法对关联假设进行删减,去掉小概率假设,保留最优的m 个假设;⑦简化聚类中的假设矩阵,对于目标概率为1的确定为目标,并创建新的聚类。
m-最优MHT 算法存在的主要问题是:当目标和干扰较大时,在聚簇过程中将产生高维矩阵,使生成的假设数量增多,导致假设的删减过程也非常复杂,算法实现时间变长,本文研究了雷达目标和干扰较大时,从聚矩阵维数下降的角度提出了m-最优MHT 算法的改进算法。由于新目标的不断加入,m-最优MHT 算法引入Bar-shalom 聚矩阵后的行向量维数变得很高,而如果将对已知目标的跟踪和新航迹的起始分开进行考虑,对目标跟踪中所产生的新目标起始过程单独计算,则目标跟踪过程中的矩阵维数将下降,简化为m× (n+2),新目标均处于矩阵的一列。这样在不影响假设矩阵量的同时,算法执行时间将大幅缩减,对工程实现有较大作用。
2 秩K 融合规则
网络化雷达采用决策融合结构对雷达进行控制,秩K融合规则是决策融合模型采用的融合规则[9]。其具体规则为:假设网络化雷达系统有N 个接收站,如果至少有K 个接收站判断目标存在,则雷达认为目标存在。如果K=1,对应 “or”规则,如果K=N,则对应 “and”规则。秩K 融合规则的判决流程如图2所示。

图2 秩K 融合规则的判决流程
假设雷达系统网内有N 个接收站,每个接收站对目标的探测是否存在做出硬判决。硬判决指检测器判决结果为0或1,假设判决结果为目标存在,则表示为H1,如果判决结果为目标不存在则表示为H0,则第n 个接收站的决策值dn表述如下

其中n= (1,2…N)。
接收站将自身判决结果输入网络化雷达融合中心,融合中心根据局部判决结果形成的判决向量产生全局判决D0,表示如下


综上,秩K 融合判决规则如下式此时,雷达网络中心对目标的融合发现概率为

式中:S1——各接收机判决为 “1”的向量D 集合,S0——各接收机判决为 “0”的向量D 集合,Pdn——第n 个接受机对目标的发现概率。此时,网络化雷达对目标的虚警概率表示如下

式中:Pfn——第n个接受机对目标的虚警概率。
由上式可以看出,参数K 的大小直接决定着判决准备准则,进而影响雷达系统的发现概率和虚警概率,所以参数K 的选择非常重要。下面分析K=1和K=N 的两种情况,当K=1时,只要有1个雷达接收机发现目标,则融合系统即认为发现了目标,此时,雷达系统的融合发现概率和虚警概率为

据上式分析,K=1时,较低的单接收机发现概率即可得到比较高的融合发现概率。
进一步分析融合虚警概率,假设各接收机的虚警概率均相同为Pfi=Pf0,i=1,2,…N。
则融合虚警概率为
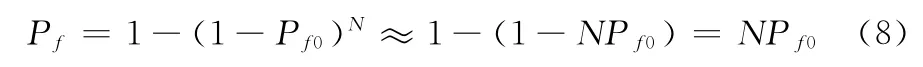
可见融合系统的虚警概率是单个接收站虚警概率的N倍。虚警概率大幅提高。
当K=N 时,所有雷达接收机发现目标,则融合系统才认为发现了目标,此时,融合系统的目标发现概率和虚警概率分别为
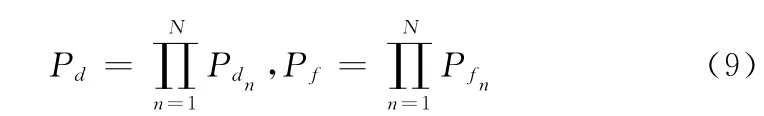
由此可见,K=N 时,融合系统可以得到较小的虚警概率,而同时,发现概率也较小。
网络化雷达系统经信息融合后得到的合理结果应该是:融合发现概率大于单接收机的发现概率,而融合虚警概率小于单接收机的虚警概率,所以对于秩K 的选择非常关键,在工程中应分别计算不同K 值对应的发现概率和虚警概率,进而获得最佳K 值。
3 干扰识别
本文研究分布式干扰下的雷达抗干扰算法,分布式干扰与集中式干扰具有不同的特性,雷达对这两种干扰采用的抗干扰算法也有所不同,根据分布式干扰与集中式干扰空间距离差的不同可以判别干扰属于哪一种[10],如果干扰源识别为分布式干扰,则利用文中提出的算法,进行雷达目标的抗干扰识别。
如图3所示,J0为集中式干扰机,R1、R2、R3为三部雷达,J1、J2、J3为分布式干扰机,分布式干扰机由于功率较小,只能干扰距离较近的雷达,J0作为大功率干扰机,可以同时干扰R1、R2、R3。设雷达的干扰源方向角为θ^i,i,j=1,2,3,则以雷达为顶点,按照方向角角度做直线,两两直线的交点为oij,焦点坐标为(xij,yij)


图3 雷达及干扰
该点的互协方差为

其中l=3,xsji=xsj-xsi,ysji=ysj-ysi(xij,yij),(xil,yil)两点之间的距离差为

则距离差的均值和方差如下

式中:ρ——Δx 与Δy 之间的相关系数。

式中:G——χ2检验中显著性水平的门限值,如果结果为1,则表示为集中式干扰,若为0则表示干扰为分布式干扰。
4 基于MHT的网络化雷达抗干扰算法
基于以上叙述及理论,本文提出了基于MHT 的网络化雷达抗干扰算法,主要步骤为:
步骤1 通过干扰判断方法,判断当前雷达环境中的干扰为分布式干扰还是集中式干扰,如果判断为分布式干扰则进行步骤2。
步骤2 采用本文改进的m-最优MHT 算法,利用Bar-Shalom 联合数据互联滤波算法计算每一个事件概率。
步骤3 用文中第2部分所述的秩K 融合准则计算融合后的概率,进而判断每一个目标的状态。
5 仿真结果及分析
5.1 仿真思路及数据
建立化雷达仿真模型,建立干扰模型,对网络化雷达进行分布式干扰,由于受到网络分布式干扰,网内的雷达无法同时对目标完成连续探测,但网络化雷达的各个分雷达会在不同时间段达成对目标的探测。首先构造一条航迹,在网络化雷达探测探测中,每个雷达会各自获得一组点迹,运用本文所述算法合成轨迹,进行分析。
仿真具体参数设置如下:雷达参数:数量3 个,位置(km):(0,350),(0,0),(200,500),雷达天线的发射及接收增益为30db,雷达波长为0.1m,副瓣增益为-5db,雷达扫描周期为1s,发射功率300kw。干扰机参数:数量5个,位置(km): (100,300), (250,150), (0,200),(500,400),(30,450),天线增益22db,干扰功率10w 带宽10Mhz,干扰机功率损耗2db。目标参数:数量2个,做匀速直线运动,目标RCS为10m2杂波为正态分布。
5.2 仿真结果分析
从仿真结果图4中可以看出,应用本文算法,网络化雷达克服了分布式干扰下,雷达存在部分盲区,航迹不连续现象,最后融合得到的航迹精度较高,且算法运行时间较短,从图5中可以看出算法的均方根误差较小,在可接受的范围。本文算法能够有效对抗分布式干扰造成的航迹不连续、目标丢失的问题,是一种有效的雷达抗干扰算法。

图4 仿真结果
6 结束语

图5 均方根误差
分布式干扰具有设备简易、干扰范围广等特点。分布式干扰下,单雷达目标检测概率下降、检测性能变差、航迹不连续。基于此,本文研究了分布式干扰下网络化雷达抗干扰算法,该算法基于改进的MHT算法与秩K 融合规则进行目标的检测,首先针对传统MHT 算法计算量大不利于工程实现的特点,研究了降低算法复杂度的方法,然后利用秩K准则计算融合后的目标检测概率并实现目标航迹检测。仿真结果表明了本文算法在雷达抗分布式干扰中的有效性。
[1]GUO Jianming,TAN Huaiying.Overview of radar technology development and initial study on the 5th generation of radar[J].Modern Radar,2012,34 (2):1-7 (in Chinese).[郭建明,谭怀英.雷达技术发展综述及第五代雷达初探 [J].现代雷达,2012,34 (2):1-7.]
[2]LOU Xiaoxiang,ZHENG Hao.Algorithm based on multiple hypothesis target tracking [J].Command Information System and Technology,2012,3 (6):36-38 (in Chinese). [楼 晓祥,郑浩.基于多假设目标跟踪算法 [J].指挥信息系统与技术,2012,3 (6):36-38.]
[3]CHEN Chunfeng,LUO Wencheng.Selected filter of MHT method for complex environment [J].Computer Engineering and Applications,2013,49 (15):229-232 (in Chinese).[陈春风,骆文成.复杂条件下MHT 方法的滤波器选择 [J].计算机工程与应用,2013,49 (15):229-232.]
[4]FANG Mingxing,WANG Jiegui,YANG Yongjing.Evaluation on netted radar detection performance in the distributed jamming of multi-false target[J].Mordern Defence Technology,2014,42 (3):135-141 (in Chinese).[房明星,王杰贵,杨永晶.分布式多假目标干扰下组网雷达监测性能分析 [J].现代防御技术,2014,42 (3):135-141.]
[5]REN Bo,SHI Longfei,WANG Hongjun,et al.Investigation on of polarization filtering scheme to suppress GSM interference in radar main beam [J].Journal of Electronics &Information Technology,2014,36 (2):460-463(in Chinese).[任博,施龙飞,王洪军,等.抑制雷达主波束内GSM 干扰的极化滤波方法研究 [J].电子与信息学报,2014,36 (2):460-463.]
[6]LI Shizhong,WANG Guohong,BAI Jing,et al.A tracking algorithm with multiple probabilities hypothesis for radar network point target in the presence of suppressive jamming [J].Journal of Xian Jiaotong University,2012,46 (10):101-105(in Chinese).[李世忠,王国宏,白晶,等.压制干扰下雷达网点目标概率多假设跟踪算法 [J].西安交通大学学报,2012,46 (10):101-105.]
[7]RAO Shijun,JIANG Ning,ZHANG Yunwen.Optimization and simulation of multiple hypotheses target algorithm tracking based on structures branching [J].Computer Simulation,2013,30 (1):18-21 (in Chinese).[饶世钧,姜宁,张云雯.基于结构多假设目标跟踪算法优化与仿真 [J].计算机仿真,2013,30 (1):18-21.]
[8]YANG Rennong,CHEN Yan,WU Meng,et al.A tentative study on the approaches to track initiation [J].Computer En-gineering & Science,2012,34 (2):176-179 (in Chinese).[杨任农,陈岩,邬蒙,等.M-最优假设组合航迹关联算法[J].计算机工程与科学,2012,34 (2):176-179.]
[9]HAN Guoxi,HE Jun,QI Jianqing.Fused detection probability model of NRCS based on rank k criterion [J].Journal of Naval University of Engineering,2014,26 (1):65-69 (in Chinese).[韩国玺,何俊,祁建清.基于秩K 准则的网络雷达对抗系统融合发现概率计算模型 [J].海军工程大学学报,2014,26 (1):65-69.]
[10]XU Haiquan,WANG Guohong,GUAN Chengbin.Target tracking technique for radar network under the distributed jamming [J].Acta Armamentarii,2011,32 (6):765-769(in Chinese).[徐海全,王国宏,关成斌.分布式干扰下雷达网 的 目 标 跟 踪 技 术 [J].兵 工 学 报,2011,32 (6):765-769.]
