两类特殊图的距离谱
2015-12-23贾会才,胡李宁
两类特殊图的距离谱
贾会才, 胡李宁
(河南工程学院 理学院,河南 郑州 451191)
摘要:图的距离谱问题是指图的距离矩阵的特征值问题.主要研究了具有特殊结构的两类图的距离谱问题,计算了这两类图的距离特征多项式,获得了它们的距离谱,对于研究图的距离谱确定问题具有重要意义.
关键词:图谱理论;距离矩阵;距离谱
中图分类号:O157.5 文献标志码:A
收稿日期:2015-05-25
基金项目:河南省教育厅科学技术研究重点项目(13B110939)
作者简介:贾会才(1981-),男,河南许昌人,讲师,主要从事图论研究.
图谱理论主要研究图的邻接矩阵、拉普拉斯矩阵、无符号拉普拉斯矩阵及距离矩阵等图的重要矩阵特征值问题,是组合矩阵论和代数图论的重要研究领域.图的距离矩阵经常出现在通信网络设计、图的嵌入设计、分子稳定性及网络流算法等领域.距离谱问题在量子化学、物理学、计算机科学、通信网络及信息科学等领域均有广泛应用.目前,图的距离谱问题主要集中在刻画给定图类中图的距离谱半径取得最大或者最小的图[1-4]、图的距离特征值的分布及图的距离谱确定问题[5].本课题主要研究了具有特殊结构的两类图的距离谱问题,计算了这两类图的距离特征多项式,从而获得了它们的距离谱,对于研究图的距离谱确定问题具有重要意义.
1基本概念和结论
定义1图G是一个三元组,记作G=
(1)图G的顶点或结点v1,v2,…,vn组成顶点集,记作V(G)={v1,v2,…,vn}(V(G)≠Ø) ;
(2)图G的边e1,e2,…,em组成的边集记作E(G)={e1,e2,…,em};
(3)φ(G):E→V×V称为关联函数.
定义2图G的距离矩阵D定义为D=D(G)=(dij)=dG(vi,vj) .
定义3D(G)的特征值及其特征值的重数构成了图G的距离谱.
定义4设图G的距离矩阵为D, 则图G的距离特征多项式定义为det(λI-D).
参考文献上述未介绍的符号和术语可[6].
2中心团与多个悬挂团相连(join)的图的距离谱问题
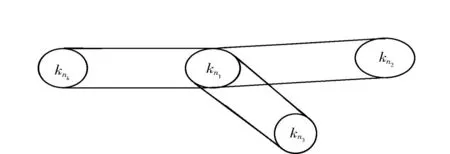
图1 图G 1 Fig.1 Graph G 1
图G1(见图1):中心团与悬挂团相连(join), 是指中心图中每一个点与悬挂团中每一个点都连边.显然,同一个团内点之间的距离为1,中心团与悬挂团的点之间距离为1, 而悬挂团点之间的距离为2.因此,图G1的直径为2.
2.1图的距离矩阵表示
在图1中,团kn1中的点与团kn2,kn3, …, knk之间的点的距离为1; 团kn2,kn3, …, knk中点之间的距离为2,且有n1+n2+…+nk=n.图G1的距离矩阵表示为

2.2图的距离谱求解
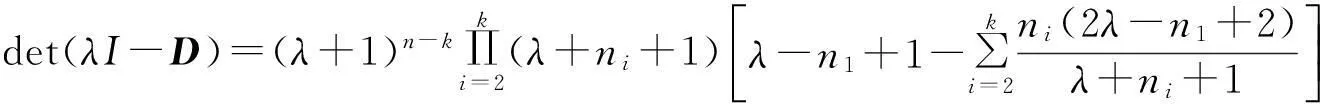
证明 经过计算

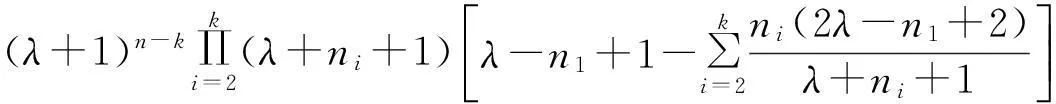
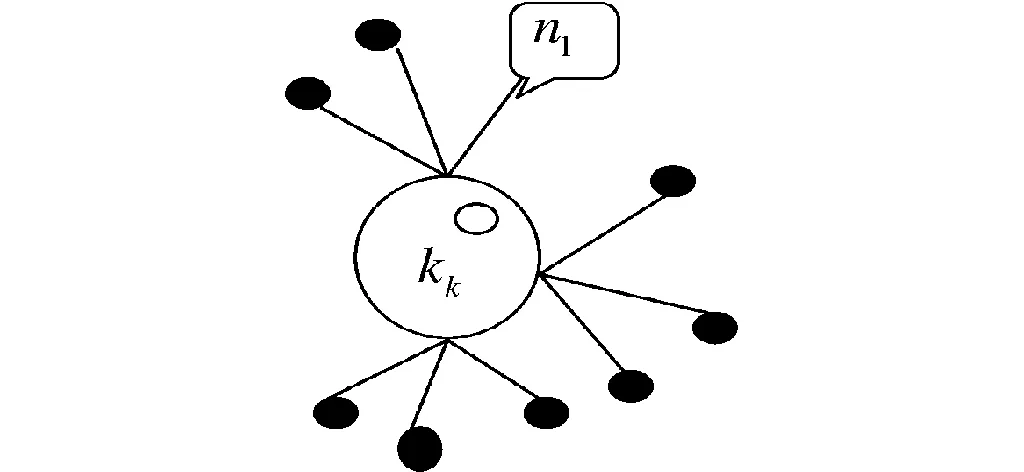
图2 图G 2 Fig.2 Graph G 2
3团每个点都连一些悬挂点的图的距离谱问题
图G2如图2所示,中心团每个点都连一些悬挂点.
3.1图的距离矩阵表示
如图2所示,团kk中每个点都连一些悬挂点,团内第i个点连ni个点.同一个团内点之间的距离为1;ni内点与团中除第i个点外的其余点之间的距离为2;ni内任意两个不同点之间的距离为2;ni内的点与n1,…,ni-1,ni+1,…,nk内的点之间距离3.因此,图G2的直径为3.距离矩阵可以表示为

3.2图的距离谱求解

证明经过计算


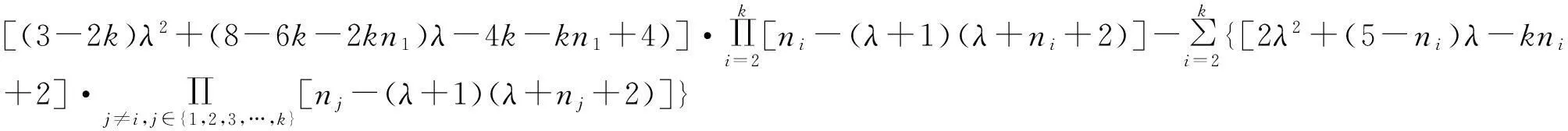
参考文献:
[1]IlicA.Distancespectralradiusoftreeswithgivenmatchingnumber[J].DiscreteApplicationofMathematics,2010(158):1799-1806.
[2]LinH,YangW,ZhangH.Distancespectralradiusofdigraphswithgivenconnectivity[J].DiscreteMathematics,2012(312):1849-1856.
[3]YuG,WuY,ZhangY.Somegrafttransformationsanditsapplicationonadistancespectrum[J].DiscreteMath,2011(311):2117-2123.
[4]ZhangX.Onthedistancespectralradiusofsomegraphs[J].LinearAlgebraApplication,2012(437):1930-1941.
[5]LinHQ,HongY,WangJF,etal.Onthedistancespectrumofgraphs[J].LinearAlgebraApplication, 2013(439):1662-1669.
[6]BondyJA,MurtyUSR.GraphTheorywithApplications[M].London:MacmillanPublishersLimited,1976.
Distance spectra of two kinds of graphs with special structure
JIA Huicai, HU Lining
(CollegeofSciences,HenanInstituteofEngineering,Zhengzhou451191,China)
Abstract:The problem on the distance spectra of graphs refers to that on the eigenvalues of distance matrix of graphs. This paper mainly investigates the distance spectra of two kinds of graphs with special structure, providing the distance characteristic polynomial and obtaining their distance spectra. This plays an important role to the problem on the distance spectrum characterization of graphs.
Key words:spectral graph theory; distance matrix; distance spectrum
