备件配置的优化设计探讨
2015-12-23丁定浩
丁定浩
(中国电子科技集团公司电子科学研究院,北京 100041)
备件配置的优化设计探讨
丁定浩
(中国电子科技集团公司电子科学研究院,北京 100041)
备件配置的优化设计,国内外迄今没有给出系列的理论和设计模型。当前行销的国外备件保障设计的商业软件,既没有说明理论根据,也没有公布仿真模型,其正确性难以辨别。从实际的设计结果来看,既不合理,更谈不上优化设计,通常是极其保守的设计。为此,开发了相应的优化设计软件,其合理性和正确性均可用理论模型和仿真试验来证明。
备件配置; 备件保障; 备件供应体制;备件补充方式
0 引言
装备的备件配置,特别是军用装备的备件配置,涉及战备完好和降低寿命周期费用的关键环节。现场一旦缺少任一故障部件的备件,就将导致装备无法准时出动而延误战机。但配置不当,也会导致备件长期积压,寿命周期费用大幅地上升。
当前行销的相应国外软件,其设计结果表明,它的设计方针中包含了以价格高低来配置备件的因素,以期降低备件的费用。但实际设计的前提,则首先必须满足备件得到指定保障概率的要求,而备件的保障概率取决于备件对象的失效率高低和取得相应备件的周转时间,与价格高低无直接关系。多配价格低廉的备件所得到的备件保障的高概率,无法抵消少配价格高昂备件保障的低概率。因此,这些多配的备件是多余的,对提升备件保障概率是无用的。这点在上述设计结果中表现得非常明显。
上述软件存在另一个问题是设计目标是以使用可用性来取代战备完好率。这是两个完全不同的参数,不能混淆,见文献 [1-4],此处不再复述。
从国外已经发表的一部分文献[5]来看,消耗性备件保障概率的理论模型也是背离客观实际的。无论对单个部件还是系统的备件保障概率,均低估了实际的备件保障概率。就系统的备件保障概率的模型来说,不少国外文献用部件保障的联合概率来表示系统的保障概率,也就是以部件的保障概率的乘积模型来表达系统的备件保障概率。难得见到国家军用标准提出了与此不同的模型,它取系统组成单元中备件保障概率最低的概率作为系统的备件保障概率,这对改进连乘模型的保守性有利,但它同样不符合客观实际,这一模型的创建者提不出理论依据,宣称是用仿真试验得出的。 这说明不对数字仿真模型作正确性鉴定,一旦采用数字仿真试验就以为能保证结果的正确性是荒谬的。
对于可修部件的备件保障概率模型,一直使用由动态维修的马尔柯夫随机过程导出的。但它只能适应现场维修的场合,不能适应要经历运输到达外地维修的过程,在这种场合下,就会出现即使配置无穷多的备件也不能达到高概率的备件保障要求的情况,而这是背离客观实际的。
总之,国外现行备件保障模型均低估了实际的保障概率,因而报导中常常出现备件的积压事件。例如:1990年,英国国防部积压库存70亿美元的备件成了废弃物,美国国防部则超过340亿美元。在1997年,美国商用航空工业备件的库存积压超过520亿美元,其中有230亿美元备件尚可修复,还有290亿美元只能废弃。据估计,商用航线工业的备件过剩数字处于25%~40%之间。在1993-1997年间,商用航空的备件从7%~10%的年复比增加,大大高于交通和机群增长的速度。
但是备件的积压,并不表示备件保障已经过头,实际上只要有少数备件不足,就有缺件发生而延误战机。
1 符合客观实际的3个备件保障概率的基础模型
下面是3个不同于现有的、但符合客观实际的、适用于消耗性备件的保障概率的基础模型:一个是更换模块的备件保障概率模型,两个是系统的备件保障概率模型;其中一个是适应任务的剖面为间断工作的备件保障概率模型,另一个适应于任务剖面是连续工作状态的模型。
当备件对象的寿命为指数分布时,其失效率为λ,现场配置的备件数量为m,历经t0工作时间当发生失效后能有备件更换的保障概率p0为泊松分布:
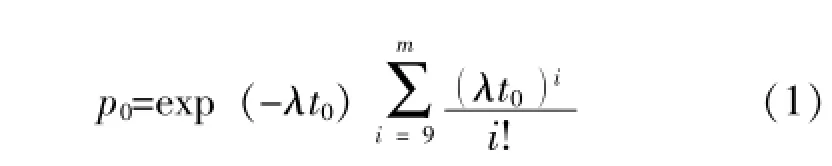
这是一个经典的模型。但人们在实践中发现用于实际的备件保障中过于保守。因而在20世纪80年代起美国军方使用 “后订货期望值”模型,这一模型在理论上是不严密的,也是与客观实际背离的。笔者在2009年导出了泊松分布的平均概率模型 [6]:
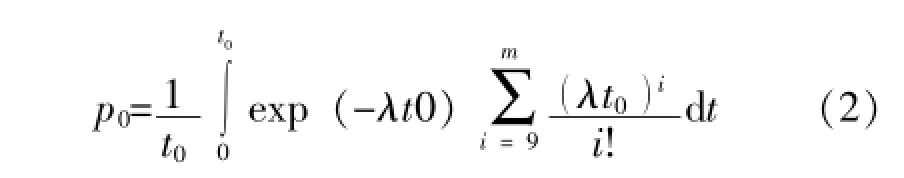
它真实地反映了客观实际。因为泊松分布的模型是反映保障期末时刻的备件保障概率,是保障期t0内保障概率最低的水平,在配置备件保障的起始时刻,备件保障无疑等于1,随着备件对象在t0时间内的逐个失效而备件随之减少,导致备件保障概率逐步地下降,直到期末的最低水平。因此,用最低水平来描述保障概率从最高水平逐步地降低到期末水平显然是过于保守的。用上述均值模型表达是合理的,据此进行的仿真试验也可以得到印证。
对于系统备件保障概率Ps的模型,符合客观实际的是不同更换模块失效概率的加权模型,适用于连续工作任务剖面的模型是:

适用于间断工作任务剖面的模型是:
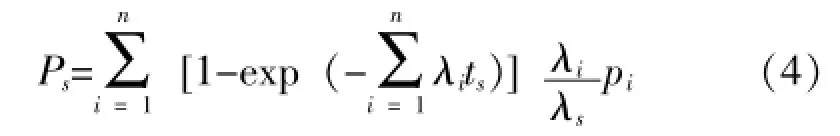
式 (3)中:n——组成系统的不同更换模块的数量;
pi——序号为i的更换模块的备件保障概率;
λi——序号为i的更换模块的失效率。
对于可修部件的备件保障概率,则可以使用泊松分布模型,只要把模型中的周转时间参数明确为失效部件检修复原的时间和故障件送修与修复件返加的双程的运输时间。因为这样的模型就符合备件保障的定义。
2 不同的备件保障供应体制与备件补充方式
为了进行备件优化配置设计,必须针对不同的实际需求,选择不同的备件供应体制和备件补充方式才能实现。
所谓备件供应体制,是指配置备件的站点设置,对此我们提出现场、备件供应站两站制,近距离库房、备件供应站两站制,现场、库房、备件供应站三站制,现场、中断站、备件供应站三站制4种基本体制。
备件补充方式指的是当站点的备件因替换故障模块而减少时如何补充备件的方式。我们提出3种补充方式,即定期补充方式、实时补充方式和定数补充方式。
定期补充方式是指当站点备件减少时,不要求即时补充,而是规定一个日历周期,每经历一个周期,对现场、库房和中断站一次性地补足备件到设计规定的配置数量。
实时补充方式是指当现场、库房和中继站规定配置的备件减少时,要求立即进行补充,但实际的实时补充是做不到的,因为备件供应站要加工制造(对消耗性部件)或检修复原 (对可修部件)时间,即使备件供应站有现成的备件,也要经历运输时间才能到达目的地。因此,实时补充方式实际上也要经历一定的周转时间。
定数补充是指各站点配置的备件减少到规定的数量后才要求补充备件,在要求的备件保障概率相同的条件下,它的备件数量比实时补充方式要多,而运输备件的次数要少。
这3种备件补充方式实际上是结合实际情况对备件配置费用和运输费用的权衡。
备件的优化配置设计实际上是战备完好率要求、维修保障设计、备件供应体制和备件补充方式密切关联的。它们的分析预计数学模型已经给出[7],此处不再一一列出。
但要实际运算,特别是进行优化配置设计,没有计算机辅助软件是困难的。
为此,我们开发了系列软件,备件配置的优化设计和分析才能顺利地实现。
下面我们通过一个虚拟的数值示例,考察备件优化设计的作用。
3 使用软件设计的数字示例
由100种类别239个现场更换模块组成的一个系统,每种更换模块的在线数和必须数 (必须数是指系统保持可靠的必要条件),各类模块单个单元的失效率和修复率如附录表中所示。设系统的备件系可修备件,故障部件的检修时间和双程运输时间合计均为2 190 h,即各种备件的周转时间均为2 190 h(软件允许设置不同的备件具有不同的周转时间)。设系统每次的任务持续工作为6 h,战时任务间隔停机时间为2 h。非战时值班或训练每天执行一次任务。设要求战备完好率不小于0.979 47。
采用现场、备件供应站两站点体制,备件补充方式采用实时补充方式
a)在战时体制下,软件输出的最优备件配置为:

备件总数为409件。
b)对于平时体制,软件输出的最优备件配置为:

备件总数为150件,是战时备件配置的36.57 %
c)对于同一基地,任务需要配置相同的4套系统,当处于战时状态,且4个系统同时工作,它的备件配置则为:

备件总数为820件。
备件总数为820,是单机备件的2倍,而非4倍。但如果4套系统不在同一基地,则每一个系统基地均需配置409件备件,4套系统备件总数才是单一系统的4倍。
在这种条件下,备件供应体制应该采用库房三站制,即现场备件配置为各套系统所用,库房备件则为4套系统公用。这比各自采用两站点体制要节省备件。
在上述条件下,并设库房到达各现场的时间距离为1 h,则由软件给出最佳配置。
a)现场备件的最佳配置为:

b)库房备件的最佳配置如下:

备件总数为1 337件,是4套系统单独采用两站点配置总数的81.72%。当同一系统的总套数增多,减少的备件数则更加显著。
当然,库房三站点要比两站点体制增加库房设施,则当套数较少时要作全面权衡。
对于中继三站制,更换模块划分为现场更换模块LRU和内场更换模块SRU,更换模块的主角由SUR承担;而SRU规模小于LRU,因此节省备件是必然的。以上述系统为例,100种LRU分解为265种SRU,平均1个LRU分解不到3个,就在此种条件下,4套系统的现场的LRU备件配置由软件输出。
a)现场LRU备件的最佳配置如下:

b)中继站备件的最佳配置如下:

备件总数等效LRU的备件数为673件,是库房三站制备件的50.33%,是两站制的41.13%。当然,中继三站制的中继站要配置检测、检修仪器和检修人员;但中继三站制不仅能减少备件,而且易以解决快速维修保障的问题。
对于近距离备件库房的两站制,即现场不配置备件,一旦失效发生而需要备件,就需等待备件从近距的库房中提取;当现场更换模块失效率过高,库房离现场时距时间过长,库房备件最多也不能满足战备完好率要求。但在国外商业软件中对此没有得到应有的反映。在我们的软件中,对此或者要求降低战备完好率要求,或者要求缩短库房离现场的时间距离,或者指明不适应此种备件供应体制。
上面仅就备件供应体制对备件配置的影响作了粗略的讨论,还有备件不同的补充方式对降低寿命周期费用的作用也有相当的回旋余地,总之,针对不同的实际环境,备件的优化设计具有深厚的潜力。限于篇幅,不能详细地阐述讨论。
当给出每种备件的购置费用、检修费用、存贮费用和运输费用的条件下,设计软件还可给出相应的使用周期的各种费用和总计费用。
附录:
100种现场更换模块的种类数、在线数、必须数、单个模块的失效率和修复率数据如表1所示。
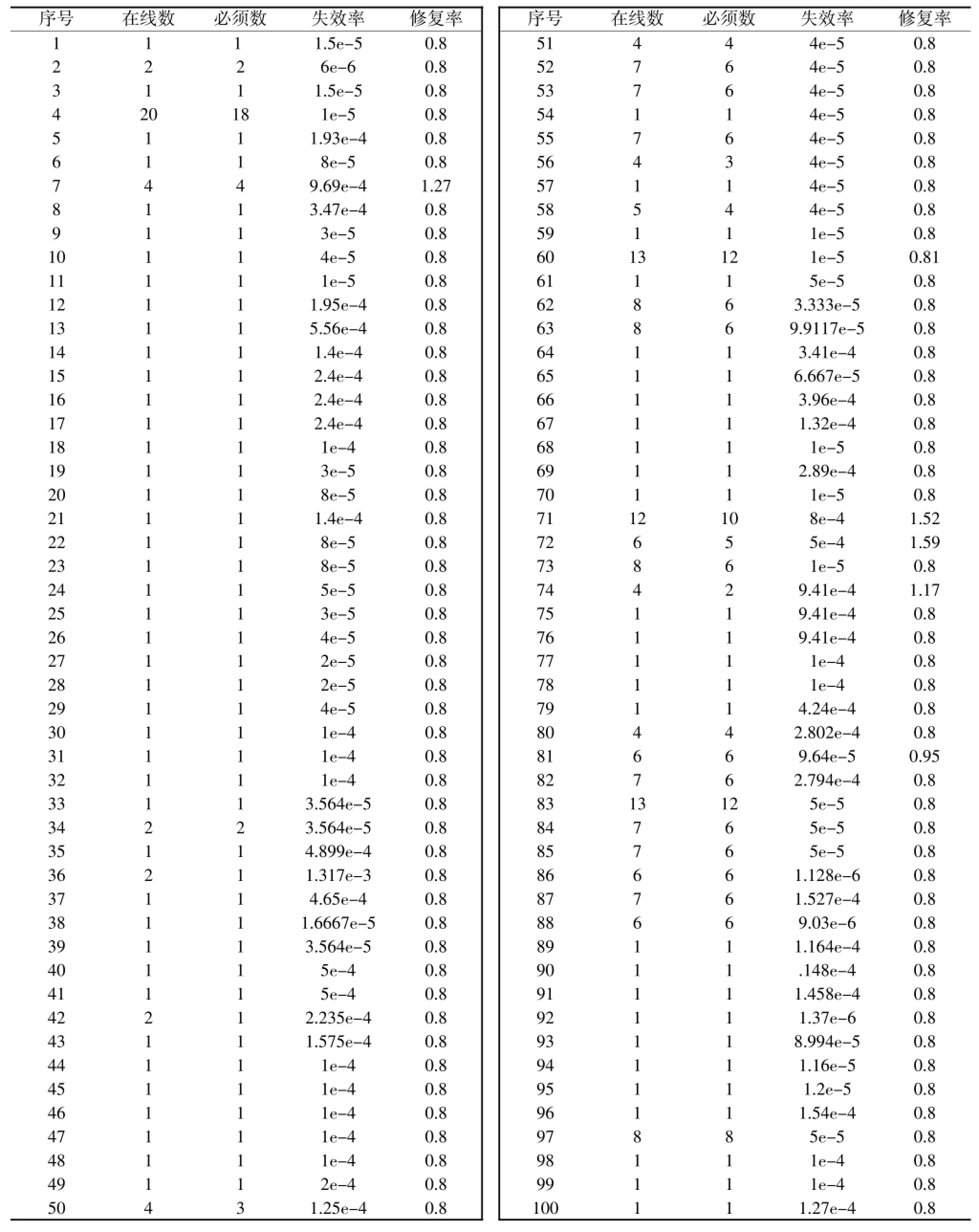
表1 100种现场更换模块的各种数据
4 结束语
运用备件优化设计分析软件,繁重艰巨的、复杂的设计任务可以快速、顺利地实现,说明所开发的备件优化设计模型的效果是卓越的。但同时必须注意,除了保证设计模型的正确性、通用性和优良性,还必须注意部件失效率的正确性。因此,积极积累现场失效数据,正确评估更换模块的失效率是非常重要的,正确的设计模型容易被不正确的失效误导。
为了加快发展备件保障设计的效益,笔者现阶段愿意无条件地义务服务,以推进备件的优化设计。联系电子信箱为:ddh_ddh@126.com
[1]丁定浩.新型战备完好率模型 [J].电子产品可靠性与环境试验,2010,28(3):1-5.
[2]丁定浩.可修备件保障概率的适用模型 [J].电子产品可靠性与环境试验,2013,31(2):1-4.
[3]丁定浩.战备完好率与使用可用度参数述评 [J].军用标准化,2012(2):40-43.
[4]GJB 4355-2002,备件供应规划 [S].
[5]HUMAR U D,et al.Reliability maintenance and logistic support:a life cycle approach [M].USA:K luwer Academic Publishers,2000:281-344.
[6]丁定浩.备件保障概率新模型 [J].中国电子科学研究院学报,2009(3):327-330.
[7]丁定浩,陆军.装备寿命周期使用保障的理论模型和设计技术 [M].北京:电子工业出版社,2011.
Optimal Design of the Configuration of Spare Parts
DING Ding-hao
(China Acaemy of Electronics and Information Technology of CETC,Beijing 100041,China)
So far there is no series of theory and design models for optimal design of sparesconfiguration in China and other countries.For current available foreign commercial software for spares support design,there is no any explanation for their theoretical basis,nor any published simulation models,and its correctness is hard to identify.In practical,the design is usually extremely conservative and unreasonable,far from optimal.For this reason,the corresponding optimal design software was developed, and its rationality and correctness can be dem onstrated w ith theoreticalm odels and sim u lations.
spare parts configuration;spares support;spares supply system;spares supplementway
TB 114.3
:A
:1672-5468(2015)01-0001-06
10.3969/j.issn.1672-5468.2015.01.001
2014-07-07
丁定浩 (1929-),男,江苏吴江人,中国电子科技集团公司电子科学研究院研究员,上海大学、南京航空航天大学兼职教授,长期从事系统可靠性、维修性、保障性理论和工程设计研究工作。
