基于小波分析的主动预警式网络信息安全运维

林征，李洋

（中国移动通信集团贵州有限公司贵阳分公司，贵州 贵阳 550001）

基于小波分析的主动预警式网络信息安全运维

林征，李洋

（中国移动通信集团贵州有限公司贵阳分公司，贵州 贵阳 550001）

提出了一种基于小波分析的安全运维分析方法，在海量数据挖掘的基础上，利用小波分析理论对数据进行分析，提出针对海量数据的波形化、波形的降噪方法以及小波函数二进制离散算法等问题的解决方案，实现对未来的安全趋势进行主动预警，从而提高网络与信息安全工作效率。

小波分析 主动预警 信息安全 安全运维

1 传统网络与信息安全工作开展模式分析

近年来，网络运营商在信息安全体系基本建设完成后，仍旧在网络与信息安全运维管理过程中面对不断出现的新问题和信息安全管理短板。日常网络与信息安全工作繁杂（包括日常漏洞整改加固、未备案网站核查、垃圾短信治理、日志分析、设备巡检等多项常态化工作），且人员配置及技术储备相对薄弱，导致大部分网络与信息安全工作只得被动展开，缺乏预警机制，从而无法及时对安全运维过程中暴露的安全问题进行分析和评价。

传统网络与信息安全工作开展的技术性问题主要包括如下：

（1）网络安全工具或者监控系统使用复杂，工作难度大。

（2）对于网元设备、服务器设备、网络安全设备产生的日志没有技术手段进行有效分析，难以有效利用海量数据资源。

（3）安全预警和处理多靠人员经验，无成熟的理论和工具。

（4）安全维护工作成果无法用数字或图表的形式直观展现，很难得到认可。

传统网络与信息安全工作开展的管理性问题主要包括如下：

（1）制度或流程未能有效地贯彻和落实。

（2）管理措施被抛弃或故意绕过。

（3）安全管理制度与其他制度存在冲突。

（4）内部人员对落实体系的积极性不高，缺乏主观能动性。

（5）缺少长远规划，没有突出重点问题。

对于日常运维管理工作中的技术性问题，需要一种适用的网络安全工具：这种工具有足够先进和精确的理论支持；可对现有运维数据进行深度挖掘；可以及时地对将可能要发生的安全事件进行预警；可以为安全运维工作提供短期和长期的方向性指引；可以表达安全运维工作的成效，为决策管理层提供数据支持。

2 小波理论原理

小波分析理论最早是由法国数学家Molet在1980年进行地震数据分析工作的过程中提出，随后S.Mallat在1989年提出多分辨率分析的概念，统一了其他人提出的各种具体小波构造方法，给出了Mallat算法。小波变换作为替换短时傅里叶变换的一种方法被提出来。小波分析与短时傅里叶分析采用相同的处理方法，也是用窗口的形式将一个函数与信号相乘（小波变换中这个用来相乘的函数就是小波函数），变换结果被分成在时域内不同的片段。尽管如此，连续小波变换与短时傅里叶变换还是有2个主要的不同点：

（1）由于傅里叶变换没有采用加窗的方式，会在变换结果中看到相应正弦信号的尖峰，因此结果中没有负频率。

（2）为计算每个单一的频谱分量，需要将窗口宽度改变，这可能是小波变换最重要的特征。

连续小波变换定义为：

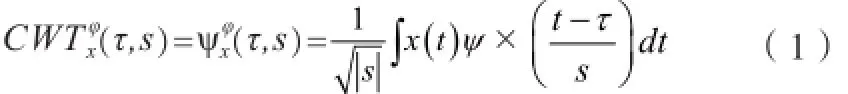
小波变换其实是一个含有2个自变量的函数（t和s），分别作为平移和缩放参数。psi(t)是变换函数，称之为母小波。满足这个条件的窗函数应该是有限宽度的，且函数是振荡的。“母”这个字眼揭示了变换中用到的含有不同支撑域的函数，都可以追溯到一个主要函数——母小波。换句话说，母小波就是产生其他窗函数的原型。

“变换”这个词和在快速傅里叶变换中的变换是一样应用的。随着窗口在信号上平移，和窗口的位置相关。这个说法在变换域内明显反映了时间信息。不过，不像之前说的短时傅里叶变换，没有频率参数，而以frequency的缩放参数将其取代。

小波分析克服了工程界一直应用的傅里叶变换不能同时具有时域和频域的细节特征，通过小波基的伸缩和平移，根据信号的变换特征自适应地调整分析方式，更准确地捕捉到众多离散数据中的突变信号。

3 基于小波理论的主动预警式网络信息安全运维内容

在网络信息安全运维工作中会接触大量的数据，包括实时网络流量日志、防火墙产生的连接数日志、操作系统和网元的告警日志、网络入侵检测系统产生的入侵告警、审计系统产生的操作审计日志信息、日常检查出的漏洞分布情况、检查操作系统配置合规情况等，随着网络安全和信息技术的发展，将会接触到更多的系统，且面对更海量的数据。因此，有必要对这些数据进行深度挖掘分析，从而找出隐藏信息和规律，甚至可以提前对网络安全情况进行预警，对未来的网络安全走势进行预测，从而指引日常信息安全运维工作的方向。

以上的海量日志数据都有一个共同的特征——时序。需关心这些日志数据的时间维度，比如：异常流量发生的时间、安全漏洞发生的时间、系统入侵的时间、系统告警的时间等。

传统的分析挖掘方法一般是基于统计学，将时间序列数据作为变量来处理。但是如果换一个角度，可以把海量日志数据从时间和发生频率这2个维度考虑，将所有日志数据看做是波形，即可以采用小波分析原理对日志数据进行处理，从小波分析的结果来提升日常安全运维。

若要将小波理论在主动预警式的网络分析系统中进行实现，还需要克服以下3个问题：

（1）对现有在运维过程中得到的海量日志数据进行数模转换，对数据进行波形化。

（2）对得到的波形进行去噪。

（3）对小波变换函数进行二进制离散化。

在克服这些困难之后，可以依照图1所示的顺序进行数据的输入/输出：

图1 小波理论主动预警系统演进图

（1）通过对安全事件进行分析，确定与安全事件密切相关的属性（如漏洞信息、流量信息、攻击信息、时间信息、发生频率、危害程度等）。

（2）设计数据采集模块，对安全防护设备、网络设备、主机系统进行数据采集。

（3）对采集到的数据进行量化，得到一系列的数值型数据。同时，把离散的数值数据转换成波形，即把数字信号转换成模拟信号，以进行小波分析。

（4）数据采集过程中由于外界因素的影响或检测误差的存在，采集到的数据通常都包含噪声，用小波变换做降噪处理，使信号能最大限度地反映原信号本身的规律与性质。

（5）对处理过的信号波形运用小波分析，检测出频率突变点的位置。

（6）综合各个属性的检测分析结果，对影响公司日常安全运维的风险因素进行预警，评价公司网络与信息安全工作开展整体情况及整体安全水平，为安全策略的制定提供依据。

3.1 日志数据的波形化

日常运维过程中产生的日志数据往往都会对应某时刻或者某段时间内的情况。如果将一种情况的值，比如网络流量大小或者检查出的漏洞数目、检测到的网络攻击数目等按照一定方法量化后作为波形的幅度si，和其对应的时间值ti，则会形成一组离散化的波形，带入到公式为x(t)={ti,si}，那么所有类型的情况的值都可以是这样一组波形，从而实现了日志数据的波形化。

3.2 波形的去噪

在得到日志数据波形化后难免会出现噪声，为了更加准确地分析波形，需要进行去噪。从实践结果来看，噪声和有用信息的细节部分一般都会在波形的高频区域，传统的傅里叶变换无法去除噪声和有用信息重叠区域特别大的情况。因此，可采用小波分析的方法来去除噪声，这样更能保持去噪过程中波形细节不受损失。

有用信号的小波系数往往幅度大、数目少，而噪声信号的小波系数则幅度小、数目多，因此可先设定一个阈值，在阈值内的为有用信息，在阈值之外的认定为噪声。

在小波函数满足容许条件的情况下，可以用傅里叶变换经过阈值处理后的小波分解结果来重建原始波形，便于在降噪之后对优化后的波形进行进一步分析。

小波容许条件为：

其中，Ψ(ω)为小波函数的傅里叶变换。

通过这样的小波变换，可以对原有的波形进行有效降噪，过滤掉无用的日志数据信息，从而为后续的精确预警提供了基础。

3.3 二进制离散化

为了实现对日志数据的周期性分析和安全预警，需要对函数进行二进制离散，这样可以通过计算机程序来利用小波变换函数对被数模化的大数据进行多级分解，从而实现对网络攻击的提前预警并提供预见性指引。

如果：

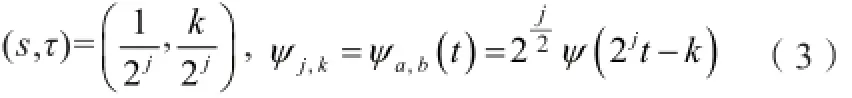
那么，x(t)可以表示的小波序列为：

其中：

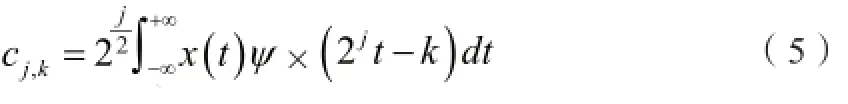
在日志数据二进制离散后，实现对日志数据大规模多级分解，并且进行周期性规律分析，从中发现异常信息，提前预警，从而为日常安全运维工作提供主动式的思考，让日常安全运维工作更加有序开展，提升日常安全运维水平。

4 实践效果

该理论在笔者单位安全运维方面得到了应用，效果显著。2013年该理论实践后变换得到的日常安全运维趋势如图2所示：

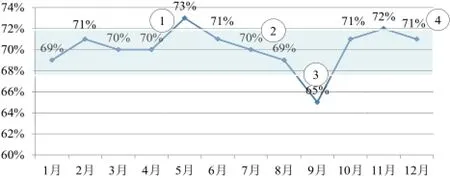
图2 小波理论主动预警系统日常安全运维趋势图

（1）点1：73%异常，超出了笔者认为的68%和72%的控制区间。

（2）点2：69%，这个指标是在笔者的受控区间中，但仍然是异常。

（3）点3：65%，低于阈值，异常。

（4）点4：71%，这个也是异常，是连续3个点（71%、72%、71%）落在控制中线（70%）的一侧，显示可能出现了单边安全形势。

在2013年内，通过该系统笔者单位运维安全预警明显得以提升，及时发现网络异常事件11起，整治网络安全漏洞43个，同比2012年笔者公司投入运维安全人员由2 104人/时降至733人/时，可有效控制网络风险，大幅提升工作效率。

5 结束语

通过小波变换分析手段，可以将在工作中收集的海量网络和信息安全有关数据进行深度挖掘分析，并且建立基于小波理论的主动预警式网络分析理论和系统，将数据收集、数据数模转换、数据降噪、数据分析等过程全自动化、图形化表现出来，对网络安全各事件的发生进行规律解读，提前预警可能发生的风险事件，使日常信息安全运维工作有理可依、有据可循，为从以事件为导向的被动型安全企业转变为以风险为导向的成熟型安全企业提供有力的技术支撑。

[1] ROBI POLIKAR. THE ENGINEER’S ULTIMATE GUIDE TO WAVELET ANALYSIS: The Wavelet Tutorial[EB/OL]. (2012-02-16). http://yanlijun250.iteye. com/blog/1418011.

[2] Lokenath Debnath. Wavelet Transforms and Their Applications to Turbulence[EB/OL]. (2011-05-25). http:// wenku.baidu.com/link?url=ZC1JSaTZsrc1P9yl6BEDC-rh_3 VkQOVRJeW3Jn2BzVYyzQhiuPd0V0WtbrKqOJi35MEIR QhJmnYqiGVLO_L3eQmaTjIVinygV9SOMVPrCye.

[3] Daubechies I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis[J]. IEEE Transactions on Information Theory, 1990,36(5): 961-1005.

[4] Mallat S. A Theory for Multiresolution Signal Decomposition[EB/OL]. (2010-11-26). http://wenku. baidu.com/link?url=gxrUf621vw9fIoHyze5Gk53z16W6 6vNO7IcCPJATzZhtQpnhORiQ6-SnyidmWb18Szvdpv_ Ckn66OK7yHhsogBcETAq9wtgIEzfQcTTMKaq.

[5] 李世雄. 小波变换及其应用[M]. 北京: 高等教育出版社, 1997.

[6] 何岭松. 小波函数性质及其对小波分析结果的影响[J]. 振动工程学报, 2000(1): 143-146.

[7] 刘素一,权先璋,张勇传. 不同小波函数对径流分析结果的影响[J]. 水电能源科学, 2003(1): 29-31.

[8] 段瑞玲,李玉和,李庆祥. 小波函数的选择及其对图像滤波性能影响[J]. 计算机应用, 2005(12): 219-220.

[9] 张平文,刘法启. 小波函数值的计算[J]. 计算数学, 1995(2): 173-185.

[10] 张新红. 小波网络理论及其在经济预测中的应用研究[D]. 天津: 天津大学, 2003.★

Active Warning Network Information Security Operation Based on Wavelet Analysis

LIN Zheng, LI Yang
(China Mobile Group Guizhou Co., Ltd., Guiyang Branch, Guiyang 550001, China)

A security operation and maintenance evaluation method based on wavelet analysis was presented in this paper. Based on huge amounts of data mining, data was analyzed by means of wavelet analysis theory. A noise reduction method according to wave form of huge amounts of data was presented. Also, a solution to binary discrete algorithm of wavelet function was put forward to achieve active warning to future security trend and enhance effi ciency of network and information security.

wavelet analysis active warning information security security operation

10.3969/j.issn.1006-1010.2015.12.011

TP319

A

1006-1010(2015)12-0054-04

林征,李洋. 基于小波分析的主动预警式网络信息安全运维[J]. 移动通信, 2015,39(12): 54-57.

2015-04-28

责任编辑：袁婷 yuanting@mbcom.cn