随机粗糙海面的建模与仿真

【基础理论与应用研究】

随机粗糙海面的建模与仿真

温东阳,察豪,孟路稳

(海军工程大学 海洋电磁环境研究所,武汉430033)

摘要：针对海浪运动的随机性，通过采用蒙特卡洛方法和分形法对随机海面进行了模拟，用Matlab软件模拟出较为理想的结果,并通过分析参数变化引起的海面形状变化作了分析，得出有益于模型优化的结论。

关键词:蒙特卡洛法；分形法；海面模拟

收稿日期：2014-07-28

作者简介：温东阳(1988—)，男，硕士，主要从事信息科学与控制工程研究。

doi:10.11809/scbgxb2015.01.040

中图分类号：TN954

文章编号：1006-0707(2015)01-0145-03

本文引用格式：温东阳,察豪,孟路稳.随机粗糙海面的建模与仿真[J].四川兵工学报，2015(1):145-147.

Citationformat:WENDong-yang,CHAHao,MENGLu-wen.ModelingandSimulationofRandomRoughSea[J].JournalofSichuanOrdnance,2015(1):145-147.

ModelingandSimulationofRandomRoughSea

WENDong-yang,CHAHao,MENGLu-wen

(InstituteofOceanElectromagneticEnvironment,NavalUniversityofEngineeringofPLA,Wuhan430033,China)

Abstract:In view of the random wave motion, we simulated the random sea by using the monte carlo method and fractal method, and simulated the ideal results with the Matlab software. And the analysis of the sea surface shape change caused by the parameter changes was analyzed. The result we got is beneficial to model optimizing.

Keywords:montecarlomethod;fractalmethod;surfacesimulation

随着海洋科学的发展，人们对海洋的研究日益深入。海浪的研究对国民生产、国防中的许多问题具有实际意义，尤其在模拟海面电磁散射过程中，建立合适的海面模型具有关键的作用。海面是不规则的随机粗糙面，一般采用2种方法模拟海面；一种是基于统计模型，并采用蒙特卡洛方法进行海面模拟。另一种是采用分形模型模拟海面，同时可以描述海面的统计特性和随机特性。无论哪种方法都可以比较真实反映海面的真实情况。建立符合实际的模拟海面对后续研究具有重要意义。

1粗糙海面的蒙卡洛模型

1.1一维粗糙海面

由于粗糙海面被认为是由大量的谐波叠加而成，谐波的振幅是独立的高斯随机变量，其方差正比于特定波数的功率谱S(kj)。按照这种思路，可以由下列函数生成长度为L的一维粗糙表面样本[1]，即

(1)

其中:xn=nΔx(n=-N/2+1,…,N/2),表示粗糙表面上第n个采样点; F(kj)与f(xn)称为Fourier变换对，定义为

(2)

其中:定义离散波数kj的表达式为kj=2πj/L;Δk定义为谱域相邻的谐波样本的空间波数差;S(kj)为粗糙海面的功率谱密度;N(0,1)表示均值为0，方差为1的正态分布的随机数。

1.2二维粗糙海面

假设要产生的二维随机粗糙面在x和y方向的长度分别为Lx和Ly，等间隔离散点数为M和N，相邻两点间的距离分别为Δx和Δy，有Lx≈N·Δx, Ly≈N·Δy,则粗糙面上每一点(xm=mΔx, yn=nΔy), (m=-M/2+1,…,M/2; n=-N/2+1,…,N/2)处的高度可表示为

(3)

式中

学校要转变教学观念。学校要端正办学思想，真正树立素质教育的观念，重视学生的心理健康问题，把心理健康教育真正作为素质教育的重要组成部分摆在学校教育的重要地位。建立和完善心理咨询和教育体系，坚持以学生自我调适为主，教师辅导为辅，重点医治的方针，采用多种方式方法，开展丰富多彩的活动，普及心理健康教育，从而提高学生的心理素质。

F(kmk,knk)=2π[LxLyS(kmk,knk]1/2·

(4)

同样S(kx,ky)为二维粗糙海面的功率谱密度，其中kmk=2πmk/Lx，knk=2πnk/Ly。在具体计算式(4)通常是利用二维IFFT来实现的，二维海面模型如图1所示。

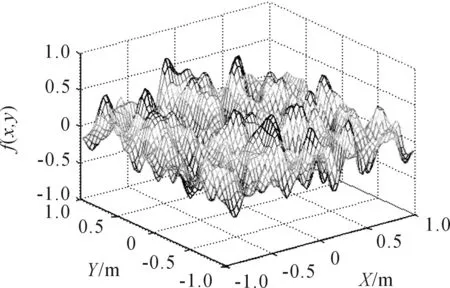
图1　二维海面模型

2粗糙海面的分形模型

“分形”的概念是由Mandelbrot[2,3]首次提出的，分形指的是组成部分与整体以某种方式相似形，分形表征的是形体内部嵌套的自相似结构。所谓自相似，简单地讲就是缩放对称性，是指研究对象在所有方向按同一比例扩展或收缩的均匀线性变换。

2.1一维分形海面模型

基于带限Weierstrass分形函数的一维经典动态分形海面模型的表达式为[4]

(5)

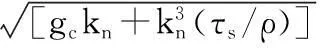
(6)

(7)

归一化因子为

(8)

构建的一维分形海面模型如图2、图3所示。

图2　当分维数D=2.1时的一维随机海面模型

图3　当分维数D=2.5时的一维随机海面模型

2.2二维改进分形海面模型

经典的二维Weierstrass分形海面模型表达式为[6,7]

(y+Vyt)sinβn]-ωnt+Φn}

(9)

经典二维分形海面模型只能较好地模拟粗糙海面功率谱的负幂律部分，但是由于二维海面的功率谱并不是单纯的负幂律谱，而是当空间波数大于基波波数时海面的功率谱函数近似是负幂律函数，当空间波数小于基波波数时，海面的功率谱函数近似满足正幂律函数关系，因此与改进的一维分形海面模型类似，改进二维分形海面模型如下

(y+Vyt)sinβm]-ωmt+Φm}+δη×

(y+Vyt)sinφn]-ωnt+Φn}

(10)

其中:a是空间波数小于基波波数时的尺度因子;b为空间波数大于基波波数时的尺度因子;βm和φn为波浪的运动方向角;ωm和ωn是角频率;Φm和Φn是[-π,π]上均匀分布的随机相位。一般来说式(10)中的βm和φn是时间的函数，在较短时间内可以简单的认为是和时间无关。 构建的不同参数情况的二维改进分形海面如图4～图7所示。

图4风速U19.5=5m/s，风向β0=0°，分维数D=2.1时的二维改进分形海面

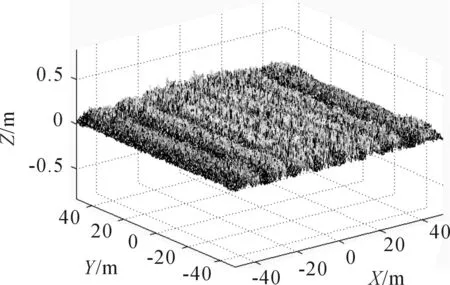
图5风速U19.5=8m/s，风向β0=0，分维数D=2.1时的二维改进分形海面

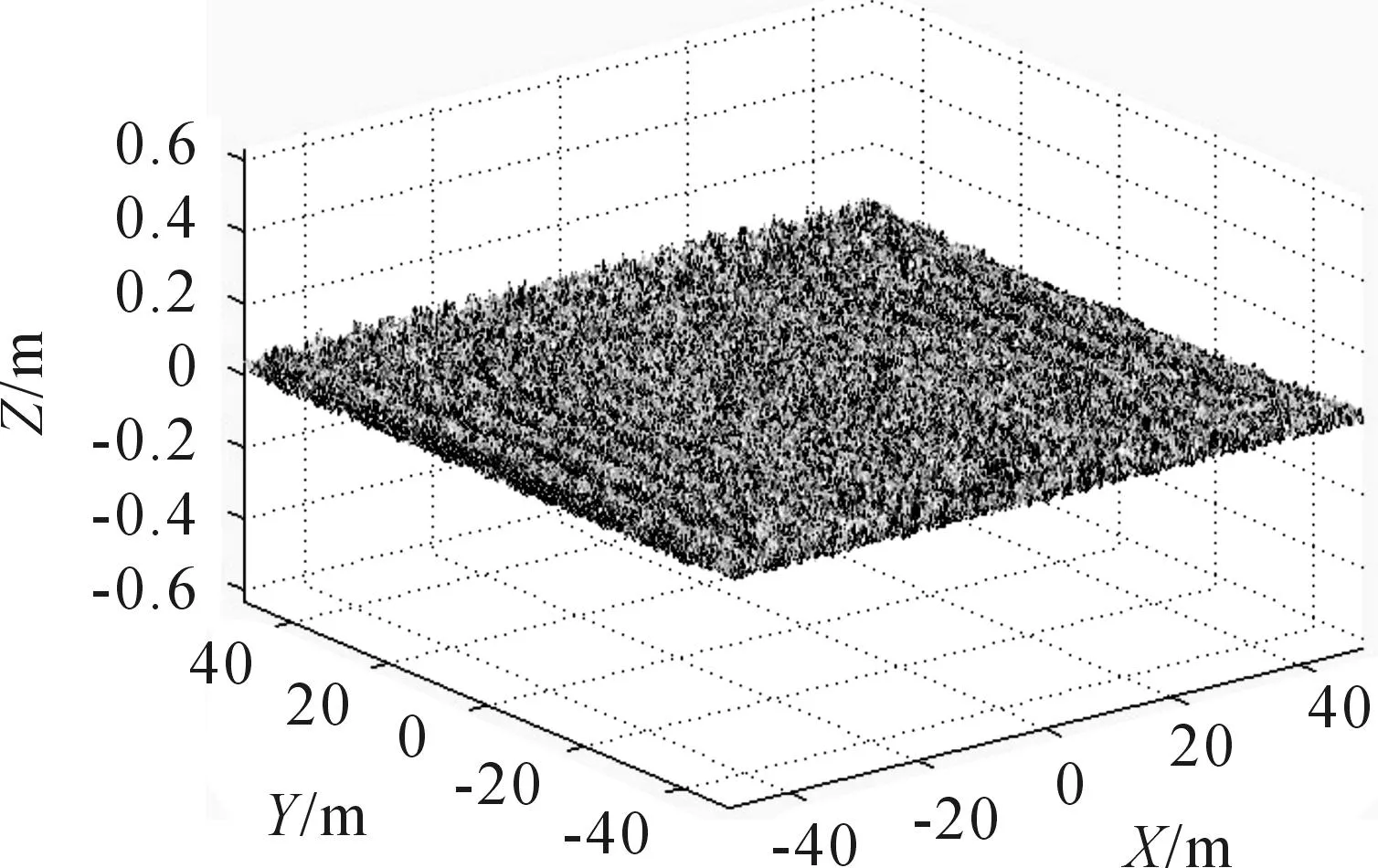
图6　风速U 19.5=5 m/ s，风向β 0=0，分维数D=2.5时的二维改进分形海面

3结束语

从以上分析与仿真来看，2种模拟海面的方法都可以反映海面的随机特性，且比较符合海面实际情况。所建模型为以后海面建模、电磁散射以及海上目标的分析与研究提供了支持。

参考文献:

[1]ThorsosEI.ThevalidityoftheKirchhoffapproximationforroughsurfacescatteringusingaGaussianroughnessspectrum[J].J.Acoust.Soc.Am，1988，83(1)：78-92.

[2]BerizziF，MeseED,PinelliG.One-dimensionalfractalmodeloftheseasurface[J].IEEEProc.RadarSonarNaving.1999，146(1)：55-64.

[3]HarrisonGP，WallaceAR.Climatesensitivityofmarineenergy[J].RenewableEnergy，2005，30(12)：1801-1817.

[4]BerizziF，MeseED，PinelliG.Atwo-dimensionalfractalmodeloftheseasurfaceandseaspectrumevaluation.ProceedingsofRadarSystems[J].Radar97，1997，1(449)：189-193.

[5]BerizziF，MeseED，MartoreliaM.Aseasurfacefractalmodelforoceanremotesensing[J].Int.J.RemoteSensing，2003，25(8)：1265-1270.

[6]王运华，郭立新，吴振森.改进的二维分形模型在海面电磁散射中的应用[J].物理学报，2006，55(10)：209-217.

[7]GuoLixin，WuZhensen.Fractalmodelandelectromagneticscatteringfromtime-varyingseasurface[J].ElectronicsLetters，2000，36(21)：1810-1812.

[8]熊艳飞，石志广，郭建，等． 基于海浪谱模型和FFT的海面建模[J]．重庆理工大学学报: 自然科学版， 2014 ( 4):77-82．

(责任编辑蒲东)