改进最短路方法在军用油料运输中的应用
2015-12-23苏涛,郝梦媛
【后勤保障与装备管理】
改进最短路方法在军用油料运输中的应用
苏涛,郝梦媛
(1.海军航空工程学院 控制工程系,山东 烟台264001;
2.烟台大学 信息与计算科学,山东 烟台264000)
摘要:针对油料运输面临的风险因素很多,事故损失较为严重,安全问题突出的问题。选择合适的运输路径是提高油料运输安全的重要途径。用改进的最短路方法求解最安全路线的问题,事故风险最小,确保了油料运输的安全。
关键词:油料运输;最短路;安全路线
收稿日期:2014-07-29
作者简介:苏涛(1979—),男,硕士,讲师,主要从事军事物流信息化研究。
doi:10.11809/scbgxb2015.01.022
中图分类号:O221.3
文章编号:1006-0707(2015)01-0078-03
本文引用格式:苏涛,郝梦媛.改进最短路方法在军用油料运输中的应用[J].四川兵工学报,2015(1):78-80.
Citationformat:SUTao,HAOMeng-yuan.ApplicationofImprovedShortestPathMethodinMilitaryOilTransportation[J].JournalofSichuanOrdnance,2015(1):78-80.
ApplicationofImprovedShortestPathMethodin
MilitaryOilTransportation
SUTao1, HAO Meng-yuan2
(1.DepartmentofControlEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China;
2.DepartmentofInformationandComputationalScience,YantaiUniversity,Yantai264000,China)
Abstract:There are many risk factors in oil transportation, such as facing more serious loss, accident, and safety problem. Choosing a right transportation route is an important way to improve the transportation safety. We got the maximum security route with the improved shortest path method to ensure the security of oil transportation.
Keywords:oiltransportation;shortestpathmethod;saferoute
作为一类危险品,军用油料的运输不同于一般军用物资运输[1]。由于其自身的理化性能,军用油料在运输过程中很容易发生泄漏、着火、爆炸等灾害事故,造成油料大量损失,产生极为严重的后果,因此对运输的安全要求较高[2]。相较于普通物资运输路径选择时更为注重对时间最少、路径最短等目标考虑,军用油料在选择运输路径时,更注重总的事故风险最小,防止油料运输损失,确保油料数量安全[3]。
最短路问题优化即在一个连通网络中,求从某一指定的节点(始点)到另一个指定的节点(终点)的一条路,使其路的长度最短[4]。用最短路问题解法求解最安全路线,则要求一条安全通过概率最高的道路,这时需要对问题做一些数学处理,即改进的最短路解法[5]。
1最短路算法
求解最短路的算法较多,如狄克斯拉(Dijkstra)算法、福劳德(Floyd)算法、逐次逼近算法等,下面给出常用的狄克斯拉算法[6]。
狄克斯拉算法的基本思想基于如下事实:若路P=(vs,v1,v2,…,vi,…,vn,vt)是vs到vt的最短路,则路P=(vs,v1,v2,…,vi)是vs到vi的最短路[7]。
狄克斯拉算法是一种标号法,它的基本思路是从起点vs出发,逐步向外寻找最短路。在寻找的过程中,给每一个顶点vj进行标号(λj,lj)[8]。其中,λj表示获得此标号的前一个顶点的下标,lj表示从起点vs到该点vj的最短路的权(称为固定标号,记为P标号)或表示从起点vs到该点vj的最短路的权的上界(称为临时标号,记为T标号)[9]。
算法开始时除vs外对所有顶点进行T标号,算法每进行一步都把一个顶点的T标号改为P标号,当终点vt得到P标号后,计算过程停止[10]。Si表示在第i步已具有P标号点的集合。若图中有n个顶点,则最多进行(n-1)次标号就求得从vs到vt的最短路。再根据每个点标号的第一个数λj反向追踪找出最短路径,计算步骤如下[11]。

2) 若Si=V,则算法终止,此时对任vj∈Si,lj=P(vj);否则转下一步[11]。

2改进的最短路算法
当把指标参数看成是通过每段道路的成功概率时,则可用最短路问题解法求解选择最安全路线的问题。不过,这时需要对问题做一些数学处理。
为说明这点,设vi、vj表示任一条道路两端的顶点,从vi到vj的安全通过概率为pij。由于一条路线是多条道路的串接,由概率论知,一条路线的安全通过概率应等于组成该路线的各条道路安全通过概率的乘积。例如,若把v1→v4→v5v6这条路线记为π,则有
P(π)=p14p45p56
(1)
应用最短路问题解决,需要使沿路线的指标参数等于各组成道路指标参数的和。对式(1)两边取对数并乘以负号,得
-lgP(π)=-lgp14-lgp45-lgp56
(2)
由对数函数特性知,使P(π)最大,等价于-lgP(π)最小,也就是使式(2)右边诸项和最小。所以,如果以-lgpij作为每条道路的指标参数,那就可用最短路问题解法求解了。
3实例求解
某航材油料的运输路线如图1所示,在图1中标示的各条道路安全通过概率下,用改进的最短路方法求v1到v6的最安全路线。

图1 运输路线

2) 考察与v1相邻的点v2、v4。因(v1,v2)∈A,v2∉S0,故把v2的临时标号修改为


同理得

v2、v4的标号分别为(1,0)、(1,-lg0.95),其余点的标号不变。

i=1:
3) v2为刚获得P标号的点。考查与v2相邻的点v3、v4。因为(v2,v3)∈A,v3∉S1,故把v3的临时标号修改为


同理得


v3、v4的标号分别为(2,-lg0.9),(2,0),其余点的标号不变。

i=2:
4) v4为刚获得P标号的点。考查与v4相邻的点v3、v5。因为(v4,v3)∈A,v3∉S2,故把v3的临时标号修改为


同理得


v3、v5的标号分别为(4,-lg0.9),(4,-lg0.95),其余点的标号不变。

i=3:
5) v5为刚获得P标号的点。考查与v5相邻的点v3、v6。因为(v5,v3)∈A,v3∉S3,故把v3的临时标号修改为


同理得
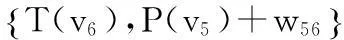

v3、v6的标号分别为(5,-lg0.9),(5,-lg0.76)。

i=4:
6) v3为刚获得P标号的点。v6与v3相邻,因为(v3,v6)∈A,v6∉S4,故把v6的临时标号修改为



i=5:
7) v6为刚获得P标号的点。因没有与v6相邻的点,算法终止。这样就得到了最优解,根据终点v6的标号可知(5,-lg0.76) 从v1到v6的距离是-lg0.76,其最短路径中v6的前面一点是v5,从v5的标号(4,-lg0.95)可知v5的前面一点是v4,从v4的标号(2,0)可知v4的前面一点是v2,从v2的标号(1,0)可知v2的前面一点是v1,即此最短路径为v1→v2→v4→v5→v6,其安全通过的概率为P(π)=1.0×1.0×0.95×0.80=0.76。
4结束语
改进的最短路算法巧妙地解决了求解最安全路线的问题,最大程度地保障了航材运输的安全。该算法不仅可以用来解决军用油料运输路线问题,对于其他领域的危险品运输也同样适用,且有很强的实用性。
参考文献:
[1]王铁宁.装备管理信息系统原理与应用[M].北京:国防工业出版社,2013.
[2]郭文晖.军事装备管理创新[M].北京:国防工业出版社,2010.
[3]赵经成,祝华远,王文秀.航空装备技术保障运筹分析[M].北京:国防工业出版社,2010.
[4]张丽叶.装备更新经济性分析[J].装备学院学报,2012,23(5): 36-39.
[5]WayneL.Winston.Operationsresearch[M].北京:清华大学出版社,2011.
[6]李维铮,甘应爱,田丰.运筹学[M].北京:清华大学出版社,2005.
[7]傅清祥,王晓东.算法与数据结构[M].北京:电子工业出版社,1998.
[8]DreyfusSE,LawAM.TheartandtheoryofDynamicProgramming[M].AcademicPress, 1977.
[9]马仲蕃,魏权龄,赖炎连.数学规划讲义[M].北京:中国人民大学出版社,1981.
[10]俞玉森.数学规划的原理和方法[M].武汉:华中工学院出版社,1985.
[11]王晓迪.高等学校教育装备管理决策支持研究[D]. 哈尔滨:哈尔滨工程大学,2011.
[12]沈贵林.基于动态规划的物流装备更新决策方法[J].物流科技,2006,29(12): 74-76.
[13]杨媛媛.装备更新决策综合方法[J].装备指挥技术学院学报,2002,13(4): 25-28.
[14]陈庆华.装备运筹学[M].北京:国防工业出版社,2005.
(责任编辑周江川)
