基于快速二阶滑模的超音速靶弹控制器设计

【装备理论与装备技术】

基于快速二阶滑模的超音速靶弹控制器设计

杨茂林

(江苏自动化研究所，江苏 连云港222061)

摘要：针对带有外界干扰和建模不确定性的靶弹姿态运动模型，结合快速二阶滑模和反演控制，设计了一种新的超音速靶弹反演滑模控制器；反演设计分步采用快速二阶滑模控制补偿外界干扰和建模不确定性，并利用Lyapunov稳定性理论证明控制系统稳定；采用滑模观测器对不确定性进行估计，解决了计算膨胀的问题；仿真表明：所设计控制器不仅能在有外界干扰和建模不确定性的情况下快速、准确地跟踪姿态角指令，还解决了舵偏角高频抖振的问题。

关键词：超音速靶弹；快速二阶滑模控制；反演控制；不确定性；抖振

收稿日期：2015-03-17

作者简介：杨茂林(1981—)，男，工程师，主要从事指火控系统研究。

doi:10.11809/scbgxb2015.06.009

中图分类号：TP273

文章编号：1006-0707(2015)06-0033-05

本文引用格式：杨茂林.基于快速二阶滑模的超音速靶弹控制器设计[J].四川兵工学报，2015(6):33-37.

Citationformat:YANGMao-lin.FastSecond-OrderSlidingModeControllerDesignfortheSupersonicTargetMissile[J].JournalofSichuanOrdnance,2015(6):33-37.

FastSecond-OrderSlidingModeControllerDesignfor

theSupersonicTargetMissile

YANGMao-lin

(JiangsuAutomationResearchInstitute,Lianyungang222061,China)

Abstract:Aiming at the target missile attitude motion model with external interference and modeling uncertainties, a fast second-order sliding mode inversion controller was proposed for the system. Fast second-order sliding mode control was compensated of external interference and modeling uncertainties in backstepping control. Lyapunov stability theory was used to prove that the control system is stable. High order sliding mode observer was used to estimate uncertainty and solve the problem of calculating the expansion. Simulation results show that the designed controller can not only track attitude angle command fast and accurately, also address the rudder angle chattering problem.

Keywords:supersonictargetmissile;fastsecond-orderslidingmodecontrol;backsteppingcontrol;uncertainty;chattering

为了应对世界各国反舰导弹特别是超音速反舰导弹的飞速发展，研发单位研发了新一代舰载防空反导系统。为了检验防空反导系统的性能，用靶弹模拟反舰导弹来进行试验评估。超音速靶弹主要模拟反舰导弹的末端飞行特性。根据超音速靶弹飞行特性建立的模型是非线性的且具有较大的不确定性，且靶弹飞行速度快，控制系统难以快速响应。因此，应寻找鲁棒性强、响应迅速的控制方法来控制靶弹。

滑模控制目前是比较流行的控制非线性系统的方法，其简单易懂，在控制有较大不确定性的系统时鲁棒性好，但是存在抖振的现象。文献[1]通过终端滑模与反演结合，设计导弹的反演滑模控制器，使跟踪误差收敛，并防止了舵片抖振。文献[2]估计系统不确定性和扰动的大小，设计了拦截系统的一个二阶滑模制导率，该制导率能够保证快速的视线角的收敛。文献[3]针对混合了时滞、随机出现的不确定和非线性的离散的随机系统，设计了一种鲁棒滑模控制器。文献[4]针对巡航导弹的俯仰通道干扰较多的问题，提出了一种二阶滑模变结构算法，仿真表明该算法鲁棒性好。文献[5]针对欠驱动的非线性动态系统的轨道跟踪，设计了一种自适应模糊分层的滑模控制器，快速的跟踪指令。

本文针对超音速靶弹的带有不确定项的姿态运动模型，将快速二阶滑模控制和反演设计相结合，给出了一种适用于超音速靶弹的快速二阶滑模反演控制方法。在两步的反演设计过程中均采用快速二阶滑模控制补偿非匹配和匹配不确定性，将跟踪误差限制在有效范围内。

1靶弹姿态动力学模型

为方便研究问题，假设靶弹动力学模型有以下几个特点：质量、速度、转动惯量变化缓慢，在弹道特征点上可将其视为常数；靶弹弹体是轴对称的且将其视为刚体；靶弹飞行过程中的攻角和侧滑角均看作小量；忽略舵机的滞后。基于以上假设，简化推导出靶弹的带有外界干扰和建模不确定性的姿态运动模型如下

(1)

其中各动力学系数表达式

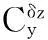
Δai(i=1、2、3、4、6)，Δbi(i=1、2、3、4、6)均为参数摄动值。

将靶弹的姿态动力学模型变形为具有不确定性的标准块控型模型，如下

(2)

(3)

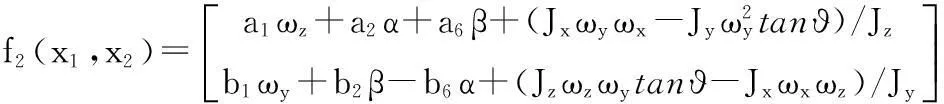
2快速二阶滑模控制器设计

靶弹的标准块控姿态模型中存在着姿态角方程非匹配不确定项和角速度方程匹配不确定项，且不确定项界限难以准确获得。为了消除不确定项的影响并快速的跟踪指令，设计控制器时利用高阶滑模干扰观测器来对不确定项进行估计，然后结合一种快速二阶滑模控制方法来设计控制系统。

2.1设计虚拟控制量x 2d

首先选择姿态角回路滑模面σ1为

(4)

其中， e1=x1-x1d，x1d为期望姿态角的轨迹，且c1>0是常数。

由式(2)、式(4)可得

g1x2+F1

(5)

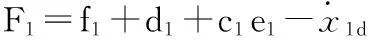
传统的滑模控制方法存在抖振，它不仅影响控制精度，而且容易激发系统中的高频未建模特性，使系统性能变差。本文采用姿态快速二阶滑模控制，得到虚拟控制量如下

(6)

式(6)中，m>2,a1,a2,a3,a4>0为常数。

将虚拟控制量式(6)代入式(5)，得到闭环系统的滑模动态为

(7)

从式(7)中可以看出，当位置距离σ1=0较远时，线性项的系数a2、a4决定了收敛速度，当位置接近σ1=0时，非线性项的系数a1、a3决定了收敛速度，因此无论系统的状态是否远离平衡点都可以通过调节系数获得较快的收敛速度。

令pi=σ1i,i=1,2，将式(7)改写为二阶非线性系统如下

(8)

选择如下Lyapunov函数

V1i=ξTQξ

(9)

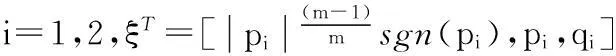
则V1i连续正定，且径向无界。

对V1i求导并将式(8)代入得：

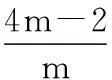
(10)

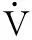
(11)

式(11)中

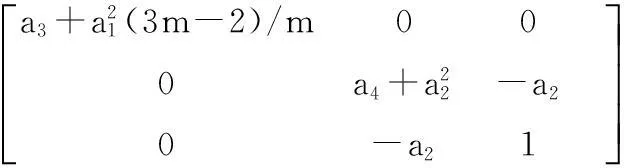
当参数满足如下条件时

(12)

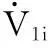
(13)

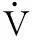
在存在非匹配的不确定性d1的情况下，通过虚拟控制量x2d的作用，且参数满足式(12)，子系统式(2)的跟踪误差e1i到达滑模面σ1i，据式(4)，e1i将渐近收敛到零，即姿态角x1渐近跟踪上指令信号x1d。

2.2设计实际控制量u

角速度回路滑模面σ1为

(14)

其中，虚拟跟踪误差e2=x2-x2d，且c2>0是常数。

由式(3)和式(14)可得

g2u+F2

(15)

本文的控制对象飞行速度快，要求控制系统快速的跟踪上指令信号，故对控制方法的快速性要求高。传统的滑模控制方法响应速度快，但存在抖振，它不仅影响控制精度，而且容易激发系统中的高频未建模特性，使系统性能变差。故本文采用响应速度快且控制量无抖振的快速二阶滑模控制

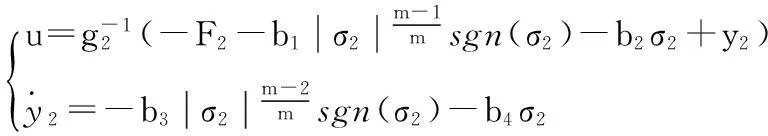
(16)

式(16)中，b1,b2,b3,b4>0为常数。

将控制量u代入式(15)，得到闭环系统的滑模动态为

(17)

令wi=σ2i,i=1,2，将式(16)改写为二阶非线性系统如下

(18)

选择如下Lyapunov函数

V2i=ζTPζ

(19)

则V2i连续正定，且径向无界。

对V2i求导并将式(18)代入得

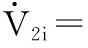
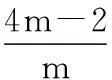
(20)

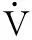
(21)

式(21)中

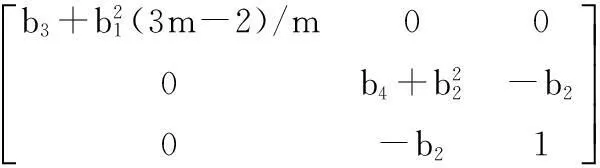
当参数满足如下条件时

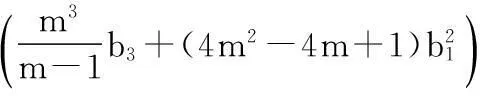
(22)

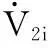
(23)

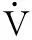
2.3设计滑模干扰观测器

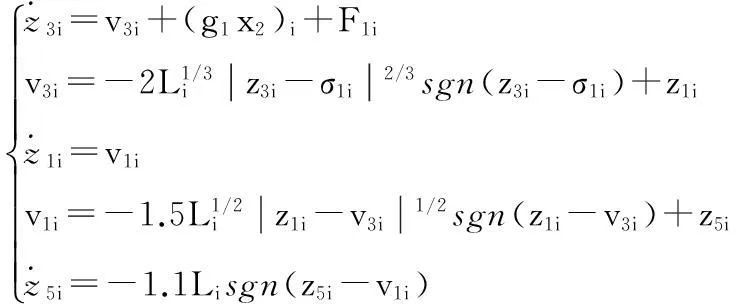
(24)

(25)

其中i=1,2，Li为Lipschitz常数，σ,x2,u实时可得。故采用上述观测器可以精确地得到不确定项的任意阶导数。

3仿真研究

为验证设计方法的可行性，主要针对某旋转靶弹跟踪攻角和侧滑角的情况进行仿真，仿真的初始状态参数如表1所示。选取某特征点飞行速度为V0=800 m/s，高度为h=100m，滚转角速度恒为ωx=10r/s。仿真过程中使各动力学参数摄动±30%，设计的控制器参数：m=3, c1=0.1，a1=0.2，a2=0.1，a3=0.4，a4=0.3，c2=0.1，b1=0.6，b2=0.2，b3=b4=0.3。

表1　仿真初始状态参数

图1为本文的快速二阶滑模反演控制与常规滑模控制对比跟踪正弦攻角指令的响应曲线，图2为本文研究的控制与常规滑模跟踪阶跃侧滑角指令的响应曲线，图3为两种控制方法跟踪攻角指令时产生的俯仰等效舵偏角曲线，图4为两种控制方法跟踪侧滑角指令时产生的偏航等效舵偏角曲线。

从图1、图2可以看出由于不确定性和干扰的存在，初始阶段出现较大跟踪误差，稳定后也存在小幅度的振荡，但对控制效果影响不大。将快速二阶滑模反演控制与常规滑模控制相比：其能够更快的跟踪上指令信号，有利于超音速靶弹快速姿态控制；跟踪过程中其能够更靠近指令信号，跟踪效果更好。从图3、图4可以看出快速二阶滑模反演控制与常规滑模控制相比，跟踪指令时其产生的等效舵偏角基本没有高频抖振现象，有利于舵机系统执行指令。

图1　攻角响应曲线

图2　侧滑角响应曲线

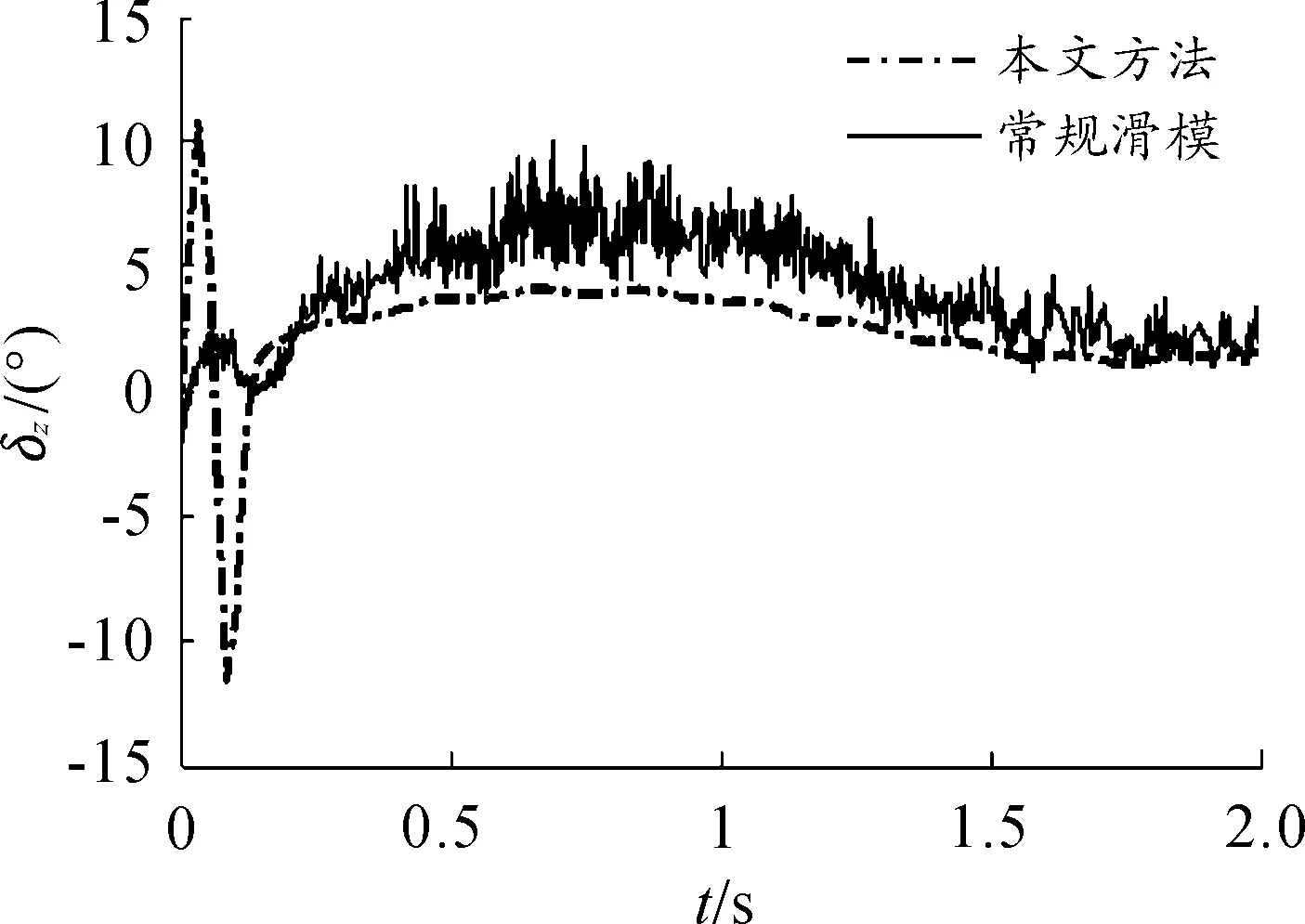
图3　俯仰等效舵偏角变化曲线

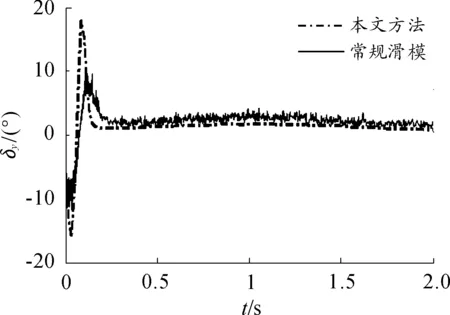
图4　偏航等效舵偏角变化曲线

4结论

本文针对带有外界干扰和建模不确定性的靶弹姿态运动模型，将快速二阶滑模控制和反演控制相结合，设计了一种新的超音速靶弹反演滑模控制器。该控制器能够快速响应姿态角指令，适用于超音速飞行靶弹的姿态控制，该控制器也具有良好的鲁棒性，能够处理外界干扰和建模不确定性带来的影响。设计中采用线性项和非线性项使滑模变量快速收敛到原点，使得响应速度提升。且设计的不连续控制量作用在滑模变量的高阶导数上，解决了传统滑模控制的高频抖振问题，使其具有一定的工程应用价值。

参考文献：

[1]朱凯，齐乃明，秦昌茂.基于二阶滑模的BTT导弹反演滑模控制[J].系统工程与电子技术，2010，32(4)：829-832.

[2]TakeshiYamasaki，BalakrishnanSN，HiroyukiTakanoetc.SecondOrderSlidingMode-BasedInterceptGuidancewithUncertaintyandDisturbanceCompensation[C]//AIAAGuidance,Navigation,andControl(GNC)Conference，2013.

[3]李亚平.基于无向连通图理论的矩阵集结方案的优化[J].重庆工商大学学报：自然科学版，2014，31(5)：10-13.

[4]JunHu，ZidongWang，HuijunGaoetc.RobustSlidingModeControlforDiscreteStochasticSystemsWithMixedTimeDelays,RandomlyOccurringUncertainties,andRandomlyOccurringNonlinearities[J].IEEETransactionsonIndustrialElectronics，2012，59(7)：3008-3015.

[5]于进勇，顾文锦，赵红超.飞航导弹纵向控制系统的二阶滑模控制系统设计[J].系统仿真学报，2003，15(9)：1319-1321.

[6]曹小平，程静.基于微信的自助查询系统的设计与实现[J].重庆工商大学学报：自然科学版，2014，31(2)：66-69.

[7]Chih-LyangHwang，Chiang-ChengChiang，Yao-WeiYeh.AdaptiveFuzzyHierarchicalSliding-ModeControlfortheTrajectoryTrackingofUncertainUnderactuatedNonlinearDynamicSystems[J].IEEETransactionsonFuzzySystems，2014，22(2)：286-299.

(责任编辑周江川)