3电机同步系统的2阶模糊免疫自抗扰控制

李 慧，刘星桥，李 景

3电机同步系统的2阶模糊免疫自抗扰控制

李 慧1，2，刘星桥1，李 景2

（1.江苏大学电气信息工程学院，江苏镇江212013；2.淮阴工学院电子与电气工程学院，江苏淮安223001）

为了解决系统快速响应和小超调之间的矛盾，进一步提高控制系统的控制性能，结合免疫控制理论和自抗扰控制（ADRC）技术提出了2阶模糊免疫自抗扰控制策略.利用生物自适应免疫机制来提高控制系统的鲁棒性能，在一定程度上解决了小超调和系统上升时间短之间的矛盾；利用2阶自抗扰技术实现了速度和张力的强解耦；利用模糊算法实现了非线性智能免疫控制；同时对控制系统的稳定性进行了证明.仿真和试验结果表明，该控制策略要明显优于传统的PID控制，采用该控制策略的系统响应速度快，超调量小，解耦能力强，跟踪精度高，抗干扰能力强.

免疫；自抗扰；响应速度；解耦；跟踪精度

多电机同步协调控制在现代工业生产中应用广泛，尤其在造纸、轧钢、纺织等行业的拉伸及卷绕环节.3变频器驱动3台电机构成了多输入多输出、非线性、强耦合的复杂3电机同步系统.3电机能够协调同步运转就要求能够实现速度和张力的解耦.对于传统的proportion integral derivative（PID）控制，还存在一定的技术瓶颈［1］.针对电机协调控制的相关课题，国内外学者进行了广泛深入的研究［2-5］.

免疫控制是基于生物自然免疫原理发展而来的一种反馈控制技术，广泛应用于工业控制领域［6-9］.文献［6］将免疫记忆、克隆选择以及亲和力计算应用于解决协调问题的处理上，降低了系统的复杂程度，实现了多任务代理协调机制，取得了一定的效果；文献［7］提出基于模糊规则的无刷直流电机免疫PID控制，利用模糊控制器实现免疫PID控制，通过对无刷电机转速的仿真和试验，对传统PID控制的一些不足加以改进，具有一定的抗干扰性能.

中国科学院韩京清研究员从PID控制原理出发提出了自抗扰控制技术.自抗扰控制吸取了现代控制理论成果，在一定程度上提高了控制系统的控制品质和控制精度，尤其适合于恶劣环境下的要求高速高精度控制场合［10-13］.在多电机协调同步控制领域，自抗扰控制技术应用广泛［14-16］.文献［14］提出了一阶自抗扰控制策略，将优化后的一阶自抗扰技术应用到3电机协调同步控制中.文献［15］在文献［14］的基础上提出了2阶自抗扰控制技术，也取得较好的控制效果.文献［16］将模糊控制算法与自抗扰控制相结合控制3电机同步运转，提出了模糊自抗扰控制策略，通过简单的模糊推理对自抗扰参数进行在线整定.

文中基于前人的工作，结合免疫控制理念和自抗扰控制技术，提出2阶免疫自抗扰控制策略.将生物免疫原理作为自抗扰参数整定的基础，采用模糊算法实现免疫机理；利用免疫控制的生物机能自适应调节特性以及反馈原理，解决控制系统的超调量和响应快速性之间的矛盾.

1 3电机同步控制系统数学模型

3电机同步系统结构图如图1所示，由控制器控制3台变频器分别驱动3台交流异步电动机，构成3电机同步系统，实现电机速度和张力的协调运行.

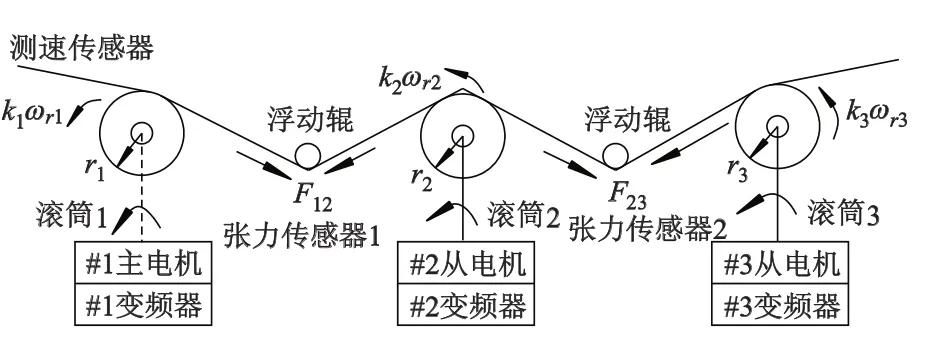
图1 3电机系统模型

根据文献［14］，当3台变频器都工作在矢量控制模式下，3电机同步系统的数学模型可以被表达为

式中：x=［ωr1ωr2ωr3F12F23］T为系统的状态变量；u=［ω1ω2ω3］T为外输入信号.在变频器矢量控制方式下，假设转子磁链不变化，系统方程可以简化［17］为

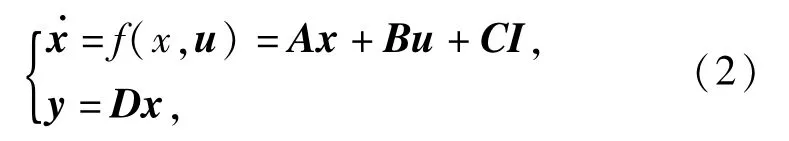
其中

式中：F12，F23为电机两两之间的皮带张力，kg；ω1，ω2，ω3为

外输入给定的电机同步旋转角速度，rad·min-1；ωr1，ωr2，ωr3为3台电机的转子电气角速度；r1，r2，r3为第1，2，3台电机胶带滚筒的半径，m；i1，i2，i3为3台电机的速比；K1，K2为传递系数；T1，T2为张力变化常数；Ψr1，Ψr2，Ψr3为3台电机的转子磁链，Wb；J1，J2，J3为3台电机转动惯量，kg·m2；TL1，TL2，TL3为3台电机的负载转矩，N·m；Tr1，Tr2，Tr3为3台电机的时间常数，s；Lr1，Lr2，Lr3为3台电机的转子电感，H；np1，np2，np3为3台电机的极对数.

2 控制策略设计

总控制系统主要包括3路2阶免疫自抗扰控制器与3电机同步系统（控制对象），总体结构如图2所示.

图2 中，ωref为主电机速度控制器的参考信号，F12-ref为张力1控制器的参考信号，F23-ref为张力2控制器的参考信号.

2.1 2阶自抗扰控制设计

文中控制方式采用主从控制方式，根据式（1），系统的状态方程可以表示为

式中：f0（x（0），x（1），…，x（n-1），t）+b0u为系统的已知部分；f1（x（0），x（1），…，x（n-1），w（t））+b1u为系统的未知部分，可以采用2阶自抗扰控制来实现.active disturbance rejection control（ARDC）主要由tracking differentiator（TD）、extended state observer（ESO）、nonlinear state error feedback（NLSEF）、扰动补偿几部分构成［10］.为了降低系统非线性计算的复杂性，提高系统的实时性能，文中采用2阶免疫自抗扰控制方式，忽略TD的影响，用模糊非线性免疫增益控制置换NLSEF环节，保留扩张状态观测器ESO，对系统的内外综合扰动进行补偿.

在2阶自抗扰控制中，ESO有至关重要的作用，它根据系统的输入和反馈输出，将影响系统输出的总体扰动作用扩张成为一个新的状态变量，进行统一观测和补偿.由于ESO只用到被控系统的输入和输出信息，没有用到描述被控对象的函数的任何信息，因此，不要求清晰地了解被控制对象的结构.对应2阶自抗扰控制，采用3阶的ESO，对ESO控制算法采用欧拉法进行离散化，之后得到的具体设计算法如式（4）所示.

式中：i为子控制系统编号（1：主电机速度控制模块，2：张力1控制模块，3：张力2控制模块）；ei1为第i子控制系统的跟踪误差；zi1为第i子控制系统输出yi的跟踪信号；zi2为yi的微分输出信号；zi3为第i子控制系统的未知扰动总和的观测值；h为离散系统的采样时间；ui0为第i子控制系统的免疫控制器输出信号；ui为第i子控制系统的总控制器输出信号；bi0为自抗扰控制的补偿因子；βi1，βi2，βi3为第i子控制系统输出误差的校正增益；fal为幂次函数；δ为线性空间.

2.2 模糊免疫控制器设计

2.2.1 免疫控制器设计

现代免疫控制的实质是基于生物免疫抵抗原理的非线性增益控制，可以将目标函数作为抗原，问题的求解作为抗体.

生物免疫系统可以通过在体内产生某种抗体来抵御外来侵犯的抗原.生物的免疫系统由淋巴细胞（T细胞和B细胞）和抗体分子组成，其中淋巴T细胞又分为TH（辅助细胞）和TS（抑制细胞），当抗原侵入机体，将会刺激B细胞，B细胞将会产生一定的抗体来消除抗原.B细胞产生抗体的多少与淋巴细胞（TH和TS）有关.当抗原较多的时候，产生的TH细胞多，TS细胞则较少，从而会产生较多的B细胞；反之，如果TH细胞少，TS细胞较多，从而产生较少的B细胞，经过一段时间后，生物体内达到平衡.

免疫控制正是通过免疫系统能够自动抵御抗原的自适应参数调节特性来实现系统控制的，使得控制系统具有很强的鲁棒性能.

将第i子控制系统的系统误差ei看作抗原，控制输入ui0作为B细胞接收的总刺激S.则有：

式中：li1为促进系数，li2为抑制系数，都是正数；ui为第i子控制系统的控制量输出；Δui为ui的变化率；ei是第i子控制系统的系统误差；f（ui，Δui）为一选定的非线性函数.为简化表示，将f（ui，Δui）记为fi，则B细胞接收的总刺激为

因此

式中：Kpi=li1为免疫控制器的增益，决定系统响应速度；ηi=li2/li1在一定程度上决定系统稳定的效果.

结合2阶自抗扰控制算法，得到2阶免疫自抗扰具体的结构图如图3所示.图中zi2是输出信号的微分项，而系统采用非线性比例控制方式，没有用到微分项，因此图中没有标出.

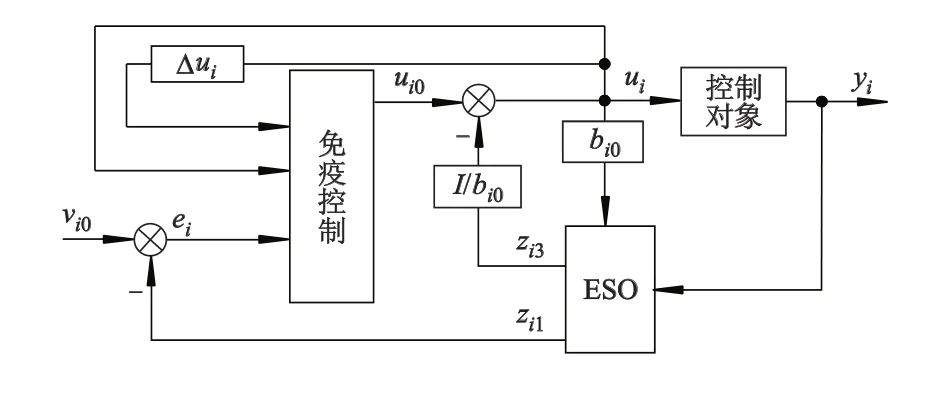
图3 2阶免疫自抗扰控制结构图

2.2.2 免疫控制器实现

免疫控制器实质上是一种非线性的增益控制，为了提高系统的快速响应性能，采用基于查表的模糊控制算法逼近非线性增益函数fi.

将子控制系统的输出ui以及输出的变化率Δui作为模糊控制器的输入，非线性增益函数fi作为模糊控制器的输出.对每个输入变量进行二模糊集模糊化，分别为“正”（P）和“负”（N），输出变量进行3模糊集模糊化，分别是“正”（P）、“零”（Z）和“负”（N）.模糊控制器采用以下4条规则：

在以上规则中，使用Zadeh的模糊逻辑AND操作，采用常用的mom反模糊化方法得到模糊控制器的输出fi.

结合自抗扰控制算法（见式（4））和免疫控制方程（见式（8））进行推导，可以得到控制器的总体方程（9）.

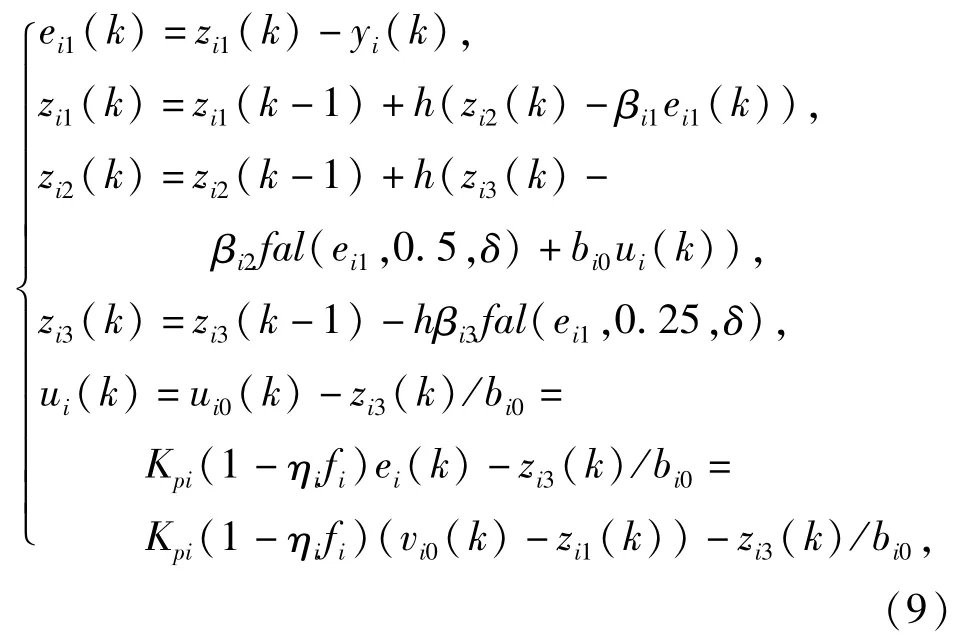
式中vi0为第i子控制系统的输入参考信号（i=1，2，3）.v10=ωref，v20=F12-ref，v30=F23-ref.

3 控制器参数整定

控制参数主要包括免疫控制器参数Kpi和ηi，以及ESO中的βi1，βi2，βi3（i=1，2，3），采样间隔h选100 ms.文献［10］中ESO的数值仿真研究表明，参数βi1，βi2，βi3由系统的采样步长决定，其中βi1=1/ h，βi2=1/（3×h2），βi3=2/（64×h3）.取h=0.1 s，因此βi1，βi2，βi3分别选取为10.0，32.5，33.0.免疫控制参数Kpi直接影响着系统响应的速度，间接影响到系统的稳态误差，ηi是反应系统稳定性的参数，适当的调大ηi可以抑制系统的超调量，通过合理的调整Kpi参数和ηi参数可以在一定程度内解决响应速度和系统超调之间的矛盾.本着这个原则，多次仿真调试之后得到控制器的仿真控制参数如下：主电机模块参数为Kp1=1.701，η1=0.6，β11=10.0，β12=32.5，β13=33.0，b10=1.0；张力1控制模块参数为Kp2=10.204，η2=0.6，β21=10.0，β22=32.5，β23=33.0，b20=1.0；张力2控制模块参数为Kp3= 5.102，η3=0.8，β31=10.0，β32=32.5，β33=33.0，b30=0.4.

4 稳定性证明

首先根据3电机同步系统方程（见式（1））结合免疫自抗扰控制方程（见式（9）），经过推导，控制信号可以表述为

由文献［10］可知，zi1紧紧跟随ωri，为了讨论控制系统稳定性的方便，可以假设zi1=ωri，zi3是ESO的扰动总和的观测值，在剔除了已知部分信号之后，zi3可以看成负载扰动，代入控制信号表达式得出：

式中fi（i=1，2，3）为免疫控制的3路非线性函数，由模糊算法实现，且有：fi是一组非线性函数，代入系统方程后，系统变成了非线性控制系统，但是fi范围在［-1.0，1.0］.要分析整个非线性系统的稳定性，首先可以将该非线性系统分割成若干个时段的线性系统，对应每个时段的线性系统都有-1.0≤fi≤1.0.

电机控制参数为

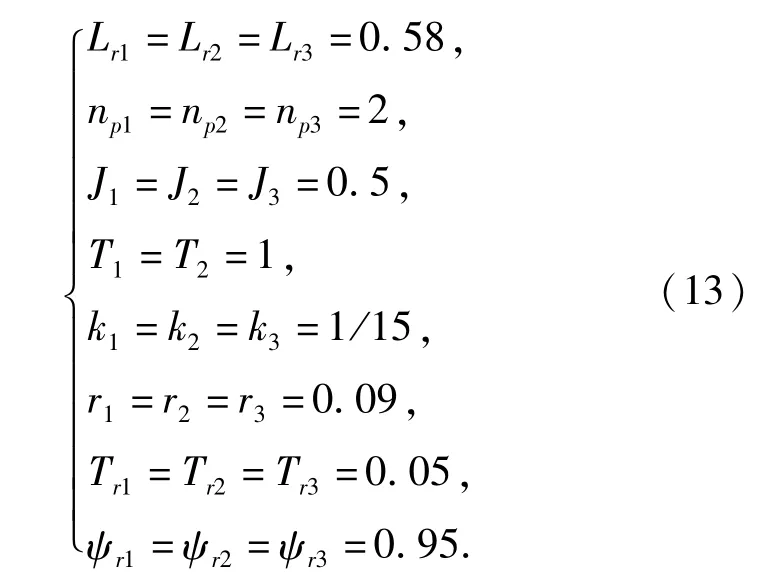
将以上参数代入第1节中的系统数学模型式（2），得到如下标准形式：

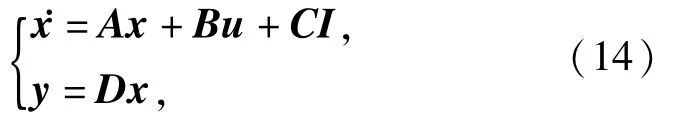
其中，系统矩阵A可求，得到

A的全部特征值为-0.992 7，-0.977 2，-0.645 2，-0.622 4，-0.629 7，全部为负数，可知，原系统矩阵A为负定矩阵.

将控制信号表达式（10）代入原系统，置换原系统中的输入信号ωi，经过整理后得到控制系统的新的系统矩阵A′，即为

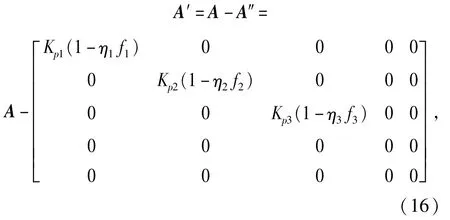
显然，对应若干时段的子线性系统，只要Kpi（1-ηifi）＞0，A″即为正定对角阵，即A′为负定矩阵，则对应的所有子线性控制系统的全部特征值均小于0，即所有的子线性控制系统都稳定，则总非线性控制系统稳定.由-1.0≤fi≤1.0，Kpi＞0，ηi＞0，因此，只要0＜ηi＜1，A″的所有无素均为正数，故A″为正定对角阵，而A为负定矩阵，因此A′为负定矩阵，系统稳定.而由系统参数选择知：η1=η2= 0.6，η3=0.8，显然符合条件，因此，整个控制系统稳定.

5 仿真和试验研究

5.1 仿真研究

在Simulink环境下对3电机同步控制系统进行建模仿真，代入电机参数（见式（13）），用S函数对3电机系统进行建模，分别应用PID控制和2阶免疫自抗扰控制策略，对控制系统主电机速度的抗干扰性能、方波跟踪性能等方面进行仿真测试.

5.1.1 抗干扰测试

给定幅度为300 rad·min-1的阶跃信号，仿真20 s时间，在16 s处，在控制输入端对控制对象叠加脉宽为1 s幅度为300的三角波干扰信号，分别应用传统PID控制策略和2阶免疫自抗扰控制策略进行测试，仿真响应曲线如图4所示.

图4 抗干扰测试仿真曲线

从图4可见，采用传统PID控制策略的控制系统上升时间较长，动态响应迟缓，而采用2阶免疫自抗扰控制的系统响应速度快，调节时间短，基本没有超调量.对应出现的三角波干扰信号，采用传统PID控制策略的系统响应最大突变为13.75 rad· min-1，为系统稳态输出的4.58%，采用2阶模糊免疫自抗扰控制策略的系统最大响应突变为6.05 rad·min-1，为系统稳态输出的2.02%，可见采用模糊免疫自抗扰控制策略的系统的抗干扰特性要远远好于传统PID控制策略.

5.1.2 方波跟踪测试

给定主电机速度为幅度300 rad·min-1，周期为8 s的占空比1∶1的对称方波，分别应用传统PID控制策略和2阶免疫自抗扰控制策略进行测试，系统仿真响应曲线如图5所示.

从图5可见，采用传统PID控制策略的系统响应速度慢，跟踪方波存在较大的稳态跟踪误差，最小稳态跟踪误差为0.71 rad·min-1，为系统稳态输出的0.237%，而采用2阶免疫自抗扰控制策略的系统响应速度快，最小稳态跟踪误差为0.005 4 rad· min-1，为系统稳态输出的0.001 8%，跟踪效果要明显优于传统的PID控制策略.

图5 方波跟踪仿真曲线

5.2 试验验证

为进一步验证控制策略的可行性，采用同样的电机参数，用DSP2812以及CPLD搭建3电机同步控制系统，进行试验验证.由CPLD组建RS485总线控制3个变频器驱动3个电机工作，用一个圆光栅编码器测量主电机速度，用2个SL-100张力传感器来检测张力.分别采用传统PID以及免疫自抗扰2种控制策略对系统的解耦性能，跟踪性能等方面进行了试验，3台交流异步电机的额定转速为1 470 rad·min-1，额定频率50 Hz，采用变频器矢量控制方式.控制信号转换成为频率信号后传送给变频器，比例为1 470/50=29.4，具体试验平台如图6所示.

对试验装置参数进行反复试验调整，最终确定了试验系统的控制参数，即免疫自抗扰控制下的各模块的控制参数如下：主电机模块参数为Kp1= 1.734 2，η1=0.6，β11=10，β12=32.5，β13=33，b10= 1；张力1控制模块参数为Kp2=8，η2=0.6，β21=10，β22=32.5，β23=33，b20=1；张力2控制模块参数为Kp3=5.102，η3=0.8，β31=10，β32=32.5，β33=33， b30=0.4.PID控制方式下的各模块控制参数如下：主电机模块PID控制参数为Kp1=0.11，Ki1=0.04，Kd1=0.001；张力1控制模块参数为Kp2=30，Ki2= 0.1，Kd2=0.001；张力2控制模块参数为Kp3=30，Ki3=0.1，Kd3=0.001.

图6 试验平台照片

5.2.1 控制系统解耦性能测试

速度和张力的解耦是3电机同步协调控制的保证，在速度恒定、张力发生变化时要求速度能够不受影响，实现速度和张力的解耦.主电机参考速度ωref恒定设定在300 rad·min-1，对电机张力参考给定F12-ref和F23-ref在80 s处突降，F12-ref从15 kg突降到11 kg，张力F23-ref从12 kg突降到8 kg，对PID控制和2阶免疫自抗扰控制分别进行了试验，对试验曲线在70～90 s进行放大，结果如图7所示.

图7 速度恒定张力突降响应

从图7可见，当速度恒定、张力突降时，对应PID控制，电机速度受到一定的影响，而对应2阶免疫自抗扰控制，电机速度基本不受影响，具体动态性能及解耦效果见表1.

表1 张力突降下的电机解耦性能指标

由此可见，2阶免疫自抗扰控制的解耦性能明显要优越于传统的PID控制；另外，从动态性能方面，张力在突降后2阶免疫自抗扰控制的系统能够迅速得到稳定，而传统的PID控制效果要差很多，即2阶免疫自抗扰响应速度更快，超调量小，具有良好的动态性能.

5.2.2 方波跟踪性能测试

给定主电机速度控制器的参考速度ωref为幅值350～250 rad·min-1的方波信号，采用PID控制和2阶免疫自抗扰控制2种控制方式分别进行了跟踪试验，试验结果如图8所示.

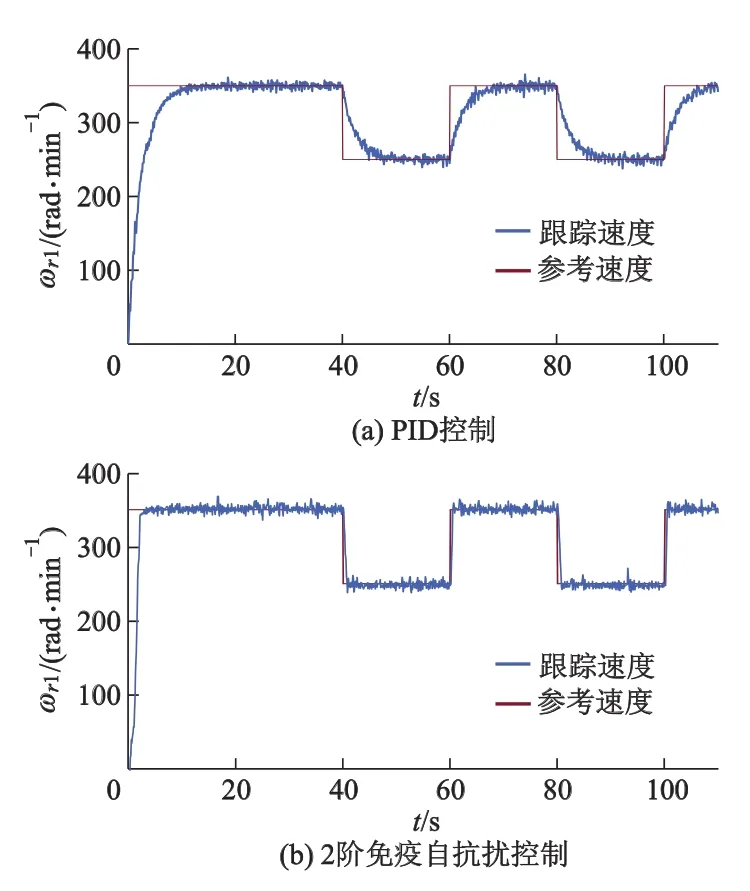
图8 方波跟踪性能测试

从图8可见，采用传统的PID控制，在输入信号发生突变时，要10 s左右的过渡时间才能跟踪上参考信号，跟踪迟缓，跟踪误差比较大；而采用2阶免疫自抗扰控制的系统跟踪迅速，在参考信号发生突变时，在初始启动时2 s以内能跟踪参考信号，在系统启动后0.6 s左右就能够跟随输入的参考信号，动态性能好，跟踪误差小.同时在超调量方面，经过合理的调整免疫参数可以将2阶免疫自抗扰的超调量控制在允许范围之内.

6 结 论

1）利用免疫系统的记忆能力和反馈原理，在一定程度上可以解决降低系统超调量和提高系统快速响应性能之间的矛盾.

2）利用2阶自抗扰控制器的强解耦能力实现速度和张力等参数的解耦控制.

3）在既定参数下证明了本控制系统的稳定性.

4）2阶模糊免疫自抗扰控制策略在系统动态性能、跟踪精度以及抗干扰性能等方面都明显要优越于传统的PID控制，为3电机同步协调系统提供了一种新的可行的解决方案.

（

）

［1］ Anderson R G，Meyer A J，Valenzuela M A，et al.Web machine coordinated motion control via electronic lineshafting［J］.IEEE Transactions on Industry Applications，2001，37（1）：247-254.

［2］ 刘 然，孙建忠，罗亚琴，等.基于环形耦合策略的多电机同步控制研究［J］.控制与决策，2011，26（6）：957-960. Liu Ran，Sun Jianzhong，Luo Yaqin，et al.Research on multi-drive synchronization control based on ring coupling strategy［J］.Control and Decision，2011，26（6）：957-960.（in Chinese）

［3］ Wang Gaolin，Li Tielian，Zhang Guoqiang，et al.Position estimation error reduction using recursive-least-square adaptive filter for model-based sensorless interior permanent-magnet synchronous motor drives［J］.IEEE Transactions on Industrial Electronics，2014，61（9）：5115-5125.

［4］ 刘国海，杨官学，沈 跃，等.基于神经网络广义逆的两电机变频系统内模控制［J］.电工技术学报，2010，25（11）：56-61，67. Liu Guohai，Yang Guanxue，Shen Yue，et al.Internal model control of two motor variable frequency systems based on network generalized inverse［J］.Transactions of China Electrotechnical Society，2010，25（11）：56-61，67.（in Chinese）

［5］ Liu Guohai，Liu Pingyuan，Shen Yue，et al.Experimental research on decoupling control of multi-motor variable frequency system based on neural network generalized inverse［C］∥Proceedings of 2008 IEEE International Conference on Networking，Sensing and Control.Sanya，China：IEEE Computer Society，2008：1476-1479.

［6］ 梁志伟，郑重虎，沈 杰，等.基于人工免疫系统的多智能体任务分配策略［C］∥第25届中国控制与决策会议论文集.贵阳：IEEE，2013：3486-3491.

［7］ 夏长亮，刘 丹，王迎发，等.基于模糊规则的无刷直流电机免疫PID控制［J］.电工技术学报，2007，22（9）：68-73. Xia Changliang，Liu Dan，Wang Yingfa，et al.Control of brushless DC motors using fuzzy set based immune feedback PID controller［J］.Transactions of China Electrotechnical Society，2007，22（9）：68-73.（in Chinese）

［8］ 詹永照，汪满容，柯 佳.基于人工免疫有序聚类的视频关键帧提取方法［J］.江苏大学学报：自然科学版，2012，33（2）：199-204. Zhan Yongzhao，Wang Manrong，Ke Jia.Video keyframe extraction using ordered samples clustering based on artificial immune［J］.Journal of Jiangsu University：Natural Science Edition，2012，33（2）：199-204.（in Chinese）

［9］ 杨建宁，孙玉坤，成 立，等.采用免疫搜索的电网电压非线性模型预测控制［J］.江苏大学学报：自然科学版，2008，29（1）：56-60. Yang Jianning，Sun Yukun，Cheng Li，et al.Nonlinear model predictive scroll control with artificial immune algorithm for voltage security［J］.Journal of Jiangsu University：Natural Science Edition，2008，29（1）：56-60.（in Chinese）

［10］ 韩京清.自抗扰控制技术---估计补偿不确定因素的控制技术［M］.北京：国防工业出版社，2008.

［11］ Cai Tao，Zhang Han，Gu Lei，et al.On active disturbance rejection control of the payload position for gantry cranes［C］∥Proceedings of the 2013 American Control Conference.Washington：IEEE，2013：425-430.

［12］ Liu Ruijuan，Wu Min，Liu Guoping，et al.Active disturbance rejection control based on an improved equivalent-input-disturbance approach［J］.IEEE/ASME Transactions on Mechatronics，2013，18（4）：1410-1413.

［13］ Zhao Shen，Gao Zhiqiang.An active disturbance rejection based approach to vibration suppression in two-inertia systems［C］∥Proceedings of the2010 American Control Conference.Baltimore，MD，United States：IEEE Computer Society，2010：1520-1525.

［14］ 刘星桥，胡建群，周 丽.自抗扰控制器在三电机同步系统中的应用［J］.中国电机工程学报，2010，30（12）：80-85. Liu Xingqiao，Hu Jianqun，Zhou Li.Active disturbance rejection control of three-motor synchronous control system［J］.Proceedings of the CSEE，2010，30（12）：80-85.（in Chinese）

［15］ 刘星桥，唐 琳，周 丽.二阶自抗扰控制器在三电机同步系统中的应用［J］.电工技术学报，2012，27（2）：179-184. Liu Xingqiao，Tang Lin，Zhou Li.Second-order active disturbance rejection controller applied in three-motorsynchronous system［J］.Transactions of China Electrotechnical Society，2012，27（2）：179-184.（in Chinese）

［16］ 刘星桥，唐 琳，朱丽婷.模糊自抗扰控制的三电机同步协调系统［J］.电机与控制学报，2013，17（4）：104-109. Liu Xingqiao，Tang Lin，Zhu Liting.Three-motor synchronous control system based on fuzzyactive disturbances rejection control［J］.Electric Machines and Control，2013，17（4）：104-109.（in Chinese）

［17］ Zhang Hao，Yu Kun，Liu Guohai，et al.Fuzzy self-tuning decoupling control based on neural network of three-motor drive system［J］.Control Theory&Applications，2013，30（9）：1178-1186.

（责任编辑 梁家峰）

Second-order fuzzy immune active disturbance rejection control scheme of three-motor synchronous system

Li Hui1，2，Liu Xingqiao1，Li Jing2
（1.School of Electrical and Information Engineering，Jiangsu University，Zhenjiang，Jiangsu 212013，China；2.Faculty of Electronic and Electrical Engineering，Huaiyin Institute of Technology，Huainan，Jiansu 223001，China）

In order to solve the contradiction between system fast response and small overshoot，and to further improve the control performance of control system，the second-order fuzzy immune active disturbance rejection control（ADRC）strategy was proposed combined with immune control theory and ADRC technology.The robustness of the control system was improved by bio-adaptive immune mechanisms，and the contradiction between small overshoot and short rise time was resolved to some extent.Speed and tension were strongly decoupled by the second-order ADRC technology.Nonlinear intelligent immune control was achieved by fuzzy algorithm.The stability of control system was proved.The results of simulations and experiments show that the control strategy is superior to the traditional PID control.The two-order fuzzy immune ADRC has rapid response speed，strong decoupling ability，high tracking accuracy and strong anti-interference ability.

immune；ADRC；response speed；decouple；tracking accuracy

TP273

A

1671-7775（2015）02-0201-08

李 慧，刘星桥，李 景.3电机同步系统的2阶模糊免疫自抗扰控制［J］.江苏大学学报：自然科学版，2015，36（2）：201-208.

10.3969/j.issn.1671-7775.2015.02.014

2014-07-25

国家自然科学基金资助项目（60874014，51273154）；江苏高校优势学科建设工程资助项目（PAPD，NO.6-2011）；江苏省2013年度普通高校研究生科研创新计划项目（CXLX13-669）；江苏省科技支撑计划项目（BE2013402）

李 慧（1980-），男，江苏淮安人，博士研究生（13645234923@163.com），主要从事多电机同步复杂控制研究.刘星桥（1960-），男，江苏镇江人，教授，博士生导师（xqliu@ujs.edu.cn），主要从事多电机和其他复杂系统控制理论及应用研究.