自由活塞斯特林发动机配气活塞阻尼系数的试验研究

李 薇 牟 健 洪国同

(1中国科学院理化技术研究所 北京 100190)

(2中国科学院大学 北京 100049)

1 引言

自由活塞斯特林发动机是斯特林发动机的一个重要分支，它取消了曲柄连杆机构，采用间隙密封、柔性支撑等技术［1-2］。在空间电源、热电联产、船舶潜艇等领域有着越来越广泛的应用［3-5］。在自由活塞斯特林发动机动力学的设计、分析中，数学模型的建立只是提供了一种可供分析计算的基础，要使分析计算的结果可靠，必须先确定数学模型内的各系数，确定这些参数的过程本身就是一项极有意义并颇有难度的课题［6］。

自由活塞斯特林发动机配气活塞的运动与其运动阻尼密切相关。配气活塞的运动阻尼对冷热腔压力波和配气活塞位移波之间的相位差以及配气活塞位移幅值均有着重要影响，它是一个调整发动机性能的重要参数。配气活塞的运动阻尼主要来自与气体工质的粘性阻尼、配气活塞头与气缸壁的摩擦阻尼、配气活塞杆与动力活塞的摩擦阻尼等，同时，它还受冷、热腔间回热器温度梯度变化的影响。这些因素都决定于整机的运行，配气活塞的运动阻尼是一个运行参数，它的取值因系统而异，变化非常大，至今仍没有一种有效的理论方法加以计算。若想获得准确值，只能在发动机运行过程中通过实验测得［7］。

本文就是在自由活塞斯特林发动机动力学模型的基础上，分析了动力学方程中阻尼项的组成项。根据不同的组成项，设计了不同的阻尼测试实验方案。然后利用自由振动法，得到不同实验方案的自由振动的衰减曲线，计算出阻尼率，进而计算出配气活塞阻尼。

2 数学模型

2.1 振动系统动力学模型

对于单自由度有阻尼的自由振动系统，其运动微分方程为:

或

振动系统固有频率ωn和阻尼率ξ可用下式表示:

所以，若想知道振动系统中的阻尼系数，要先得到该振动系统的阻尼率ξ。

2.2 配气活塞振动系统动力学模型

配气活塞单独动力学实验装置由气缸、配气活塞、动力活塞、加热器、回热器、冷却器、配气活塞驱动电机等组成，具体结构如图1所示。配气活塞上端为热腔，通过高温换热器与热源(加热棒)交换热量。配气活塞下端为冷腔，通过冷却器向外界散热。热腔和冷腔之间通过回热器连接，回热器为环状，位于配气气缸的外侧，与其同轴。冷腔下端是动力活塞，动力活塞固定在实验装置缸体，处于轴向某个位置，保持不动。动力活塞下端是缓冲腔，配气活塞的驱动电机固定在缓冲腔内，通过配气活塞杆(从动力活塞中间穿过)与配气活塞相连。

图1 实验装置结构示意图Fig.1 Schematic diagram of experimental apparatus

自由活塞斯特林发动机的动力学模型可以用机械振动系统来很好的诠释。配气活塞的受力分析如图2所示，其运动方程为:

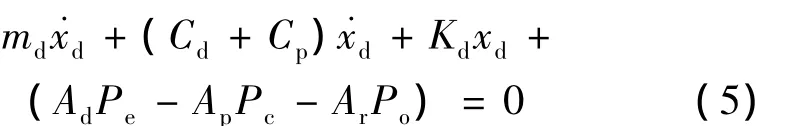
配气活塞的气体力可以等效成气体阻尼力和气体弹簧力(或气体惯性力)的共同作用(另文叙述)，因此，上式可以写成与式(1)相似的形式，即

式中;md为作用在配气活塞的惯性力，kg˙m/s;Cd为配气活塞与气缸体的摩擦阻尼系数，Ns/m;Cp为配气活塞杆与动力活塞内孔的摩擦阻尼系数，Ns/m;Cg为气体工质的粘性阻尼系数，Ns/m;为配气活塞的运动速度，m/s;为配气活塞与气缸之间的运动阻尼，Ns/m;Kd为配气活塞的板弹簧刚度，N/m;Kg为配气活塞的气体弹簧刚度，N/m;xd为配气活塞的运动位移，m;Kdxd为机械弹簧产生的弹簧力，N;Pe为热腔压力，Pa;Pc为冷腔压力，Pa;Pc为缓冲腔压力，Pa;Ad为配气活塞面积，m2;Ar为配气活塞杆面积，m2;Ap为动力活塞面积，m2(其中Ap=Ad=Ar)。

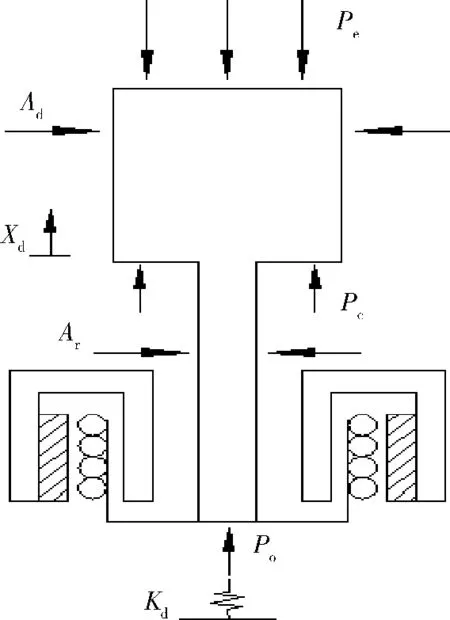
图2 配气活塞的受力示意图Fig.2 Force diagram of displacer

从式(6)可以看出，配气活塞运动的阻尼包括配气活塞头与气缸壁的摩擦阻尼、配气活塞杆与动力活塞内壁的摩擦阻尼和气体工质粘性阻尼。

2.3 阻尼率的测量模型

配气活塞振动系统动力学方程中的参数都可以很容易的测定，主要的困难在于阻尼项中的三个阻尼系数的测定。为了确定配气活塞振动系统中的阻尼率，进而使振动系统的动力学模型更可靠，本实验采用自由振动法。

自由振动法就是采用激振的方法，根据与配气活塞杆相连的位移传感器所记录的活塞自由振动的衰减曲线(图3)，可分析出衰减振动的周期T。在间隔一个振动周期T的任意两时刻t1、t2时，响应的振动位移x(t1)、x(t2)可表示为:

式中:X为振动最大位移幅值，m;ωn为振动系统的固有频率，rad/s，ωd为阻尼自然频率，rad/s。

由于 t2=t1+T=T1+2π/ωd，所以

即

对上式两端取自然对数，则有:

式中，δ为对数衰减率，当由实验测得振动位移x(t1)、x(t2)后，容易算出对数衰减率δ，再根据δ就可以由上式算出阻尼率ξ。

对于间隔个振动周期jT波形，对数衰减率δ可以表示为:

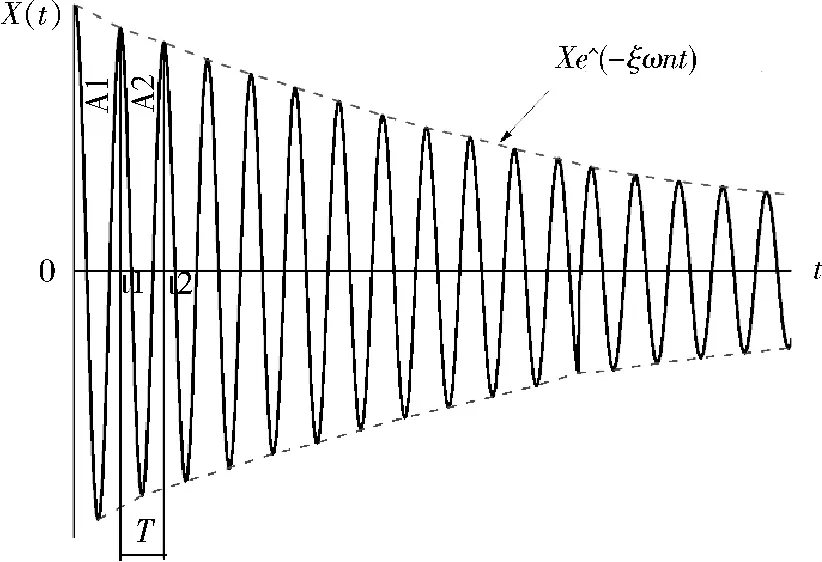
图3 自由振动衰减曲线Fig.3 Dampingcurve of free vibration

3 试验结果与分析

3.1 配气活塞头与气缸壁间的阻尼率

实验装置如图1所示，配气活塞由板弹簧支撑，其与气缸之间、与动力活塞内孔之间均采用间隙密封。为了测得配气活塞头与气缸壁间的阻尼率，实验装置中的一动力活塞拆除，以去掉配气活塞杆与动力活塞内部的阻尼影响。实验装置内抽成真空，以去掉气体工质的粘性阻尼影响。实验测得的配气活塞的速度与阻尼率的关系如图4所示。

由图4所知，配气活塞头与气缸壁之间的摩擦阻尼率在0.01至0.02之间。低速时摩擦阻尼率较大，随着配气活塞运动速度的增加，阻尼率急剧减小，在0.6 m/s之后逐渐趋于平稳。分析原因是在低速时，配气活塞头与气缸壁之间处于边界磨损状态，需要克服活塞启动时的静摩擦力，速度升高后，活塞头与气缸壁之间的微凹体之间形成动压润滑，摩擦率下降。

图4 配气活塞头与气缸壁间的阻尼率随活塞速度的变化曲线Fig.4 Damping ratio of displacer and cylinder wall changes with velocity

3.2 配气活塞杆与动力活塞内孔的阻尼率

该部分的实验装置与图1所示的装置结构相同，实验环境在真空下进行，这样测得的阻尼率是配气活塞头与汽缸壁间的阻尼率与配气活塞杆与动力活塞内孔的阻尼率之和。由于前面已经测得配气活塞头与汽缸壁间的阻尼率，用本实验测得的值减去配气活塞头与汽缸壁间的阻尼率的值，就可得到配气活塞杆与动力活塞内孔的阻尼率。图5给出了测得的配气活塞的速度与阻尼率的关系。

图5 配气活塞杆与动力活塞内壁间的阻尼率随活塞速度的变化曲线Fig.5 Damping ratio of displacer rod and inner wall of piston changes with velocity

由图5所知，配气活塞杆与动力活塞内壁的摩擦阻尼率也在0.01至0.02范围内。其变化规律也与图4所示的变化规律一致。低速时摩擦阻尼率较大，随着配气活塞运动速度的增加，阻尼率急剧减小，在0.7 m/s之后逐渐趋于平稳。

3.3 不同充气压力的阻尼率

该部分实验是给图1所示的实验装置中充入不同压力的气体工质，测得在不同充气压力下，气体工质的粘性率。与上一组实验相同，本实验测得的阻尼率实际上是配气活塞头与汽缸壁间的阻尼率、配气活塞杆与动力活塞内孔的阻尼率和气体工质的粘性阻尼率之和。所以，气体工质的粘性阻尼率需要用实际测量的数前面测得的两个值。本实验测得的配气活塞的速度与阻尼率的关系如图6所示。

图6 不同充气压力下的阻尼率随活塞速度的变化曲线Fig.6 Damping ratio changes with velocity at different charge pressure

由图6可知，在不同的充气压力下，配气活塞的阻尼率在0.04¯0.07范围内。低速时阻尼率较大，随着速度的增大，摩擦阻尼率逐渐减小。虽然由于测量误差的存在，每个充气压力下的阻尼率测量曲线都有波动，但依然可以看出，同一速度下，充气压力越大，阻尼率越大，但不同充气压力间的阻尼率差值很小。

3.4 不同热源温度下的阻尼系数

自由活塞斯特林发动机工作在高低温热源间，低温为常温，高温可达600℃以上。由于气体工质的粘性阻尼与压力、体积、温度等参数有关，所以，不同热源温度会对气体工质的粘性阻尼率产生影响。该部分实验是在充气压力为2 MPa的情况下，改变不同的热源温度，得到了不同热源温度下配气活塞的速度与阻尼率的关系，具体关系如图7所示。

由图7可知，在不同的热源温度下，配气活塞的阻尼率在0.075¯0.085范围内。与前面的运动规律一致，低速时阻尼率较大，随着速度的增大，摩擦阻尼率逐渐减小。同一速度下，热源温度越高，阻尼率越大，不同热源温度间的阻尼率差值同样很小。

图7 不同热源温度下的阻尼率随活塞速度的变化曲线Fig.7 Damping ratio changes with velocity at different hot source temperature

现将以上测得的各阻尼率进行对比，对比结果如图8所示。图8给出了配气活塞头与气缸壁之间、配气活塞杆与动力活塞内壁、实验装置充气压力2 MPa(不加热)和实验装置充气压力2 MPa(热源温度600℃)4种情况下的阻尼率随配气活塞运动速度的变化情况。由图可知，配气活塞头与气缸壁之间的摩擦阻尼率和配气活塞杆与动力活塞内壁之间的摩擦阻尼率都在0.01¯0.02之间，当实验装置充气2 MPa后，系统的阻尼率迅速增加，阻尼率的变化范围在0.4¯0.7之间，若此时再将热源温度升至600℃，系统的阻尼率会再次增加，阻尼率的变化范围在0.075¯0.085间。

图8 不同情况下的阻尼率随活塞速度的变化曲线Fig.8 Damping ratio changes with velocity at different condition

为了能够更直观地显示各部分阻尼所起的作用，图9给出了实验装置在充气压力2 MPa时，加入热源前后的各部分阻尼所占比例。图9(a)所示是加入热源前的比例关系图，图中配气活塞头与气缸壁和配气活塞杆与动力活塞内壁两处的摩擦阻尼率约占整个阻尼率的16%，气体工质引起的粘性阻尼约占整个阻尼率的67%。图9(b)所示是加入热源后的比例关系图，图中配气活塞头与气缸壁和配气活塞杆与动力活塞内壁两处的摩擦阻尼率占整个阻尼率的比例下降到13%左右，气体工质引起的粘性阻尼占整个阻尼率的比例上升到了74%左右。由此可见，当发动机配气活塞与气缸之间采用间隙密封时，配气活塞的气体阻尼尤其是加热热源后的气体阻尼起主导作用，而机械摩擦阻尼的作用较小。

图9 各部分阻尼率占总阻尼的比例Fig.9 Proportion of each damping ratio

4 结论

为了掌握自由活塞斯特林发动机的动力学特性，文章在配气活塞动力学模型的基础上，分析了动力学方程中阻尼项的组成。根据不同的组成项，设计了不同的阻尼测试实验方案。然后利用自由振动法，得到各阻尼项的阻尼率，具体结论如下:

(1)配气活塞头与气缸壁之间的摩擦阻尼率、配气活塞杆与动力活塞内壁的摩擦阻尼率均在0.01至0.02之间。低速时摩擦阻尼率较大，随着配气活塞运动速度的增加，阻尼率急剧减小，在0.7 m/s之后逐渐趋于平稳。

(2)在不同的充气压力下(0.5 MPa以上)，配气活塞的阻尼率位于0.04¯0.07范围。低速时阻尼率较大，随着速度的增大，阻尼率逐渐减小。同一速度下，充气压力越大，阻尼率越大，但不同充气压力间的阻尼率差值很小。

(3)在不同的热源温度下，配气活塞的阻尼率位于0.075¯0.085范围。低速时阻尼率较大，随着速度的增大，阻尼率逐渐减小。同一速度下，热源温度越高，阻尼率越大，不同热源温度间的阻尼率差值同样很小。

(4)处于一定充气压力中运动的配气活塞，气体阻尼起主导作用。加入热源前，配气活塞头与气缸壁和配气活塞杆与动力活塞内壁两处的摩擦阻尼率约占整个阻尼率的16%，气体工质引起的粘性阻尼约占整个阻尼率的67%;加入热源后，配气活塞头与气缸壁和配气活塞杆与动力活塞内壁两处的摩擦阻尼率占整个阻尼率的比例下降到13%左右，气体工质引起的粘性阻尼占整个阻尼率的比例上升到了74%左右。

1 ThombareD，Verma S.Technological development in the Stirling cycle engines［J］.Renewable and Sustainble Energy Reviews，2008，12(1):1-38.

2 贾红书.100W自由活塞斯特林发电机整机研制及性能分析［D］.北京:中国科学院.2011.JiaHongshu.Development of 100W free piston Stirling generator and the performance analysis［D］.Beijing:The PhD paper of University of Chinese Academy of Science.2011.

3 Sternlicht B.The stirling engine:prime mover of the 21stcentury［J］.Endeavour，1984，8(1):21-28.

4 Nie W，He J，Du J.Performance characteristic of a Stirling refrigeration cycle in micro/nano scale［J］.Physica A:Statistical Mechanics and its Applications，2009，388(4):318-324.

5 Budliger JP，Vdi VDI.Simple free-piston Stirling engine for combined power-thermal and refrigeration systems in households［C］.Advanced Energy Conversion and Application-Decentralized Energy Systems.2001:69-78.

6 杨尚平，吴张永，杨晓玉，等.粘性阻尼系数的动态测试法［J］.机床与液压，2005，(1):80-82.Yang Shangping，Wu Zhangyong，Yang Xiaoyu，Ma Junqi.The dynamic testing method of viscous damped coefficient［J］.Machine Tool and Hydraulics，2005，(1):80-82.

7 向 宇，匡 波，李 青，等.分置式斯特林制冷机排出器运动阻尼的在线辨识［J］.低温工程，1998，(2):22-36.Xiang Yu，Kuang Bo，Li Qing，GuoFangzhong.Identification of a Moving Damping of a Split Cycle StirlingCryocooler by On-line Method［J］.CRYOGEN ICS，1998，(2):22-36.