图像特征聚类优先级判定方法

王佳欣，彭天强，高毫林

(1.河南工程学院 计算机学院,河南 郑州 451191；

2.解放军信息工程大学 信息系统工程学院,河南 郑州 450002)



图像特征聚类优先级判定方法

王佳欣1，彭天强1，高毫林2

(1.河南工程学院 计算机学院,河南 郑州 451191；

2.解放军信息工程大学 信息系统工程学院,河南 郑州 450002)

摘要：由于图像多种特征的表述能力不同，所以它们在不同图像集上的聚类效果也不同.为确定在特定图像集上图像特征的聚类优先级，分析了3种全局特征颜色、纹理和形状的区分力，通过图像距离曲线说明了其区分力的不同，并通过检索结果验证了不同的区分力可导致检索结果的不同，进一步提出了由类紧致性和类分离性组成的判别指标——简化全局聚类质量.实验证明，区分性强的特征判别指标最好，该指标可用于确定图像聚类的优先级，从而决定聚类时选取图像特征的种类和图像特征选用的顺序.

关键词：图像聚类；聚类优先级；简化全局聚类质量

模式识别中的学习问题主要包括无监督学习(聚类)、有监督学习(分类)和半监督学习[1]，聚类为一组对象创建分组或类使得类内对象十分相似而类间对象非常不同.虽然人们已经提出了多种聚类算法，但聚类仍是一个具有挑战性的问题,一个聚类算法会因为数据机特征的选择和算法参数的不同而得出不同的聚类结果.

在图像处理和计算机视觉中，聚类主要是确定相似图像元素分组的过程，图像元素包括像素、图像分块、图像中的物体甚至完整的图像.其中,对图像的聚类是数据聚类的主要应用之一，它的目标是对图像集进行分组，使同一类的图像比不同类的图像更相似[2].文献[3]把图像聚类算法分为两类——有监督的和无监督的.有监督的聚类算法需要人为干预，也就是聚类前对图像进行标注，而这在在线应用中几乎是不可能的.由于不同的图像特征对图像的表述方式不同，所以它们的区分力会因图像内容的不同而不同.因此，在图像内容不同的图像集中，各特征的区分力也会不同，这就会导致聚类结果的不同.为了确定在特定图像集中聚类时采用特征的种类或者特征采用的优先级，需要对不同特征的优先级进行分析.与特征选择不同，特征选择主要是从特征中选取一定的维度也就是确定一个特征的子空间[4]；与特征组合也不同，特征组合通过对不同特征组合提高区分力[5].优先级判定是根据区分力对特征的聚类优先级进行判定，进而确定最适合聚类的特征.

本研究分析了不同图像特征，主要是颜色、纹理和形状的区分力，分别是颜色直方图、Gabor纹理和几何矩.为了直观地显示图像特征的区分力，给出了不同特征的图像距离曲线，不同特征的距离曲线和拟合曲线差异较大.还进行了图像检索实验，发现检索结果也有明显差异.为描述不同图像特征的区分力导致的检索结果的差异，定义了一个判别因子——SOCQ(Simplified Overall Cluster Quality)，该因子值的大小能反映对应图像特征聚类结果的好坏，可用来判断哪种特征更适合于聚类和各特征聚类优先级的高低.

1图像特征的区分力

为了便于计算，主要讨论图像的全局特征，最常用的图像全局特征是颜色、纹理和形状，这里分别使用HSV颜色直方图、Gabor纹理和几何矩.

1.1特征提取

因为每种特征都是图像信息的一种近似，不同特征体现不同的图像信息，所以对于同样的两幅图像，其相似程度在不同特征下得出的结果可能不同.

HSV颜色直方图是常用的图像颜色特征之一，它需要把彩色图像转换到HSV空间并进行量化.H，S和V的量化如下：

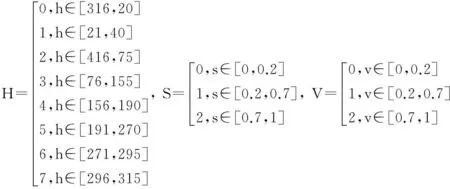
(1)

这3个分量的量化结果可以组合成一个变量：

x=9H+3S+V，

(2)

这里，x∈[0,71].这样，图像就可以用一个72维的直方图来表示.

纹理特征是基于Gabor函数和小波计算的.给定一幅图像I(x, y), 其Gabor小波变换定义如下：

(3)

式中，*表示共轭.假设局部纹理区域空间上相似，则可使用变换系数模值的均值μmn和标准差σmn来表示这个区域：

(4)

这样，图像特征就可以根据这两个值构造.实验使用的特征中设置尺度因子m = 5， n = 4，得出40维特征向量

(5)

形状特征使用几何矩进行描述，它将图像函数f(x,y)映射到xpyq的单项式上，x,y是图像的坐标.图像函数f(x,y)的(p+q)阶几何矩

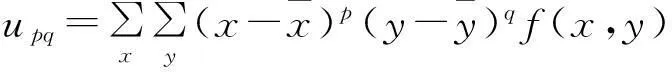
(6)

其中，p=0，1，2，…，∞,q=0,1,2,…,∞.

采用对平移、尺度和旋转具有不变性的7个不变矩，它们的性能在各种变形的情况下经过了验证,其定义如下：

m1=η20+η02,

m3=(η30-3η12)2+(3η21+η03)2,

m4=(η30+η12)2+(η21+η03)2,

m5= (η30-3η12)(η30+η12)[(η30+3η12)2-3(η03+η21)2]+

(3η21-η03)(η21+η03)[3(η30+η12)2-(η03+η21)2],

m6=(η20-η02)[(η30+η12)2-(η21+η03)2]+4η11(η30-η12)(η21+η03),

m7= (3η21-η03)(η30+η12)[(η30+η12)2-3(η03+η21)2]+

(3η12-η30)(η21+η03)[3(η30+η12)2-(η03+η21)2],

(7)

其中,ηpq=upq/(u00)γ并且p+q=2,3,…,γ=1+(p+q)/2.这7个矩可以组成一个特征向量f=(m1,m2,…,m7)来表征一幅图像.本实验使用的是25维向量：

(8)

1.2特征区分力

为了显示3种图像特征的区分力，从国际上普遍用于图像目标分类的Caltech256图像库中选择4类共100幅图像，每类25幅，记作图像集1.图像集1的3种特征的特征分量分布如图1所示.图中,横坐标代表的是特征分量，纵坐标代表的是特征分量值.可见，不同特征的特征分量分布图变化趋势相似，但近似程度仍有区别，也就是说不同特征的区分力不同.

图像距离对聚类算法相当重要，许多算法根据图像间的欧式距离对图像分组.为了便于直观显示，以第一幅图像为基准，给出了它与其他图像特征的欧式距离，如图2所示.

图1　图像集1的全局特征分量分布图Fig.1　The global feature curves for image dataset 1

图2　图像集1中第1幅图像与其他图像在不同特征下的欧式距离Fig.2　The distance between the first image andother images in image dataset 1 for global feature

由图可见，由于特征区分力的不同，3种特征的距离曲线的拟合曲线是不同的，这使得图像集中同一幅图像在不同特征情况下对于基准图像的相似度排名不同(距离越小，相似度越高，排名越靠前).为了直观地显示相似度排序，图3给出了以第1幅图像为检索图像的检索结果(结果中的第1幅图像即为检索图像). 图3(a)用颜色特征进行检索，图3(b)用纹理特征进行检索，这两幅图仅给出前30幅最相似图像的检索结果.可见，检索结果是有较大差异的.

图3　图像集1在不同特征下的检索结果Fig.3　The retrieval results of different feature for image dataset 1

因为不同特征的相对相似度可能不同，所以检索结果也会有所不同.为了确定聚类使用的最优特征或特征使用优先顺序，借助于聚类有效性分析方法进行判决.

2聚类有效性和OCQ(Overall Cluster Quality)

2.1聚类有效性

数据集特征选择和算法参数值的不同,会导致聚类算法的结果不同[6].从数据分布的观点看，聚类算法难以得出好的结果的一个重要原因是没有关于数据结构的先验信息.因此，聚类的准确性完全依赖于数据和聚类算法获取数据结构信息的程度.为了简化聚类算法，可以为数据集指定某种结构.例如，假设数据是高斯分布的合成，这样就可以通过EM算法解决问题.但是，如果假设的结果是错的，聚类结果也会很差.因此，使用某种目标测度以量化的方式对聚类结果进行评价是重要的，这就是聚类有效性分析.聚类有效性分析在模式识别中是一个主要的研究方向，它致力于发现数据集的分布、确定最合适的聚类算法和决定某一聚类方法的最优参数.

聚类有效性的判定主要有3种方法，第一种方法基于外部准则，它为数据集预先设置一种数据结构，在此基础上评价聚类结果；第二方法基于内部准则，它在数据集自身向量数量的基础上对聚类结果进行评价；第三种方法基于相关准则，也就是在和其他聚类方案比较的基础上进行评估，不同的聚类方案可以由同一算法的不同参数产生，也可以来自不同的聚类算法.前两种方法是基于统计检验的，主要缺点是计算量较高，而且它们主要衡量数据集与预先设置方案的吻合程度，但预先设置的方案未必是最合适的.

2.2Renyi熵和OCQ

好的聚类结果应该最符合数据集的分布，也就是说数据点分给哪个类与数据的内在结构吻合.这种思想在数学上可以用信息论来实现，也就是使用熵来衡量不确定度.常用的是Renyi熵[7]，其定义为

(9)

其中，pk是离散数据的概率集合函数.当α=2时，可得二次Renyi熵，也就是香农熵.当使用Parzen窗方法近似数据的概率函数时，有

(10)

这里，Gauss(·)是高斯函数，N是样本数量，V(x)是与样本间平方距离对应的指数衰减函数.

在相关准则的基础上，He等[8]根据Renyi熵提出了基于紧致性和分离性的聚类评价函数.紧致性描述了每个类的成员之间的靠近程度，分离性描述了各个类之间的靠近程度.

类紧致性由数据集的偏离性定义：

(11)

(12)

这里，k表示数据集X产生的类的数目，dev(Ci) 表示类Ci的偏差，dev(X)表示数据集X的偏差.

类分离性借助了文献[9]的思想和聚类评价函数的形式，其定义为

(13)

其中，σ是高斯常量.为简化计算，令2σ2=1，k是类数目，ci是Ci的中心，d(ci,cj)表示ci和cj中心的距离.

He用类紧致性和类分离性组合成总体聚类指标来评价聚类质量，其定义为

Ocq(X)=β·Cmp(X)+(1-β)·Sep(X),

(14)

其中,β∈[0，1]是类紧致性和类分离性的平衡因子，如Ocq(0.5)给两部分衡量相同的权重.

2.3简化OCQ(SOCQ)

由前述可见，Cmp(X)的值越小类紧致性越强，Sep(X)的值越小类分离性越强,即OCQ的取值随着类紧致性和类分离性的增加而单调递减.但是，由于Sep(X)中指数运算的计算复杂度较高，它设计的目的是反映类间距离的影响，同时与Sep(X)有相同的单调性.因此，可以设计一个新的简化的OCQ，它的Sep(X)不使用指数函数，仅保留类中心距离d2(ci，cj)，称作Simplified OCQ(即SOCQ).新的Sep(X)定义为

(15)

这时，Sep(X)随着类中心距离平方和的增加而单调增加.因此，为了不改变SOCQ的单调性，使它的两部分有相同的单调性，将SOCQ(X) 定义为

Ocq(X)=-β·Cmp(X)+(1-β)·Sep(X),

(16)

其中,β=0.5.因此，SOCQ随着类分离性和类紧致性的增加而单调增加，与OCQ的单调性相反.

3实验

从图3可以看出图像集1的3种特征区分性不同，纹理和形状特征的区分性不是十分明显，检索结果的准确率也不高.为构建区分性强的图像集，从TRECVID选择4类75幅图像构成图像集2，这4类图像分别来自于“compere”、“singer”、“rice” 和“sports”.对图像集2进行检索，结果见图4.查询图像为这两幅图中的第1幅图像.

图4　图像集2在不同特征下的检索结果Fig.4　The retrieval results of different feature for image dataset 2

从图4可以看出，颜色特征的检索结果要好于纹理特征.这说明对于该查询图像，颜色特征的区分性要好于纹理特征.同样，图5给出了第4类第1幅图像即第56幅图像与图像集2中其他图像的距离和各自的拟合曲线.可见，图中的距离曲线有明显的阶跃.与图2相比，该图的阶跃更加明显，这说明该图像集的类间距离更大.

图5　图像集2中第56幅图像与其他图像的距离Fig.5　The distance between the 56th image and other images for image dataset 2

同时，图5中3种特征的阶跃程度也不同，前两者高于后者，这说明第3种特征的区分性最弱.为计算聚类结果的OCQ值，对图像集2采用k-means算法进行聚类并重复20次，结果见图6(a).可见，形状特征的OCQ因子最大、颜色特征最小，这说明颜色特征聚类的结果最好、形状特征最差.类似地，计算该聚类结果的SOCQ因子值，结果见图6(b).3种特征因子值的大小关系与图6(a)相比是相反的，但反映的聚类效果相同，即颜色特征的聚类效果最好、形状特征的聚类效果最差.

图6　图像集2的OCQ和SOCQ因子的值Fig.6　The OCQ and SOCQ of image dataset 2

4结语

为判定在特定图像集上哪种特征更适合于聚类，提出了描述特征区分力的判别因子——SOCQ，用它来确定图像特征聚类的优先级.SOCQ值高的图像特征聚类优先级高，更适合于聚类，因为该特征的区分性更强.SOCQ与OCQ的不同不仅在于它的计算复杂度低，还在于它可以在聚类之前进行计算，这也是它与聚类有效性分析不同的地方.如果需要使用多种特征进行聚类，可将SOCQ值高的特征赋予较高的优先级.

参考文献：

[1]ChapelleO,ScholkopfB，ZienA.SemisupervisedLearning[M].Cambridge：MAMITPress，2006.

[2]JainAK,MurtyMN,FlynnPJ.Dataclustering:areview[J].ACMComputingSurveys,1999，31(3):264-323.

[3]KrinidisS,KrinidisM，ChatzisV.AnunsupervisedimageclusteringmethodbasedonEEMDimagehistogram[J].JournalofInformationHidingandMultimediaSignalProcessing，2012，3(2):151-163.

[4]QinBS,JingJN,WangGT.Afastclustering-basedfeaturesubsetselectionalgorithmforhigh-dimensionaldata[J].IEEETransactionsonKnowledgeandDataEngineering,2013，25(1):1-14.

[5]TrungTN,ZhuRL,SilanderT,etal.Onlinefeatureselectionformodel-basedreinforcementlearning[C]∥Proceedingsofthe30thInternationalConferenceonMachineLearning.Atlanta：[s.n.],2013.

[6]苑玮琦，谷宗辉.全手掌纹5类主线特征选择方法研究[J].仪器仪表学报,2012,33(4):942-948.

[7]MichaelJA,Berry,LinoffG.DataMiningTechniquesforMarketing,SalesandCustomerSupport[M].NewYork:JohnWiley&Sons,1996.

[8]HeJ,TanAH,ChewLT.Modifiedart2Agrowingnetworkcapableofgeneratingafixednumberofnodes[J].IEEETransactionsonNeuralNetworks,2004(15):728-737.

[9]GokcayE,PrincipeJ.AnewclusteringevaluationfunctionusingRenyi’sinformationpotential[C]∥ProceedingsoftheInternationalConferenceAcoustic,Speech,SignalProcessing.Istanbul:[s.n.],2000.

Cluster priority level decision method for image features

WANG Jiaxin1, PENG Tianqiang1, GAO Haolin2

(1.CollegeofComputerScienceandEngineering,HenanInstituteofEngineering,Zhengzhou451191，China；

(2.InstituteofInformationSystemEngineering,InformationEngineeringUniversity,Zhengzhou450002,China)

Abstract:Because of the different distinguishing ability for different features, the image cluster effects are also different for different image dataset. To decide cluster priority level of different features for one specific image dataset, we analyzed the distinguishing ability of three typical image features color histogram, Gabor texture and geometric moment, and showed the difference of the distinguishing ability among three global image features through their distance curves, and verified the difference of the distinguishing ability among three global image features through their different retrieval results. Based on the analysis, we presented a cluster discriminant index called Simplified Overall Cluster Quality, which is composed of two parts, cluster compaction part and cluster separation part. The experiment results showed that the feature with best distinguishing ability also possesses best discriminant index. So, this index can be used to decide the best feature which can be used to cluster images or the priority of features used for cluster.

Key words:image cluster; cluster priority level; simplified overall cluster quality

作者简介：王佳欣(1983-)，男，河南洛阳人，讲师，主要从事计算机应用方面的研究.

基金项目：国家自然科学基金(61301232);河南省教育厅科学技术研究重点项目(14A520066)

收稿日期：2014-11-12

中图分类号：TN391.4

文献标志码：A

文章编号：1674-330X(2015)01-0070-07