分组级短码长LT喷泉码的工程应用
2015-12-22张涛,王泽林
分组级短码长LT喷泉码的工程应用
张 涛1,王泽林2
(1.91655部队,北京100036;2.96219部队,广东清远511533)
针对LT喷泉码在准单向链路、高差错、链路恶劣易中断的信道环境应用时出现的运算量大、译码时延长、编码效率较低等问题,文章提出使用基于数据分块的分组级短码长喷泉码方案。其思想是将短码长LT码方案和分组级LT码方案结合起来,并且在数据子块的度序列生成过程中加入度值检测机制。实验仿真结果表明:与已提出的LT码方案相比,该方案能够有效地降低译码开销、计算代价和译码时延,提高系统的最大传输效率。
喷泉码;短码长;度值检测
近年来,随着我国航天和海洋技术的发展,深空通信、水声通信受到广泛关注。这2种通信场景面临相似的挑战[1]:传输时延大;前向与反向链路速率不对称;误码率和丢包率大。为克服这些问题,实现可靠传输,须要采用相应的传输编码技术。
文献[2]提出了利用喷泉码方案来解决深空通信面临的上述问题,文献[3]提到了采用纠错码的无记忆高斯信道可以等效为删除信道。文献[4]在忽略分组额外开销和链路误比特率为10-6的实验条件下采用喷泉码方案时,选取较短的分组来传输数据文件,以获得较高的成功概率。
本文针对上述恶劣通信环境下LT喷泉码码的工程应用问题展开研究,提出了使用基于数据分块的分组级短码长LT码方案。与传统LT码方案相比,在额外冗余信息(包头、包号、校验码等)不能忽略的情况下,系统的传输性能得到了较大的提高。
1 喷泉码技术
数字喷泉概念由M.Luby等人在1998年提出[5]。喷泉码的编译码过程可概括为:由k个信息分组生成无限多的编码分组,而用户只要接收到其中任意k(1+ε)个编码分组,即可通过译码以高概率成功恢复全部原始数据分组,其中ε是开销。
第一个实用的喷泉码——LT码[6]是在2002年由Luby等人提出的。LT码以其良好的性能和简单的编译码方法受到学术界和工业界的广泛关注。
1.1 Robust经典算法
LT码喷泉码的编译码性能直接由度分布函数决定,LT码Robust度分布函数[6]μ(d)定义为:
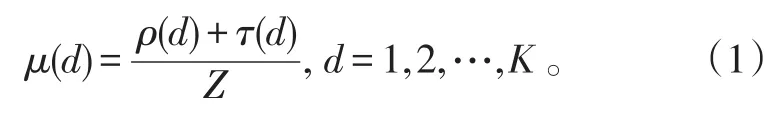
式(1)中:ρ(d)为理想孤子分布,是度数值为d的概率,且
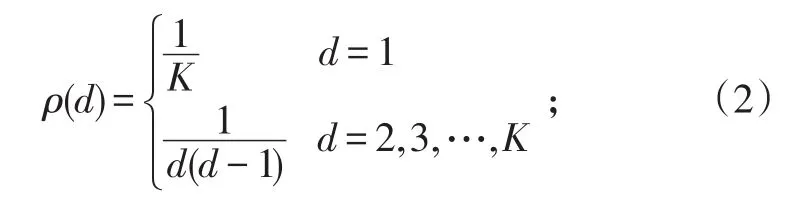
τ(d)为补充函数,表达式为
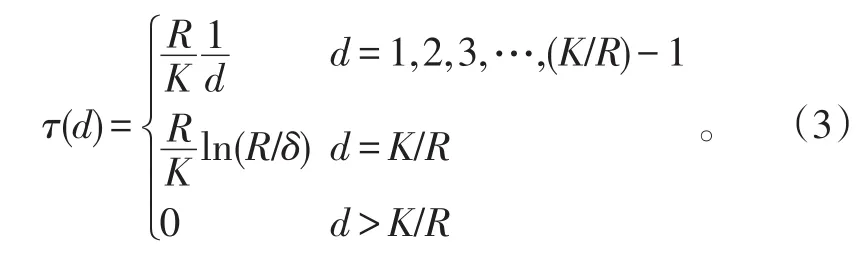
为获得良好的性能,经典LT喷泉码码长要达到104或者更高的量级[7-8]。这使得该编码方案在某些应用场合下使用具有局限性。
1.2 短码长LT码
为进一步提高LT码的实用性,文献[7,9-11]对短码长LT码进行了研究。对短码长的分析,文献[9-10]算法目前只有理论上的意义;文献[11]提供了最优化方法来计算短码长度分布,但局限于码长极端(10以内)的情况[7]。文献[7]提出的一种编码度分布函数的改进设计方法,得到了103量级的短码长喷泉码,扩展了喷泉码的应用。如果将103量级的短码长应用在链路误比特率为10-3环境中使用,基于信息分组数量K的度序列随机生成方案,亦会产生相对较大的度值以保证良好的覆盖率,这样含有冗余信息的编码分组的丢包概率较大,因而文献[7]设计的10-3量级的短码长在通信质量恶劣的环境中使用效果欠佳。
2 信道模型假设
为使问题分析起来简单,假设随机错误是导致分组“删除”的唯一原因,不考虑其他因素[4]。设链路误比特率为e,则每个编码分组的丢失率q可以表示为:
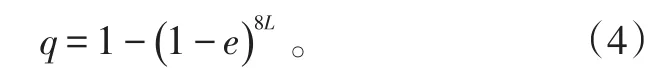
N为待传输文件长度,d为信息包长,L为编码分组的包长(包括信息分组,也包括包头、包号、校验码等冗余信息),K=ceil(N/D)为原始信息分组数量。图1为不同信道质量(误码率)下对应的丢包率。

图1 不同信道质量下的丢包率Fig.1 Package loss rate of different channel quality
利用喷泉码的无码率特性,使发送端以适应优质信道的参数条件来进行喷泉码的发送。在信道质量良好下,此方案可收到较好的传输效果。然而实际信道却多是时变的,甚至有时信道的质量相当恶劣,如图1所示,在误比特率为10-3时,以优质信道方案(一般数据包较长)进行传送数据,恶劣的信道质量会导致编码分组的丢包率较高,那么系统为完成译码而不得不接收更多的编码分组来弥补丢包率带来的“包丢失”,这样系统的传输效率就会非常低下。另外,如果采用较短信息分组来切割原始数据文件,那么会得到较大的信息分组数量K,而按照原有LT码方案进行编码,那么会得到冗余信息较多的编码分组。同样,较长的编码分组在恶劣信道下的丢包率也会很高。
3 基于数据分块的分组级短码长LT码解决方案
本文放宽了对度分布函数的优化要求,采用基于数据分块的分组级短码长LT码设计,方案如下。
首先,根据实际信道传输统计数据将信息分组长度划为24 Byte,将原始数据切割成子数据块长度在1 024~2 048 Byte之间(亦可根据信道状态进行相应长度划分);然后,对每个子块进行短码长LT码编码生成编码分组;接着,这些编码分组通过无线信道传输后,被接收端接收并参与译码;最后,将译码成功的子数据块进行拼接,完成编译码过程。对数据子块进行短码长度序列产生的流程图见图2。
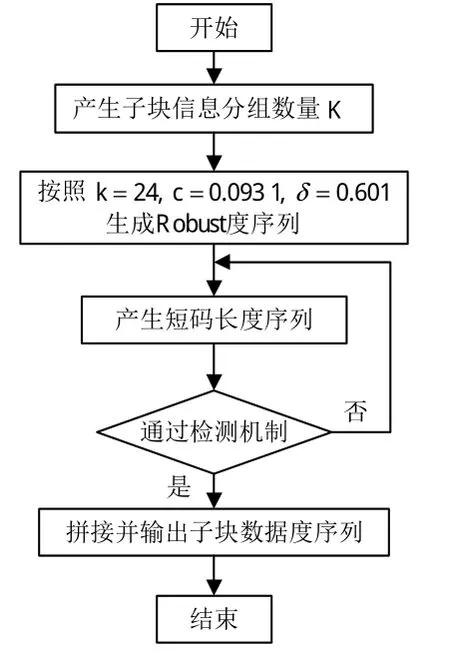
图2 子块数据短码长度序列产生流程图Fig.2 Flow chart of short code degree sequence generation with sub block
Robust度分布函数是一种通用的设计,可以改变其中的参数来适应不同的通信需求,本文采用的Robust度分布函数的参数为c=0.093 1,δ=0.601和式(2)中K=24。目的是为了取消大度值对信息分组的覆盖,以降低迭代次数,减小运算量。图3是Robust度分布函数在参数c=0.093 1,δ=0.601和K=24时产生子块数据短码长序列的度概率分布图。

图3 分组级短码长LT码方案采用的度概率分布Fig.3 Probability distribution of pack level short LT block codes
研究短码长度序列时发现:度函数序列的产生是遵循度分布函数规律的一个随机过程,度序列中度1的比重及其在译码迭代过程中是否能够持续产生,这直接决定着LT译码能够成功。无论是实用的Robust度分布或者其他改进的度分布函数,如开关度分布[12]产生的度序列,随机不确定因素使得在理论上性能优良的度分布函数也无法确保每次生成的度序列中度1所占的比重能达到相应的概率要求。表1为Robust和二进制指数度分布函数在采用不同的随机种子分别重复104次的度序列产生实验中度1概率不合格的概率。按这些度序列生成的编码分组通过删除信道后,被送到接收端来参与译码的失败率较高。Robust度分布函数特别是在短码长的应用中,度1的产生概率很低(低于10%,很多情况下,甚至无度1产生),而且还要通过信道的删除作用。因此,基于Robust度分布函数的短码长在恶劣信道中的有效性欠佳。

表1 不同的度函数产生序列中不合格度1的比重信息Tab.1 Speeific gravity information of sequence unqualified degree 1 with different degree function
鉴于度1分组的重要性,本文在不改变度分布函数的基础上,加入度1检验机制(见图2),只允许度1分组数量合格的度序列进入编码过程,以提高编码分组参与译码的有效性。
4 仿真分析
为便于本文方案和原始LT码方案的对比,引入参数:①开销ε[13];②计算代价(Dmean-1)×D×N,区别于文献[13],计算代价表达了信息分组字节长度D、开销ε和节点平均度Dmean之间的一个权衡,是异或运算进行的操作数;③传输效率η[14];④完成编译码所耗时间t。
图4是采用带检测机制的本文方案和已提出的LT码方案在开销、传输效率、计算代价和编译码时间的比较。原始数据长度为1 024~9 216 Byte,链路误比特率为10-3。经典LT码的Robust参数为c=0.03,δ=0.5,这个参数设置和文献[2-3]相对应。仿真平台是WindowsXP操作系统,CPU为3.0 GHz,内存2 GB,仿真工具Matlab7.8.0,以不同的喷泉码方案发送不同长度的源数据,分别重复1 000次取均值。

图4 本文提出的分组级短码长方案和经典LT码的性能对比Fig.4 Performance comparison of proposed short LT code and classical LT code
从图4中可以看出,随着原始数据长度的增长,已提出的LT码方案的计算代价和编译码时间的增长非常大,而带检测机制本文方案的计算代价和编译码时间增加相对较慢;无论是开销和传输效率带检测的本文方案均优于已提出的LT码方案,而不带检测机制方案的性能介于两者之间。值得注意的是,在源数据长度较小,或信息分组数量不大时,随机度序列具有较高的不合格率,接收端不得不接收更多的分组来保证译码成功,因而导致系统的译码开销和传输效率的波动较大。这说明,检测机制的引入能够提高短码长LT码编码分组的有效性。
仿真结果说明带检测机制的基于数据分块的分组级短码长LT码是可行而且实用的。借助Robust度分布函数的通用性,可为工程应用提供较为方便但不是最优的度分布函数[13]。原因是实际工程中原始数据不可能被分为无限个信息分组;LT码进行一次的编译码行为也不能与精准的数学理论分析相匹配;即使具有优化结构的度分布产生的编码分组经过信道而丢失部分分组后,会导致优化的编码分组构成被破坏。
5 结论
本文针对LT喷泉码实际工程应用,对基于数据分块的分组级短码长LT喷泉码进行了研究,仿真表明,在打破了信息分组数量K的束缚后,能够在误比特率10-3的信道条件下,使得开销、最大传输效率、计算代价和编译码时间4个方面的性能均优于现有LT码方案。本文的数据分块和信息分组的长度是大量实验所得的经验数据。下一步的研究将着眼于如何改进数据分块和信息分组的长度切割,以使得基于数据分块的分组级短码长喷泉码的性能趋向最优化。
[1]周辉,郑海昕,徐定根.空间通信技术[M].北京:国防工业出版社,2010:12-13. ZHOU HUI,ZHENG HAIXIN,XU DINGGEN.Space communication technology[M].Beijing:Defense Industry Press,2010:12-13.(in Chinese)
[2]李晖,姚文顶,张乃通.深空通信中的喷泉编译码技术[J].电讯技术,2008,48(4):8-12. LI HUI,YAO WENDING,ZHANG NAITONG.Fountain codes in deep space communication[J].Telecommunication Engineering,2008,48(4):8-12.(in Chinese)
[3]臧求实.喷泉码技术的研究[D].南京:南京邮电大学,2011. ZANG QIUSHI.Research on fountain codes technology [D].Nanjing University of Post and Telecommunication,2011.(in Chinese)
[4]姜博,曹志刚,晏坚.PLFEC可靠组播解决方案分组长度研究[J].清华大学学报,2008,48(4):567-570. JIANG BO,CAO ZHIGANG,YAN JIAN.Packet lengths of PLFEC-based reliable multicast solutions[J].Journal of Tsinghua University,2008,48(4):567-570.(in Chinese)
[5]BYERS J W,LUBY M,MITZENMACHER M,et al.A Digital fountain approach to reliable distribution of bulk data[C]//Proceedings ofACM Sigcomm’98.1998:56-67.
[6]LUBY M.LT codes[C]//IEEE Symposium on Foundations of Computer Science.2002,16(19):271-282.
[7]朱宏杰.喷泉码编译码技术与应用研究[D].北京:清华大学,2008. ZHU HONGJIE.Research on codec technology and applications of fountain codes[D].Tsinghua University,2008.(in Chinese)
[8]MACKAY D J C.Fountain code[J].IEEE Proceedings on Communications,2005,152(6):1062-1068.
[9]KARP R,LUBY M,SHOKROLLAHI A.Finite length analysis of LT codes[C]//IEEE International Symposium on Information Theory.2004:37-39.
[10]MANEVA E,SHOKROLLAHI A.New model for rigorous analysis of LT-codes[C]//IEEE International Symposium on Information Theory.2006:2677-2679.
[11]HYYTIA E,TIRRONEN T V J.Optimal degree distribution for LT codes with small message length[C]//International Conference on Computer Communications.2007:2576-2580.
[12]雷维嘉,刘慧峰,谢显中.开关度分布:一种改进的LT数字喷泉编码度分布[J].重庆邮电大学学报,2012,24(1):34-38. LEI WEIJIA,LIU HUIFENG,XIE XIANZHONG. Switch degree distribution:an improved degree distribution for LT digital fountain code[J].Journal of Chongqing University of Posts and Telecommunications,2012,24(1):34-38.(in Chinese)
[13]CHEN CHIHMING,CHEN YINGPING,SHEN TZU CHING.Optimizing degree distributions in LT codes by using the multiobjective evolutionary algorithm based on decomposition[C]//Proceedings of Evolutionary Computation.2010:1-8.
[14]ROY BLAKE.现代通信系统[M].2版.北京:电子工业出版社,2003:321-322. ROY BLAKE.Electronic communication systems[M]. Beijing:Publishing House of Electronics Industry,2003:321-322.(in Chinese)
Practical Research on Short Block Length Packet-Level LT Codes
ZHANG Tao1,WANG Zelin2
(1.The 91655thUnit of PLA,Beijing 100036,China;2.The 96219thUnit of PLA,Qingyuan Guangdong 511533,China)
In quasi unidirectional links,poor channel environment and high error rate situations,LT fountain codes often cause a large amount of computing,extended decoding time,low coding efficiency and other problems.In this paper,the small code length packet-level coding scheme was proposed,which combined the short block length coding and packetlevel LT codes,and applying degree detection mechanism in the process of sequence data generated in the sub-blocks. The simulation results showed that compared with the conventional LT codes,the proposed scheme could effectively re⁃duce the cost of decoding,computing costs and decoding delay and increase the maximum transmission efficiency of the system.
LT codes;short blocke length;degree detection
TN919.8
A
1673-1522(2015)05-0433-04
10.7682/j.issn.1673-1522.2015.05.007
2015-07-05;
2015-08-15
张 涛(1977-),男,工程师,硕士。
