基于分层组合法推导钢骨－钢管高强混凝土抗弯承载力

陈兰响，关 萍

（大连大学 建筑工程学院，辽宁 大连116622）

钢骨－钢管高强混凝土组合构件是将型钢放入钢管中，然后内填高强混凝土浇筑而成的新型组合结构形式。对钢骨－钢管高强混凝土的研究结果[1－3]表明，钢骨的存在有效地增加了组合柱的抗压性能和抗震性能。钢骨－钢管混凝土的力学性能较多，有短柱轴压力学性能、长柱失稳和压弯性能等，研究纯弯力学性能是研究长柱失稳、压弯性能和抗震性能的前提。

目前，大连理工大学王清湘教授、赵大洲博士，以及东北大学王连广教授都对钢骨－钢管混凝土的纯弯力学性能[4]进行了部分理论和试验研究，分析了影响组合柱抗弯力学性能的因素，基于各自分析的影响因素和方法，建立出钢骨－钢管高强混凝土的抗弯承载力计算公式。

本文拟基于截面分层组合法[5－7]，汇编了钢骨－钢管混凝土构件处于纯弯状态下的非线性分析程序，对影响其抗弯性能的各种因素进行了分析，找出影响其力学性能的关键指标，同时基于“钢管混凝土统一”理论建立其抗弯承载力公式。

1 理论研究

1.1 研究假设

（1）截面的轴向变形呈线性分布，且应变应符合平截面假定。

（2）钢材与混凝土之间粘结良好，不出现滑移。

（3）组合构件的变形不受剪力的影响。

（4）钢材的受拉、压应力－应变关系模型[8]采用4个阶段，见图1。

图1 钢材的σ－ε曲线

图1 中，fu、fy为钢材的屈服应力和强化极限应力，fu＝ （1.4～1.6）fy；ε0和ε1分别为钢材刚进入屈服时的应变和屈服末的应变，ε2为强化极限fu对应的应变，ε1＝10ε0、ε2＝100ε0。

（5）圆钢管内核心混凝土的受压应力（σ）－应变（ε）关系模型见式（1）[1]:

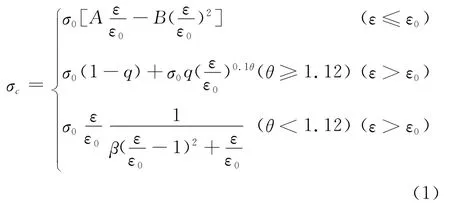
其中，

式中:fcu为立方体的抗压强度；At和As分别为钢管和钢骨材料的面积；ρ为配骨率；θ为套箍率。

混凝土的受拉应力（σ）－应变（ε）关系模型见式（2）[8]:

1.2 计算原理与步骤

对于钢骨－圆钢管混凝土受弯构件，采用截面分层法计算模型，见图2。

图2 计算模型

钢骨－钢管混凝土在弯矩作用下，设已知曲率为φ，由平截面假定可得到截面上任意一点应变为:

式中:ε0为截面形心处的应变；yk为计算点坐标。

将钢管截面划分成2n等份，x轴以上的每段对应的圆心角、形心高度和面积为:

将混凝土截面划分成2m份，x轴以上每段对应的高度、形心位置和面积为:

其中，xsi为型钢第i（i＝Ⅰ，Ⅱ…Ⅴ）区段对应的宽度。

将钢骨截面划分为接近二倍高度的整数倍，用2[h]表示，则每段对应的高度、形心位置和面积为:

对于x轴以下各材料区段的命名及参数的取值同理亦可求得。

由此可得到内轴力和内弯矩:

对于纯弯曲状态，应保证轴力:

具体步骤为:在给定截面曲率φ的情况下，通过调整形心处的应变ε0，使得内轴力N小于某一接近于0的数值时，确定形心处应变，计算得到截面弯矩。

2 参数分析

根据分层截面分层方法的理论，利用Matlab软件编制了钢骨－钢管高强混凝土纯弯力学性能的分析程序，计算弯矩M在钢材强度、混凝土强度和钢管壁厚等参数下的曲率φ的变化值。

选取文献[1]中试件HC10－0为参考构件，其混凝土立方体强度fcu＝74.3MPa，钢管直径D＝218mm，壁厚t＝4.0mm，钢骨面积As＝2 314 mm2，钢骨惯性矩Is＝2 085 759mm4，钢管的屈服强度为269MPa，钢骨的屈服强度为288MPa。

2.1 混凝土强度

利用编制的钢骨－钢管高强混凝土纯弯非线性程序计算了不同混凝土立方体强度下强度的M－φ过程曲线，计算结果见图3。

图3 不同混凝土立方体强度下的M－φ曲线

由图3可知:钢骨－钢管混凝土的混凝土立方体抗压强度对构件的抗弯刚度和正常使用阶段的抗弯承载力影响很小，这与混凝土立方体强度对钢管混凝土的纯弯力学性能影响规律相似[8－10]。

2.2 钢材强度

利用编制的钢骨－钢管高强混凝土非线性分析程序计算了不同钢管屈服强度和不同钢骨屈服强度的弯矩M－曲率φ全过程变化曲线，计算结果分别见图4和图5。

图4 不同钢管屈服强度下的M－φ曲线

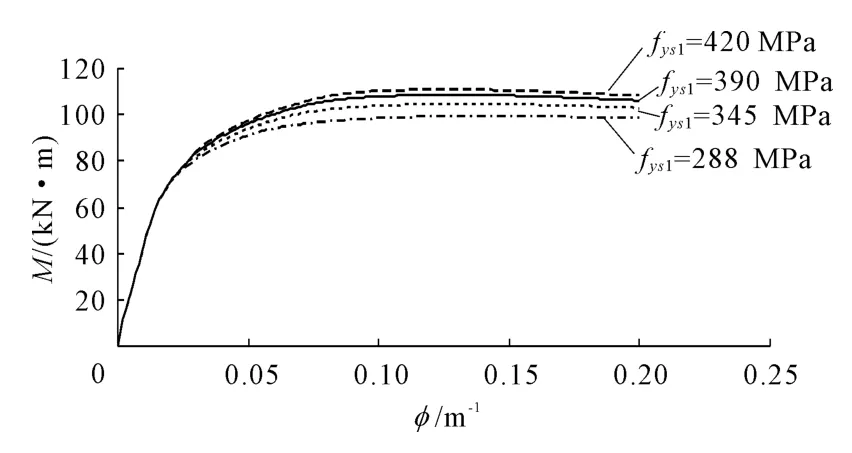
图5 不同钢骨屈服强度变化的M－φ曲线

由图4和图5可知:不同的钢管和钢骨的屈服强度对钢骨－钢管高强混凝土纯弯构件的抗弯刚度基本无影响，但组合构件的抗弯承载力随钢管和钢骨的强度的增大而提高，但钢管的屈服强度对其影响更大，这主要是由于钢管包围在四周，其惯性矩较大，所起的抗弯作用也就越大。另外，钢管和钢骨的屈服强度变化对钢骨－钢管高强混凝土构件在受弯下的延性性能无明显影响。

2.3 钢管壁厚

利用编制的钢骨－钢管高强混凝土纯弯非线性分析程序计算了组合构件在不同钢管壁厚下的弯矩M－曲率φ的全过程变化曲线，计算结果见图6。

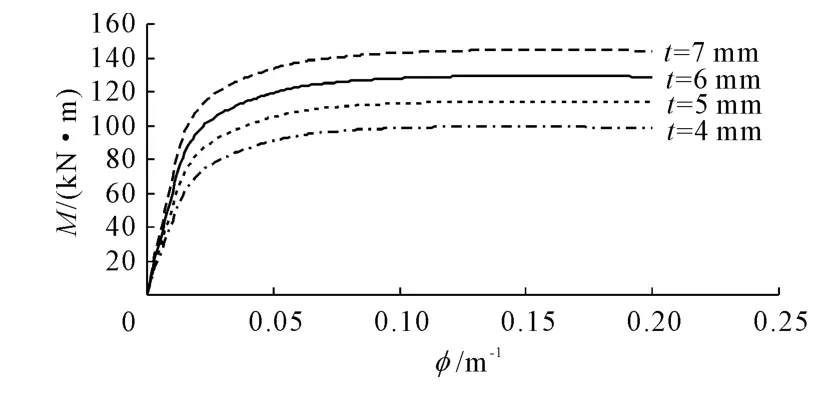
图6 不同钢管壁厚变化的M－φ曲线

从图6可知，随着钢管壁厚的增加，钢骨－钢管高强混凝土构件的截面面积和抗弯截面惯性矩均增大，抗弯刚度和抗弯承载力都明显提高，与钢管混凝土中钢管管壁厚度的影响规律类似[11－13]，这与提高钢管的屈服强度对抗弯承载力的作用形式是不同的。因此，在实际工程应用中，为提高组合构件的抗弯承载力，且在套箍率（θ）一定时，应尽量增加钢管的壁厚。

2.4 钢骨截面惯性矩

利用程序非线性分析程序计算了不同钢骨截面惯性矩下的弯矩M－曲率φ下的全过程曲线，计算结果见图7。

图7 不同钢骨截面惯性矩下的M－φ曲线

由图7可知，在钢骨－钢管高强混凝土的直径相对较小情况下，改变钢骨的截面惯性矩对初始刚度和抗弯承载力的影响较小；若在钢管的直径较大和含钢量不变的情况下，应尽量加大钢骨的截面高度来提高抗弯承载力和抗弯刚度。

3 抗弯承载力公式推导

虽然利用截面分层法可以很好地计算出钢骨－钢管高强混凝土的抗弯承载力，但这种方法不便于工程人员应用，故需要建立简洁且便于实际工程应用的抗弯承载力计算公式。

本文以“钢管混凝土的统一理论”[14]为基础，结合文献[4]中提出的钢骨－钢管轴压组合短柱的组合强度fscsy，并利用程序STSRHCZTF对fcu＝50 MPa～90MPa，fty，fsy＝235MPa～550MPa，θ＝0.025～3，ρ＝0～1范围内构件的承载力进行大量的计算，取钢管受拉区最外缘应变εmax达0.01对应的弯矩为抗弯承载力Mcal[15]，对结果进行回归分析，得出抗弯承载力计算公式:

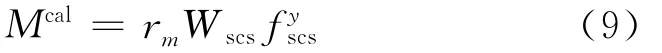
式中:Wscm为钢骨－圆钢管混凝土截面的抗弯模量，Wscm＝πD3/32；fscsy为组合短柱的轴心抗压强度，按式（10）计算；rm为截面塑形发展系数，通过对数值结果的回归，其计算公式按式（11）计算。

式中，

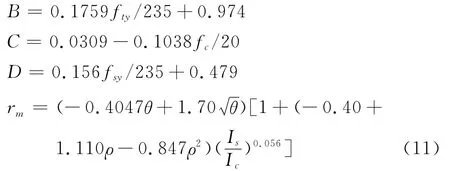
式中:Is和Ic分别为钢骨和混凝土横截面的惯性矩，Ic＝πd4/64－Is，d为钢管的内直径，t为钢管壁厚。

4 试验验证

将文献[1]中试件HC10－0和试件HC12－0，以及文献[3]中试件CW1和试件CW2的试验数据分别输入非线性分析程序和抗弯承载力计算式（9）～式（11），分别得到抗弯承载力程序计算值（Mmod）和简化公式计算值（Mcal），并于试验值（Mexp）对比，结果见表1。

表1 不同方法下的抗弯承载力比较

由表1可以看出，数值结果和简化公式计算值与试验结果较为吻合，又由文献[1]中知，试件HC10－0和HC12－0对应弯矩值出现误差的主要原因是构件在试验中的两端约束过大所造成的；本文中提出的抗弯承载力公式简单且适合在工程中应用。

5 结 论

（1）基于编制的非线性分析程序对影响钢骨－钢管高强混凝土抗弯力学性能的主要参数进行分析，可知套箍指标（钢管壁厚和钢管强度）的变化对承载力的影响较大，且钢管壁厚的增加还可以提高正常使用阶段的抗弯刚度。

（2）利用数值分析结果且基于“钢管混凝土统一理论”，建立了钢骨－钢管高强混凝土纯弯构件的抗弯承载力计算公式，通过与试验结果进行对比，吻合良好，可为钢骨－钢管高强混凝土的抗弯承载力计算提供参考。

[1]赵大洲.钢骨－钢管高强度混凝土组合柱力学性能研究[D].大连:大连理工大学，2003.

[2]关 萍，王清湘，赵大洲.钢骨－钢管高强度混凝土受弯组合柱的试验研究[J].地震工程与工程震动，2003，23（2），57－60.

[3]王清湘，赵大洲，关 萍.钢管－钢骨高强混凝土轴压组合柱受力性能的试验研究[J].建筑结构学报，2003，24（6）:44－49.

[4]刘 晓，王连广，王 兵.钢管钢骨高强混凝土抗弯构件试验研究[J].哈尔滨工业大学学报，2010，42（10）:1651－1655.

[5]Guan P，Chen L X.Influence of load condition on flex－ural properties and shear properties of steel tubular columns filled with steel－reinforced concrete[J].Applied Mechanics and Materials，Trans Tech Publications，Switzerland，2014，638－640:127－131.

[6]丁发兴，余志武.圆钢管自密实混凝土纯弯力学性能[J].交通运输工程学报，2006，6（1）:63－68.

[7]Roeder C W，Leham D E，Bishop E.Strength and stiffness of circular concrete－filled tubes[J].Journal of Structural Engineering，2010，（12）:1545－1553.

[8]张 岚.方钢管混凝土压弯构件截面非线性分析[J].工业建筑，2013，43（5）:132－136.

[9]韩林海，陶 忠.现代组合结构和混合结构－试验、理论和方法[M].北京:科学出版社，2009.

[10]赵同峰，王连广.方钢管－钢骨高强混凝土抗弯承载力分析[J].工业建筑，2008:38（3）:27－30.

[11]赵艳艳，吴乃森，王元生，等.矩形钢管混凝土梁的抗弯承载力仿真分析[J].计算机仿真，2011，28（9），382－385.

[12]卢 辉，韩林海.圆钢管混凝土抗弯刚度计算方法探讨[J].工业建筑，2004，34（1）:1－5.

[13]王 刚，钱稼茹，林立岩.钢管混凝土叠合构件受弯性能分析[J].工业建筑，2006，3（2）:68－71.

[14]韩林海.钢管混凝土结构[M].北京:科学出版社，2000.

[15]钟善桐.钢管混凝土结构（第三版）[M].北京:清华大学出版社，2003.