潜标上浮过程中垂直运动数学建模与验证*



潜标上浮过程中垂直运动数学建模与验证*

郭永青1，李小龙2，熊学军1,3*

(1. 国家海洋局 第一海洋研究所，山东 青岛 266061；2. 中海石油深海开发有限公司，

广东 深圳 518067； 3. 海洋环境科学和数值模拟国家海洋局重点实验室，山东 青岛 266061)

摘要：以2014年南海北部陆坡M站春、秋两季底流观测潜标回收为例，建立数学模型分析潜标上浮过程中垂直运动特征。首先做出忽略水平海流影响、刚性连接以及主要部件外形简化等假设。通过刚性连接部分上浮数值试验，得到释放后各部件能够保持相对位置不变、整体上浮的结论。视整个系统为刚体建立了垂直运动模型。分别模拟两次潜标回收，模型与高精度超短基线观测结果的对比表明：整个上浮过程可分为加速上浮阶段和稳定上浮阶段；模型速度曲线与观测速度拟合线比较接近，给出的平均模型速度与平均观测速度均相差0.2 m/s；模型能够反映出在稳定上浮阶段，稳定上浮速度随时间缓慢降低的变化特征；各部件上浮的垂直速度是振荡变化的。模型可为相关水下仪器回收工作提供定量化依据。

关键词：潜标回收；潜标垂直运动；数学建模；数值计算；高精度超短基线

潜标观测是深海海洋环境观测的重要方式，其主浮体系泊于海面以下，搭载各类观测仪器进行观测，观测结束后一般通过释放装置进行回收[1-3]。潜标上浮是潜标回收中的重要过程，分析研究其各组成部分及整个系统在上浮中的速度变化，对潜标回收，特别是深水潜标回收时确定潜标出水时间、出水位置至关重要。回收人员对出水时间和出水位置的准确判断可以帮助搜寻潜标，提高回收效率，同时避免潜标出水时与回收船只发生碰撞，造成损失。

潜标技术是20世纪50年代初首先在美国发展起来的，我国于70年代开始潜标技术的研究[1]。国内外针对不同海流剖面荷载下，锚系潜标的姿态开展了诸多研究[3-6]，这些研究的核心是分析锚系时潜标的受力状况。而针对回收过程中潜标上浮运动，国内外研究并不多见。相关研究集中于观测仪器在海水中运动特征，这一问题的关键是计算仪器受到的海水阻力。阻力的大小可以通过实验、工程流体力学经验公式以及成熟的CFD(计算流体动力学)软件模拟得到。韩光和陶建华[7]将一种新型探头的总阻力分离为摩擦阻力和形状阻力之和，摩擦阻力因数由相对平板的概念求出。黄银水和陶建华[8]通过实验，得到抛弃式温盐探头总阻力因数与雷诺数之间的关系。肖鸿等[9]通过数值模拟，分析探头总阻力因数随雷诺数变化规律。龚德俊等[10]应用有限元软件ANASYS计算了自动返回式采水器总阻力因数。Moonesun等[11]通过4种经验公式、CFD模拟研究潜艇模型阻力，将经验公式、CFD结果与实验进行比较，分析不同计算方法之间的误差，验证了不同经验公式的准确性。

本文以2014年南海北部陆坡M站春、秋两季底流观测潜标回收为实例，根据上浮过程中潜标垂直方向力学分析，建立垂直运动数学模型。最后通过模型与观测结果的对比和验证，分析潜标垂直运动特征。

1南海北部地理环境和观测潜标介绍

南海海底地形复杂，既有宽广的大陆架，又有陡峭的大陆坡，还有宽阔的深海盆地和狭窄的海沟、海槽。海底地势西北高、中部和东南低，平均水深1 212 m[12]。南海北部地理位置及海底地形见图1 。

图1　南海北部地理位置及海底地形Fig.1　Geographical location and seafloor topography of the Northern South China Sea

国家海洋局第一海洋研究所于2013-2014年在南海北部陆坡M站(图1)利用底流观测潜标进行了持续一年的观测，测站水深1 091 m。简化的底流观测潜标结构如图2所示。除去底部重力锚与抓地锚等，回收部分通过Kevlar缆绳以及软硬连接组成一个总长48 m的整体，全部仪器采用串联连接方式。主浮球上搭载了一台AAE信标机。回收时工程船可以通过超短基线(USBL)对主浮球进行水下声学定位。实际回收中，工程船共两次采用高精度超短基线对主浮球位置进行了观测。第一次为2014-05-18春季回收，第二次为2014-09-24秋季回收。本文先以春季回收为例，分析潜标上浮过程中垂直运动。

图2　简化的底流观测潜标结构Fig.2　The simplified structure of the mooring for bottom current observation

2基本假设

南海北部海水水平运动显著(水平流速量级约10-1m/s)，而垂直运动很弱。潜标各部件浮力、阻力性质各异，其水平、垂直相对位置在上浮中可能发生变化。实际上浮过程是复杂的，需要做出合理的假设以简化问题分析。

2.1　忽略水平海流影响假设

潜标上浮中时刻受到水平海流的影响，但水平海流对垂直运动的影响可以忽略。潜标各部件与海流之间的相对速度极大地影响其受到的海水阻力。各部件的垂直上浮速度(量级约100m/s)相对于水平海流流速大得多，各部件水平相对速度远小于垂直相对速度，因此各部件受到的海水阻力主要来自于垂直方向。受到水平海流作用和连接缆绳约束，潜标某些部件会出现姿态偏斜，而姿态偏斜会造成垂直阻力改变。在48 m垂直尺度上，水平海流的垂向差异不大，姿态偏斜有限，并且因姿态偏斜导致的阻力变化相对阻力本身为小量。综上所述，可以忽略水平海流对垂直运动的影响。

2.2　刚性连接假设

潜标依靠Kevlar缆绳、软硬连接等连接为一个系统，逐个分析各个部件的运动比较复杂。可以依据不同部件运动的一致性，将潜标分为如图2所示的4个近似刚性连接部分：主浮球及软硬连接部分能够一致运动，将它们视为刚性连接的整体，记为主浮球部分；2个小浮球、CTD、上部释放器及软硬连接之间由3根并联的Kevlar缆绳连接，形成了“上轻下重”的结构，使得Kevlar缆绳保持绷紧状态，整个结构近似刚性连接，记为中浮球部分；4个小浮球、溶解氧仪、CTD、海流仪、底部释放器及软硬连接之间由3根并联的Kevlar缆绳连接，同样形成了“上轻下重”的结构，也将它们视为一个整体，记为底浮球部分；另外，主浮球与中浮球部分合称为上浮球部分。

2.3　主要部件外形简化假设

潜标主要部件的外形不是完全规则的，这会使绕流阻力的计算变得复杂。考虑到各部件主体接近规则形状，在计算绕流阻力时，针对它们的外形进行简化。简化外形时遵循以下原则：保证简化结果与实际的主体部分在形状上相似，保证简化结果与实际在总面积上一致。经过形状简化，视主浮球、小浮球为球体，CTD、溶解氧仪、海流计、释放器以及Kevlar缆绳为圆柱体。

3潜标垂直运动的分析与建模

3.1　刚性连接部分上浮数值试验

不同刚性连接部分之间依靠柔软缆绳连接，如果底浮球部分速度大于相对位置靠上的中浮球部分或者主浮球部分，那么不同刚性连接部分之间会发生碰撞，可能导致仪器的损坏。并且真实海洋环境中，海水性质随深度会发生变化。要对潜标垂直运动进行分析，首先应了解不同刚性连接部分在不同性质海水中上浮特征。因此设计了上浮数值试验：在整个海域中依次完全充满底层、中层和上层性质的静止海水。当整个海域充满一种性质海水时，将4个刚性连接部分分别自海底释放，考察它们的垂直运动特征。比如，当整个海域中充满底层性质的海水时，各刚性连接部分分别自海底释放的试验就是底层性质海水中上浮试验。

潜标回收时，并未对M站进行温盐剖面观测。陆坡海域的海水温盐在水平方向差异不大，实测温盐可取同一季节距离M站最近的Argo浮标剖面数据。2014-05-03，序列号APEX_SBE_5699的Argo浮标出现在M站东南方向约169.6 km海面，循环周期为170。取该Argo剖面代表M站春季海水温盐状况。秋季的温盐取同一Argo浮标循环周期221的剖面数据。该剖面位于M站东南方向约151.3 km处，出现时间为2014-11-23。

Argo剖面为标准层数据，通过三次函数插值，可以得到表层至水下1 091 m每隔1 m的温盐分布。进一步通过温、盐计算海水的密度和黏性分布。海水密度公式参考UNESCO 1983[13]推荐的计算方案。黏性公式参考Sharqawy等[14]给出的计算方案，但是该结果为1个大气压下海水黏性。考虑海水黏性主要受到温度、盐度影响，直接用1个大气压下的结果代表不同压强下海水的黏性分布。最终获取的M站春秋两季海水的温、盐和密度、黏性垂直分布如图3所示。春秋两季，海水温度(θ)随深度(Z)增加逐渐降低，盐度(S)随深度增加逐渐增大，并在次表层(100~300 m)取得极大值，在中深层(300 m以深)几乎不变。春季混合层深度不到10 m，而秋季能达到60 m。在混合层中，海水密度和黏性变化不大，混合层以下，海水密度(ρ)和黏性(μ)随深度增加较为均匀地增大，不存在密度或黏性的极值。海水的密度和黏性是计算浮力和阻力的关键要素。春季回收中，直接根据深度，取M站春季剖面中1 000,500和100 m深度处海水的密度和黏性代表底层、中层和上层海水的密度和黏性。

图3　M站春、秋两季温、盐和密度、黏性垂直分布Fig.3　The vertical distributions of temperature, salinity, density and viscosity at Station M in spring and autumn

Morrison给出了球体的CD随Re变化的表达式，该式与Schlichting球体绕流实验结果较为一致[16]：

(2)

摩擦阻力因数Cfri取ITTC 1957给出的摩擦阻力公式

(3)

形状阻力因数Cform与摩擦阻力因数Cfri满足一定比例关系：

(4)

绕流阻力因数CT：

(5)

假设某个刚性连接部分由n个部件组成，第i个部件质量为mi，体积为vli，上浮时受到的绕流阻力为Fi(V,υ)。该部分垂直方向受到浮力、重力和阻力，满足：

(7)

(8)

式中，a(t)为t时刻该部分的(垂直)加速度；V(t)为t时刻(垂直)速度；H(t)为t时刻上浮高度。下文讨论的加速度和速度分别指垂直加速度和垂直速度。

初始时刻:

(9)

由式(7)，t时刻的加速度为

(10)

图4　各刚性连接部分在不同性质海水中上浮加速度随时间变化曲线Fig.4　Curves showing the changes of the floating-up acceleration of all parts connected rigidly with time in the seawater with different properties

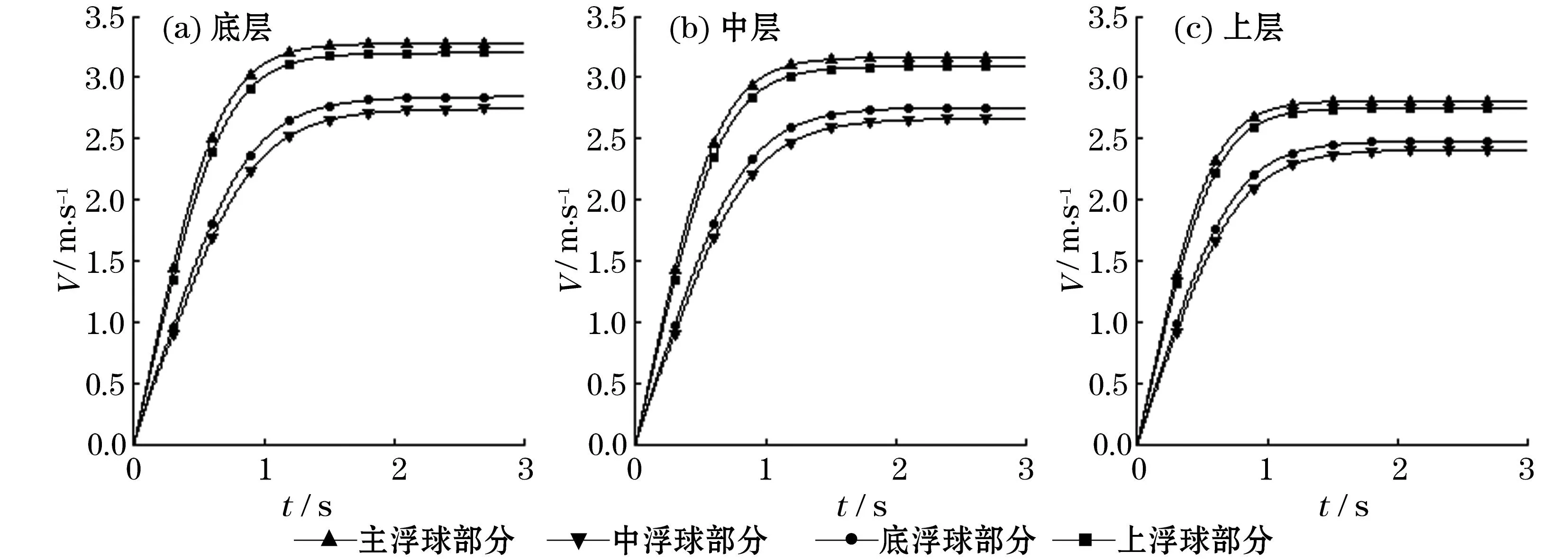
图5　各刚性连接部分在不同性质海水中上浮速度随时间变化曲线Fig.5　Curves showing the changes of the floationg-up acceleration of all parts connected rigidly with time in the seawater with different properties

释放瞬间，各刚性连接部分加速度达到其上浮过程中最大值，然后加速度呈迅速下降趋势，垂直速度相应地迅速增大。在不到2 s的时间内，各部分加速度降至0附近，速度稳定在某一定值。在底、中或上层性质海水中释放后任意时刻，总有主浮球部分的速度大于中、底浮球部分，主、中浮球部分组成的上浮球部分的速度大于底浮球部分。由于各部分几乎处于相同海水环境中，且它们之间依靠柔软缆绳串联，速度最大的主浮球部分必然拉着中浮球部分上浮，两者组成的上浮球部分必然拉着底浮球部分上浮。进一步考虑到海水密度和黏性连续变化，可推断出在春季回收的整个上浮过程中，潜标系统能够保持从上到下，主浮球部分、中浮球部分、底浮球部分的垂直姿态上浮，不存在相对位置靠下的部分速度过快，碰撞到以上部分的可能。

同一刚性连接部分在不同性质海水中速度随时间的变化也是不同的。同一部分在底层性质海水中稳定速度明显要大于中、上层。这一现象是由海水密度、黏性随深度变化导致的，底层海水的密度比中、上层海水的大，但同时底层海水的运动学黏性系数要比中、上层海水的大，受到更大浮力同时也受到更大上浮阻力。稳定速度是重力、浮力与阻力三者平衡结果。

3.2　春季回收中潜标垂直运动模型的建立与求解

上浮数值试验表明，在春季温盐环境下，观测潜标各部件能够保持锚系时的相对位置上浮，不会出现下部部件因速度过大碰撞上部部件的情形。将系统视为刚体，由N个部件组成，锚系状态下第i个部件质心深度为hi。潜标整体受力满足：

(11)

(12)

式中，di为第i个部件在t时刻的质心位置；符号意义同式(7)和式(8)，下标“潜标”表示潜标物理量。初始条件：

(13)

数值计算采用与刚性连接部分上浮试验中一致的算法，同样取步长δt=0.000 1 s。

如图6，春季回收时释放瞬间，加速度达到上浮过程中最大值4.38 m/s2，此后加速度迅速降低，在2.5 s时降至0附近；速度迅速增加，2.5 s时速度为3.12 m/s。定义潜标释放后加速度由最大值迅速减小至0附近，速度迅速增大的阶段为“加速上浮阶段”，而加速度在0附近缓慢变化，速度比较稳定的阶段为“稳定上浮阶段”，该阶段的速度为“稳定上浮速度”。

图7为整个上浮过程中，模型速度随时间变化曲线。模型平均速度约3.0 m/s，上浮共用时349.2 s。稳定上浮速度随时间缓慢降低，2.5 s时速度为3.12 m/s，在海面处降至2.6 m/s。

图6　释放后2.5 s内模型模拟的潜标加速度和速度随时间变化曲线Fig.6　Curves showing the acceleration and the velocity of the mooring simulated by using the model within 2.5 s after release

图7　上浮过程中模型模拟的潜标速度随时间变化曲线Fig.7　The curve showing the changes of mooring velocity simulated by using the model with time in the course of floating-up

4实际观测与模型结果的对比和验证

回收船通过高精度超短基线对主浮球的垂直深度进行观测。该系统由发射基阵、应答器、接收基阵三部分组成，收发器安装在同一探头上，应答器固定于水下拖体[18]。超短基线通过测定声单元的相对差来确定换能器与目标的相对方位角，通过测量声波返回时间来确定换能器与目标距离，再用声速剖面修正波束线，确定声基阵与目标的相对距离，从而确定目标相对位置[18]。影响超短基线定位精度的主要因素有系统自身误差、水体声速剖面变化引起的测距偏差、波浪引起的船体运动、声学基阵安装偏差以及随机误差[18]。回收工程船上安装的超短基线为高精度超短基线，观测误差为5‰。其声学基阵在使用前已进行了安装标定，消除了安装误差；收发器内置姿态传感器，可以校正船体横、纵摇对基阵探头的影响，主要误差来源于随机误差。

释放水深(约1 040 m)至978.27 m之间，由于声波的多路径、声信号强度较弱、声信号干扰等，观测深度出现异常跳动；潜标上浮至海面以下265.98 m时超出了收发基阵接收范围，基阵无法接收到信号而停止读数。最终选取水下978.27~265.98 m，稳定上浮阶段的有效观测。工程船使用的超短基线误差为5‰，考虑每隔1 s输出一个定位位置，水下1 000 m处观测速度误差最大能达到5 m/s，与垂直速度一个量级。这一误差主要为随机误差，通过三次函数拟合观测曲线去除影响。

春季回收中，观测速度曲线、观测速度拟合线与模型速度曲线如图8所示。观测速度随时间振荡变化，起伏过于剧烈，其中包含了较大的观测误差。潜标系统在上浮过程中不可能完全保持刚性整体，周围海水性质变化和海水流动必然造成主浮球与以下连接的部分不断调整姿态和速度来适应周围环境，主浮球实际垂直速度应当是振荡变化的。而是否存在如此大的振幅需进一步考察。拟合速度能去掉随机误差影响，更好地反映真实速度。模型用更少的时间完成水下978.27~265.98 m一段的上浮，模型速度平均为3.0 m/s。而拟合为2.8 m/s，两者相差0.2 m/s。在732 m附近，两者存在相同速度3.1 m/s，732 m以深，拟合速度大于模型，732 m以浅，模型速度大于拟合。潜标在水下978 m附近的拟合速度为4.1 m/s，模型为3.1 m/s，在水下269 m附近的拟合速度为2.0 m/s，模型为2.9 m/s，两者最大相差1 m/s。

秋季回收中，高精度超短基线观测的有效深度为水下988.51~29.57 m。通过上浮数值试验，可推断出在秋季温盐条件下，潜标同样整体上浮的结论。利用上浮模型对秋季回收中潜标上浮过程进行了模拟，观测速度曲线、观测速度拟合线与模型速度曲线如图 9所示。

图8　春季回收中观测速度、观测速度拟合线以及模型速度随时间变化曲线Fig.8　Curves showing the changes of the observed velocity and its fitted values and the model velocity with time during the release in spring

图9　秋季回收中观测速度、观测速度拟合线以及模型速度随时间变化曲线Fig.9 Curves showing the changes of the observed velocity and its fitted values and the model velocity with time during the release in autumn

秋季回收中观测速度随时间同样存在振荡，但是振幅相对于春季要小，观测速度较春季更为稳定。潜标接近海面时，观测速度突然剧烈变化，这是由观测误差造成的。模型用了更少的时间完成了水下988.51~29.57 m一段的上浮。模型速度和拟合速度平均值分别与春季一致。两者在704 m附近存在相同速度3.1 m/s，704 m以深，拟合速度大于模型，704 m以浅，模型速度大于拟合。潜标在水下988 m附近的拟合速度为4.4 m/s，模型为3.1 m/s，在水下30 m附近的拟合速度为1.9 m/s，模型为2.7 m/s，两者最大相差1.3 m/s。

观测与模型都表明，在稳定上浮阶段，稳定速度随时间缓慢下降。这一现象是由潜标上浮过程中，周围海水的密度与黏性随深度变化引起的。主浮球就在变化的海水环境中不断调整速度来维持整体受力平衡。这与刚性连接部分上浮数值试验一致，并且释放水深越大、海水性质垂向差异越大，这一现象越明显。

模型结果与实际观测存在一定的差异，可能原因有：模型使用的温盐为同一季节距离M站最近的Argo剖面数据，该温盐剖面与M站回收时实际情况仍存在一定差异；模型利用温盐数据、通过经验公式得到了1个大气压下的海水黏性，该黏性与实际存在差异；做出的水平海流不影响垂直运动的假设过于理想。在某些水平海流垂向差异大、流速大的水层，水平海流对潜标不同部件造成的姿态偏斜比较显著，进一步引起绕流阻力的变化，影响潜标垂直运动；潜标主要部件的外形经过了简化，计算的绕流阻力与实际存在差异。

综上所述，上浮过程中，模型结果虽然与实际观测存在差异，但是差异并不显著，模型曲线与观测拟合线比较接近，建立的模型能比较准确地模拟实际垂直上浮过程。

5结论

以2014年南海北部陆坡M站春、秋两季底流观测潜标回收为实例，建立垂直运动数学模型，通过模型与观测结果的对比和验证，研究潜标上浮过程中的垂直运动特征。潜标上浮过程可以分为加速上浮阶段和稳定上浮阶段。释放后，潜标即进入加速上浮阶段。该阶段特征为：潜标的加速度由释放瞬间的最大值迅速降低至0附近，速度则由释放时的0，迅速增大至稳定值。经历完加速上浮阶段，潜标即进入稳定上浮阶段，直至浮出海面。稳定上浮阶段特征为：加速度在0附近缓慢变化，速度相对稳定，加速度和速度存在一定变化，但幅度有限、过程缓慢。该阶段的另一个特征是上浮速度随时间缓慢减小。这是潜标调整速度适应海水密度和黏性垂直变化的结果。模型与观测的对比表明，模型速度曲线和观测速度拟合曲线比较接近，平均模型速度与平均观测速度仅相差0.2 m/s。模型能够反映出稳定速度随时间缓慢下降的特征。

影响潜标上浮过程中垂直速度的因素有：潜标整体配置情况；释放海域海水的密度、黏性等性质；释放海域海水运动情况；潜标各部件在水下不同海流荷载下的阻力情况。由于潜标并非刚体一块，不同部件之间相互作用而上浮，速度是振荡变化的。本文建立的上浮模型仍存在诸多待改进之处：模型需要更准确的释放海域海水密度和黏性垂直分布。水平海流会引起仪器姿态偏斜而影响垂直阻力，阻力变化应当考虑进去。本文对主要部件的外形做出简化，基于工程流体力学中的经验公式计算阻力，结果与真实情况仍然存在差异。需进一步通过实验或CFD软件模拟，获取更接近实际的阻力大小。

潜标垂直运动模型可用来指导实际工程中潜标或其他水下物体上浮的问题分析，对水下仪器的回收工作有一定参考意义。

参考文献：

[1]毛祖松.海洋潜标技术的应用与发展[J].海洋测绘,2001,(4):57-58.

[2]孙仲汉.关于发展我国漂流浮标和锚泊浮标技术的建议[J].海洋技术,2000,19(2):13-17.

[3]李飞权，张选明，张鹏，等.海洋潜标系统的设计和应用[J].海洋技术,2004,23(1):17-21.

[4]NATH J H, FELIX M P. Dynamics of single point mooring in deep water[J]. Journal of the Waterways, Harbors and Coastal Engineering Division,1970, 96(4): 815-833.

[5]王明午.海洋潜标系统的静力分析和姿态计算[J].海洋技术,2001,20(4):39-47.

[6]兰志刚，杨圣和，刘立维，等.深海剖面测流潜标系统设计及姿态分析[J].Marine Sciences,2008,32(8):21-24.

[7]韩光，陶建华.新型航空海水温度,盐度,深度探头运动特性的计算方法和实验验证[J].水动力学研究与进展:A辑,2001,16(4): 467-471.

[8]黄银水，陶建华.线圈释放式温、盐、深探头运动特性的数值计算方法研究[J].海洋技术，2003,22(1):45-48.

[9]肖鸿，刘长根，陶建华.抛弃式温盐探头阻力系数的数值模拟及其实验验证[J].海洋技术，2006,25(1):35-37.

[10]龚德俊，于建清，张澎湃. 自动返回式采水器的阻力系数计算与方法验证[J].海洋科学，2008, 32(8): 16-20.

[11]MOONESUN M, JAVADI M, CHARMDOOZ P, et al. Evaluation of submarine model test in towing tank and comparison with CFD and experimental formulas for fully submerged resistance[J]. Indian Journal of Geo-Marine Sciences, 2013, 42(8): 1049-1056.

[12]孙湘平. 中国近海区域海洋[M].北京: 海洋出版社, 2006.

[13]FOFONOFF N P, MILLARD R C. Algorithms for computation of fundamental properties of seawater[J].Unesco Technical Papers in Marine Science, 1983, 44:1-53.

[14]SHARQAWY M H, LIENHARD J H, ZUBAIR S M. Thermophysical properties of seawater: a review of existing correlations and data[J].Desalination and Water Treatment, 2010, 16(1-3): 354-380.

[15]陈卓如，金朝铭，王洪杰，等.工程流体力学(第2版)[M].北京:高等教育出版社,2004.

[16]MORRISON F A. An introduction to fluid mechanics[M].New York: Cambridge University Press, 2013.

[17]BERTRAM V. Practical ship hydrodynamics[M].Oxford: Elsevier, 2012.

[18]王德刚，韩富江，来向华，等. 超短基线定位原理及校正方法研究[J].海洋科学,2011,35(2): 77-81.

Mathematical Modeling and Result Validation of

Mooring Vertical Movement in the Course of Floating-up

GUO Yong-qing1, LI Xiao-long2, XIONG Xue-jun1,3

(1.TheFirstInstituteofOceanography,SOA, Qingdao 266061, China;

2.CNOOCDeepwaterExploitationCo.Ltd., Shenzhen 518067, China;

3.KeyLabofMarineScienceandNumericalModeling,SOA, Qingdao 266061, China)

Abstract:Taking the recovering of the Bottom Current Observation Mooring, which was carried out at Station M on continental slope of the Northern South China Sea in spring and autumn of 2014, as the example, the vertical movement characteristics of the mooring in the course of its floating-up are analyzed by means of mathematical modeling. Firstly, it is assumed that the influence of horizontal current is neglected, the mooring system is connected rigidly and the shape of the mooring's major parts is simplified. From the numerical experiments made for floating-up of the rigidly connected parts of the mooring, it is concluded that after releasing all the parts of the mooring can keep their relative position unchanged and float upward as a whole. Thus, the vertical movement model is established by regarding the mooring system as a rigid body. Two times of mooring recovery are simulated by using the model and comparisons are made between the results from the model and from the observations with high-precision USBL. The results indicate that the overall course of the mooring floating-up can be divided into two stages: the accelerated floating-up stage and the stable floating-up stage. The velocity curve given by the model is close to the fitted curve of observed velocity. The differences between the mean velocity given by the model and the observed mean velocity are 0.2 m/s. The model can reflect that in the stable floating-up stage the floating-up velocity decreases slowly with time. The floating-up vertical velocity of all parts of the mooring shows an oscillating change. The Model can provide a quantitative reference for the recovering of relevant underwater instruments.

Key words:mooring recovery; vertical movement of the mooring; mathematical modeling; numerical computation; high-precision USBL

中图分类号：P731.2，P71

文献标识码：A

通讯作者，熊学军(1976-)，男，研究员，博士，主要从事区域海洋动力学及调查技术方面研究. E-mail:xiongxj@fio.org.cn(杜素兰编辑)

作者简介：郭永青(1990-)，男，硕士研究生，主要从事区域海洋动力学及调查技术方面研究. E-mail: aiiky@163.com*

收稿日期：资助项目：国家科技重大专项子任务——南海陆坡底流观测(8400531981)；工业和信息化部海洋工程装备科研项目——500米水深油田生产装备TLP自主研发；国家自然科学基金——黄海暖流的多时相特征及其发生机制研究(41376038)；海洋公益性行业科研专项——常用海底声纳测量仪器计量检测关键技术研究与示范应用(201305034)

文章编号：1002-3682(2015)02-0011-13