基于格子Boltzmann法物体绕流模拟与解析
2015-12-21马明远王勇西南石油大学四川成都610500
马明远 王勇(西南石油大学,四川 成都 610500)
格子Boltzmann方法是近20年来迅速发展起来的一种介观模拟方法,以其自身拥有的物理意义清晰、边界处理简单、程序简单、并行性好等特点而受到人们的关注[1]。本文使用D2Q9单松弛模型进行了Poiseulle流模拟以验证模型的准确性,并使用该模型模拟物体绕流,体现了出格子Boltzmann方法的实际应用价值。
1 绕流的格子Boltzmann模型
与传统计算流体力学方法不同,格子Boltzmann方法的出发点并不是基于连续流体的Navier-Stokes方程,而是基于气体动理论的基本方程--Boltzmann方程。一个完整的格子Boltzmann模型通常包含以下三要素[2]:速度离散模型、平衡态分布函数、分布函数的演化方程。
1.1 速度离散模型
在本文中我们采用钱跃竑等人提出的D2Q9模型[3],D2Q9模型中的粒子迁移路径如图1所示。
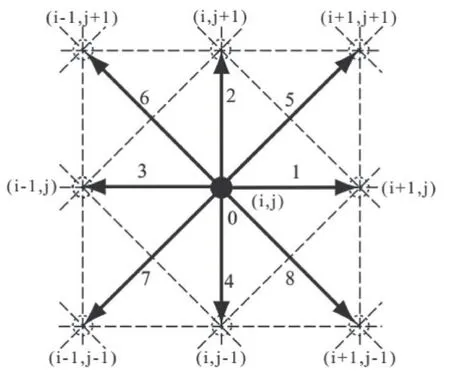
图1 D2Q9模型
其中,粒子存在于节点处并只能按照图1所示连线方向运动,因此,在某一节点处只可能存在以下三种粒子:

我们采用常规的正方形网格,有δx=δt、c=δx/δt,其中δx和δt分别为网格步长和时间步长。
1.2 平衡态分布函数
D2Q9模型所采用的平衡态分布函数形式如下:
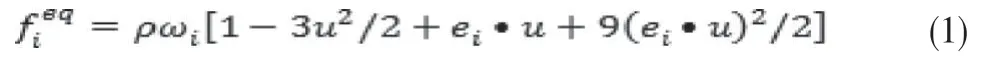
这里,
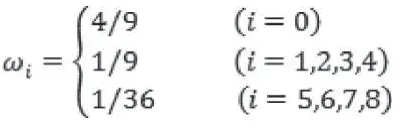
模型的宏观密度和宏观速度可由下式求得:

1.3 分布函数的演化方程
格子Boltzmann法假想粒子具有迁移和碰撞两个过程,在迁移时,粒子根据速度方向迁移至相邻的格子节点,这时有分布函数:

碰撞时:
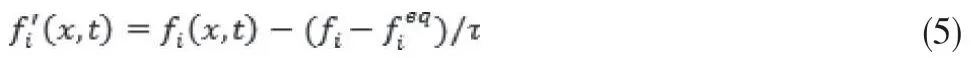
这里的τ为无量纲弛豫时间,由流体从非平衡态分布往平衡态分布趋近的速度决定。
1.4 边界处理格式
对于静止的固体边界,无法使用式(4)和(5)求得边界处的分布函数,在这种情况下我们使用bounce-back边界[4],即对边界上的粒子做180°的弹回处理。这里,以下边界为例便有使用bounce-back边界处理格式能够严格的保证系统的质量和动量守恒且操作简单。
对于入口和出口,使用周期性边界处理格式,即是指当流体粒子从一侧边界离开流场时,在下一个时步便会从另一侧的流场边界进入,因此该边界处理格式同样可以严格的保证整个系统的质量和动量守恒[5]。周期性边界条件处理格式可以表示为
2 数值试验
在这里我们对一个150*30区域作为对象进行计算模拟,在上下边界处采用bounce-back边界处理条件,对左右流入流出边界采用周期性边界条件,给定全体格点沿方向有初始流动速度,以及雷诺数。首先我们通过D2Q9模型模拟二维Poiseulle流动,从图2中我们可以清楚地看到该模型的流速分布与Poi⁃seulle流理论解的流速分布高度一致,D2Q9模型的准确性因此得到了很好的验证。
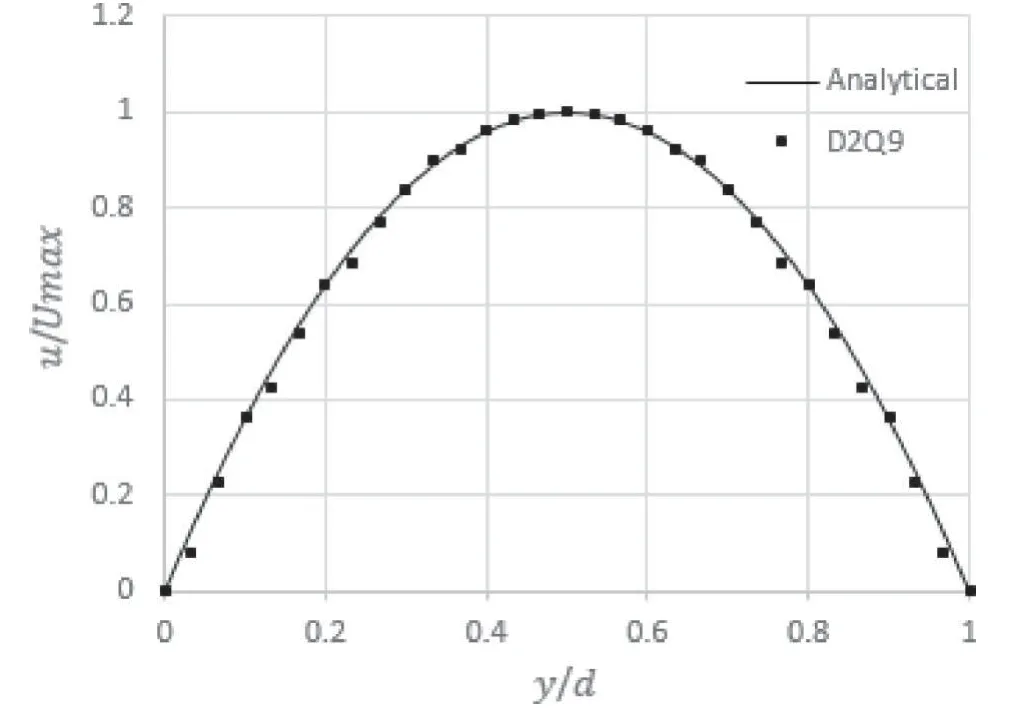
图2 Poiseulle流流速分布
此时在其中放置一个半径为5的二维圆柱,并在该物体边界采用bounce-back边界处理格式。于是我们便可以得到如图3和图4所示和方向上的无因次流速分布。
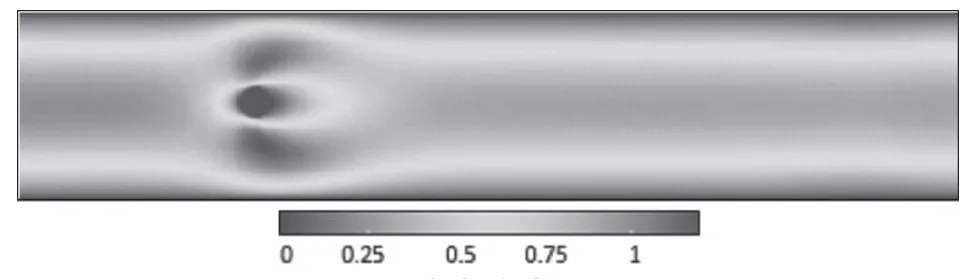
图3 方向流速
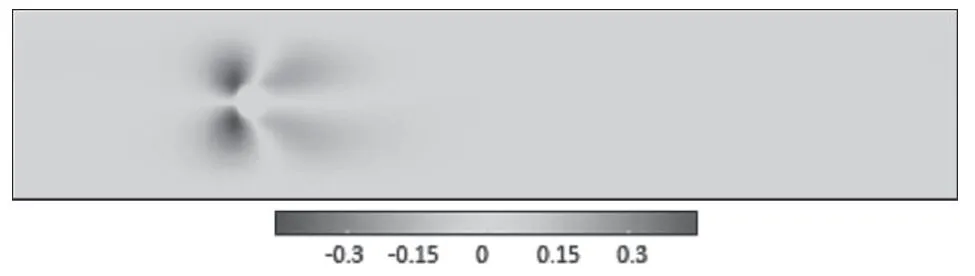
图4 方向流速
3 结语
本文通过二维Poiseulle流验证了格子Boltzmann方法D2Q9单松弛模型的模拟精度,并且使用该方法实现了二维绕流的再现,说明了格子Boltzmann方法是一种解决模拟流动问题的有效手段,拥有应用到实际工程研究中的价值。
[1]Chen S,Doolen G D.Lattice Boltzmann method for fluid flows.Annual Review of Fluid Mechanics,1998.
[2]Wolf-Gladrow D A.Lattice-gas Cellular Automata and Lat⁃tice Boltzmann Models:An Introduction.New York:Springer,1992.
[3]Qian Y H,d’Humières D,Lallemand P.Lattice BGK mod⁃els for Navier-Stokes eq-uation.Europhysics Letters,1992.
[4]Lacallee P,Boon J,Noullez A.Boundaries in Lattice Gas Flows.Physica D,1991.
[5]何雅玲,王勇,李庆.格子Boltzmann方法的理论及与应用.北京:科学出版社,2009.
