基于时频图像处理的多分量LFM信号分离
2015-12-21张国毅胡鑫磊王晓峰
刘 歌,张国毅,胡鑫磊,王晓峰
(1.空军航空大学信息对抗系,吉林 长春130022;2.海军航空工程学院,山东 烟台264001)
0 引言
由于电磁环境日益复杂,在雷达侦察系统中,宽带接收机经常会截获到多个辐射源信号。这些辐射源信号会在时域上发生交叠,从而形成了多分量信号[1]。而在实际侦察中,LFM 信号应用非常广泛,在复杂密集的信号环境中对多分量LFM 信号进行有效分析具有重要的实际意义。要对多分量LFM 信号中的各个分量进行有效的参数估计,必须首先实现信号分离。随着时频分析方法研究的不断深入,近年来将图像处理技术与时频分析相结合的方法也逐渐发展起来。文献[2]运用图像处理的技术对多分量辐射源信号的时频图进行处理,但仅限于图像质量的改善,而且在低信噪比的情况下不适用;文献[3]也采用图像处理的技术处理时频图像,得到信号的瞬时频率,但是无法进行后续其他参数的估计;文献[4]能对多分量雷达辐射源信号进行有效的检测与分离,但只针对时频域不交叠的多分量信号。
针对以上问题,本文从图像处理的角度提出一种分离方法,首先对多分量LFM 信号SPWVD 进行Radon变换,得到各分量的调频斜率的估计值。同时,将SPWVD 时频图转化成二值图像,利用调频斜率估计值计算得到的直线倾斜角对二值图像进行形态学处理,达到多分量LFM 信号的粗分离,最后采用连通区域标记法实现信号分量细分离。仿真实验表明,该方法具有很好的抗噪性能。
1 多分量LFM 信号模型
设接收到的多分量LFM 信号为s(t):
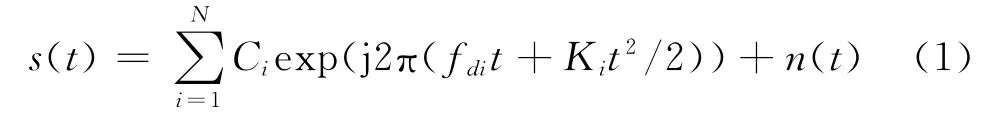
式中,N 为LFM 分量的个数,Ci为第i个LFM 分量的幅度(本文均设为1),fdi为各分量的起始频率,Ki为调频斜率,n(t)为加性白噪声。
2 多分量LFM 信号时频分析
对信号s(t)进行Wigner-Ville分布(WVD)[5]:
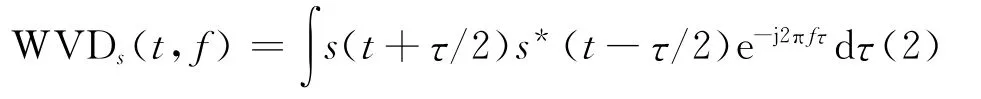
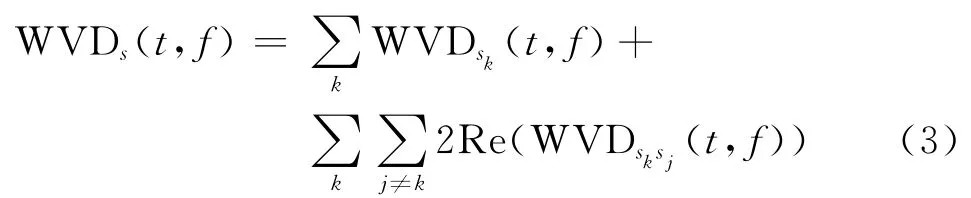
式中,WVDs(t,f)表示第k个信号分量和第j个信号分量之间的互WVD,即交叉项。
因此,当对多分量信号进行WVD 时,会在多分量信号间产生互时频分布即交叉项,成为图像上的虚假信号,从而给信号的时频分析造成困扰。对于任何一个多分量信号,二次型时频分布都会产生交叉项。
为了抑制WVD 产生的交叉项,本文采用的时频分析方法是SPWVD,可以表示为:
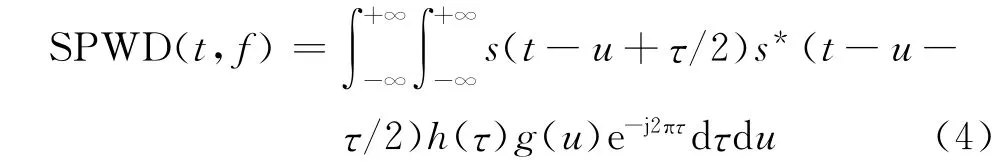
式中,h(τ)和g(u)为窗函数。
3 时频图像处理原理
当采用灰度图像的方式对信号的时频分析结果进行表示时,图像中的像素点的不同灰度表示对应时频点的幅度值。时频平面上信号的自项可以看作是图像中的“对象”,而加性噪声与时频分布中的交叉项则构成了图像的“背景”。因此,对多分量LFM 信号的时频图进行处理就相当于在灰度图像中去除背景而保留对象的过程。
本文先将时频图像转化为灰度图,然后采用自适应滤波的方法来初步滤除噪声的影响,接着将灰度图转化为二值图像,为信号的分离作准备。
3.1 自适应滤波和二值化
在多分量LFM 信号时频图像上,噪声表现为具有较高频率的灰度变化,主要对应灰度值较低的高频成分。而信号的自分量由于内部自相关性和时域窗口运算带来的SNR 的改善作用,其主要表现为灰度值较高、幅度恒定的低频成分。因此,可以采用自适应维纳滤波器[6]来初步滤除噪声在时频图像上对LFM 信号自分量的影响,这是因为维纳滤波器对高斯白噪声的抑制效果最好。
为了减少后期图像处理的计算量和存储空间,将滤波后的灰度图像转化为仍然可以反映图像整体和局部特征二值图像,即图像的二值化,也就是我们平时所说的阈值化分割。
设阈值处理后得到的二值图像为Bs(t,f),则有:
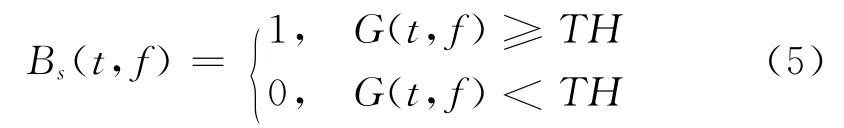
式中,TH 为设定的阈值,G(t,f)为经自适应维纳滤波后的时频灰度图像。
因此,确定合适的阈值是分割的关键,阈值选择过大会去除图像中的对象,选择过小会达不到有效去除噪声的目的。本文的阈值选取采用的是一维最大熵法。
3.2 时频图像形态学处理
时频图像进行二值化后,多分量LFM 信号被进一步展宽,因此本文采用数学形态学[7]方法对信号分量进行粗分离和细化。数学形态学是以形态结构元素为基础对图像进行分析的数学工具。基本思想是用一定形态的结构元素去度量和提取图像中的对应形状以达到对图像识别和分割的目的。形态学的基本操作是对集合进行腐蚀和膨胀。
设A 为结构元素,对二值图像Bs(t,f)进行腐蚀运算,可以表示为:
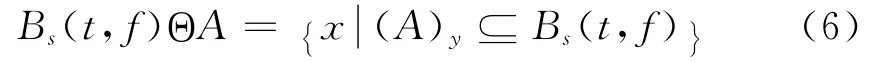
式中,y 是表示Bs(t,f)平移的位移量,Θ 表示腐蚀运算的运算符。
对二值图像Bs(t,f)进行膨胀运算,可以表示为:
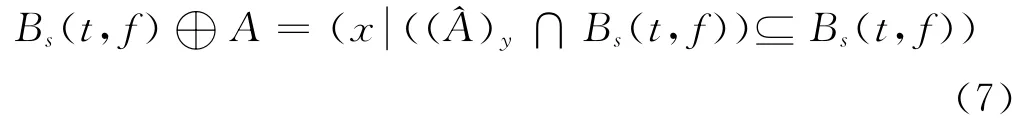
式中,y 表示Bs(t,f)平移的位移量,⊕表示膨胀运算的运算符,^A 为结构元素A 关于原点的反射集合。
以上公式可以看出,形态算子的实质是表达物体或形状的集合与结构元素间的相互作用,结构元素的形状就决定了这种运算所提取的信号的形状信息。在形态学中,结构元素是最重要最基本的概念[8]。结构元素的形状不同,腐蚀与膨胀运算的结果就不同。一般文献在选用结构元素时经常不考虑被处理的对象的形状与结构元素之间的关系,从而导致腐蚀或膨胀的结果不尽如人意。
本文充分利用线性结构元素与LFM 信号相匹配的特点,选取具有一定角度的直线段作为腐蚀与膨胀运算的结构元素,从而达到将多个LFM 信号粗分离的效果。在本文算法中结构元素角度的设定与LFM的倾斜角有关。
形态学骨架化可以把二值图像区域缩成很细的线条,以逼近区域的中心线,达到减少图像冗余成分,只留下时频图像最基本信息的目的。
由于SPWVD的核函数的平滑作用以及时频图像二值化,导致信号的自分量被展宽。本文通过对腐蚀膨胀之后的二值图像骨架化,提高信号的时频聚集性。
设腐蚀与膨胀后的图像为Cs(t,f),则对其骨架化可以表示为:
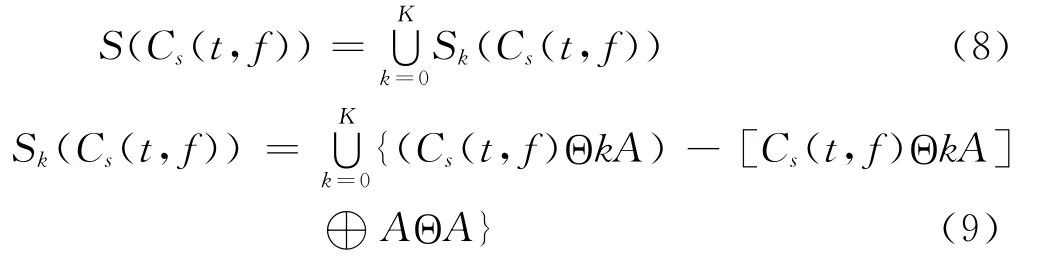
式中,Sk(Cs(t,f))为骨骼子集,Cs(t,f)ΘkA 表示对Cs(t,f)连续腐蚀k次,A 为结构元素。
时频图像骨架化后可能会出现许多毛刺,对此可以采用去毛刺[7]算法,将得到的时频脊线上的毛刺去除掉,达到平滑的目的。
3.3 连通区域标记法
经过形态学处理后的图像中仍残留着其他信号分量的信息以及少量的噪声,采用连通区域标记法[7]实现信号分量的细分离。
二值图像的连通区域标记是从仅由“0”像素(通常表示背景点)和“1”像素(通常表示前景点)组成的一幅点阵图像中,将相互邻接(4-邻域或8-邻域)的“1”值像素集合提取出来。其目的就是要寻找图像中所有的目标对象,并且将属于同一目标对象的所有像素用唯一的标记值进行标记。本文选用的是8-邻域的连通,对图像上的信号分量以及冗余信息进行标记,根据不同连通区域的标号不同将信号分量提取出来。
3.4 多分量LFM 信号分离和参数估计的流程
本文方法的处理流程如图1所示。
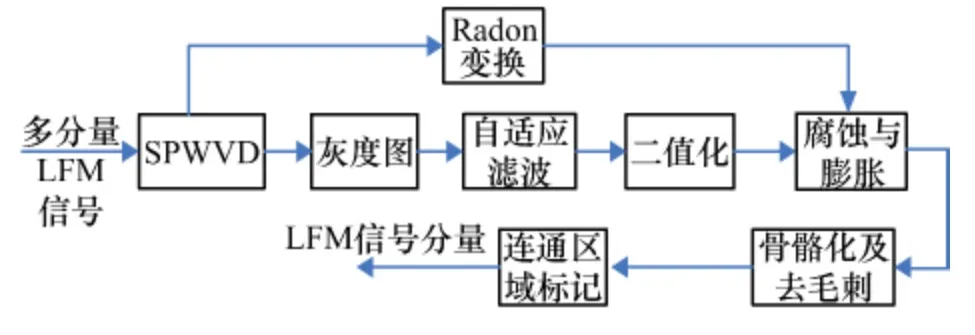
图1 本文方法处理流程
4 仿真分析
4.1 仿真实验
为了验证本文方法的有效性,采用时频交叠的三分量LFM 信号进行仿真分析,对同一多分量LFM 信号在不同信噪比下进行分离。各分量的参数设置如表1所示。
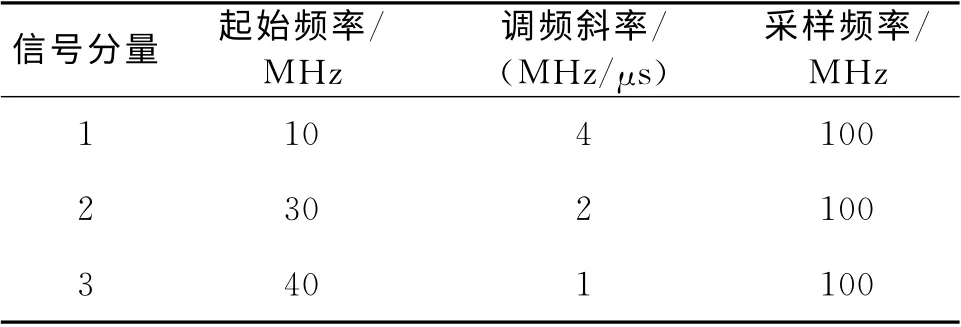
表1 各分量的参数设置
当信噪比为5dB时,三分量LFM 信号的时频分布如图2所示。由于核函数的平滑作用,进行SPWVD变换之后,信号自分量被展宽了。该信号分离的结果如图3所示。经过本文算法处理之后,LFM 信号各分量被很好地分离开来,且信号的时频聚集性增强。
当信噪比为0dB 时,三分量LFM 信号的时频分布如图4所示。该信号分离的结果如图5所示。在图5(c)中可以看到信号出现了断裂,但整体来看,并不影响信号分离的效果以及后续的参数估计。
当信噪比为-7dB 时,三分量LFM 信号的时频分布如图6所示。该信号分离的结果如图7所示。信号各分量出现了不同程度的断裂以及丢失。这是由于信号受到噪声的干扰严重,从而影响处理结果。经过大量的仿真实验证明,本文算法在信噪比大于-6dB的情况下有效。
4.2 性能分析
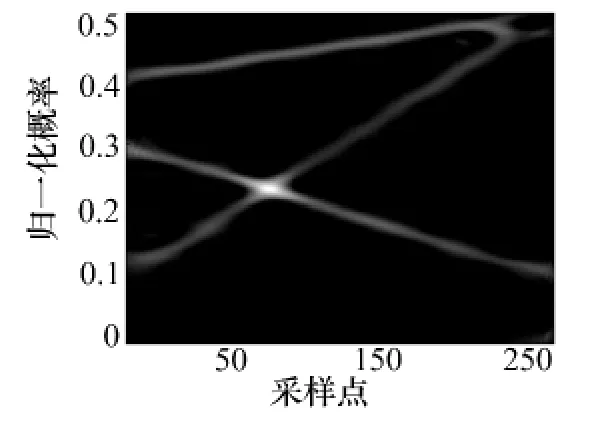
图2 三分量LFM 信号的 SPWVD,SNR=5dB
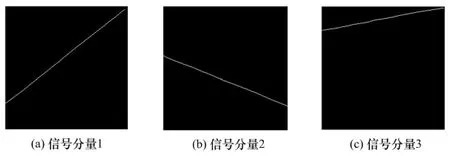
图3 三分量LFM 信号的分离结果(二值图表示),SNR=5dB
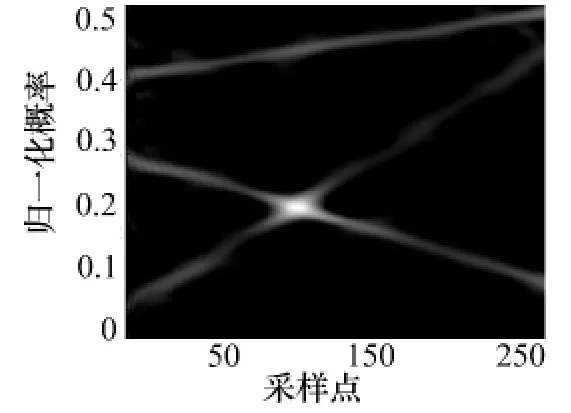
图4 三分量LFM 信号的 SPWVD,SNR=0dB
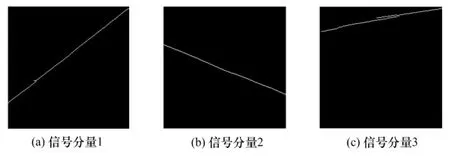
图5 三分量LFM 信号的分离结果(二值图表示),SNR=0dB
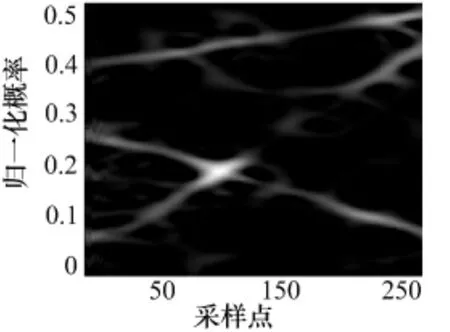
图6 三分量LFM 信号的SPWVD,SNR=-7dB

图7 三分量LFM 信号的分离结果(二值图表示),SNR=-7dB
图8表明,随着信噪比的增大,相关系数逐渐变大,分离提取的信号分量与初始信号分量的相似程度越来越高,从而说明分离效果越来越好。仿真结果表明,本文算法在0dB 时,分离相关系数达到0.93 以上,具有较好的抗噪性。在信噪比小于2dB 的情况下,信号分量1的相关系数比其他两个分量的相关系数大,这是因为信号分量1与其他两个分量没有交叠的部分,这也可以说明本文算法在分离时频不交叠多分量LFM 信号时也适用,且效果会更好。
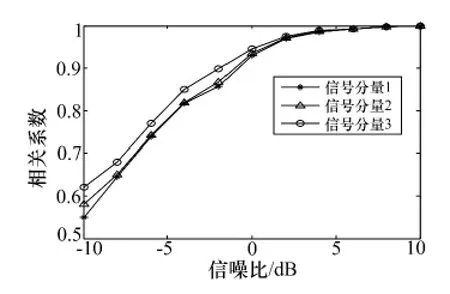
图8 多分量LFM 信号分离性能分析曲线
5 结束语
本文提出了一种将时频分析和图像处理相结合的多分量LFM 信号分离方法,将时频分布转化为二值图像后,采用图像处理中的形态学方法进行信号的粗分离,然后利用连通区域标记的方法进行细分离。实验结果表明该方法在较低信噪比条件下能够获得较好的分离效果,为时频交叠的多分量LFM 信号的分离提供了一种可行方案,为下一步对该种信号进行参数估计提供了重要的参考价值。■
[1]荣海娜,张葛祥,金炜东.多分量雷达辐射源信号检测新方法[J].系 统 工 程 与 电 子 技 术,2009,31(9):2096-2100.
[2]邹兴文,张葛祥.基于图像处理技术的雷达辐射源信号时频特性分析[J].电路与系 统学报,2009,14(3):135-140.
[3]白航,李传兵,李富军,等.基于时频图像形态学的雷达信号IF估计[J].航天电子对抗,2013,29(2):57-60.
[4]刘勇,张国毅,齐兴龙,等.多分量雷达辐射源信号的检测与分离[J].航天电子对抗,2014,30(3):37-41.
[5]张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998.
[6]Gonzalez RC,Woods RE,Eddins SL.Digital Image Pro-cessing Using MATLAB[M].2nd ed.Gatemark Publishing,lnc.,2009.
[7]Gonzalez RC,Woods RE.Digital Image Processing[M].2nd ed.Publishing House of Electronics Industry,Beijing,2002.
[8]唐晓强,赖惠成.形态学结构元素选取算法的研究[J].通信技术,2010,43(7):161-162.
