分离式垂直方向充退磁线圈数值仿真研究

彭毓川，孟立飞，肖 琦，张绍华，刘超波

（北京卫星环境工程研究所，北京 100094）

0 引言

航天器在轨运行时，其磁矩同地球磁场相互作用会产生干扰力矩，影响航天器的姿态，使航天器自旋速率下降，并造成自旋轴的长期漂移[1]，增大航天器的控制难度。因此在航天器上天之前，必须对其进行磁性能检测，并采取一定的磁矩控制措施。充磁和退磁试验是航天器磁性能检测的重要手段[2]。

目前国际上各主要磁试验设备中，美国NASA戈达德空间飞行中心（GSFC）磁试验设备的充退磁线圈为圆形亥姆霍兹线圈形式，其直径2.9 m，2 个线圈分别装在支撑小车上，间距可调节；德国工业设备管理公司（IABG）磁试验设备的充退磁线圈为方形亥姆霍兹线圈形式，其边长3.7 m，2 个

线圈分别装在支撑小车上，间距可调节；日本JAXA 磁试验设备的充退磁线圈为螺旋管形式，外边有2 对用于抵消垂直方向和水平方向地磁场分量的方形线圈，螺旋管线圈直径2 m、高2 m[3]。

北京卫星环境工程研究所的CM2 整星磁试验室具备1 套方位固定的水平向充退磁设备，可由承载卫星的无磁转台水平向旋转90°，完成水平2 个方向的充退磁试验；由于卫星在垂直方向上无法翻转，故用另外的由2 组半圆形线圈围绕卫星对接而成的充退磁线圈产生垂直方向磁场，每组半圆形线圈重约490 kg。在每次垂直向充退磁试验前，均需要4 名工作人员在设备的4 个接插处同时以大致相同的速率操作力矩机构实现电连接器的接插，工序较烦琐，且对试验人员的操作准确性要求较高。显然，简便快捷的垂直方向充退磁系统更加符合当前试验任务的需要。

本文在简要分析现有充退磁线圈设备的结构和充退磁原理的基础上，提出一种安装简便的分离式垂直方向充退磁线圈结构。并利用仿真平台对该结构进行了各项磁场均匀性分析以及与原设备的误差分析，以验证线圈结构的正确性，保证其在原理及性能上均与原设备保持一致。

1 分离式垂直方向充退磁线圈结构的提出

CM2 试验室现有的垂直方向充退磁线圈结构如图1所示。

图1 CM2 垂直方向充退磁线圈结构Fig.1 The structure of the vertical magnetization-demagnetization coil of CM2 with a couple of connectors

由电磁学理论可知，

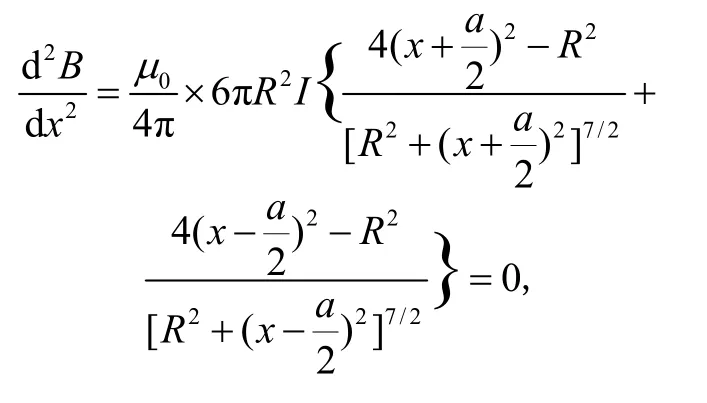
式中：B为两线圈在轴向场点的磁场叠加；x为场点的轴向坐标；µ0为真空磁导率；R为线圈半径；a为两线圈轴向距离；Ⅰ为流过的稳恒电流。当a=R时，d2B/dx2= 0。因此，对于如图1(b)所示的亥姆霍兹线圈，当两线圈电流强度相等，回绕方向一致，且轴向距离与线圈半径相等时，可在线圈中心区域产生适合于退磁试验的均匀轴向磁场[5]。

下面取单个线圈进行分析，如图2所示。

图2 单个线圈轴向磁感应强度分析Fig.2 Analysis of the axial magnetic field of a single coil

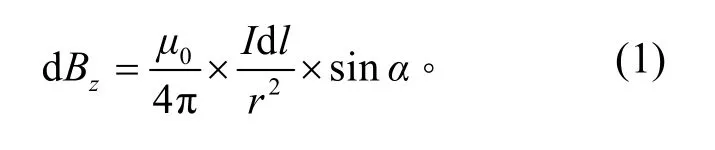
根据式(1)及图2，单个线圈轴线上任一点的磁感应强度为

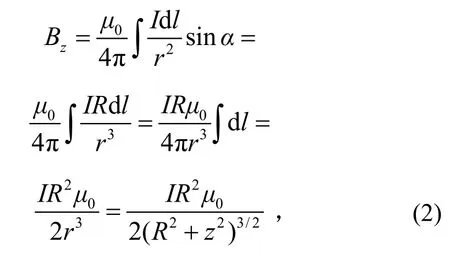
其中z为该点到线圈圆心的距离。

毕奥-萨伐定律描述的是闭合回路产生的总磁场，本文的研究将线圈由接插处分开为2 个半圆线圈，分别向两边平移距离d，将每个半圆线圈看作某个闭合载流回路的一部分，单独分析其在原完整线圈轴线上某点的磁感应强度，如图3所示。

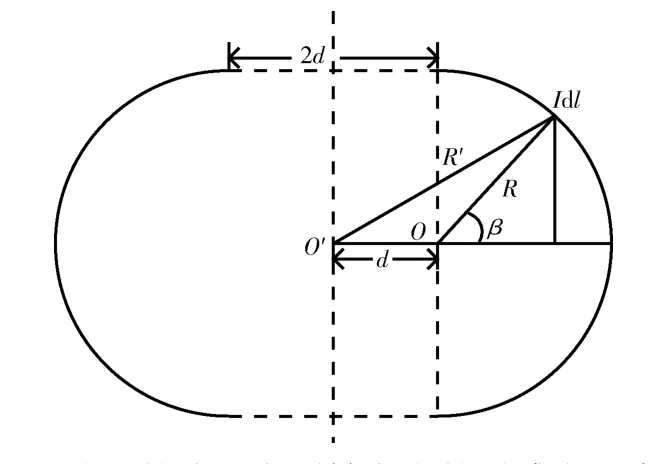
图3 平移后的线圈在原轴向上的磁感应强度分析Fig.3 Analysis of the axial direction magnetic field of the disconnected coil

由图3可知，

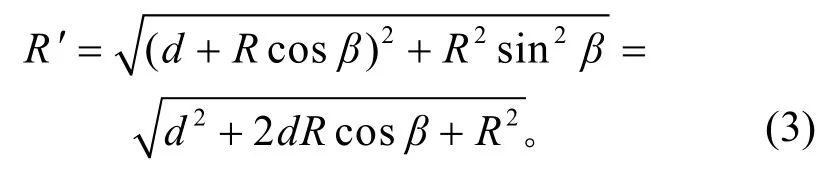
再结合图2可知，

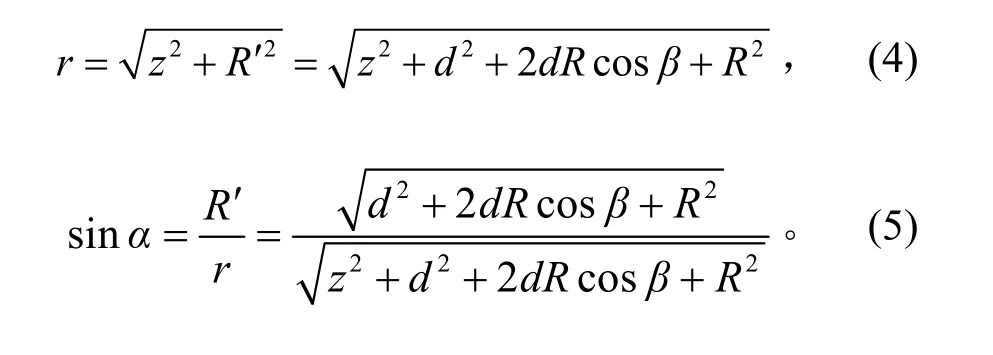
根据弧长公式可知，

将式(3)～式(6)代入式(2)，可得

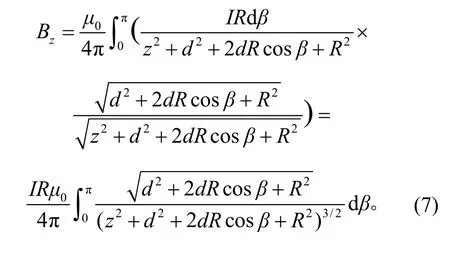
当距离d→0 时，式(7)可简化为

式(8)为单个半圆线圈在原完整线圈轴线上一点的磁感应强度，2 个半圆线圈在该点上的总磁感应强度为

观察可知式(9)与式(2)的结果完全一致。这表明，电流大小和方向一致的2 个半圆线圈，在两端点彼此绝缘的基础上互相靠近直至完全接触时，在组合线圈轴线上产生的磁感应强度等效于一个完整的载流线圈的轴向磁感应强度，如图4所示。

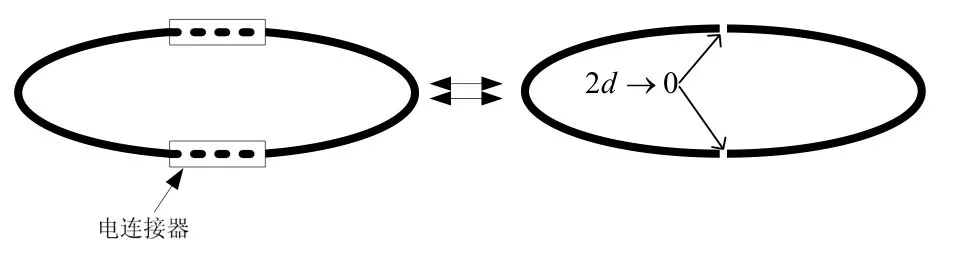
图4 线圈结构等效示意图Fig.4 Schematic diagram of the equivalence of the two kinds of coils

如前所述，图4中每个半圆线圈实际是被分别看作某个闭合回路的一部分，为达本文目的，该闭合回路的剩余部分不应干涉线圈的轴向充退磁磁场，为此，可以将剩余部分回路设计为图5所示结构，图中箭头方向为线圈载流方向。由2 组这样的半圆线圈组成的分离式充退磁线圈如图6所示。

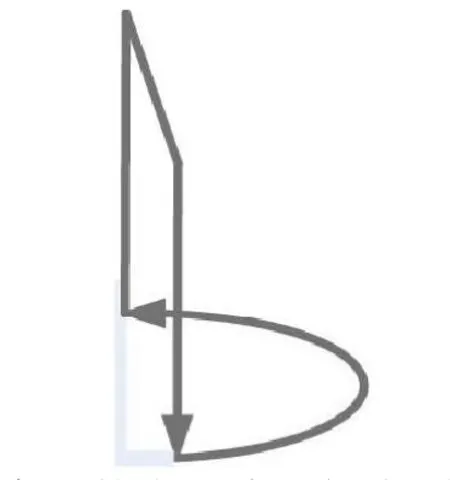
图5 完整的半圆线圈闭合回路Fig.5 The complete closed circuit of the semi-circle coil

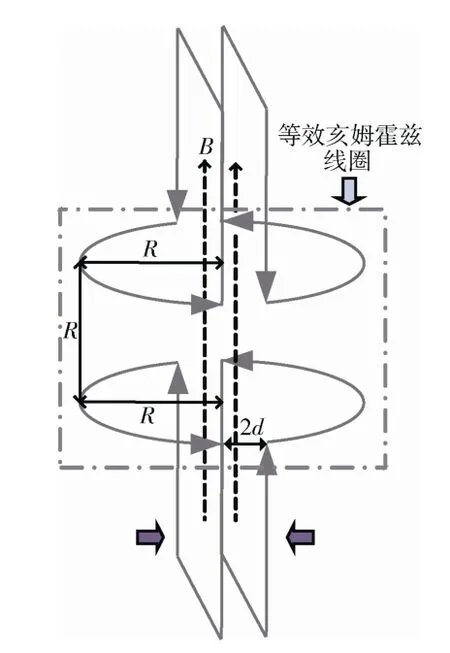
图6 分离式充退磁线圈结构示意图Fig.6 Magnetization-demagnetization coil with no connectors

当d→0 时，与半圆线圈构成完整回路的矩形回路在轴向上的电流合量为0，不会产生干扰磁场。使用时，只需将设备对称的两部分按图中粗箭头方向围绕卫星合拢并通电，组成等效亥姆霍兹线圈，即可获得垂直方向均匀磁场供充退磁试验使用，避免了原设备复杂、耗时的接插工序。

2 电性能估算

分离式充退磁线圈需要与原充退磁电源匹配，这就要求对线圈的电阻、电感等电性能参数进行严格控制，这涉及线圈的匝数、尺寸等主要参数的重新估算。综合考虑后，将线圈组的直径设定为2.9 m，利用磁仿真平台搭建图7所示的线圈组磁场分布计算模型，仿真计算结果如图8所示。

图7 分离式充退磁线圈CST 模型Fig.7 The CST model of the no-connection magnetization- demagnetization coil

通过仿真和计算得到，线圈组的线圈常数为0.05 mT/A，在直径2.0 m 的中心球域内所产生磁场的不均匀度小于15%。由此可知，本文所提出的分离式线圈结构可以在其中心区域产生供退磁试验使用的均匀磁场。若线圈依然使用直径为3.5 mm、电阻率为1.673×10-5Ω·mm 的铜导线，则计算得到线圈的总电阻为3.00 Ω，考虑到其自身的电感量及与充退磁电源的匹配电感，设备的总阻抗不超过3.10 Ω，可以很好地匹配现有的充退磁电源。

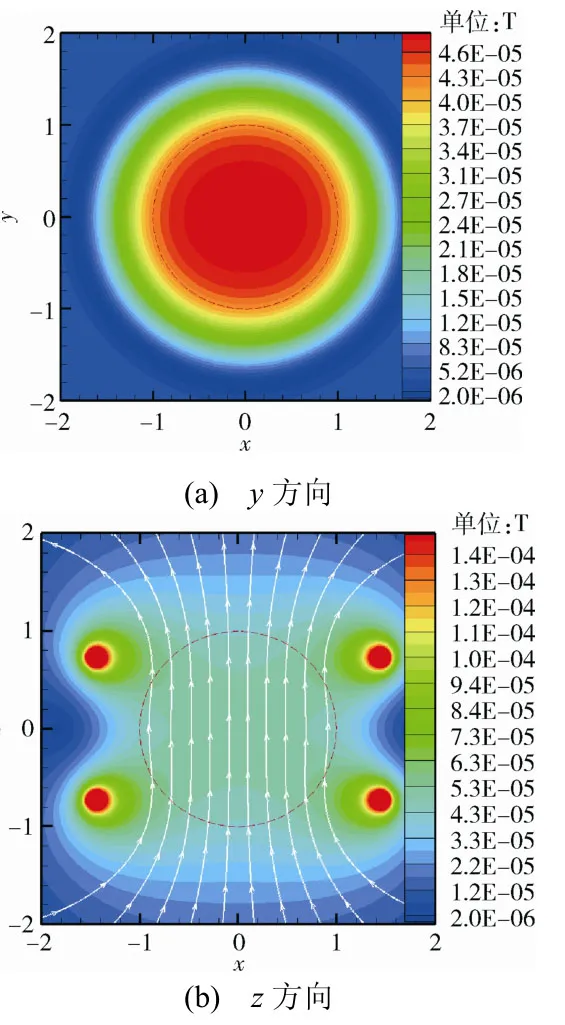
图8 y 方向及z 方向磁场分布仿真Fig.8 Simulation of the y and z direction magnetic field distributions

3 线圈间隙变化对磁场均匀区的影响

在工程实际中2 个半圆线圈不可能实现完全零距离接触，需要留出微小间隙以保证线圈间的绝缘性，由此产生的均匀区误差还需进一步分析。根据磁场不均匀度定义，2 个半圆线圈间隙（2d）变化对磁场均匀区产生的误差影响为Bd=(|B-B0|/B0)×100%，其中B0是线圈中心点处的磁感应强度。

图9是仿真得到的2d=50 mm 时，x-y截面和x-z截面内磁场不均匀度分布，与d=0 的情况相比较，看不出明显变化。为提高可视化效果，图中只显示Bd＜15%的结果，其中：红色虚线圆直径为2.0 m；图9(b)中白色带箭头线是磁力线。x-y截面内的磁场不均匀度分布稍微偏离正圆（红色虚线），这是由于2d沿着横向（即x轴）增大所导致，与理论分析结果完全相符合。

图10和图11分别给出仿真得到的2d变化时（0→5→10→25→50 mm），沿着z轴和x轴的磁场强度分布和磁场不均匀度分布。可以看出，随着2d的增大，沿着z轴和x轴的磁场强度都有减小的趋势，中心区域半径0.5 m 范围内的磁场强度变化小于2%。而d变化时，沿着z轴和x轴方向的磁场不均匀度分布曲线几乎重合，说明2d的变化对于磁场不均匀度影响不大。

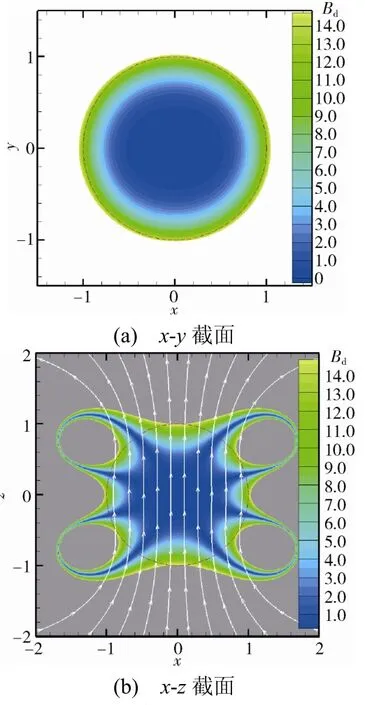
图9 2d=50 mm 时，仿真得到x-y 截面和x-z 截面磁场 不均匀度分布Fig.9 The non-uniformity of the simulated magnetic field of x-y section and x-z section (2d=50 mm)

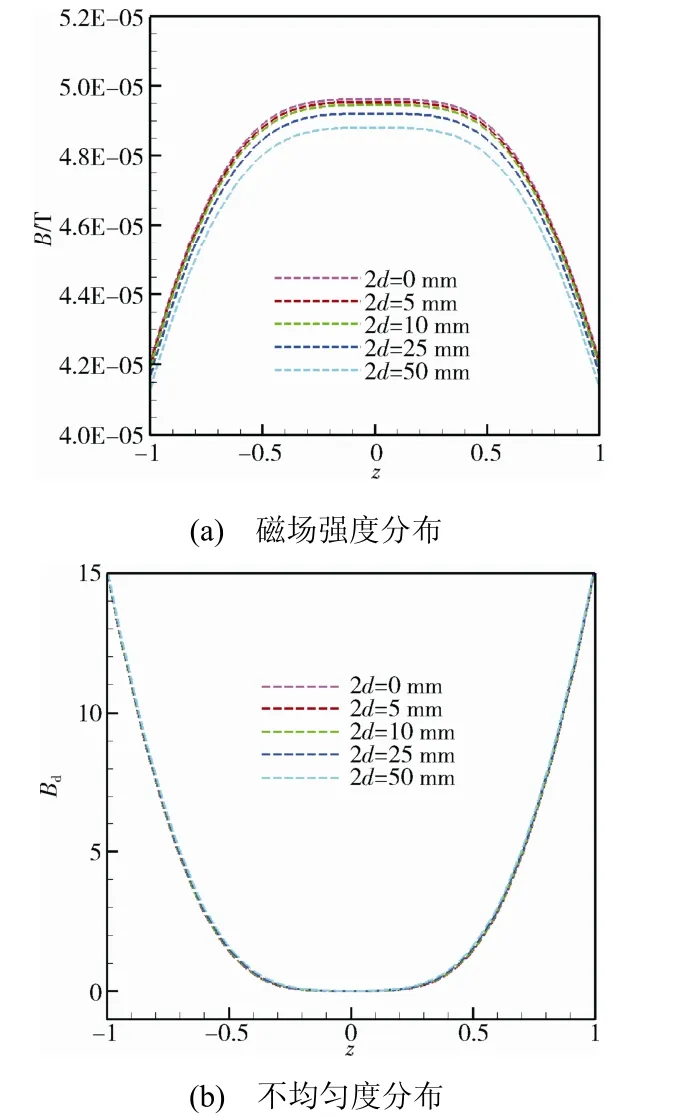
图10 2d 变化时，仿真得到的z 轴的磁场强度分布和 磁场不均匀度分布Fig.10 The distribution of simulated magnetic field intensities and the non-uniformity of the magnetic field along z-axis against 2d

图11 2d 变化时，仿真得到的x 轴的磁场强度分布和 磁场不均匀度分布Fig.11 The distribution of simulated magnetic field intensities and the non-uniformity of the magnetic field along x-axis against 2d

表1列出计算得到的三维空间内磁场不均匀度小于15%区域的体积与2d的关系。可以看出，2d从0 增加到50 mm，磁场不均匀度小于15%区域的三维空间体积变化值小于2%，可见，当2d在0～50 mm范围内变化时对于磁场均匀度几乎没有影响。

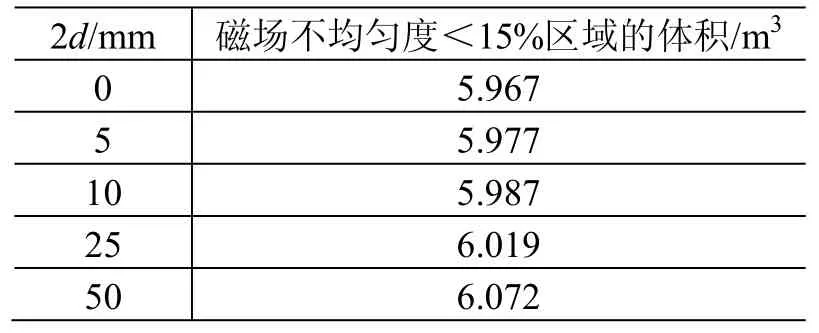
表1 磁场不均匀度小于15%区域的体积与2d 的关系Table 1 The volume of the nonuniformity of the magnetic field less than 15% vs.2d

4 结束语

本文通过理论推导，提出了一种全新的分离式垂直方向充退磁线圈结构，并通过仿真计算验证了该结构的可行性。在使用时，只需将线圈的两部分靠近合拢即可开始充退磁试验，避免了较为繁琐的接插工序，大幅缩短了试验时间。由于工程原因，为保证线圈间的绝缘性，2 个半圆线圈间需要留出微小间隙。仿真表明当该间隙不大于50 mm 时，磁感应强度和磁场均匀度仍然能满足试验要求。

（References）

[1]赵凯华, 陈熙谋.电磁学[M].北京∶高等教育出版社, 1985∶352-367

[2]易忠.卫星整星充、退磁机理研究[J].航天器环境工程, 2003, 20(4)∶1-12 Yi Zhong.Research of magnetizing and demagnetizing mechanism of satellites[J].Spacecraft Environment Engineering, 2003, 20(4)∶1-12

[3]Harris C A.Demagnetization methods for spacecraft system and components, NASA reports N69-33978[R], 1969

[4]齐燕文.空间磁环境模拟技术[J].航天器环境工程, 2005, 22(1)∶19-21Qi Yanwen.Space magnetic environment simulation technology[J].Spacecraft Environment Engineering, 2005, 22(1)∶19-21

[5]王陈琪, 史尧宜, 齐燕文, 等.卫星垂直方向充退磁线圈设计新方法[J].航天器环境工程, 2008, 25(6)∶594-597 Wang Chenqi, Shi Yaoyi, Qi Yanwen, et al.A new method of designing vertical magnetization- demagnetization coil for satellite[J].Spacecraft Environment Engineering, 2008, 25(6)∶594-597