智能的图像滤波去噪算法
2015-12-20邓潇潇
杜 慧,邓潇潇,李 建,宋 科
(西南石油大学 计算机科学学院,四川 成都610500)
0 引 言
在获取图像的过程当中,由于各种因素的干扰会给图像带来噪声,表现为各种形式的干扰点或是条纹,所以保证图像受污染程度最小成为数字图像处理领域的重要部分。图像一旦有了噪声之后大大降低了质量,同时信息会受到干扰,在对图像进行边缘检测、分割、提取信息之前必须对图像进行滤波操作,消除噪声对图像的干扰。产生的噪声原因有多种:一种是由于环境影响产生的,例如在运输过程中造成图像的污损、破裂等,这种情况是不能通过去噪算法完全去除的,只能通过图像自身的纠错算法进行纠错;另一种是由采集图像的设备自身产生的,也就是盐粒噪声,符合泊松分布,所以也被称为泊松噪声。目前,图像的去噪方法有多种,最常用的两种是均值滤波与中值滤波,它们对不同的噪声有不同的去噪能力。实际图像处理过程中,虽然可以有效的控制噪声,但是对图像的边缘没有起到有效的保护作用,使得图像的边缘变得模糊。因此本文针对这一问题,提出了一种智能的图像滤波去噪算法。经过改进后的噪声消除算法与传统算法相比,图像干扰信息大幅度降低而且边缘信息保持完整,对图像识别带来方便。文献 [1-5]着重讲述了改进的滤波去噪算法,这些算法为学者学习滤波去噪算法提供了有力借鉴及一定帮助。
1 图像的灰度化
现在的采集设备一般是彩色装备,很少有黑白的,所以采集到的图片基本都是彩色图像。彩色图像的每个像素均有3个颜色分量R、G、B,每一个分量都有255个值[6],算起来每一个像素则有惊人的255×255×255种像素变化,信息量比较大,储存起来需要较大的空间,处理相对来讲比较麻烦,时间也较久。而灰色图像只有黑白两色,只能有255个像素的变化,所含的信息量要少于彩色图片,并在图像识别过程中,彩色信息对图像识别没有影响。为了提高效率,减少系统的内存消耗,加快去噪算法的速度,需要对采集到的图像进行灰度处理,这样可以在一定程度上降低图像处理的计算量[7]。目前图像灰度化算法主要有平均值法、最大值法、加权平均法、基于梯度域的算法[8]以及基于TV 复原模型改进的sapiro算法[9]等。
考虑到图像去噪过程需快速和准确,本文采用加权YUV 灰度转换算法。设某像素的彩色分量值分别为 (R,G,B),其中0≤R≤255,0≤G≤255,0≤B≤255,则可通过式 (1)将彩色图像的分量值 (R,G,B)转换成灰度图像的灰度值W
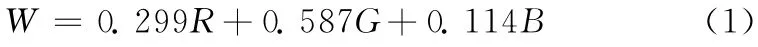
经过实验结果表明,该算法在处理图像的灰度化方面取得了令人满意的效果。在使用了该算法后,灰度变换后的图像能够保留识别的一些必要的信息。图1为彩色图像灰度化后的图像。

图1 彩色图像灰度化后的图像
2 常用滤波去噪算法
根据噪声和信号与噪声之间的关系可分为加性噪声和乘性噪声。加性噪声指噪声的数据信息与图像的信号无关。设图像信号为g(x,y),噪声数据为n(x,y),含噪图像为f(x,y),则f(x,y)=g(x,y)+n(x,y)。信道噪声就是加性噪声。乘性噪声指它的噪声数据信息与图像的信号有关联,则 含 噪 图 像f(x,y)=g(x,y)+n(x,y)×g(x,y)[10]。常用的滤波除噪方法有很多种,包括均值滤波法、最大最小值法、中值滤波法、挖芯算法、高斯滤波法等,经常用的有均值滤波法和中值滤波法。
2.1 均值滤波法
均值滤波算法定义请参见文献 [1]。利用一个滑动的窗口对采集到的图像进行逐像素的移动,令窗口内所有像素的平均值为窗口中心点的像素值。设某一像素 (x,y)位于图像f(m,n)中,其领域c,设c有k 个像素,则像素(x,y)的灰度值为c内所有像素的平均值。在图像处理过程中,c的形状和大小一般是保持不变的,但是有时候也会根据图像变化而变化。像素 (x,y)一般位于c的中心位置。设方差为σ2。
运用领域平均法后,可以得到图像f 为
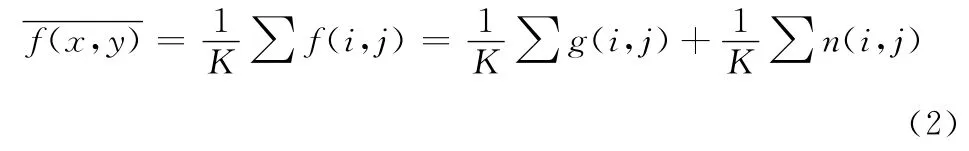
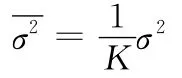

图2 原噪声图像

图3 均值滤波处理后图像
由图2,图3对比可以得出,使用均值滤波算法后虽然噪声能够控制住,但是均值滤波削弱了图像的边缘,使图像明显变得有些模糊。
2.2 中值滤波法
中值滤波是常用的非线性滤波方法,定义请参见文献[2]。中值滤波器是Turky于1971年提出的,它是采用n×n像素的窗口,在图像表面逐行滑动,将所有像素的中间值作为像素点的灰度值[11]。图4为中值滤波算法的流程。
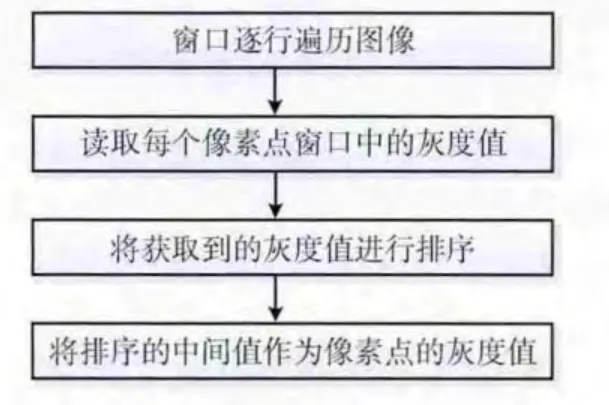
图4 中值滤波流程
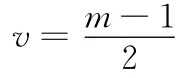
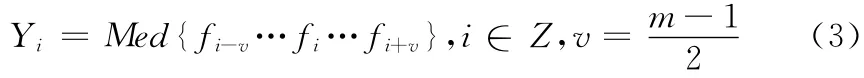
假设有一组一维序列为 {4,6,2,0,9},那么经过排列后序列为{0,2,4,6,9},则它的最终滤波输出为4。
在对二维序列进行中值滤波时,滤波器窗口是二维的,不过在这里可采用多种不同的窗口形状,如线性状、正方形、圆形、十字形等[12]。二维数据的中值滤波可表示为

在选择滑动窗口时,窗口的尺寸一般定为奇数,可以有3*3,5*5,7*7等,且一般会先从最小值3开始。若效果不满意再选择大的尺寸,慢慢进行实验,直到最后达到令人满意的效果。
中值滤波的方法运算比较简单,而且很容易实现,处理速度快,不过它的缺点就是不能有效地保护图像的边缘。选择的滑动窗口的大小和形状会直接影响到滤波的最终效果:较大尺寸的滑动窗口可以达到很好的去除噪声的效果,但是会丢失图像的边缘信息,小尺寸的滑动窗口能够有效地保护好图像的边缘信息,但是这样子它的滤波效果令人不甚满意。图5为常用窗口与对应的输入图形。
由图6,图7可以看出当使用中值滤波后,噪声已被控制的差不多,但是图像的信息却没有很好的得到保护,使得图像变得有些模糊。
本文在中值滤波和均值滤波算法的基础上提出了一种既能保持边缘细节的清晰度,又能很好的滤除噪声的算法。
3 智能的滤波去噪算法
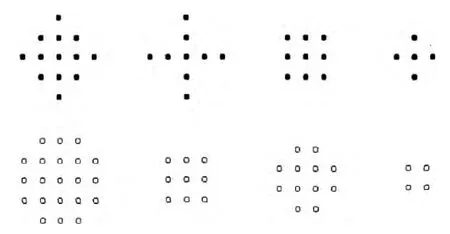
图5 常用窗口与对应的输入图形

图6 原噪声图像

图7 中值滤波处理后图像
传统的噪声消除算法用到了局部滤波,包括均值滤波法、最大最小值法、中值滤波法,挖芯算法,也有的用到了高斯滤波法,而现阶段的图像识别已经越来越多的使用彩色图像,而图像中包含了大量的孤立噪声、边缘毛刺、划痕等噪声。
对于上述噪声的消除,孤立噪声或者尖锐噪声,都是比较有效的,但相对来说对边缘的损伤很严重,增加了识别的难度和减小了识别的精确度,这是识别工作所不希望看到的。而对毛刺边缘以及划痕,这些方法能够滤除一部分,但当毛刺和划痕在边缘附近或者和边缘粘连时,这些方法会将部分边缘误判为噪声而被滤除,同时边缘模糊也比较严重,为了保持边缘细节的清晰度,又很好的滤除噪声,本文经过对噪声和边缘的特点分析提出了一种能智能的判断边缘细节和带噪声的平滑区域的综合改进算法。
中值滤波对对脉冲噪声比较有效,但方向性很差;均值滤波可以平滑图像,但不能去除噪声,只能削弱;挖心算法只对孤立噪声有效;高斯滤波是基于频域的平滑滤波器,是一个局部滤波器,但单独使用传统的高斯滤波器对图像噪声进行消除仍存在不足,考虑到这几种滤波器的特点,希望能有一种滤波算法综合这些滤波器的优点而排出其对图像边缘信息的破坏,首先必须对图像局部结构进行分析,识别出边缘纹理、平滑区域以及噪声,在数学中正好有一种算法能很好的解决这种问题,在数学中用方差来描述随机变量对于数学期望的偏离程度,而在这里也可以用该方法来计算某一像素点相对于局部区域的导向,从而判断该点的偏离程度区分出该点是处于该区域的平滑区还是边缘纹理区,该公式表示如下
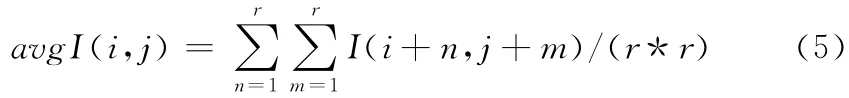
式中:i,j——要计算的像素点所在图像中的坐标,n,m——宽高分别为r的窗内在坐标,I——要计算的像素点的值,avgI——在r*r的窗中的所有像素值的平均值
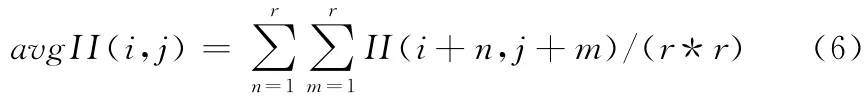
式中:avgII——了在窗r*r范围内的像素平方的均值。
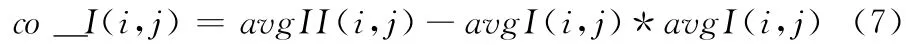
为了很好的将边缘纹理与平滑区域判别出来并减少判断失误,将co_I 作为边缘纹理区和平滑区的一个判决因子,而在实际的图像拍摄过程中,因环境等的影响,环境对图像采集的准确率印象占到0.8%左右,所以为了表示该计算的像素点与周围区域像素点的准确情况,可以用该环境影响进行校正,如下式表示
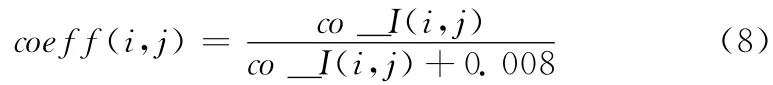
式中:coeff——离差的系数,0.008——修正系数。
有了离差系数,可以自适应的对图像中的像素点进行判断,将纹理边缘和平滑区区分开来,既保护了边缘细节,同时消除了噪声,处理过程如下式
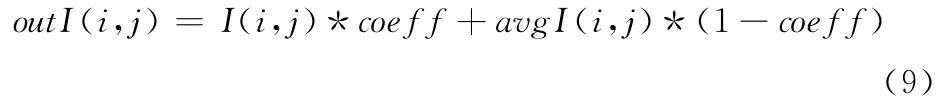
式中:outI——计算后的输出像素值,从式 (9)可以看出,当一个像素点处于边缘纹理区时,在这个区域内co_I 将会很大 (根据边缘区域与平滑区域的特性式 (7)计算),近似为1,从而由式 (8)得到coeff 无限趋近于1;而孤立点脉冲噪声或边缘毛刺其数量比较少,在区域面积达到一定数量时,经过均方,这些噪声也近似为平滑区 (即进行了能量扩散),从而co_I 很小,近似为0,从而coeff 无限趋近于0;而平滑区的coeff 可以认为为0;由这些可以看出,当计算像素点处于边缘纹理区域时,coeff 近似为1,则输出像素值outI近似等于输入像素值I,即outI(i,j)=I(i,j)*1+avgI(i,j)*(1-1)=I(i,j)从而对边缘不会出现破坏作用,而当被计算点处于平滑区或者有噪声点存在时由式 (8),coeff 近似等于0,则有outI(i,j)=I(i,j)*(1-1)+avgI(i,j)*(1-0)=avgI(i,j),则表现的是均值,若该点是噪声点也因为平均的原因使得该点的像素值近似等于周围平滑区域的值,从而消除了噪声。图8,图9为运用本文的算法后含噪图像滤波前后对比。

图8 含噪图像

图9 滤波除噪后的图像
由图8、图9对比可得出,图像的噪声得到了很好的抑制,而且并没有对图像造成影响,取得了令人满意的效果。
4 实验结果对比
在对图像去噪效果评价时,对于边缘信息和图像纹理细节的保持通过主观目测来评价。而对于噪声的抑制效果主要采用均方差MSE、归一化均方差NMSE、等效视数ENL以及峰值信噪比PSNR 等评价指标[13]。其中,NMSE表征了去噪图像的失真程度;ENL 为均值的平方与方差的比值,能够衡量图像的斑点噪声相对强度,反应了滤波算法的斑点抑制能力;PSNR 是最大像素值与噪声强度的比值[14]。表1为对比数据详情。
由表1中可以得出,在峰值信噪比PSNR 上,本文提出的智能算法的结果是最高的,这体现了良好的滤波效果以及去噪能力。而在均方差MSE 和归一化NMSE 和等效视数ENL中,本文提出的算法的结果都偏低,但是这并不影响图像信息的识别。
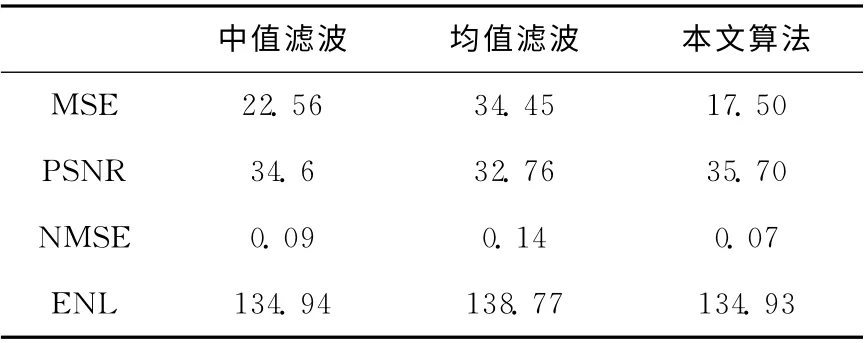
表1 3种算法去噪的性能指标
5 结束语
传统的去噪算法虽然可以有效的控制噪声,但图像去噪之后,图像的边缘变得模糊。本文经过对噪声和边缘的特点分析提出了一种能智能的判断边缘细节和带噪声的平滑区域的综合改进算法。该算法自适应的对图像中的像素点进行判断,将纹理边缘和平滑区区分开来,从而消除噪声。实验结果表明,本文所提出的算法不仅可以消除噪声,而且可以保留图像的边缘信息。最重要的是,可以智能的判断出边缘细节和带噪声的平滑区域,且对噪声图像具有很好的滤波效果。
[1]LIU Guohong,GUO Wenming.Application of improved arithmetic of median filtering denoising [J].Computer Engineering and Applications,2010,46 (10):187-189 (in Chinese).[刘国宏,郭文明.改进的中值滤波去噪算法应用分析 [J].计算机工程与应用,2010,46 (10):187-189.]
[2]ZHANG Maonv,LIU Wei.An improved median filter denoising based on edge detection [J].Computer and Modernization,2011,187 (3):63-65(in Chinese).[张毛女,柳薇.一种基于边缘检测的改进的中值滤波去噪方法 [J].计算机与现代化,2011,187 (3):63-65.]
[3]XIAO Chunsheng,WANG Xiaotong,XU Xiaogang,et al.The de-noising algorithm of filtering based on empirical mode decomposition [J].Ship Science and Technology,2010,32(10):41-44 (in Chinese). [肖春生,王孝通,徐晓刚,等.基于经验模式分解的滤波去噪算法 [J].舰船科学技术,2010,32 (10):41-44.]
[4]FAN Hanqi,MIAO Lanfang,ZHANG Xin,et al.Robust high-order bilateral denoising filter[J].Journal of Computer-Aided Design & Computer Graphics,2009,21 (6):812-818(in Chinese).[范涵奇,苗兰芳,张鑫,等.鲁棒的高阶双边滤波去噪算法 [J].计算机辅助设计与图形学学报,2009,21(6):812-818.]
[5]ZHANG Xin,WANG Zhangye,FAN Hanqi,et al.A feature preserving denoising approach for scanned models based on trilateral filtering [J].Journal of Computer-Aided Design &Computer Graphics,2009,21 (7):936-942 (in Chinese).[张鑫,王章野,范涵奇,等.保特征的三维模型的三边滤波去噪算法 [J].计算机辅助设计与图形学学报,2009,21(7):936-942.]
[6]CAO Jianqiu,XIAO Huarong,LAN Zhangli,et al.Chaos encryption algorithm based on bit-plane of digital image [J].Computer Technology and Development,2010,20 (8):133-136 (in Chinese).[曹建秋,肖华荣,蓝章礼,等.基于数字图像比特面的混沌加密方法 [J].计算机技术与发展,2010,20 (8):133-136.]
[7]Wakahara T,Yamamoto N,Ochi H.Image processing of dotted picture in the QR code of cellular phone[C]//Proceedings of the IEEE International Conference on P2P,Parallel,Grid,Cloud and Internet Computing,2010:454-458.
[8]ZHANG Weixiang,ZHOU Bingfeng.A color to gray method based on gradient domain [J].Image Technology,2007,18 (3):20-22(in Chinese).[章卫祥,周秉锋.一种基于梯度域的彩色图像转灰度图像的方法[J].影像技术,2007,18(3):20-22.]
[9]GUO Yanling,PENG Jinye,WANG Dakai.Transformation of color image to gray image based on improved total variation restoration model [J].Computer Engineering and Applications,2009,45 (7):192-194 (in Chinese). [郭彦伶,彭进业,王大凯.改进TV 复原模型的彩色-灰度图像变换方法[J].计算机工程与应用,2009,45 (7):192-194.]
[10]CAI Xuesen,DAI Jinbo,LI Xiaoning.Median filter method and average value filter method in the application of bar code denoising [J].Journal of Changchun Normal University(Natural Science),2008,27 (4):40-42 (in Chinese). [蔡学森,戴金波,李晓宁.中值滤波与均值滤波法在条形码去噪中的应用 [J].长春师范学院学报 (自然科学版),2008,27 (4):40-42.]
[11]Jin L H,Li D H.A switching vector median filter based on the CIELAB color space for color image restoration[J].Signal Process,2007,87 (1):1345-1354.
[12]WU Degang,ZHAO Liping.A filtering algorithm for removing image mixed noise [J].Computer Engineering and Design,2014,33 (9):11-13 (in Chinese). [吴德刚,赵利平.一种去除图像混合噪声的滤波算法 [J].自动化仪表,2014,33 (9):11-13.]
[13]Dore V,Cheriet M.Robust NL-means filter with optimal pixelwise smoothing parameter for statistical image denosing[J].IEEE Transactions on Signal Processing,2009,57(5):1703-1716.
[14]QIAO Ziliang,DU Huimin.NL-MEANS algorithm based on K-means clustering for ultrasound image de-noising [J].Computer Engineering and Design,2014,35 (3):940-942 (in Chinese).[乔子良,杜慧敏.基于K 均值聚类NL_MEANS算法的超声图像去噪 [J].计算机工程与设计,2014,35(3):940-942.]
