基于随机搜索策略的人工蜂群算法

王志刚，尚旭东

（南京师范大学泰州学院 数学科学与应用学院，江苏 泰州225300）

0 引 言

人工蜂群 （artificial bee colony，ABC）算法［1－4］作为一种随机优化算法，同其它一些随机优化算法一样，其本身存在一些缺陷，如收敛速度较慢、求解复杂多峰函数时容易陷入局部最优。为此，专家们分别从不同方面提出了相应的策略来改善算法的性能［5－11］。文献 ［5］在ABC算法中利用混沌运动的随机性和遍历性来提高算法的全局搜索能力；文献 ［6］通过引入Rosenbrock旋转方向的办法对引领蜂的搜索策略进行改进，提高了算法的收敛速度；文献［7］受粒子群算法的启发，给出一个新的搜索算子来加快算法的收敛速度；文献 ［8］提出一种双种群差分蜂群算法，将种群中的个体随机分成两组，每组采用不同的优化策略同时进行寻优；文献 ［9］通过引入混沌映射提出了带混沌局部搜索的人工蜂群算法；文献 ［10］采用混沌映射和反向学习理论初始化种群，然后引入差分变异搜索机制和一个平衡选择两种搜索机制的概率，以提高算法的全局进化性能；文献 ［11］在ABC算法的搜索策略中通过引入一个扰动概率参数和自适应尺度因子来对ABC 算法进行改进，这些改进算法都在一定程度上改善了ABC 算法的性能，但仍存在易陷入局部最优的不足。

在前人研究的基础上，本文提出一种基于随机搜索策略的人工蜂群算法。算法在蜂群搜索过程中借鉴差分进化算法的交叉操作，并采用随机选择的方式来进行搜索，同时在搜索过程中加入一定的扰动来增强种群的多样性。基于8个标准测试函数的仿真结果表明，与ABC 算法和其它一些改进的ABC算法相比，该算法寻优精度高、收敛速度快、鲁棒性强。

1 人工蜂群算法

ABC算法中，人工蜂群包含引领蜂、跟随蜂和侦察蜂3个部分。人工蜂群算法在求解优化问题时，食物源代表优化问题的一个可能解，蜂群采蜜 （食物源）的过程也就是搜寻优化问题最优解的过程。食物源的优劣取决于优化问题的适应值 （函数值），适应值高的食物源较优。人工蜂群算法中解的个数 （SN ）等于引领蜂或跟随蜂的个数。用xi＝（xi1，xi2，…，xiD）表示第i个食物源 （i＝1，2，…，SN，D 为搜索空间的维数）。人工蜂群搜索食物源的过程如下：①引领蜂对当前食物源进行邻域搜索，产生候选食物源，并通过贪婪选择较优的食物源；②跟随蜂根据引领蜂分享的信息选择一个食物源，进行邻域搜索产生候选食物源，并通过贪婪选择较优的食物源；③引领蜂放弃食物源，变为侦察蜂，并随机搜索新的食物源。

引领蜂和跟随蜂根据下式在食物源的邻域生成一个候选食物源

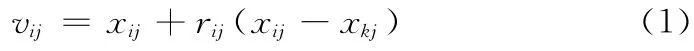
式中：vij——生 成 的 候 选 食 物 源，k ∈｛1，2，…，SN｝，j ∈｛1，2，…，D｝，这两个数都是随机选取的，但k≠i，rij是［－1，1］上均匀分布的随机数。式 （1）称为ABC 算法的搜索策略。

跟随蜂通过如下概率来选择食物源

式中：fiti——第i个食物源的适应值。在最小化问题中，fiti与优化问题目标函数值fi的对应关系为

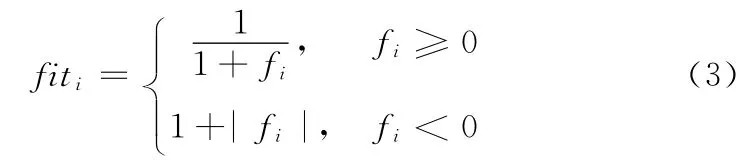
在ABC算法中，如果连续经过limit 次循环之后食物源仍然没有得到更新，则引领蜂就放弃食物源，转变为侦察蜂，并按下式随机产生一个新的食物源

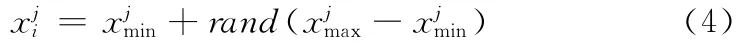
2 基于随机搜索策略的人工蜂群算法

在式 （1）中，由于rij是［－1，1］上均匀分布的随机数且xkj为随机选取的种群中的个体的一个分量，使得该搜索策略具有较好的全局搜索能力，但却忽略了算法的局部搜索能力，使算法的收敛速度较慢［7］。为此，文献 ［7］提出了一种新的搜索策略来对式 （1）进行改进

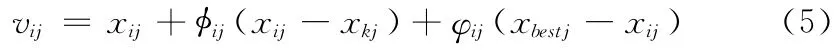
其中，k，j选取与式 （1）相同，ij 是［－1，1］上均匀分布的随机数，φij 为［0，1.5］之间的随机数，xbest为种群最优解。由式 （5）可以看出，由于有最优解xbest的引导，上述搜索策略既保证了算法具有较强的全局搜索能力，同时，在一定程度上也提高了算法的局部搜索能力。为进一步提高算法的局部搜索能力，可以将式 （5）变化为

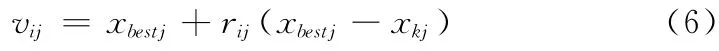
与式 （1）、式 （5）相比，式 （6）由于有种群最优解引导种群的搜索轨迹并且仅在最优解附近产生新的候选解，从而比式 （1）、式 （5）更能提高算法的局部搜索能力，但容易陷入局部最优。

从上面的分析可以看出，式 （1）全局搜索能力较强，但局部搜索能力较弱；而式 （6）局部搜索能力较强，全局搜索能力较弱。众所周知，全局搜索能力和局部搜索能力对智能优化算法是非常必要的，因此，如何平衡全局搜索能力和局部搜索能力是智能优化算法获得较高性能的关键。在对式（1）和式（6）两种搜索策略进行分析的基础上，结合式（1）全局搜索能力较强的优点和式 （6）局部搜索能力较强的优点，本文采用不确定的随机方式来选择搜索策略，即

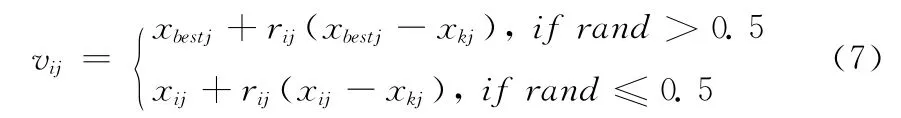
其中，rand 为（0，1）之间均匀分布的随机数，由式 （7）可以看出，上述搜索策略改变了ABC 算法原有搜索策略的固定模式，结合了式 （1）和式 （6）两种搜索策略，对搜索策略进行随机选择，增强了算法的大范围搜索。

同时，为增加种群多样性，防止算法陷入局部最优，我们对在搜索过程中进行小概率的扰动，即当随机数满足一个小概率时，则进行扰动，增强算法跳出局部最优的能力。扰动方式如下

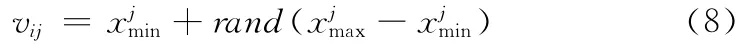
为将随机搜索策略和扰动操作进行有效结合，我们设置一个参数DR（发生扰动是小概率事件，因此DR 取值一般要较大，本文取DR ＝0.9995），对随机搜索策略和扰动进行随机选择，方式如下：

此外，在式 （1）中，引领蜂和跟随蜂只对xij作一维邻域搜索，这导致算法的搜索效率较低，借鉴差分进化算法［12］的交叉操作，本文通过引入一个参数CR 来控制引领蜂和跟随蜂对xij的搜索维数，具体方式如下

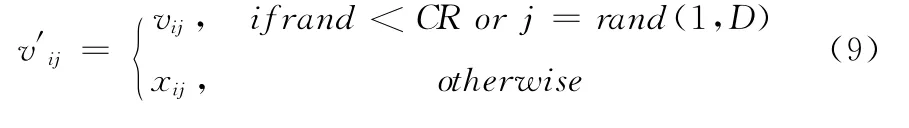
其中，

式中：rij是［－1，1］上均匀分布的随机数，rand 和rand1均为 （0，1）之间均匀分布的随机数，rand（1，D）为［1，D］之间的随机整数。

3 仿真实验

为了验证本文算法的性能，选择8个典型的测试函数用于仿真实验，对ABC 算法、文献 ［7］提出的算法 （记为GABC）、采用式 （6）作为搜索策略的ABC 算法 （记为ABCbest）以及本文算法 （记为ABCRSS）进行比较和分析。实验时，当函数维数为30时，4种算法的种群规模均为SN ＝50，维数为100时，种群规模均为SN ＝100。4种算法中limit ＝100，在ABCRSS 中，对于f1（x）～f4（x），CR ＝0.9；对于f5（x）～f8（x），CR ＝0.0005。表1给出了8 个基准测试函数 （f1（x）～f4（x）为单峰函数；f5（x）～f8（x）为多峰函数）的表达式、搜索范围和理论最优值。

表1 经典测试函数

Best、Worst、Mean和Std分别为算法独立实验10次的最优值、最差值、平均值和标准差。Mean反映了在给定的函数评价次数下算法所能达到的精度，Std反映了算法的稳定性和鲁棒性。表2为4种算法对8个测试函数分别独立运行10次得到的测试结果。图1～图8分别给出8个测试函数在30维时的平均适应值收敛曲线。

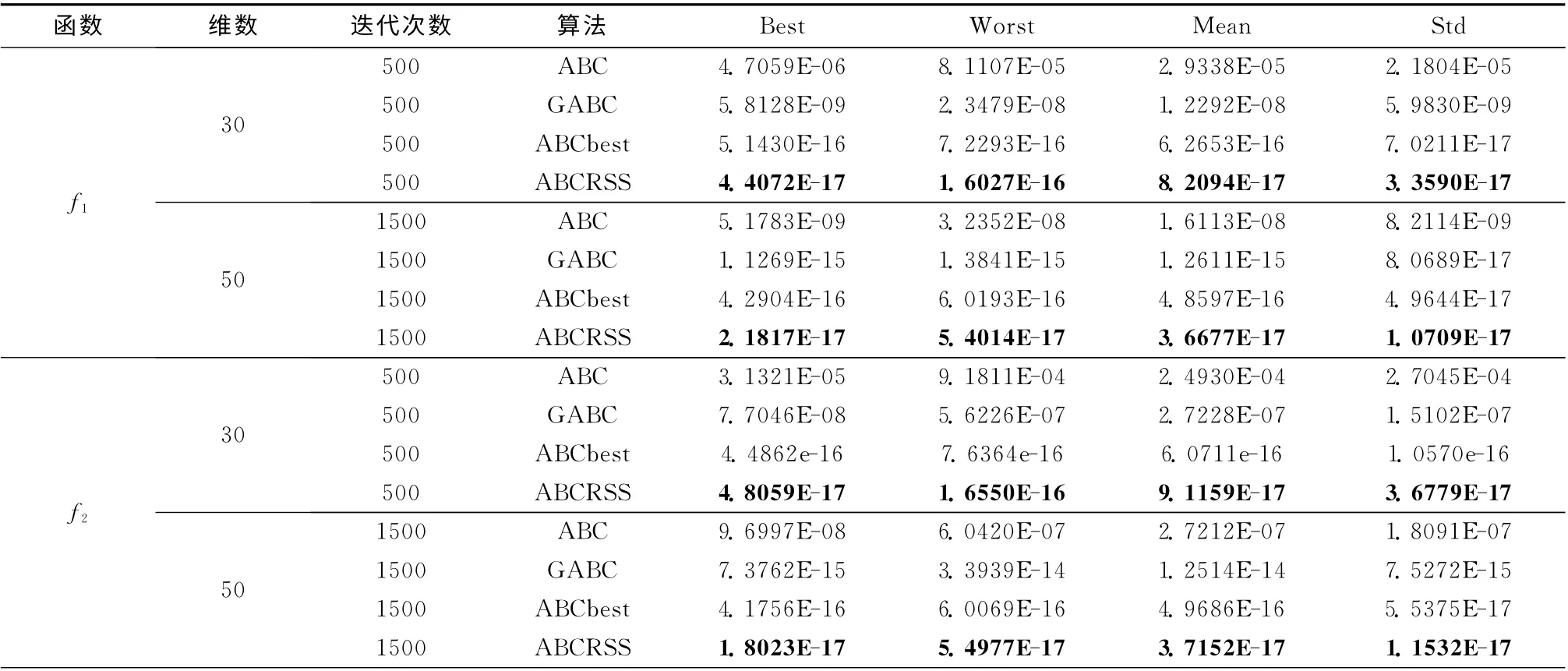
表2 4种算法的实验结果

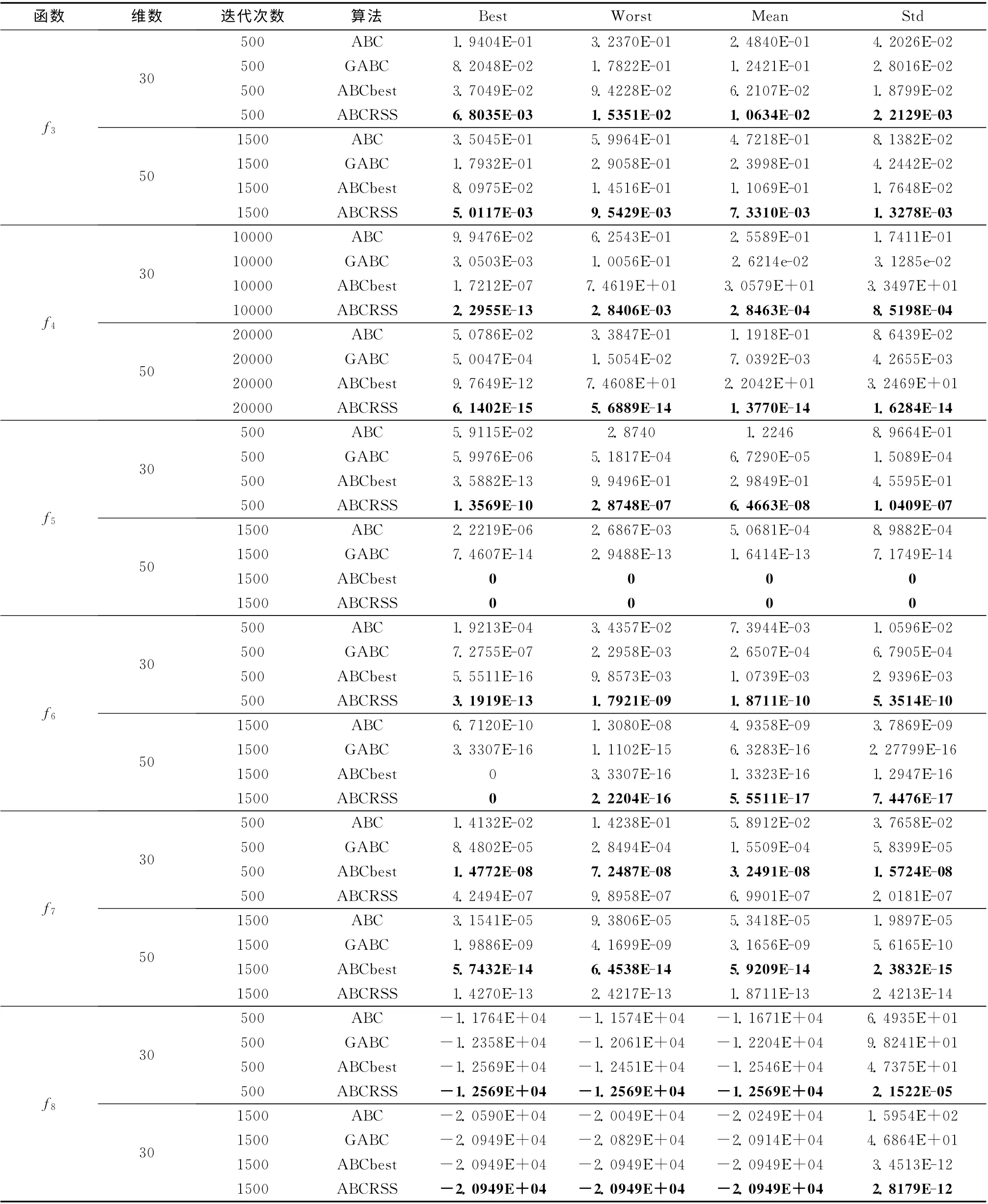
表2 （续）

对于简单的单峰函数f1（x）～f2（x），由表2及图1和图2中可知，4种算法的收敛速度都比较快，但本文算法的收敛速度最快，明显优于ABC 算法、GABC 和ABCbest，且计算精度更高。对于f3（x），4种算法在进化前期收敛速度都很快，在进化后期收敛速度明显减慢，但ABCRSS依然优于其它3种算法，且稳定性也好于其它3种算法。对于十分复杂的非线性函数f4（x），很多优化算法对此函数的求解精度都较低，从图4 中可以看出，ABC 算法、GABC和ABCbest在进化后期基本上停止进化，而本文算法虽然在进化前期收敛速度逊于ABC 算法、GABC 和ABCbest，但在后期却能持续进化，求解结果远优于它们。

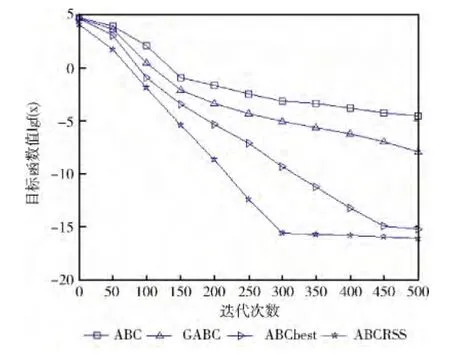
图1 Sphere函数收敛曲线

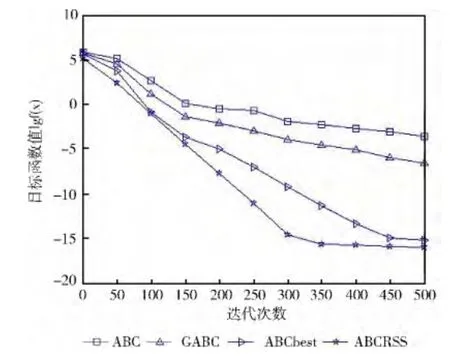
图2 Sum Squares函数收敛曲线

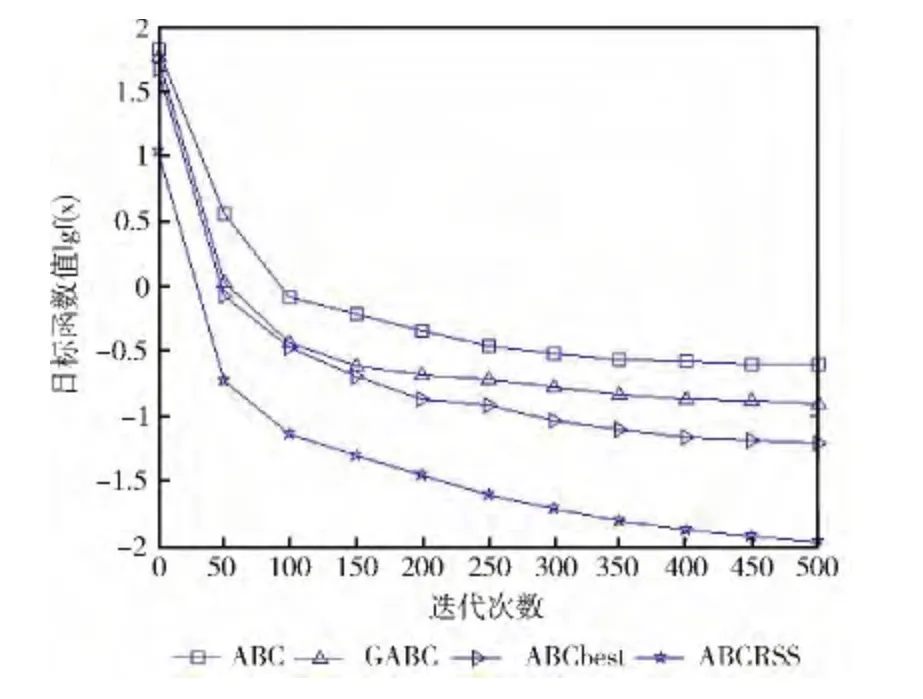
图3 Quartic函数收敛曲线

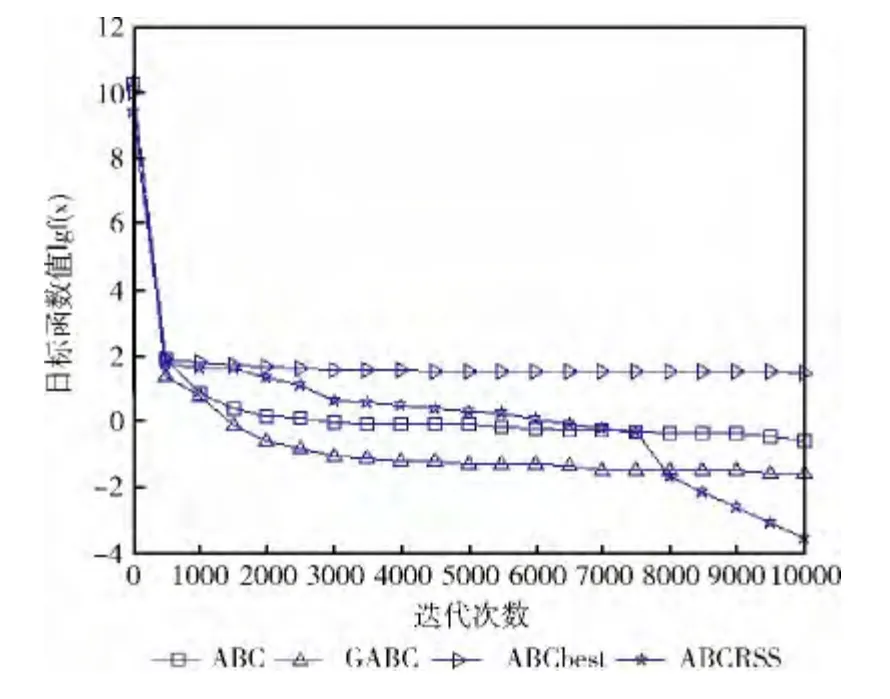
图4 Rosenbrock函数收敛曲线

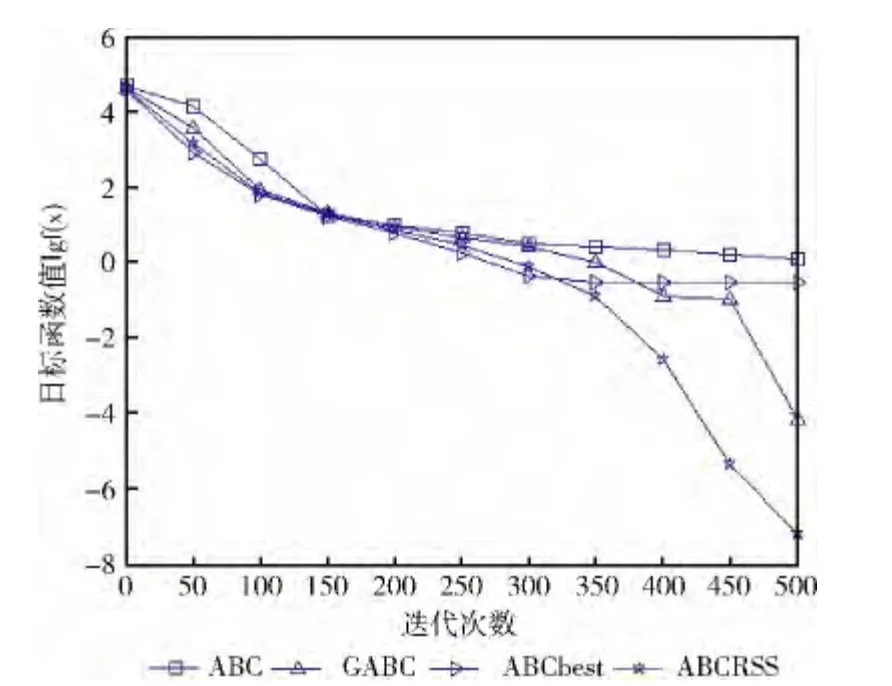
图5 Rastrigin函数收敛曲线

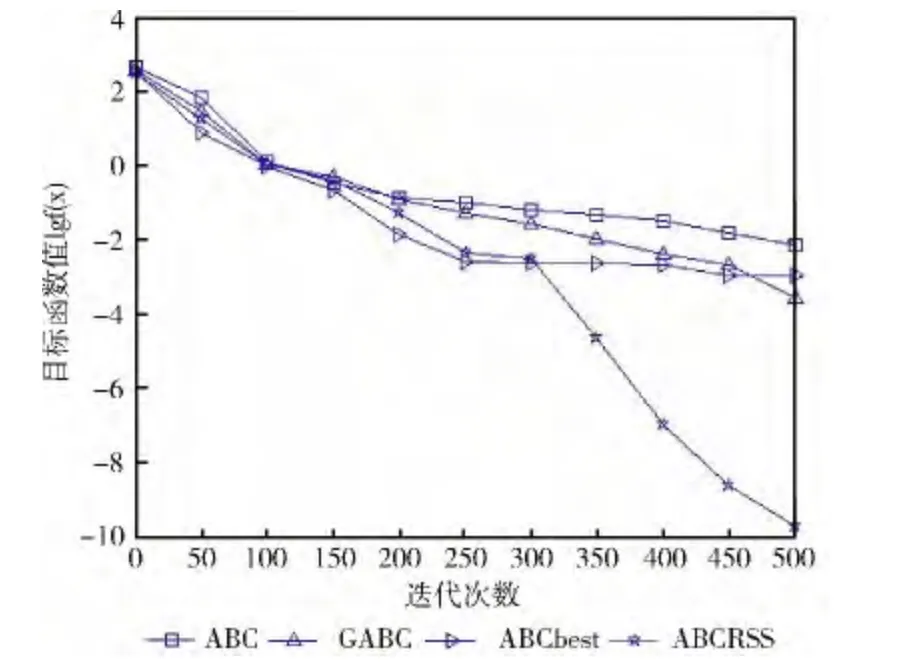
图6 Griewank函数收敛曲线

对于复杂的非线性多峰函数，从表2 可以看出，ABCRSS对于f7（x）的求解结果不如ABCbest，而对于其余3个函数，ABCRSS的求解结果都要优于ABC 算法、GABC和ABCbest。由于这4个函数本身的特性，ABC 算法因为局部搜索能力较弱从而使得它的收敛速度较慢，导致算法的计算精度不高，GABC中由于加入了种群最优解的引导，在一定程度上可以提高算法的计算精度和收敛速度，ABCbest虽然具有很快的收敛速度，但当函数比较复杂时却容易陷入局部最优 （如函数f5（x）和f6（x）），而ABCRSS较好地平衡了算法的局部搜索能力和全局搜索能力，同时通过扰动增强了种群的多样性，使算法能跳出函数中大量的局部最优点陷阱。

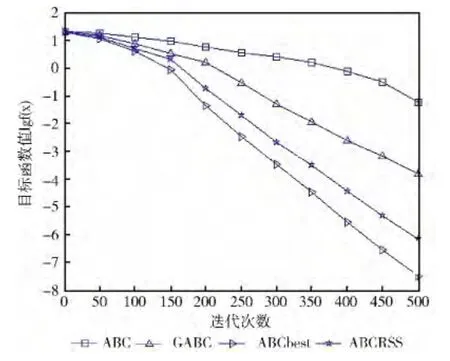
图7 Ackley函数收敛曲线

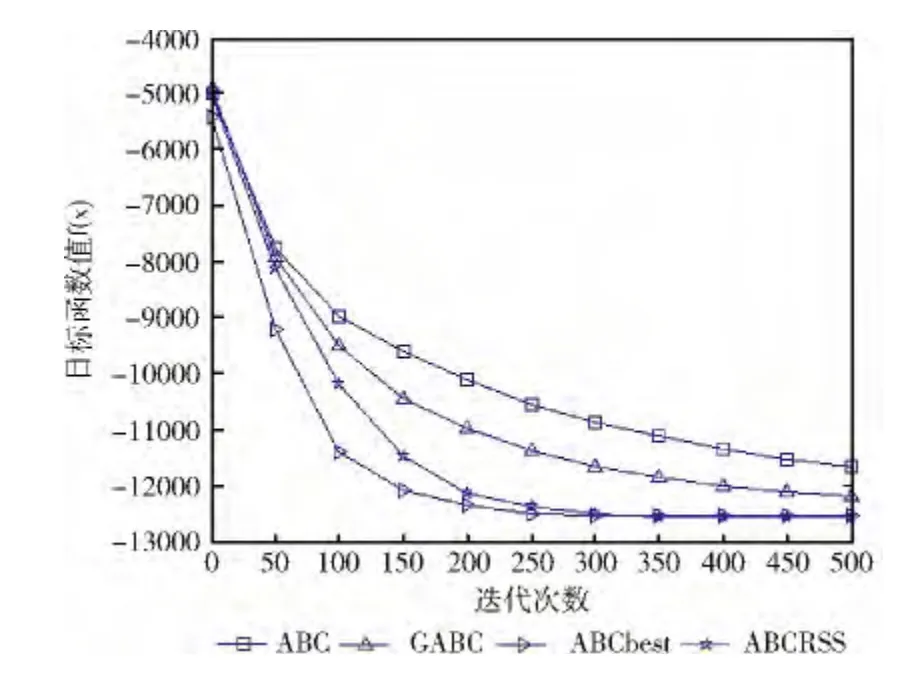
图8 Schwefel’s Problem 2.26函数收敛曲线

综上，无论是单峰函数还是多峰函数，ABCRSS 比ABC算法、GABC和ABCbest在收敛精度和收敛速度上均有较为显著的提高，并且随着函数维数的增加，ABCRSS也保持了较好的有效性和稳健性。这表明，本文提出的算法可以有效改善ABC 算法在优化高维函数时收敛速度慢、容易早熟收敛的缺陷。

4 结束语

针对人工蜂群算法容易陷入早熟的缺点，提出一种基于随机搜索策略的人工蜂群算法，该算法为提高搜索效率，在搜索过程中借鉴了差分进化算法的交叉操作，并采用随机选择的方式来进行搜索以便平衡算法的局部搜索能力和全局搜索能力，同时在搜索过程中加入一定的扰动来增强种群的多样性。8个基准测试函数的仿真实验结果表明该算法全局搜索能力好，收敛速度快，计算精度高。

［1］Karaboga D，Basturk B.On the performance of artificial bee colony（ABC）algorithm ［J］.Applied Soft Computing，2010，8 （1）：687－697.

［2］Karaboga N.A new design method based on artificial bee colony algorithm for digital IIR filters［J］.Journal of the Franklin Institute，2009，346 （4）：328－348.

［3］Singh A.An artificial bee colony algorithm for the leaf－constrained minimum spanning tree problem ［J］.Applied Soft Computing，2009，9 （2）：625－631.

［4］HU Zhonghua，ZHAO Min.Research on robot path planning based on ABC algorithm ［J］.Electric Welding Machine，2009，39 （4）：93－96 （in Chinese）.［胡中华，赵敏.基于人工蜂群算法的机器人路径规划 ［J］.电焊机，2009，39 （4）：93－96.］

［5］Alatas B.Chaotic bee colony algorithms for global numerical optimization ［J］.Expert Systems with Applications，2010，37 （8）：5682－5687.

［6］Kang F，Li JL，Ma ZY.Rosenbrock artificial bee colony algorithm for accurate global optimization of numerical functions［J］.Information Sciences，2011，181 （16）：3508－3531.

［7］Zhu GP，Kwong S.Gbest－guided artificial bee colony algorithm for numerical function optimization ［J］.Applied Mathematics and Computation，2010，217 （7）：3166－3173.

［8］BAO Li，ZENG Jianchao.A bi－group differential artificial bee colony algorithm ［J］.Control Theory ＆ Applications，2011，28 （2）：266－272 （in Chinese）.［暴励，曾建潮.一种双种群差分 蜂 群 算 法 ［J］.控 制 理 论 与 应 用，2011，28 （2）：266－272.］

［9］LUO Jun，LI Yan.Artificial bee colony algorithm with chaotic－search strategy ［J］.Control and Decision，2010，25（12）：1913－1916 （in Chinese）.［罗钧，李研.具有混沌搜索策略的蜂群优化算法 ［J］.控制与决策，2010，25 （12）：1913－1916.］

［10］GAO Weifeng，LIU Sanyang.A modified artificial bee colony algorithm ［J］.Computer ＆ Operations Research，2012，39（3）：687－697.

［11］Akay B，Karaboga D.A modified artificial bee colony algorithm for real－parameter optimization ［J］.Information Sciences，2012，192 （1）：120－142.

［12］Stron R，Price K.Differential evolution：A survey of the state－of－the art［J］.IEEE Transaction on Evolutionary Computation，2011，15 （1）：4－31.