Graph Regularized Sparse Coding Method for Highly Undersampled MRI Reconstruction
2015-12-20ZHANGMinghui张明辉YINZirui尹子瑞LUHongyang卢红阳WUJianhua吴建华LIUQiegen刘且根
ZHANG Ming-hui (张明辉),YIN Zi-rui (尹子瑞),LU Hong-yang (卢红阳),WU Jian-hua (吴建华),LIU Qie-gen (刘且根)
Department of Electronic Information Engineering,Nanchang University,Nanchang 330031,China
Introduction
Magnetic Resonance Imaging (MRI)is a crucial medical diagnostic technique which offers clinicians with significant anatomical structure for lack of ionizing.Although MRI enables highly resolution images and distinguished depiction of soft tissues, the imaging speed is limited by physical and physiological constraints.As noted in Ref.[1],increased scan duration may bring in some physiological motion artifacts.Therefore,it is necessary to decrease the acquisition time.Reducing the number of measurements mandated by Nyquist sampling theory is a way to accelerate the data acquisition at the expense of introducing aliasing artifacts in the reconstructed results.In recent years,compressed sensing (CS)theory,as a promising method, has proposed an essential theoretical foundation for data acquisition speed.Particularly, the application of CS to MRI is known as CS-MRI[2-7].
The compressed sensing has provided a crucial sparsity property that the image which has a sparse representation in certain domain can be recovered from a reduced set of measurements largely below Nyquist sampling rates[2].The traditional CS-MRI usually utilized predefined dictionaries[1,8-9],which may fail to sparsely represent the reconstructed images.By comparison, adaptive dictionary updating in CS-MRI can provide less reconstruction errors since the dictionary is learned from sampled data[10-12].For instance,Lustig[1]employed the Total Variation (TV)penalty and the wavelet transform of Daubechies for MRI reconstruction.Trzasko[6]proposed a homotopic ℓ0-minimization strategy,instead of ℓ1-minimization,to reconstruct the MR image.Recently,Ravishankar[10]assumed every image patch had sparse representation,and proposed an outstanding two-step alternating method named dictionary learning based MRI reconstruction(DLMRI).The first step is for adaptively learning the dictionary,another step is for reconstructing image from highly undersampled k-space data.Numerical experiments have indicated that these data-learning approaches obtained considerable improvements compared with previous predefined dictionaries-based methods.Nevertheless,most of existing methods fail to consider the geometrical profit information in the k-space data,which may lead to the fine details loss.
In this paper,an advanced dictionary learning method for MRI reconstruction is proposed,by employing stronger sparse prior knowledge and efficient iterative procedure.Specifically,in Ref.[13],Zheng et.al.proposed a graph regularized sparse coding method for classification.They built a k-nearest neighbor graph to encode the local structure in video data.Motivated by this idea,a comprehensive method that can better describe structure information and achieve patches discrimination for MRI reconstruction is proposed in this work.Particularly,a two-level Bregman iterative procedure is utilized.The out-level Bregman iterative enforces the data constraints, at the meantime,the inner-level is for updating dictionary and sparse representation of small overlapping image patches.Therefore,a graph regularized sparse coding method for highly undersampled MRI reconstruction (GSCMRI)is presented.Our framework considers the local geometrical structure of the image and automatically updates dictionary from under-sampled reference data.
The rest of this paper is organized as follows.The proposed formulation for MRI reconstruction based on graph regularized sparse coding is detailed in Section 1.Section 2 presents the performance of the proposed method on numerous examples under a variety of sampling schemes and undersampling ratios.Conclusion is given in Section 3.
1 Method
1.1 Reviews of the graph regularized sparse algorithm
The graph regularized sparse coding works excellently in exploiting the geometrical data by depending on manifold assumption.If two data points xi,xjare close in the intrinsic geometry of the data distribution,the coefficients of αiand αjin the new dictionary are also close to each other.Given the data X,a nearest neighbor graph G with M vertices is constructed,the each vertex represents a data point in X,and W denotes the weight matrix of G.If xiis among the k-nearest neighbors of xjor vice versa,Wij=1,otherwise,let Wij=0.Additionally,the degree of xiis defined ascM),L = C - W.Then mapping the weighted graph G to sparse representation Γ,a rational criterion for choosing a properly map is to minimize the following objective function[13]

To sum up,the objective function of graph regularized sparse coding is constructed as linear combination of the three terms:empirical loss term,Laplacian regularizer term,and L1-based sparse penalty term
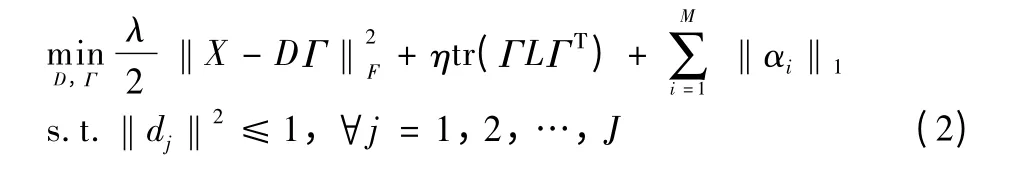
where parameter λ stands for the level of data-consistency and η determines the weight of graph regularized Laplacian regularizer term.
1.2 Propsoed GSCMRI method
Recently,Liu[11]proposed a two-level Bregman iterative method with adaptive dictionary updating[14-15](TBMDU)for highly undersampled MRI reconstruction.Generally, they employed the sparseland model J(u) =as the regularization term to solve the objective function

The Bregman iterative methodis to transform the constrained problem Eq.(3)into a sequence of unconstrained sub-problems
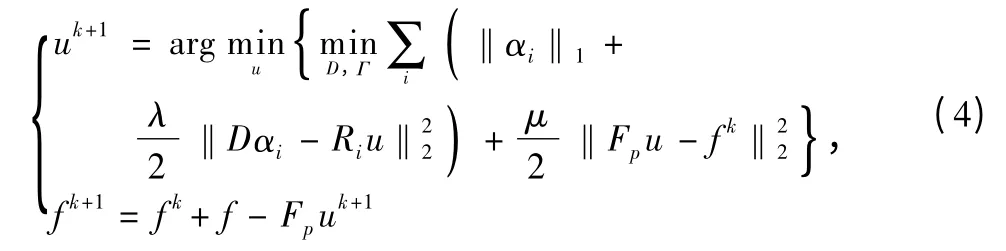
where u∈CNrepresents an image to be reconstructed,and f∈CQdenotes the undersampled Fourier measurements.The partially sampled Fourier encoding matrix Fp∈CQ×Nmaps u to f such that Fpu=f,D =[d1,d2,…,dJ]∈CM×Jand Γ= [α1,α2,…,αI]∈CJ×I.The parameter λ balances the sparse level of the image patches and the approximation error in the updating dictionary.For many natural or medical images,the value of λ can be determined empirically with robust performance in our work.J=K·M,K measures the over-completeness factor of the dictionary.
On the basis of graph regularized sparse coding and the two-level Bregman method for dictionary updating,a Graph regularized Sparse Coding algorithm for MRI reconstruction GSCMRI will be derived.The novel proposed comprehensive framework can automatically update patch-based dictionaries which learn prior information from fully sampled k-space data.Additionally, the hybrid algorithm can get promising improvements in reconstruction and the results can avoid many aliasing artifacts.The graph regularized sparse coding is combined with sparseland model,the objective function Eq.(5)can be gained as follows:

1.2.1 Dictionary updating
By utilizing splitting operator to deal with the sub-problem in Eq.(5),an equivalent unconstrained problem is gained by transforming the constrained problem as follows:

The split Bregman method/Augmented Lagrangian is used to solve problem Eq.(6),namely

where Y = [y1,y2,…,yI]∈CM×Iis the Lagrange multiplier and β is a positive constant.Z =[z1,z2,…,zI]∈CM×I.The function Eq.(7)can be minimized alternatively with respect to one variable at a time.Taking the derivative of the functionwith respect to D,it yields the following update rule
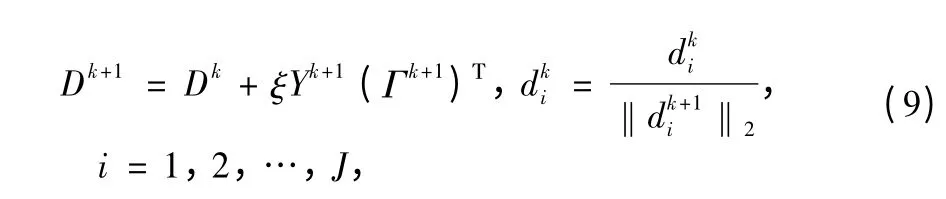
where ξ is the iterative stepsize.
1.2.2 Sparse coding

Then,substituting Z of Eq.(10)into Eq.(7),it can get

By taking advantage of the iterative shrinkage/thresholding algorithm (ISTA)[11,16],it solves the solution of αiby the following
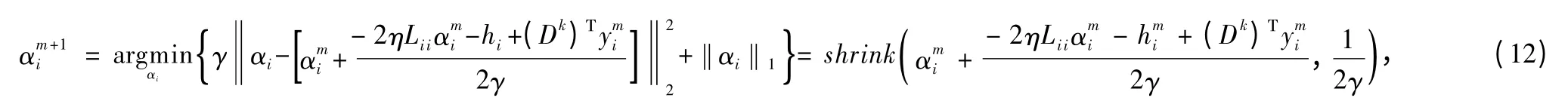

1.2.3 MR image reconstruction
Updating u by eliminating the constant variables D,Γ,and Z,we obtain the update rule by tackling with the following minimization
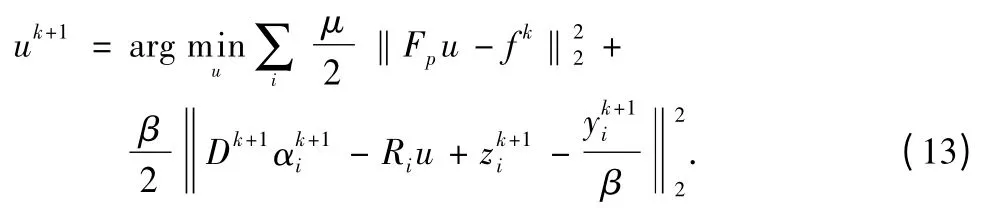
Then,the least squares solution of u is expressed as
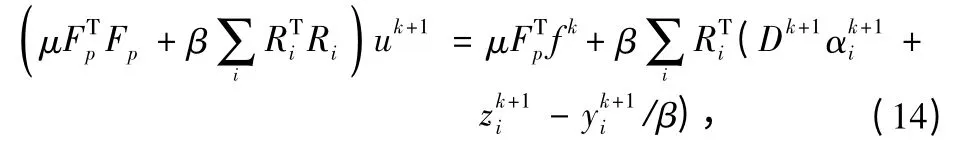
andit yields

where F ∈CN×Nrepresents the full Fourier encoding matrix,and the normalization is FΤF = 1N.Fu stands for full k - space data,and Ω denotes the subset of data which has been sampled.By averaging the patch results and transforming it into Fourier domain,it has
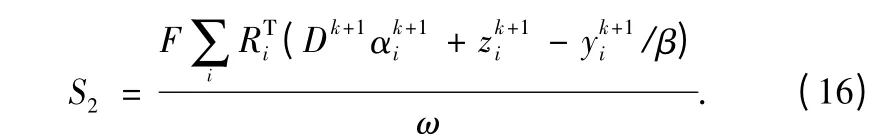
2 Experiments and Results
In this section,the performance of proposed method is evaluated under real-valued images and complex-valued data.Real-valued dictionaries are served for the simulated experiments with real-valued images,and complex-valued dictionaries are served for the actual MR data experiments.The sampling schemes employed in our experiments include the 2D random sampling[6],Cartesian sampling with random phase encodings(1D random)[1,10],and pseudo radial sampling[6,10].The images used in the real-valued experiments are in vivo MR scans of size 512 ×512 (many of which are courtesy of Ref.[17]and used in Ref.[7]).The complex-valued data[11-12,18-19]in Figs.4 and 5 are size of 256 ×256 and 512 ×512,respectively.The nominal values of the various parameters were set as the same in TBMDU method,patch size= 6,the overcompleteness of the dictionary K =1 (corresponding to J=36),the patch overlap r =1 (correspondingly J=36 and the number of data samples L =267 289 for a 512 ×512 image under the wrap around condition).For other unshared parameters,both DLMRI and TBMDU methods are set by default values.In the implementation of our method,the parameter η = 10-3was chosen by our test that will be studied in subsection 2.3.In addition,the peak signal-to-noise ratio (PSNR*)and highfrequency error norm (HFEN)[10]are introduced to quantify the quality of our reconstruction.All experiments are implemented in MATLAB 7.11 on a PC equipped Intel core i7-3632QM and 4 GByte RAM.It is worth noting that,compared with TBMDU,the mainly added computational time of the proposed method GSCMRI is the updating of Laplacian regularized matrix L at each outer-level iteration and its multiplication with coefficientsin Eq.(12)at each innerlevel iteration.Fortunately,the matrix L is a sparse matrix and hence these operations can be efficiently implemented by MATLAB.
2.1 Reconstruction of Real-valued Image
Figure 1 illustrates the reconstruction results wit h the pseudo radial sampled k-space at a range of undersampling factors with 2.5,4,6,8,10,and 20.The PSNR and HFEN values for DLMRI,TBMDU,and GSCMRI at a variety of factors are presented in Figs.1 (b)and(c).For the subjective comparison,the construction results and magnitude image of the reconstruction error produced by the three methods at 8-fold undersampling were presented in Figs.1 (d)-(f)and Figs.1(g)-(i),respectively.As can be seen from the edge boundaries in right-bottom region of Fig.1 (i),the magnitude image of the reconstruction error for GSCMRI shows less pixel errors and detail information than those of DLMRI(Fig.1 (g))and TBMDU (Fig.1 (h)).
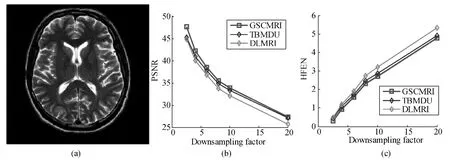
* The PSNR is defined as:PNSR=20lg 255/RMSE,where RMSE is the root mean error estimated between the ground truth and the reconstructed image.
The reconstructions at 7.11-fold undersampling are presented in Fig.2.Three different sampling schemes,namely 2D random sampling,Cartesian sampling,and the pseudo radial sampling pattern are employed respectively.The PSNR and HFEN curves are plotted in Figs.2 (b)and (c)corresponding to DLMRI,TBMDU,and GSCMRI.It can be seen that the more irrelevant the acquisition is,the better reconstruction will be gained,and therefore,the PSNRs obtained by 2D random sampling get more improvements than those of other sampling schemes.The results by applying 2D random sampling are presented in Figs.2 (d)-(f).The magnitude error image for GSCMRI shows that the reconstructed result using the proposed algorithm is more consistent than the other methods.It can be seen that although under the same undersampling rate,the improvements gained by GSCMRI outperform other methods at different trajectories.

To evaluate the sensitivity of DLMRI,TBMDU,and GSCMRI at different levels of complex white Gaussian noise,the reference image of Fig.3 (a)is applied in the three methods under 2D random sampling at 7.11-fold acceleration.Figure 3 displays the reconstruction results of three methods at different levels of complex white Gaussian noise.The PSNRs of DLMRI,TBMDU,and GSCMRI at different standard deviations (σ =2,5,8,10,14.2)are plotted in Fig.3 (c).Reconstruction results with noise σ=5 are shown in Figs.3 (d)-(f).Particularly,it should be noted that the GSCMRI reconstruction error image(Fig.3 (i))preserves less error information than those of DLMRI and TBMDU.It is revealed that our method enables to achieve more accurate reconstruction of image contrast and sharper anatomical depiction in noisy case.
2.2 Reconstruction of Complex-valued Data
For the water phantom data tested in Fig.4 (a),radial sampling trajectory with 4-fold undersampling is employed in this experiment.The reconstruction results of the three methods are shown in Figs.4 (c)-(e).The enlargements of the outputs are displayed in Figs.4 (f)and (g).As can be observed from the enlargements,the proposed method achieves the best resolution among the three reconstructions.

Fig.4 Reconstruction comparison on water phantom data ((a)is the fully sampled image;(b)is the radial sampling with 4-fold mask data;(c)-(e)are the reconstruction images corresponding to DLMRI,TBMDU,and GSCMRI;(f)and (g)are enlargements of (a)-(e))
In Fig.5,Cartesian sampling trajectory with 5-fold undersampling is employed to obtain the T2-weighted k-space data of a brain.The full-sampled reconstruction and the 5-fold undersampling mask are displayed in Fig.5 (a)and (b),respectively.The reconstructions of DLMRI,TBMDU,and GSCMRI are presented in Fig.5 (c)-(e),respectively.In order to facilitate the observation,the difference image between reconstruction results of the full-sampling and 5-fold undersampling are shown in Figs.5 (f)-(h).It can be seen from the right-bottom regions of the error image that GSCMRI provides smaller magnitude values.

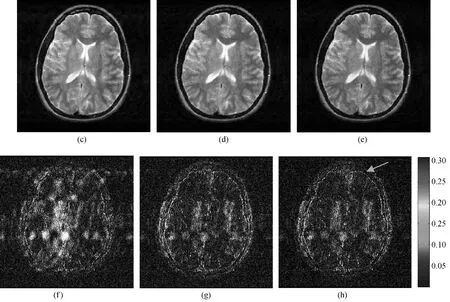
Fig.5 Reconstruction comparison on T2-weighted k-space data ((a)is the fully sampled image;(b)is cartesian sampling with 5-fold mask data;(c)-(e)are reconstructed images using DLMRI,TBMDU,and GSCMRI;(f)-(h)are the relative difference images)
2.3 Parameter Choices of η
The proposed algorithm GSCMRI introduces the new parameter η which determines the weight of Laplacian regularizer term.In previous experiments,the value of η is empirically set to be η = 10-3.In this subsection,the performances of different values η = (10-1,10-2,10-3,10-4,10-5)are investigated in Fig.6.The PSNR and HFEN versus η are presented in Figs.6 (b)and (c),where the PSNR achieves the highest and HFEN achieves the lowest at the point η = 10-3,indicating that the choice of η= 10-3can achieve promising result than other values of η.Specifically,the reconstruction results and magnitude images of reconstruction error in the case of η = 10-1,10-3,10-5are shown in Figs.6 (d)-(f)and Figs.6(g)-(i),respectively.The error magnitude images have shown that the case of η =10-3has smaller magnitude error than those in η =10-1and η=10-5.Therefore,the case of η=10-3is a wonderful choice for the experiments.


Fig.6 The performances of varying η((a)is the reference image;(b)and (c)are PSNR and HFEN versus η;(d)-(f)are the reconstructions of η=10 -1,η=10 -3,and η=10 -5;(g)-(i)are the reconstruction errors of (d)-(f))
3 Conclusions
In this work,a GSCMRI is proposed.The novel sparse representation explicitly considers the manifold structure of the k-space data,and the adaptive patch-based dictionary updating is employed to specific image instance.Consequently,our graph regularized sparse coding method for MRI reconstruction can efficiently capture local image structures and adaptive dictionary updating can sparsify images better than preconstructed dictionary.Various experimental results demonstrate the superior performance of the method under real-valued image and complex-valued data.The proposed method has highly accurate reconstructions for severely undersampled factors,and significantly improvements in both noiseless and noisy cases.The presented framework can be partially extended to parallel imaging applications in the future work.Besides,replacing ISTA by fast iterative shrinkage/thresholding algorithm(FISTA)[20]to improve the reconstruction speed will be investigated in the forthcoming study.
[1]Lustig M,Donoho D,Pauly J M.Sparse MRI:The Application of Compressed Sensing for Rapid MR Imaging [J].Magnetic Resonance in Medicine,2007,58(6):1182-1195.
[2]Donoho D.Compressed Sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[3]Caballero J,Price A,Rueckert D,et al.Dictionary Learning and Time Sparsity for Dynamic MR Data Reconstruction[J].IEEE Transactions on Medical Imaging,2014,33(4):979-994.
[4]Lustig M,Donoho D,Pauly J M.k-t SPARSE:High Frame Rate Dynamic MRI Exploiting Spatio-Temporal Sparsity [C].Proceedings of 13th International Society for Magnetic Resonance in Medicine,Seattle,USA,2006.14(1):2420.
[5]Lingala S,Jacob M.Blind Compressive Sensing Dynamic MRI[J].Medical Imaging,IEEE Transactions on Medical Imaging,2013,32(6):1132-1145.
[6 ]Trzasko J, Manduca A.Highly Undersampled Magnetic Resonance Image Reconstruction via Homotopic l0Minimization[J].IEEE Transactions on Medical Imaging,2009,28(1):106-121.
[7]Wang Y,Ying L.Compressed Sensing Dynamic Cardiac Cine MRI Using Learned Spatiotemporal Dictionary [J].IEEE Transactions on Biomedical Engineering,2014,61(4):1109-1120.
[8]Guerquin-Kern M,Haeberlin M,Pruessmann K,et al.A Fast Wavelet-Based Reconstruction Method for Magnetic Resonance Imaging[J].IEEE Transactions on Medical Imaging,2011,30(9):1649-1660.
[9]Dibella E V R,Chen L,Schabel M.Reconstruction of Dynamic Contrast Enhanced Magnetic Resonance Imaging of the Breast with Temporal Constraints[J].Magnetic Resonance Imaging,2010,28(5):637-645.
[10]Ravishankar S,Bresler Y.MR Image Reconstruction from Highly Undersampled k-space Data by Dictionary Learning [J].IEEE Transactions on Medical Imaging,2011,30(5):1028-1041.
[11]Liu Q G,Wang S S,Yang K,et al.Highly Undersampled Magnetic Resonance Imaging Reconstruction Using Two-Level Bregman Method with Dictionary Updating [J].IEEE Transactions on Medical Imaging,2013,32(7):1290-1301.
[12]Qu X B,Guo D,Ning B D,et al.Undersampled MRI Reconstruction with Patch-Based Directional Wavelets [J].Magnetic Resonance Imaging,2012,30(7):964-977.
[13]Zheng M,Bu J J,Chen C,et al.Graph Regularized Sparse Coding for Image Representation [J].IEEE Transactions on Image Process,2011,20(5):1327-1336.
[14]Liu Q G,Wang S S,Luo J H.A Novel Predual Dictionary Learning Algorithm[J].Journal of Visual Communication Image Represention,2012,23(1):182-193.
[15]Liu Q G,Luo J H,Wang S S,et al.An Augmented Lagrangian Multi-scale Dictionary Learning Algorithm [J].EURASIP Journal on Advances in Signal Processing,2011,2011(1):1-16.
[16]Yin W,Osher S,Goldfarb D,et al.Bregman Iterative Algorithms for ℓ1-Minimization with Applications to Compressed Sensing[J].SIAM Journal on Imaging Sciences,2008,1(1):143-168.
[17]American Radiology Services.[DB/OL].(2009)[2014].http://www3.americanradiology.com/pls/web1/wwmain.home,2014.
[18]Ning B D,Qu X B,Guo D,et al.Magnetic Resonance Image Reconstruction Using Trained Geometric Directions in 2D Redundant Wavelets Domain and Non-convex Optimization[J].Magnetic Resonance Imaging,2013,31(9):1611-1622.
[19]Qu X B,Hou Y K,Lam F,et al.Magnetic Resonance Image Reconstruction from Undersampled Measurements Using a Patch-Based Nonlocal Operator[J].Medical Image Analysis,2014,18(6):843-856.
[20]Beck A,Teboulle M.A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems [J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.
杂志排行
Journal of Donghua University(English Edition)的其它文章
- Group Performance Evaluation in Universities with Entropy Method
- Synthesis and Application of Polyurethane Modified Organic Silicone Wet Rubbing Fastness Improver
- Inactivation of Giardia Intestinalis by Peroxone Process (H2 O2 /O3)and Its Disinfection Mechanisms
- Optical Measurements to Reveal Roles of Slightly Crosslinked Poly(dimethyldiallylammonium chloride)s in Fixing Anionic Dyes on Cotton Fabric
- Portfolio Choice under the Mean-Variance Model with Parameter Uncertainty
- Behavior of Benzene Decomposition by Using Pulse Modulated Power Supply
