基于动态贝叶斯网的航班延误传递分析
2015-12-20丁建立赵键涛曹卫东胡海生
丁建立,赵键涛+,曹卫东,胡海生,黄 威
(1.中国民航大学 计算机科学与技术学院,天津300300;2.中国民航信息网络股份有限公司,北京100010)
0 引 言
航班链中的各个航班发生延误受到的影响因素是多方面的,对于单个航班在知道上游航班延误的情况下,很难对下游航班进行预测。然而,可以针对大多数航班链中的延误传递情况进行分析,从中发现多数情况下延误传递的普遍规律,这无疑也具有重要现实意义。
在国外,学者针对航班延误,从不同角度进行了研究。Pyrgiotis等用排队论的思想建立了一个机场网络模型对航班延误进行研究,指出了在机场网络模型中考虑延误传播的重要性[1];Barnhart等针对乘客到达延误,采用了一种自适应的启发式方法来估计旅客到达延误的影响,同时研究了影响航空系统正常运行的主要因素[2];Hao等研究了某几个机场的延误给整个机场网络带来影响,得出部分机场的延误状况不能够对整个航空系统的延误状况进行估计的结论[3];AhmadBeygi等研究了航班计划与航班延误的关系,指出了在当前状况下即使航班计划预留出松弛时间用于吸收延误,在上游的航班发生延误的条件下,延误依然会向下游航班传播[4],但是可以采取增加航班在机场的周转时间的方式来减少延误向下游机场的传递[5];Song等从机场容量的角度出发,研究了天气对机场容量的影响[6];Laskey等用静态贝叶斯网对各种影响因素及航班延误之间的关系进行了建模[7],但是没有考虑到飞机在机场周转时间等因素。
在国内,应圣钢等运用优化方法,研究了如何对飞机进行合理化调度,以减小潜在损失[8,9],但没有涉及如何进行预测;丁建立、徐涛等采用生物免疫、支持向量机、马尔科夫链等方法对机场航班延误数量进行预测[10-13],但没有涉及航班链中延误的传播性。曹卫东、刘玉洁等用静态贝叶斯网络的方法对航班延误传播进行了分析,但没有考虑到计划过站时间的因素及网络参数学习问题[13,14]。
本文针对航班延误传递的特点,采用动态贝叶斯网对航班链上的航班延误传递状况进行分析,研究了过站时间对延误传播的影响,并对延误传递过程中延误时间的不确定性进行了度量,比较了延误传递各个过程中的不确定大小。
1 航班延误传递模型
航空公司为了提高飞机利用率,通常会安排一架飞机在一天之内执行多个航班,当上游航班发生延误时,延误有可能会向下游传播。若一个航班链中有p 个航班,每个航班离港延误时间为Ti,i=1,2,…,p,则下一航班离港延误时间与上一航班离港延误时间有关系,而与上一航班之前的航班离港延误时间没有关系,具有一阶马尔可夫性。离港延误时间的传递关系如图1所示。

图1 航班延误传递
将延误时间离散化,设ti表示延误时间为第i 个状态,第p 个航班离港延误时间为ti的概率为P(Tp=ti),运用消元法
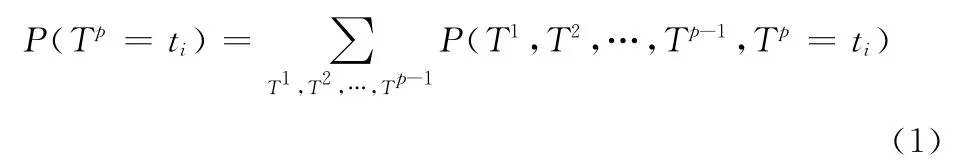
由于下一段航班离港延误时间与上一段航班有关系,具有马尔可夫性,所以
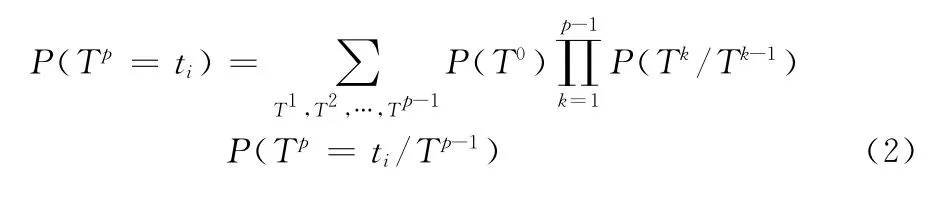
而这个关系正好可以用动态贝叶斯网来表达。
2 航班延误传递的动态贝叶斯网络
动态贝叶斯网络以概率论为基础,是一种把静态贝叶斯网络与时间信息结合,能够表达时序数据的随机模型。动态贝叶斯网络的可以看成是随机过程的图形模式[16]。
动态贝叶斯网(DBN)可以定义为(B0,B→),其中B0是先验网络,定义在初始状态上的联合概率分布,B→是转移网。设X[t]表示t时刻随机变量的取值,定义转移概率P(X[t+1]/X[t])。在时刻1,X[1]中的父节点是在先验网络B0中的节点,在时刻t+1,X[t+1]的父节点是那些在t时刻和t+1中都相关的在B→中的节点。动态贝叶斯网假设动态概率过程是马氏的,即
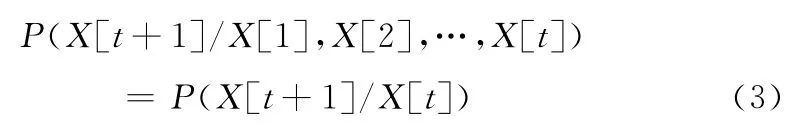
也就是说t+1时刻的取值情况只与t时刻的取值情况有关,而与t时刻之前的取值情况无关。若相邻时间的条件概率过程是平稳的,那么P(X[t+1]/X[t])与时间t无关。对于一个DBN 模型,在X[0],X[0],…,X[t]上的联合概率分布为
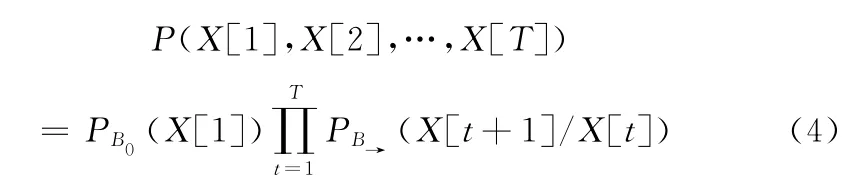
针对航班离港延误传递,对离港延误时间有影响的因素除了有上一航班的离港延误时间外,还有飞机在下一机场的计划过站时间。在上一航班离港延误时间确定的条件下,飞机在下一机场计划过站时间越长,相当于缓冲时间越多,下一航班离港延误的可能性就越小。因此,航班延误传递可以表示为在一个时间片中包含两个节点的动态贝叶斯网络,其中一个节点表示计划过站时间,另外一个节点表示离港延误时间。航班延误传递的动态贝叶斯网络如图2所示。静态贝叶斯网是一个有向无环图,弧的方向代表因果指向,而在动态贝叶斯网中为了表示的方便,允许环存在。但是,存在的环不仅代表因果关系,还意味着代表的因果关系能进行时间上的扩展。例如把图2代表的动态贝叶斯网进行扩展,扩展时间片为4,展开形式如图3所示。
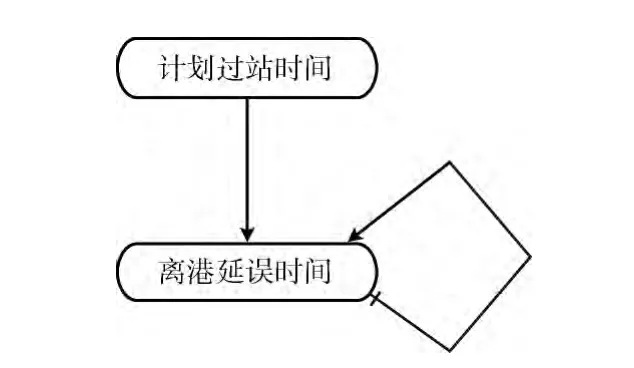
图2 航班延误传递的动态贝叶斯网络
3 航班延误传递动态贝叶斯网络参数学习
动态贝叶斯网络学习包括了结构学习与参数学习。在对航班延误传递进行研究时,采用的是采取经验确定动态贝叶斯网结构,然后再根据确定了的结构学习参数的方法。EM 方法和梯度方法是动态贝叶斯网在不完整数据集上学习参数的两种方法。

图3 包含4个时间片的动态贝叶斯网络
3.1 EM 方法
在完整数据集中用统计方法对参数进行估计时,每个样本的权重为1。而在运用含有缺失数据的数据集对参数进行学习时,EM 方法基于当前参数对缺失数据集进行修补。一个缺值样本经过修补之后权重不再是1,而是对每一种修补情况都附加一个权重。在进行数据修补后,计算当前样本集的最大似然参数估计,然后基于新的参数估计值计算似然函数值。若似然函数值增大,则基于新的参数估计值重新修补缺失数据,否则以当前参数值作为最终的参数估计值。
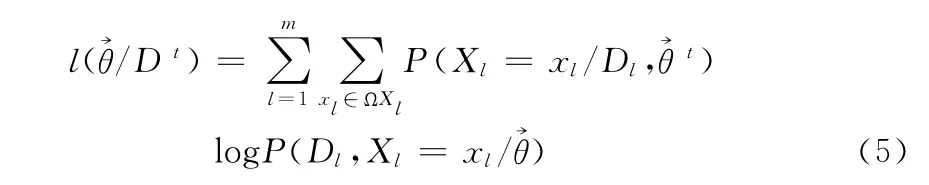
其中,P(Xl=xl/Dl,)为以Xl=xl方式修补样本的权重。当Xl= 时,样本是完整的,P(Xl=xl/Dl)=1。当对数似然函数取得最大值时
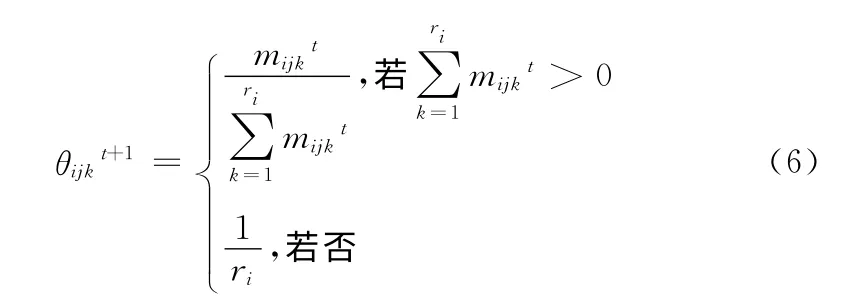
以此作为下一次迭代的参数,其中,mtijk是修补后数据Dt中所有满足Xi=k,π(Xi)=j的样本权重之和,ri为节点Xi的取值个数
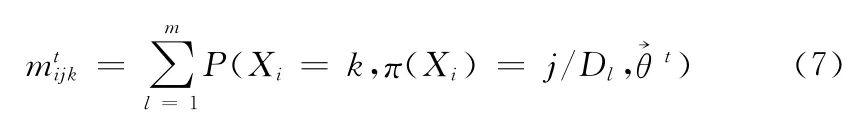
EM 算法步骤见表1。
3.2 梯度方法
同神经网络使用梯度下降的方式寻找节点间连接权重的方法类似,动态贝叶斯网参数估计选择也可以采用梯度优化的方法来寻找参数。与神经网络以误差最小化作为优化准则不同,贝叶斯网以似然函数最大化作为优化准则。神经网络中经过迭代之后收敛到误差曲面的一个局部最小值,而贝叶斯网络中经过迭代之后将收敛到似然函数曲面的一个局部最大值。给定D =(D1,D2,…,Dm)为一组独立同分布数据集,给定动态贝叶斯网结构,参数的对数似然为

表1 EM 算法步骤
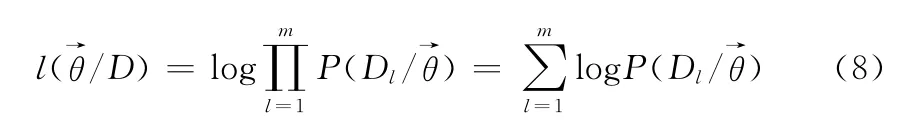
对参数求偏导
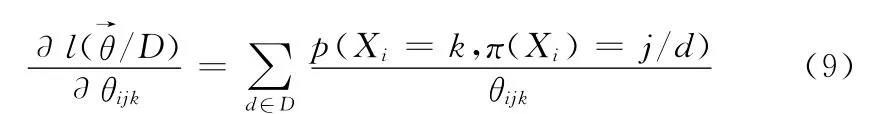
用梯度上升来更新每一个θijk,即
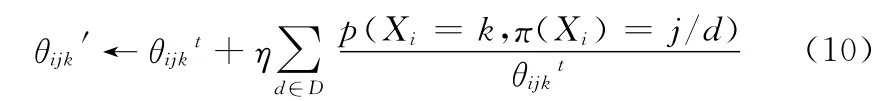
其中,η是学习率。然后再将θijk′归一化
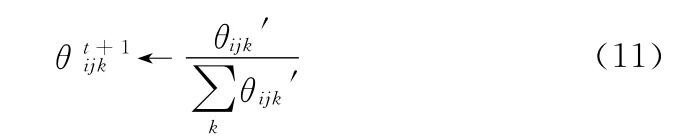
计算似然当前参数下的似然函数值,若似然函数值变大,则更新参数值,否则不更新。这样经过迭代之后,将得到参数的一个局部最大似然假设。
梯度法步骤见表2。

表2 梯度法步骤
3.3 参数学习比较
下面对两种参数学习方法进行比较,用其中比较好的方法作为航班延误传递分析动态贝叶斯网的参数学习方法,其中梯度法η设置为0.02。实验中采用的数据是国内某大型航空公司在某省的航班数据。数据预处理后共有3800条数据。图4所示为两种方法的学习曲线。
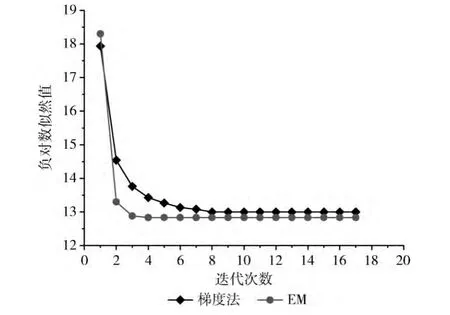
图4 航班延误传递动态贝叶斯网络参数学习曲线
似然度越大,即负的对数似然值越小,说明得到的参数越符合训练数据。从图4 中可以看到,在计算参数时,EM 方法在收敛速度和对样本数据的拟合能力上,均比梯度方法效果好。
4 基于动态贝叶斯网EM 参数学习方法的航班延误传递分析
首次航班的计划过站时间为首发计划起飞时间减去上一天最后一个航班的计划降落时间,由于首次航班的延误时间不考虑过站时间的影响,因此在展开后的动态贝叶斯网中去掉了指向首次航班离港时间的过站时间节点。训练后结果如图5所示。
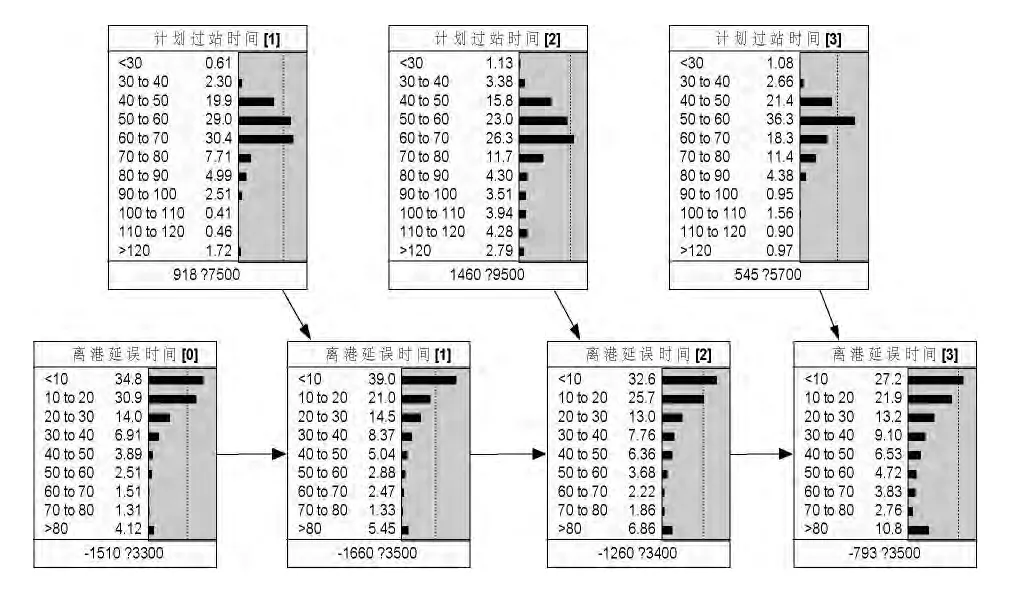
图5 基于EM 参数学习方法的航班延误传递学习结果
表3和表4为部分情况下的转移概率。对比两个表可以发现,相同条件下的转移概率并不相等,其它条件下也有类似的情况,说明航班延误传递是一个非稳态过程。
在航班实际执行之前,航班计划是已知的,所以飞机在各个机场的计划过站时间也是已知的。因此,在上游航班延误状况已知的前提下,根据动态贝叶斯网学习结果,可以得出后续航班的离港延误时间的概率分布。图6所示为首发航班时延误时间为30~40分钟,后续航班的计划过站时间都为40~50分钟时,后续航班离港延误时间的概率分布。图7所示为首发航班时延误时间为30~40分钟,后续航班的计划过站时间都为70~80分钟时,后续航班离港延误时间的概率分布。

表3 离港延误时间 [1]转移概率

表4 离港延误时间 [2]转移概率
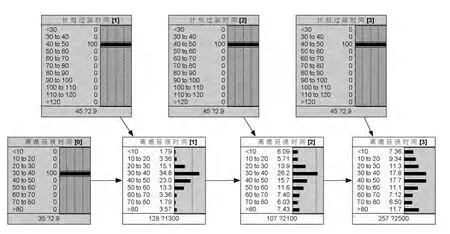
图6 航班离港延误时间概率分布1
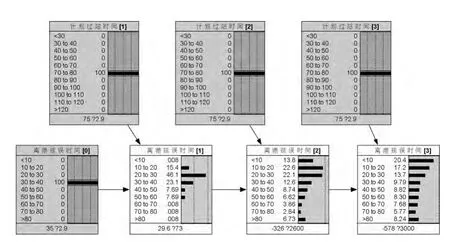
图7 航班离港延误时间概率分布2
对比图6和图7可以看到,当上游航班发生离港延误时,若下游航班过站时间充分,大多数情况下延误是可以被逐渐吸收的。其它条件下也有类似的情况。为了度量各时间片中离港延误时间的不确定性,计算各离港延误时间的熵值,熵的定义如下
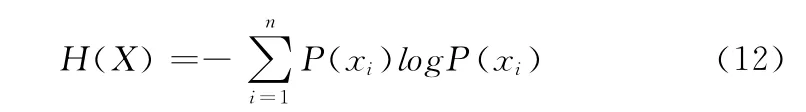
式中:P(xi)——状态xi出现的概率,n——状态个数。以变量X1,X2,X3分别代表各个时间片中的离港延误时间,按10分钟为一个状态,由公式计算上述两种不同条件下各时间片中离港延误时间的熵值,结果见表5。
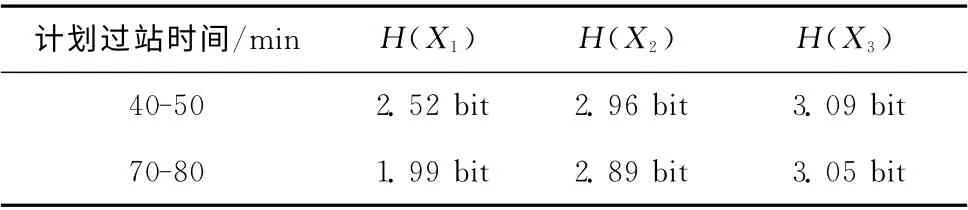
表5 不同情况下离港延误时间熵值
分析数据可以看出,上述两种情况下,在航班离港延误时间传递的过程中,随着时间片的递增,离港延误时间的熵是在不断增大的,即不确定性是在逐渐增大的,预测准确的可能性是在逐渐降低的。在其它条件下也有类似的情况。
5 结束语
本文用动态贝叶斯网对航班延误传递进行研究,并对典型的动态贝叶斯网参数学习的效果进行了比较,对其中较好的学习结果进行了分析。分析结果表明,若过站时间充分,在大部分情况下,航班延误在传递的过程中是可以被逐段吸收的。另外,随着航班延误动态贝叶斯网时间片的增加,离港延误时间的不确定性逐渐增大的,预测准确的可能性是逐渐减小的。
[1]Pyrgiotis N,Malone K M,Odoni A.Modelling delay propagation within an airport network [J].Transportation Research Part C:Emerging Technologies,2013,27:60-75.
[2]Barnhart C,Fearing D,Vaze V.Modeling passenger travel and delays in the national air transportation system [J].Operations Research,2014,62 (3):580-601.
[3]Hao L,Hansen M,Zhang Y,et al.New York,New York:Two ways of estimating the delay impact of New York airports[J].Transportation Research Part E:Logistics and Transportation Review,2014,70:245-260.
[4]AhmadBeygi S,Cohn A,Guan Y,et al.Analysis of the potential for delay propagation in passenger airline networks[J].Journal of Air Transport Management,2008,14 (5):221-236.
[5]Ahmadbeygi S,Cohn A,Lapp M.Decreasing airline delay propagation by re-allocating scheduled slack [J].IIE Transactions,2010,42 (7):478-489.
[6]Lixia S,Craig W,Daniel G,et al.Methodologies for estimating the impact of severe weather on airspace capacity [C]//The 26th Congress of International Council of the Aeronautical Sciences,2008:1-8.
[7]Laskey K B,Xu N,Chen C H.Propagation of delays in the national airspace system [C]//Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence,2012.
[8]YING Shenggang,SUN Fuchun,HU Laihong,et al.Multiobjective dynamic programming algorithm for aircraft arrival sequencing and runway scheduling [J].Control Theory &Applications,2010,27 (7):827-835 (in Chinese). [应圣钢,孙富春,胡来红,等.基于多目标动态规划的多跑道进港排序[J].控制理论与应用,2010,27 (7):827-835.]
[9]LI Xiaolan,LE Meilong.Heuristic algorithm in stages of multi-objective aircraft and passenger recovery [J].Application Research of Computers,2014,31 (8):2270-2274 (in Chinese).[李晓岚,乐美龙.多目标飞机和旅客恢复分阶段启发式算法 [J].计算机应用研究,2014,31 (8):2270-2274.]
[10]DING Jianli,YANG Haitong,GU Bin.Adaptive real-time forecasting method of airdrome flight delay based on fuzzy immunization strategy [J].Journal of Nanjing University of Aeronautics & Astronautics,2011,43 (2):257-261 (in Chinese).[丁建立,杨海彤,顾彬.基于模糊免疫策略的机场航班延误自适应实时预测方法 [J].南京航空航天大学学报,2011,43 (2):257-261.]
[11]DING Jianli,TONG Guansheng,XU Tao.Detecting and implementing of airport scheduled flight delay state base on immune negative selection algorithm [J].Chinese High Technology Letters,2008,18 (4):387-391 (in Chinese). [丁建立,仝冠生,徐涛.基于免疫否定选择算法的机场航班延误状态检测与实现[J].高技术通讯,2008,18 (4):387-391.]
[12]XU Tao,DING Jianli,GU Bin,et al.Forecast warning level of flight delays based on incremental ranking support vector machine [J].Acta Aeronautica Et Astronautica Sinica,2009,30 (7):1256-1263 (in Chinese). [徐涛,丁建立,顾彬,等.基于增量式排列支持向量机的机场航班延误预警[J].航空学报,2009,30 (7):1256-1263.]
[13]LV Xiaojie,WANG Hong.Method for swept flight delay early warning of large aeronautic hub [J].Computer Engineering and Design,2011,32 (8):2829-2832 (in Chinese).[吕晓杰,王红.大型枢纽机场大面积航班延误预警方法研究 [J].计算机工程与设计,2011,32 (8):2829-2832.]
[14]CAO Weidong,HE Guoguang.Bayesian networks analysis for sequence flight delay and propagation [J].Journal of Computer Applications.2009,29 (2):606-610 (in Chinese).[曹卫东,贺国光.连续航班延误与波及的贝叶斯网络分析 [J].计算机应用,2009,29 (2):606-610.]
[15]LIU Yujie.Flight delay transmit forecast based on Bayesian network [D].Tianjin:Tientsin University,2009 (in Chinese). [刘玉洁.基于贝叶斯网络的航班延误与波及预测[D].天津:天津大学,2009.]
[16]REN Jia,GAO Xiaoguang.Bayesian network parameter learning and decision support for UAVs [M].Beijing:National Defence Industry Publisher,2012:70-100 (in Chinese).[任佳,高晓光.贝叶斯网络参数学习及对无人机的决策支持 [M].北京:国防工业出版社,2012:70-100.]
