基于模糊局部二值模式算子的图像伪造检测

张智丰，裴志利

（内蒙古民族大学 计算机科学与技术学院，内蒙古 通辽028000）

0 引 言

为了确保图像信息的真实性［1－3］，研究人员提出了相应的图像伪造检测算法。其中，以移动复制伪造检测研究最为广泛。MF HashmiI等［4］为了提高算法检测精度，提出了DWT 耦合SIFT 变换的图像伪造检测算法，实验结果显示其算法具有良好的检测精度。然而，SIFT 变换是提取图像特殊点的关键点，难以有效检测模糊、旋转等篡改。为了克SIFT 变换的弊端，Amerini等［5］提出了基于J－Linkage算法的鲁棒聚类均值的复制移动伪造检测算法，仿真结果表明该算法的鲁棒性得到了进一步地提高，但是，J－Linkage算法无法消除图像特征的误配现象。王任华等［6］利用RANSAC去除误配区域，得到模型参数，精确定位伪造区域，仿真结果显示其将RANSAC用于图像伪造检测，能够有效降低特征误配率，提高算法的检测精度，但是，RANSAC策略仍然需要设置阈值，其检测精度仍然受阈值的影响，且难以有效检测缩放等伪造区域。

尽管当前图像复制移动伪造检测算法能够对图像进行真伪决策，可识别出伪造区域，但是此类算法都需要提前设置阈值参数，自适应较差，且难以兼顾高的检测精度与鲁棒性。

近年来，局部二值模式LBP （local binary patterns）［7］已被学者用于决策图像真伪，能有效检测旋转、亮度变化等伪造区域，但是其检测精度不佳，难以识别噪声、缩放等伪造区域，且难以去除图像特征误配点对问题。文献［6，7］为图像伪造检测提供了一个新思路。对此，本文引入模糊集理论，联合传统的LBP，设计了模糊二值模式算子，增强算子的识别能力，嵌入随机样本一致策略，消除图像特征误配，提出了随机样本一致策略耦合模糊二值模式算子的图像伪造检测算法。最后，在Matlab平台上测试了本文算法的检测精度与鲁棒性能。

1 本文图像伪造检测算法设计

本文算法流程如图1所示。从图中可知，本文算法主要含有：①基于模糊局部二值模式算子的图像特征提取；②设计新的块匹配算法，完成特征匹配；③基于随机样本一致算法的特征误配消除，精确检测出伪造区域。

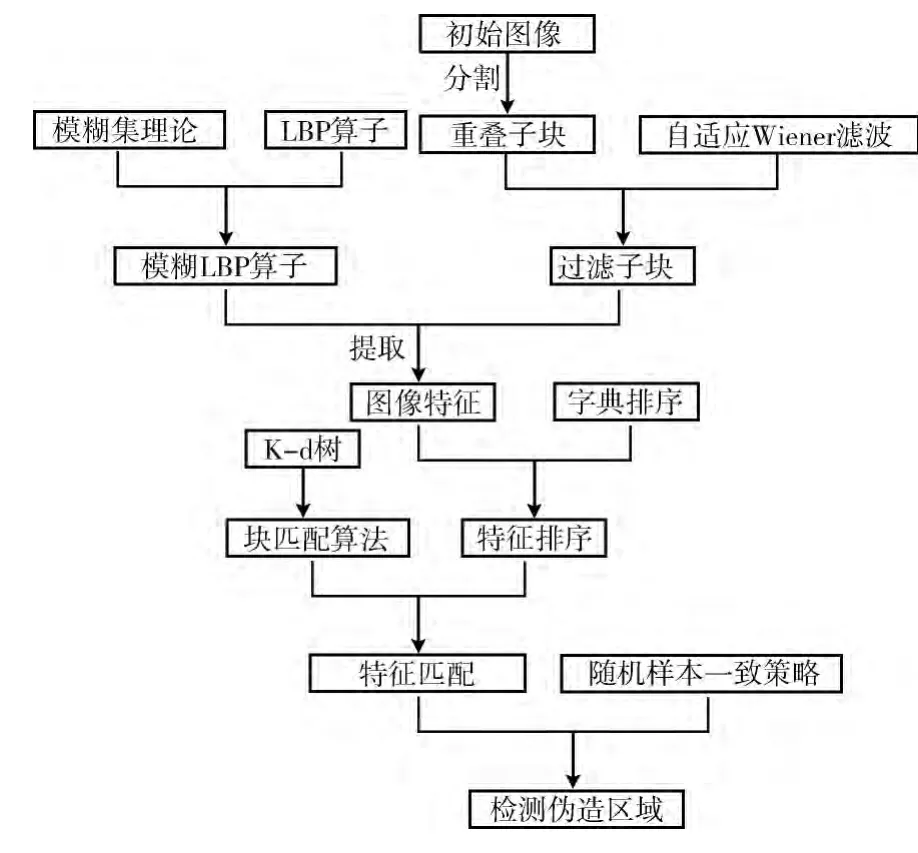
图1 本文算法流程

1.1 模糊局部二值模式算子的设计及特征提取

假设图像I的尺寸为M×N，将其分割成尺寸为B×B的重叠子块b1，b2，…，bTB；且这些子块的尺寸要小于待检测的伪造区域的尺寸。依据如下模型确定重叠子块的数量

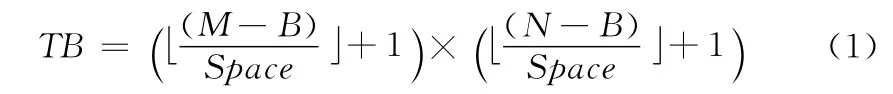
再引入自适应Wiener 滤波［8］，过滤这些重叠子块

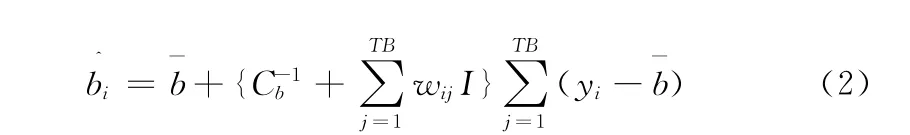
经过Wiener滤波处理后，能够较好地保持图像边缘与图像高频成分；随后设计模糊局部二值模式算子FLBP（fuzzy local binary pattern），提取图像特征。

对于图像中的每个像素，传统的局部二值模式算子LBP只考虑一个3×3的窗口；并以矩形中心点的灰度值为阈值，对矩形内其它像素作二值化处理，然后根据像素的不同位置进行加权求和得到该窗口的LBP 值［9］。图1显示了传统LBP算子的计算过程。给定中心像素，则LBP值可以通过与其领域像素的比较，来计算

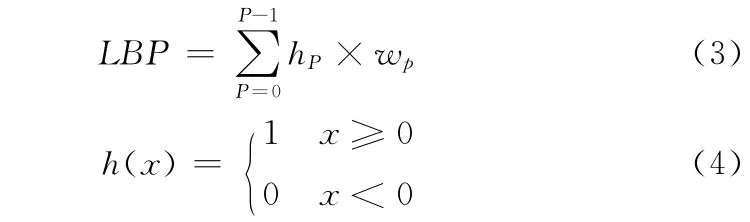
其中，P 为领域像素数量；wp＝2P为权重；hp＝（dn－dc）代表局部中心像素与领域像素的灰度差值。

传统LBP算子的计算如图2所示。

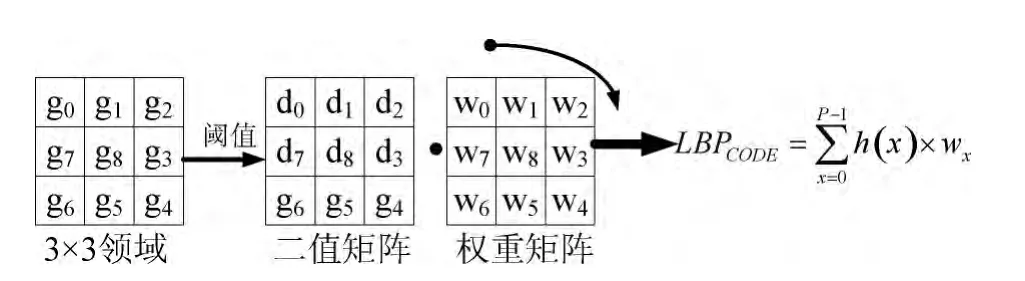
图2 传统LBP算子的计算

为了改善LBP算子只能局限于方形的不足，Ojala等［9］对其进行拓展，通过不断旋转圆形邻域得到一系列初始定义的LBP值，取其最小值作为该邻域的LBP值，如图3所示。LBP值计算模型为

式中：R——圆形半径；ROR ——旋转函数。

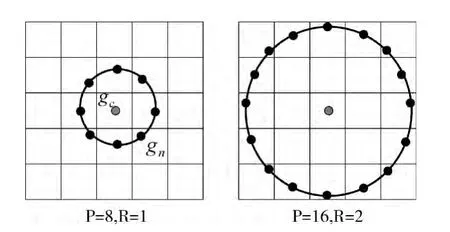
图3 不用P与R 的圆形对称领域

可见，不管是传统的LBP算子，还是拓展后的LBP算子，其通过周边像素的硬阈值，来提取特征，使其对噪声、相差较小的像素非常敏感，在面对大范围的相似区域时，LBP算子的识别能力较弱，难以去除图像特征误配点对问题。

故本文引入模糊逻辑，联合模型 （1），设计了模糊二值模式算子，将局部领域分割成更多的二值模式，以增强算子的描述能力，使其能感知图像灰度水平的不确定性，有效检测噪声。给定数字图像，假设B 为区间［greference，gmax］内所有像素Px的模糊集合；S为区间［0，greference］内所有像素Px的模糊集合。其中，gmax为领域像素的最大灰度；greference为参考灰度。则B、S 模型为

其中，uB、uS分别为模糊集合B 、S 的隶属度函数，代表着每个像素属于闭区间［0，1］的程度；H ＝｛0，1，2…n－1｝为n个领域像素数量。

隶属度函数uB、uS的定义如下

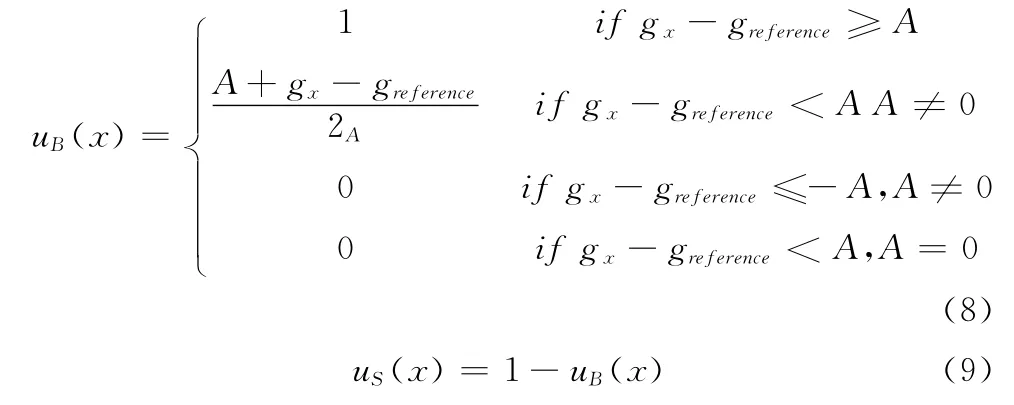
其中，A ∈［0，gmax］代表控制模糊度的参数；

可见，模糊局部二值模式算子可以用多个LBP 编码表示，其结构如图4所示。那么模糊LBP 算子的n个像素的领域可以用多个有序对 （LBP 编码，CLBP值）来表示。其中，CLBP代表LBP编码对其直方图的贡献度，根据隶属度函数uB、uS，则CLBP计算模型如下

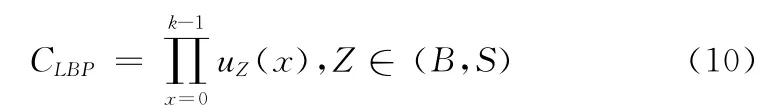
其中，k∈（0，n）代表参与LBP编码计算的领域像素数量。

依据模型 （8），对于一个外围像素，由于不同的贡献值，会产生不同的LBP编码。则对于一个含有n个像素的领域，对直方图的总贡献CTotal为

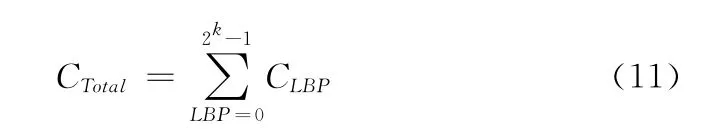
对于尺寸为M×N 的图像，通过确定每个像素（i，j）的FLBP模式后，再计算整个图像的FLBP 编码的归一化直方图，以此作为特征矢量

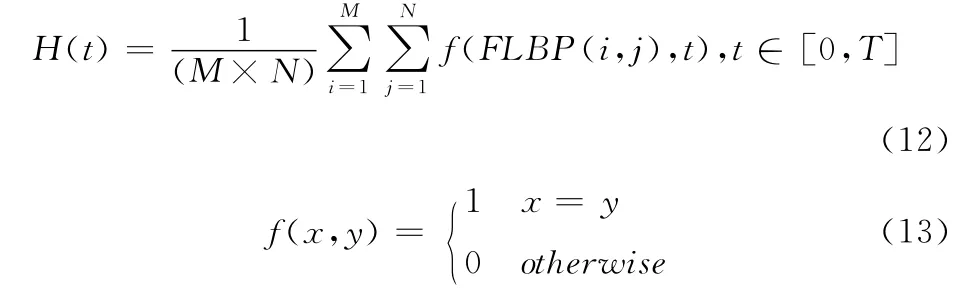
以尺寸为128×128的图像为例，分割成10×10大小的重叠块，取3个贡献值CLBP＝0.2，0.5，1，则会产生3个FLBP 算子。对于第n 个图像分块，依据模糊LBP 算子，会产生3个特征矢 量V1，n，V2，n，V3，n；为 了 消 除 光 照 变换影响，引入归一化技术［10］，将特征矢量V1，n，V2，n，V3，n内的所有元素值置于区间［0，1］内，如图5所示。

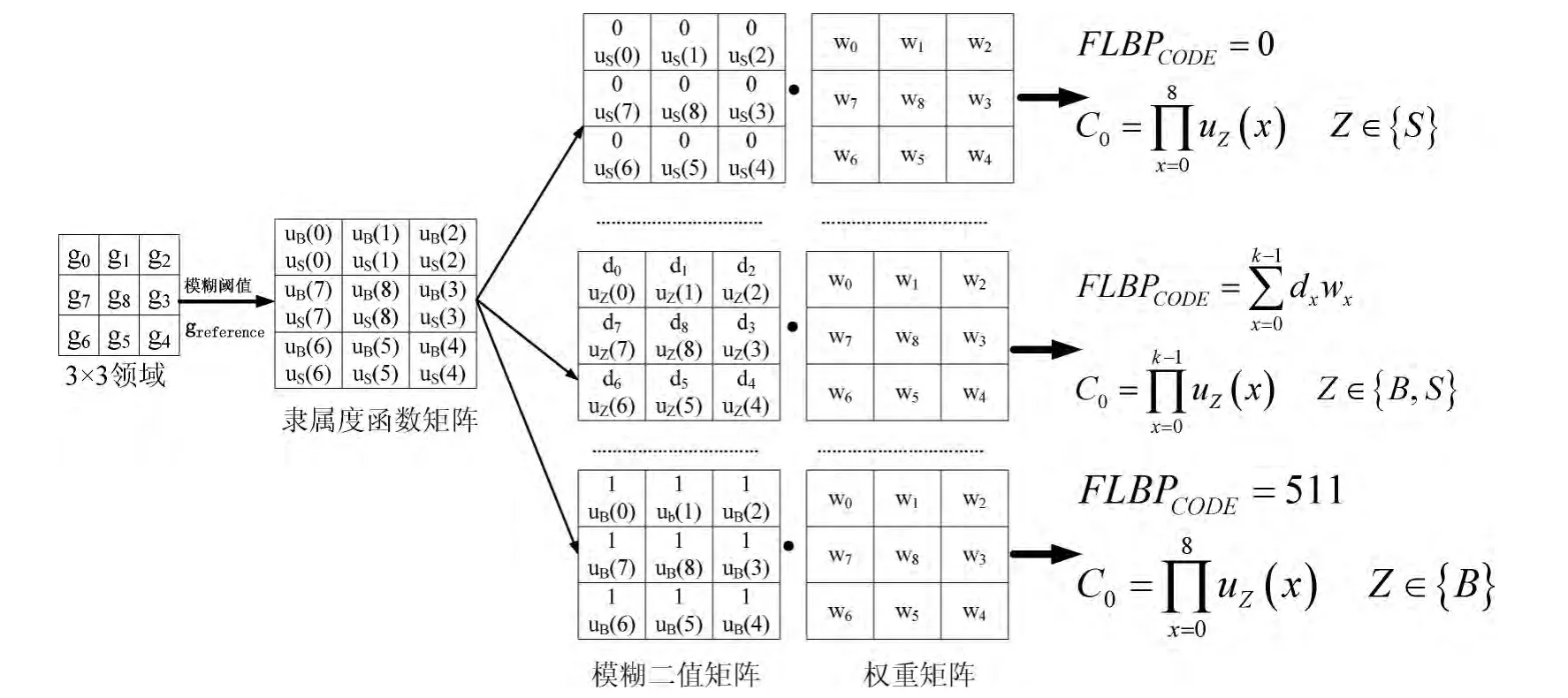
图4 本文设计的模糊局部二值模式算子的计算

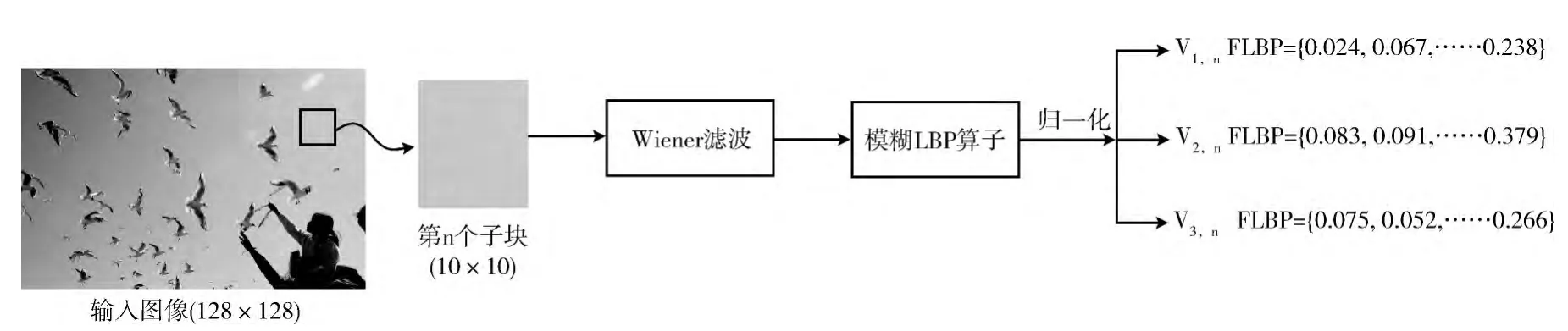
图5 第n个子块的模糊LBP算子特征提取

根据模型 （1）与FLBP算子可知，对于图5中的输入图像，会产生14 161 个重叠块，且每个分块都会有3 个FLBP算子。因此，本文引入字典排序［11］，对这些特征矢量进行排序；并定义3 个特征矩阵：FM1＝Matrix（V1），FM2＝Matrix（V2），FM3＝Matrix（V3），这些矩阵的行与列分别代表分块引擎与特征矢量。也就是通过特征提取，整个图像可以用3个特征矩阵来表示。

1.2 块匹配算法设计

假设相似块产生相似特征，在k维空间内，对于一个由n个特征矢量构成的特征矩阵FM ，有FM ＝［V1，V2，…，Vn］T，Vi∈Rk，i＝1，2…n。为了提高块匹配效率与精度，并克服当前图像伪造检测的块匹配需要预设阈值的难题，本文引入字典排序与K－d树，定义识别多数规则，设计了新的块匹配算法：

步骤1 给定输入图像，再次引入字典排序，对特征矩阵FM1，FM2，FM3进行处理。对于每个特征矩阵的特征矢量，确定出与其对应的欧式距离最小的匹配矢量。欧式距离计算模型为［12］

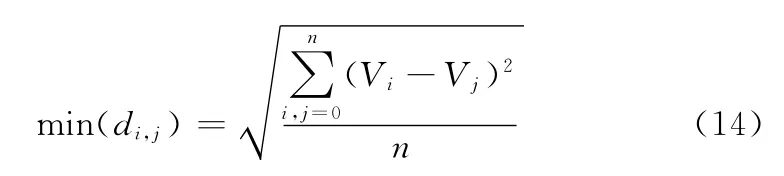
式中：Vi，Vj——相应矩阵中的特征矢量；n——特征矢量的维数。

对于输入图像的第n 个分块，其在特征矩阵FM1，FM2，FM3中 的 特 征 矢 量 分 别 为V1，n（i1），V2，n（i2），V3，n（i3），i1，i2，i3代表FM1，FM2，FM3中行的位置，则第n个分块的中心坐标为（xn，yn）。首先，确定特征矩阵FM1中的第n个分块对应的相似块。为了使用K－d树搜索机制来提高搜 索 效 率［13］，令FM1（i1）＝V1，n（i1）。将V1，n（i1）视为一个model，以及特征矢量S 的集合视为一个参考Reference，即S ＝Reference。S的计算模型为

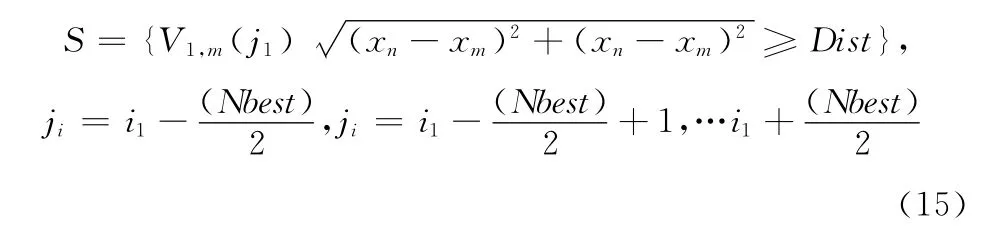
式中：m——图像重叠块的数量，对于图5，m ＝1，2…，14161。

随后，使用函数CV ＝K－d（model，reference），利用Reference 中的特征矢量建立K－d树，并在model 中进行查询，在参考Reference 中，搜索出与model中的特征矢量最近 的 矢 量CV（Close Vector），也 就 是Vi，Vj满 足 模 型（14）。例如，对于特征矩阵FM1，每对匹配块都会存入一个相应矩阵CM1中，包含14161行和2列。同样地，对于FM2，FM3，也产生相应矩阵CM2，CM3。

步骤2 在每个相应矩阵CM1，CM2，…，CMn中，任何一个重叠块都是与另外一个分块进行匹配。为了鉴定出真实的复制移动伪造分块，本文定义了识别多数规则：如果至少有两个对应矩阵CMi，CMj（i≠j）产生了相同的结果，则这些重叠块被视为伪造分块。例如，对于图5 中的第n个分块，3个对应矩阵CM1，CM2，CM3分别为

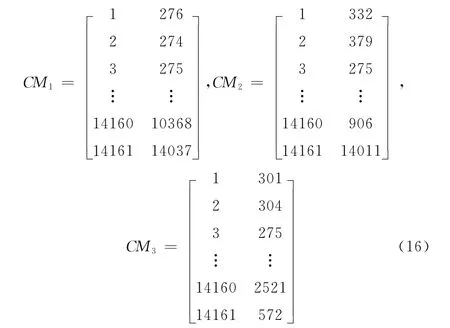
在CM1，CM2，CM3中，第一个分块 “n＝1”分别与块276、332以及301对应，由于在这些矩阵中，其对应的值都不相等，故第一个分块为真实区域；第3个分块 “n＝3”分别与块275、275 以及275 对应，在3 个矩阵中，CM1，CM2，CM3对应的值都相等，故第3、第275个分块被视为复制移动分块。

利用本文设计的块匹配算法，处理所有的对应矩阵CM1，CM2，…，CMn，将结果存入相似块矩阵中，检测出真实的伪造分块。以图6 （b）为例，利用本文设计的块匹配算法对伪造区域进行检测，如图6 （c）所示。从图6中可知，虽然利用本文匹配算法能够检测出伪造目标，但是由于这些块的纹理相似度很高，使得匹配结果存在很多的图像特征误配现象，如图6 （c）所示。

图6 重叠块匹配结果

1.3 随机样本一致策略

为了消除块匹配期间存在的特征误配，本文引入随机样本一致策略来解决。随机样本一致策略［14］是根据一组包含异常数据的样本数据集，通过迭代，得到数据的数学模型参数，继而产生有效样本数据的非确定性的算法。该策略一般由两个步骤构成：假设与验证。从数据集中随机择取出用于确定模型参数所需的最少数量的样本点。每个点的择取概率相同，且仅使用这些点来计算假设模型的参数；在数据集中统计满足假设模型参数的样本的数量，最多样本符合的参数就被当作成最终模型的参数值［6］。满足假设模型所需的点被视为内点 （Inliers）；反之，为外点 （Outliers）。随机样本一致策略的核心为：将数据分割成Inliers与Outliers；只利用Inliers来进行模型的参数的计算，通过迭代假设模型参数，提高算法精度，有效去除块匹配算法中存在的特征误配，获取更鲁棒的匹配结果。利用随机样本一致策略消除特征误配的详细算法步骤，见文献 ［6］。

为消除图6 （c）中误配，利用随机样本一致策略来鉴定相似块矩阵中的匹配块之间的内点Inliers并消除误配Outliers。这些相似块矩阵中的数据点经过了旋转、缩放以及平移处理。即使出现较多误配点对，随机样本一致策略仍然可以精确估算模型参数。给定两个相应的匹配块中心坐标（x，y）T和（x′，y′）T，则旋转、缩放以及平移的函数形式为

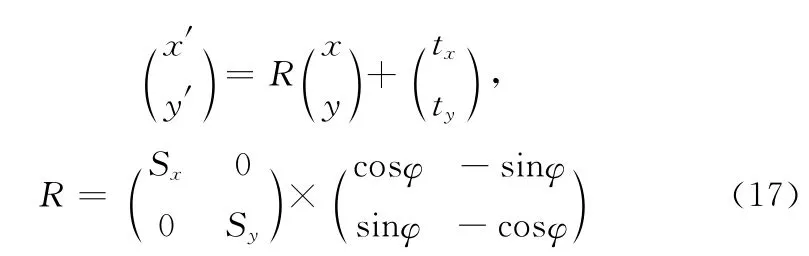
利用随机样本一致策略对其进行处理图6 （c），结果见图6 （d）。从图6 （d）中可知，经过随机样本一致策略处理后，显著消除了图6 （c）中的匹配点对的误配现象，继而有效提高了算法的检测精度。

2 仿真结果及分析

本文借助文献 ［15］中的数据集进行测试。仿真环境为：采用DELL，2.5GHz 双核CPU，500GB 硬 盘，4GB的内存，运行条件为Windows Xp。为了体现本文算法的优越性能，采用当前移动复制伪造检测性能的算法作为对照组：文献 ［6］的基于随机样本一致策略技术；文献 ［16］的基于LBP 技术，分别记为A、B 算法。取Space ＝1，重叠块尺寸B×B ＝10×10，Nbest＝50。

2.1 算法鲁棒性测试

本文测试了4 种 伪 造 形 式：缩 放S （Sx＝0.3，Sy＝0.3）、旋转R（φ＝86°）、高斯噪声N （5dWB）及3种组合 （缩放＋旋转＋噪声）SRN，分别如图7 （b）、图8（b）、图9 （b）以及图10 （b）所示。利用本文算法与对照组对其进行检测，结果如图7～图10 所示。从图中可知，对于这4种伪造形式，本文算法的视觉检测质量最好，即使在3种组合SRN 伪造形式下，仍然能够精确检测出篡改区域，具有更强的鲁棒性能，并显著降低了误匹配点对数量，如图7 （c）～图10 （c）所示；而对照组算法的鲁棒性不佳，A 算法对旋转、噪声具有较强的鲁棒性，但是难以检测缩放、组合伪造SRN 等处理，如图7 （e）、图10 （e）所示；B算法能够较好地检测旋转、缩放等伪造，但是难以检测噪声、组合伪造SRN 等形式的篡改，且存在明显的特征点对误配，如图9 （d）、图10 （d）所示。

2.2 算法检测精度分析

根据图7的测试结果，由于A、B算法在SRN 组合伪造形式下，无法检测出伪造区域。故为了节省实验成本，本文只测试不同的缩放S、旋转R 以及高斯噪声N 等3种篡改方式下的检测结果。本文使用召回率 （Recall）和精度 （Precise）准则［17］来量化这些算法的检测性能

式中：TP——篡改区域被正确检测的像素数量；FP——误判为篡改的像素数量；FN——篡改像素漏检的像素数量。

图7 缩放伪造下，不同算法的检测结果

图8 旋转伪造下，不同算法的检测结果

图9 噪声伪造下，不同算法的检测结果

图10 3种组合SRN 伪造下，不同算法的检测结果

利用3种算法测试缩放S、旋转R、高斯噪声N 以及3种组合 （缩放＋旋转＋噪声）SRN 下的Recall 与Precise，结果如图11所示。从图11中可知，对于任意角度的旋转操作，本文算法的Recall与Precise 始终保持较高水平，其召回率Recall以及精度Precise 均维持90%以上，而A、B算法随着旋转角度的增大，其Recall 与Precise 都在下降，如图11 （c）、图11 （d）所示；随着缩放尺度增大，3种算法的Recall与Precise 都在下降，但是本文算法的下降幅度很小，而A 算法在缩放因子不超过1.3时，也具有较高的检测精度，但是超过1.3 时，其检测效果较差，另外，B算法难以检测缩放篡改，其检测精度很低，如图11 （a）、图11 （b）所示；在任意高斯噪声下，只有本文算法能够精确检测出伪造像素，当噪声功率超过5dWB 时，A、B 算法的Recall与Precise 均为0，如图11 （e）、图11 （f）所示。原因是本文算法设计了模糊LBP 算子，利用模糊阈值提取特征，避免了硬阈值参数对算法精度的影响，且定义了识别多数规则完成块匹配，利用随机样本一致策略消除特征点对误配，本文算法充分结合了LBP算子与随机样本一致策略的优势，继而使得算法的检测精度较高；而A 算法是利用传统的LBP 算子，通过硬阈值参数进行特征提取，使其算法精度严重依赖于硬阈值的择取，且存在较多的特征点对误配，导致其检测精度不佳；B 算法虽然利用了随机样本一致策略，但是该技术仍然需要硬阈值来提取特征，使其精度受限。

3 结束语

为了提高伪造检测算法的鲁棒性，有效检测旋转、缩放以及噪声等形式的篡改，并使得算法精度不受阈值参数的影响，本文提出了随机样本一致策略耦合局部二值模式算子的图像伪造检测算法。基于局部二值模式，引入模糊逻辑，设计了模糊二值模式算子，增强算子的识别能力，提取图像特征；嵌入K－d树与字典排序法，定义识别多数规则，设计高效块匹配算法，精确检测伪造区域分块；利用随机样本一致策略，确定几何变换参数，并消除图像分块误配现象，显著提高算法精度。仿真结果显示本文算法具有更高的检测测精度以及更强的鲁棒性。

图11 不同算法的伪造检测精度测试结果

［1］GK Birajdar，VH Mankar.Digital image forgery detection using passive techniques：A survey ［J］.Digital Investigation，2013，10 （3）：226－245.

［2］KANG Xiaobing，WEI Shengmin.Adaptive threshold－based detection algorithm for image copy－forgery ［J］.Computer Science，2011，38 （3）：295－299 （in Chinese）. ［康晓兵，魏生民.一种基于自适应阈值的图像伪造检测算法 ［J］.计算机科学，2011，38 （3）：295－299.］

［3］Ansari MD，Ghrera SP，Tyagi V.pixel－based image forgery detection：A review ［J］.IETE Journal of Education，2014，55 （1）：40－46.

［4］Hashmi MF，Hambarde AR.Copy move forgery detection using DWT and SIFT features［J］.Intelligent Systems Design and Applications，2013，34 （10）：188－193.

［5］Irene Amerini，Lamberto Ballan.Copy－move forgery detection and localization by means of robust clustering with J－Linkage［J］.Signal Processing：Image Communication，2013，28（6）：659－669.

［6］WANG Renhua，HUO Hongtao，JIANG Min.Application research of RANSAC algorithm on copy－move forgery detection［J］.Journal of Computer Application，2014，31 （7）：2209－2212 （in Chinese）.［王任华，霍宏涛，蒋敏.RANSAC算法在同图复制鉴定中的应用研究 ［J］.计算机应用研究，2014，31 （7）：2209－2212.］

［7］OU Hongyu，CHEN Xi，SONG Yanhui.Detection of image duplication forgery based on local binary pattern ［J］.Computer Application and Software，2013，30 （9）：170－173 （in Chinese）.［欧红玉，陈曦，宋燕辉.基于LBP的图像复制篡改检测 ［J］.计算机应用与软件，2013，30 （9）：170－173.］

［8］LIU Zhe，CHEN Lu，YANG Jing.An image reconstruction algorithm using patch－based locally optimal wiener filter ［J］.Journal of Electronic ＆ Information Technology，2014，36（11）：2556－2562 （in Chinese）.［刘哲，陈路，杨静.一种基于块局部最优维纳滤波的图像重构算法 ［J］.电子与信息学报，2014，36 （11）：2556－2562.］

［9］Zhou SR，Yin JP，Zhang JM.Local binary pattern （LBP）and local phase quantization（LBQ）based on Gabor filter for face representation ［J］. Neurocomputing，2014，116 （20）：260－264.

［10］Yerushalmy I，Hel－Or H.Digital image forgery detection based on lens and sensor aberration ［J］.International Journal of Computer Vision，2011，92 （1）：71－77.

［11］Zimba M，Xingming S.DWT－PCA （EVD）based copy－move image forgery detection［J］.International Journal of Digital Content Technology and its Applications，2011，5 （1）：251－258.

［12］OU Jiajia，CAI Biye，XIONG Bing，et al.Detection of image region duplication forgery based on LBP ［J］.Computer Engineering，2012，38 （16）：226－229 （in Chinese）. ［欧佳佳，蔡碧野，熊兵，等.基于LBP 的图像区域复制篡改检测［J］.计算机工程，2012，38 （16）：226－229.］

［13］Duch A，Jiménez RM，Martínez C.Selection by rank in Kdimensional binary search trees ［J］.Random Structures ＆Algorithms，2012，45 （1）：14－37.

［14］Misra I，Moorthi SM，Dhar D.An automatic satellite image registration technique based on Harris corner detection and random sample consensus（RANSAC）outlier rejection model［J］.Recent Advances in Informatio，2012，15 （7）：68－73.

［15］Muhammad G，Hussain M，Bebis G.Passive copy move image forgery detection using undecimated dyadic wavelet transform ［J］.Digital Investigation，2012，9 （1）：49－57.

［16］Li L，Li S，Zhu H，et al.An efficient scheme for detecting copy－move forged images by local binary patterns［J］.Journal of Information Hiding and Multimedia Signal Processing，2013，4 （1）：46－56.

［17］Ryu SJ，Lee MJ，Lee HK.Detection of copy－rotate－move forgery using zernike moments ［J］.Information Hiding，2010，12 （5）：51－65.